Branched Coverings and Embedded Surfaces in Four-manifolds
LIU XI-MIN AND WU YU-LAI
(School of Mathematical Sciences,Dalian University of Technology,Dalian,Liaoning,116024)
Communicated by Lei Feng-chun
Branched Coverings and Embedded Surfaces in Four-manifolds
LIU XI-MIN AND WU YU-LAI
(School of Mathematical Sciences,Dalian University of Technology,Dalian,Liaoning,116024)
Communicated by Lei Feng-chun
In this paper,we get a lower bound on the genera of surfaces representing certain divisible classes in some 4-manifold X with H1(X;Z)finite.
embedded surface,4-manifold,genus
1 Introduction
One of the outstanding problems in four-dimensional topology is to find the minimal genus of an oriented smoothly embedded surface representing a given homology class in a smooth 4-manifold.There are a lot of results on this question in the literature.They can be divided into two classes,those proved by classical topological methods and those proved by methods of gauge theory.On the classical side,a major step forward was made by Rokhlin[1],Hsiang and Szczarba[2]who introduced branched covers to study this problem for divisible homology classes.
The applications of gauge theory to this problem were initially concerned with the representability of homology classes by spheres(see the Lawson's survey article[3]).They usually relied on Donaldson's early theorem(see[4])on four-manifolds with b+2≤2.Substantial progress was made recently by Kronheimer and Mrowka[5–6]who developed gauge theory for singular connection with non-trivial holonomy around a loop linking an embedded surface Σ.They used this to prove that if X has non-trivial Donaldson invariants(see[7]),then the genus g(Σ)of Σ satisfiesexcept that Σ is an inessential sphere or a sphere of self-intersection-1.Later Kotschick and Matiˊc[8]combined the classical method using branched covers with gauge theoretic arguments to prove some results about the lower bound on the genera of surfaces representing certain divisible classes in 4-manifolds.
These results were obtained under the assumption that the 4-manifold is simply connected.In this paper,we discuss this problem for 4-manifold X with H1(X;Z)finite.Here we do not use Donaldson theory,but use some results obtained by using Seiberg-Witten theory.Together with the classical method for branched coverings,we get some results about the lower bound on the genera of surfaces representing certain divisible classes in some 4-manifold X with H1(X;Z)finite.
2 Branched Coverings and Preliminary Results
Let X be a closed 4-manifold with H1(X;Z)finite,B?X be a connected closed oriented surface representing a homology class v∈H2(X;Z),and g be the genus of B.Split
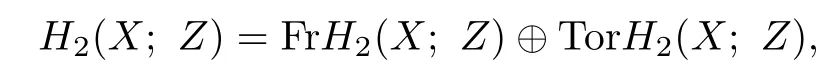
and denote by b2the second Betti number of X.Suppose that p is a prime such that p devides v|FrH2(X;Z).Let T?X be a tubular neighborhood of the branch locus B,and W=closur(X-T).
Lemma 2.1H1(W)is a finite group,and it contains a subgroup G~=Zpr.
Proof.By excision and duality,we have
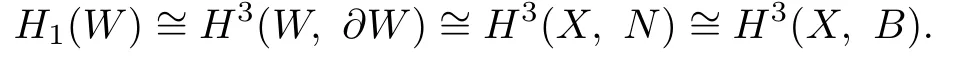
The exact sequence of the pair(X,B)gives

and since H2(B)~=Z,i*is determined by
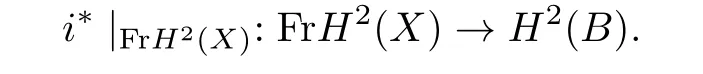
Let
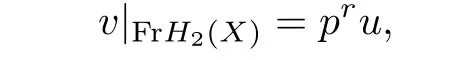
and choose a base v1,···,vb2for FrH2(X)with v1=u.Let φ1,···,φb2be the dual base for FrH2(X),andμ∈H2(B)dual to[B]∈H2(B).Since i*|FrH2(X)=Hom(i*,1),we have
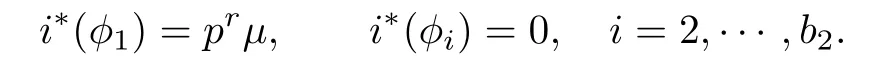
Let G be the subgroup of H3(X,B)generated by σ*μ.Then G~=Zprand G?kerj*. Since H3(X)~=H1(X)is a finite group,H3(X,B)is a f i nite group.This completes the proof of Lemma 2.1.
Now let V→W be the unramified covering corresponding to the homomorphism
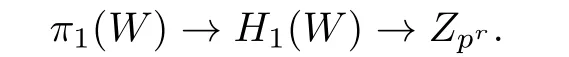
Since the normal bundle NBhas degree[B]2,and pr|[B]2,there is a pr-fold cover of NBby the line bundle of degree[B]2/prgiven by(w,x)(wpr,x).Using the identification of T with NBwe get a prcover→T ramified along B.It is easy to see that we can constructed a pr-fold branched covering Y→X with Y=V∪,branched along B?X.
Proposition 2.1If pris the maximal power of p dividing v|FrH(X,Z),then
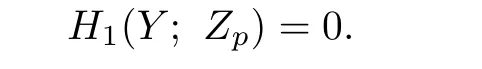
Proof.Let M→N be the standard ramified covering.Then we have
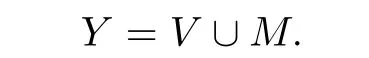
The Mayer-Vietoris sequence for this decomposition gives
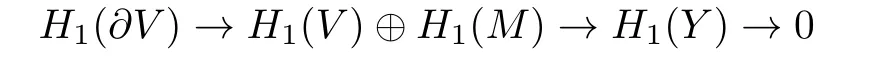
for homology with arbitrary coefficients.
Because
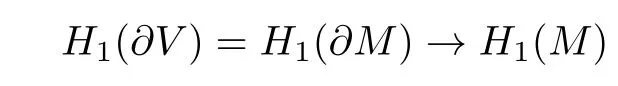
is surjective,if we want to get
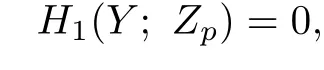
it is only to prove that
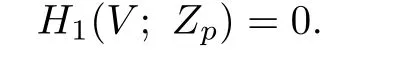
Let
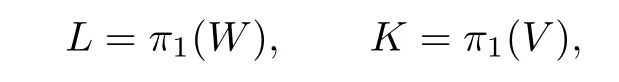
L′and K′be commutator subgroups of L and K,respectively.By Lemma 4.1 of[2], K/K′=H1(V)is a finite group,and by Lemma 2.2 of[8],p does not divide the order of H1(V).So
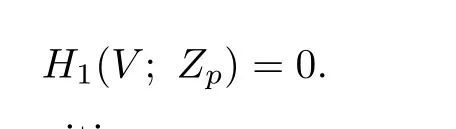
This completes the proof of the proposition.
Remark 2.1From[8]we know that the assumption of maximality in Proposition 2.1 can be dropped.
Lemma 2.2(a)If v2/=0,then rankH1(?W)=rankH2(?W)=2g.
(b)If v2=0,then rankH1(?W)=rankH2(?W)=2g+1.
Proof.(b)is trivial.To prove(a),we consider the Gysin sequence for the S1-bundle?N→B:
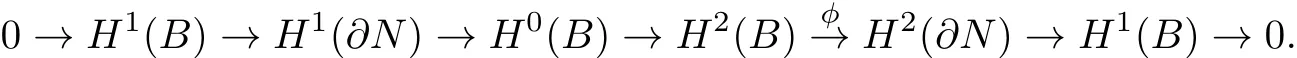
Since φ is the multiplication by the Euler class v2·μof the bundle?N→B,it is an isomorphism and the result follows.
Lemma 2.3If H1(X,Zp)is cyclic for a prime p,then rankH2(V)=pr(2g+b2)-1. Proof.By Lemma 4.4 of[9]we have
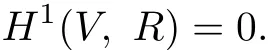
It follows easily that
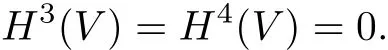
By excision and duality we have
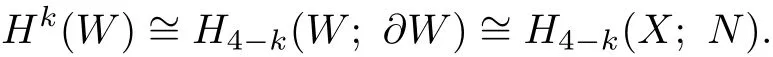
Using exact sequence for the pair(X,N),we can compute the Euler characteristic χ(W) of W,which is 2g+b2.So the Euler characteristic χ(V)of V is pr(2g+b2).Thus
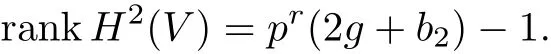
Proposition 2.2rankH2(Y)=2(pr-1)g+prb2.
Proof.Since
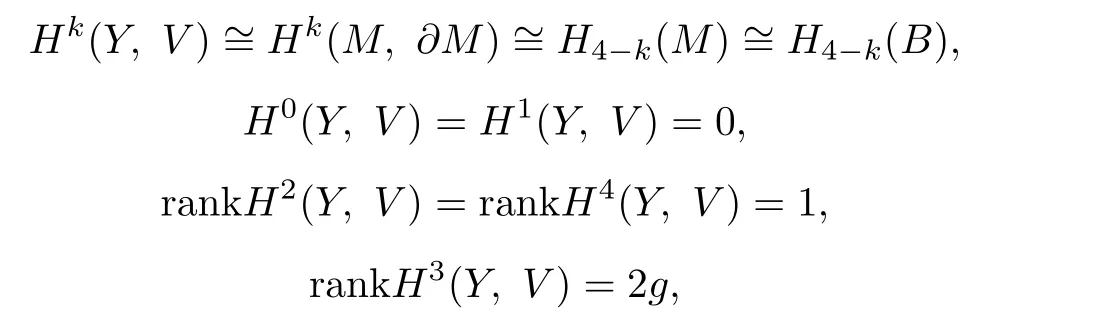
by the cohomology sequence of pair(Y,V)and Lemma 2.3,we have
Then,from exact sequence

we get
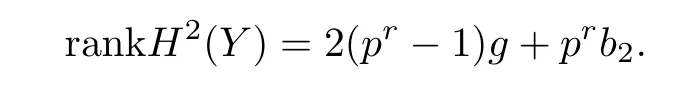
Proposition 2.3where σ(Y)and σ(X)denote the signature of Y and X,respectively.
Proof.It can be verified easily from Lemma 2.1 of[9].
Let X be a smooth,closed,connected spin 4-manifold.Denote by b2(X)the second Betti number and by σ(X)the signature of X.The following inequality is the well known-conjecture:

Suppose that σ(X)≤0 in the following.Let
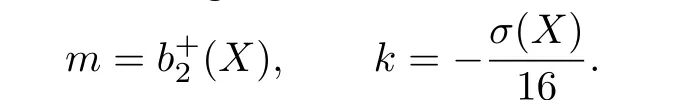
Then the inequality(2.1)is equivalent to 3k≤m.
In[10],by using the finite dimensional approximation of the monopole equations,Furuta proved the following-theorem.
Theorem 2.1[10]Let X be a smooth spin 4-manifold with b1(X)=0 with non-positive signature.and.Then 2k+1≤m if m/=0.
A Z/2p-action is called a spin action if the generator of the action τ:X→X lifts to an action?τ:Pspin→Pspinof the spin bundle Pspin.Such an action is of even type if?τ has order 2pand is of odd type if?τ has order 2p+1.
In[11],Bryan(see also[12])used Furuta's technique of finite dimensional approximation and the equivariant K-theory to improve the above bound by p under the assumption that X has a spin odd type Z/2p-action satisfying some non-degeneracy conditions.More precisely, he proved
Theorem 2.2[11]Let X be a smooth,closed,connected spin 4-manifold with b1(X)=0. Assume that τ:X→X generates a spin smooth Z/2p-action of odd type.Let Xidenote the quotient of X by Z/2i?Z/2p.Then
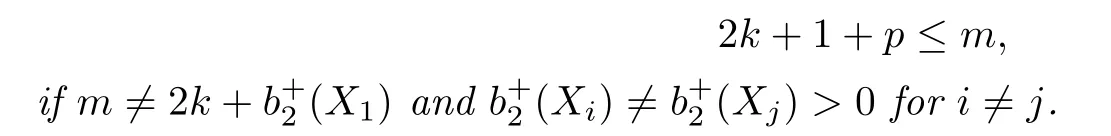
Let Σ→X be an embedding of an oriented surface of genus g=g(Σ)into an oriented smooth 4-manifold X with H1(X;Z)finite.Assume that the class[Σ]∈H2(X;Z)is divisible by a prime power pr.So we can consider the ramified cover f:Y→X with covering group Zpr.
The 4-manifold Y admits a spin structure if and only if ω2(Y)=0.Brand[13]gave a general formula for the characteristic numbers of the general branched cover.Let
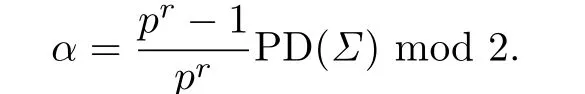
In our case Brand's formula becomes
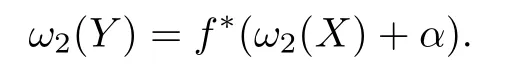
Note that if pris odd then α=0.To guarantee that Y is spin we always make the following assumption:If pris odd we assume that X is spin;if pris even,we assume that PD(Σ)/pris characteristic.
The following lemma tells us when the covering transformation is a spin action of odd type.
Lemma 2.4If H1(Y;Z2)is trivial,then the action of the covering transformation is a spin action of odd type.
Proof.For a given Riemannian metric on Y,let PSO(4)be the frame bundle of the tangent bundle of Y.Then a spin structure on Y is just a cohomology class in H1(PSO(4),Z2) whose restriction to H1(SO(4),Z2)≡Z2is the generator.Since Y is spin,we have the following exact sequence associated to the frame bundle:
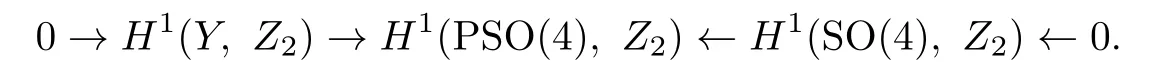
So H1(PSO(4),Z2)is isomorphic to Z2,and thus there is a unique spin structure Pspin→PSO(4).Since any diffeomorphism f:Y→Y induces an isomorphism of H1(PSO(4),Z2), f preserves the unique spin structure and is a spin action.The action of the covering transformation is of odd type because the fixed point set is two dimensional,so the lemma is proved.
3 Main Results
Combining the results of Section 2,we prove some results about the lower bound on the genera of embedded surfaces representing certain homology classes in a smooth 4-manifold X with H1(X;Z)finite.
Theorem 3.1Let X be a smooth oriented 4-manifold with H1(X,Z)finite,and Σ?X be a connected oriented smoothly embedded surface representing a non-zero homology class [Σ]∈H2(X,Z).Assume that[Σ]∈H2(X,Z)is divisible by 2r,1 2r[Σ]is Poincarˊe dual to a lift of ω2(X)to integral coefficients,and b+2(X)/=0.Then

Proof.Let π:Y→X be the 2r-fold cover branched along Σ.Then

where PD(α)denotes the Poincarˊe dual of α.Thus Y is a spin manifold.By Propositions 2.2 and 2.3 we have
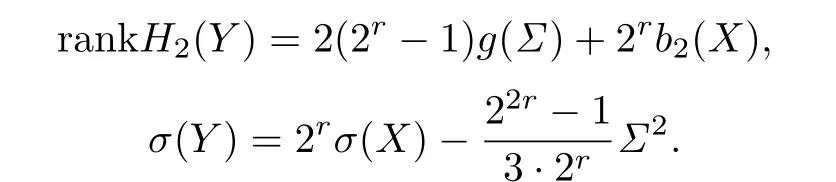
By Proposition 2.1 we have
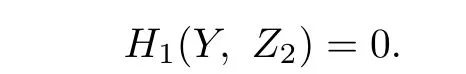
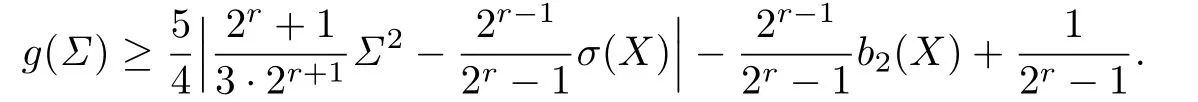
This completes the proof of Theorem 3.1.
Theorem 3.2Let Σ→X be an embedding of an oriented surface of genus g=g(Σ) into an oriented,smooth 4-manifold X with H1(X;Z)f i nite.Assume that the class[Σ]∈H2(X,Z)is divisible by a prime power 2rand≡ω2(X)mod 2.Suppose that>1 andfor 1=1,···,r-1.Then
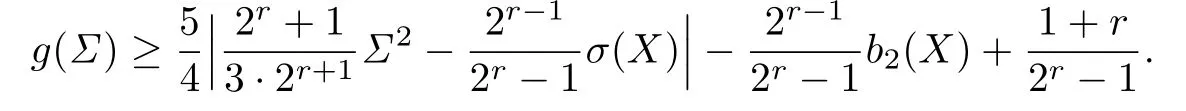
Proof.Let Y→X be the 2r-th branched cover,and Yithe 2r-ibranched cover.Then

and Yiis the quotient of X by.Let
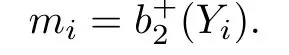
Then we have

Note that

The inequality of the theorem is equivalent to Theorem 2.2,that is,

So the only way the theorem can fail is if
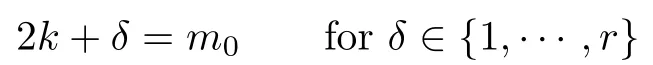
and
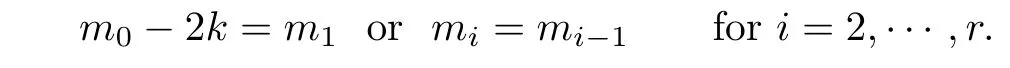
The hypothesis
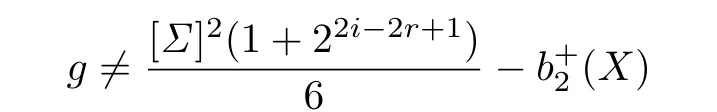
is equivalent to

so we know
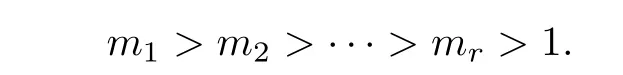
This implies that

So we cannot have
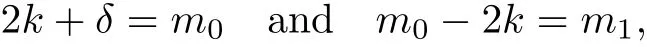
since that would imply δ>r.That is a contradiction.So we finished the proof of Theorem 3.2.
[1]Rokhlin V A.Two-dimensional submanifold of four-dimensional manifolds.Funct.Anal.Appl., 1971,6:29–48.
[2]Hsiang W C,Szczarba R H.On embedding surfaces in four-manifolds.Proc.Sympos.Pure Math.,1971,22:97–103.
[3]Lawson T.Smooth embeddings of 2-spheres in 4-manifolds.Exposition Math.,1992,10:289–309.
[4]Donaldson S K.The orientation of Yang-Mills moduli spaces and 4-manifold topology.J. differential Geom.,1987,26:397–428.
[5]Kronheimer P B,Mrowka T S.Gauge theory for embedded surfaces I.Topology,1993,32: 773–826.
[6]Kronheimer P B,Mrowka T S.Gauge theory for embedded surfaces II.Topology,1995,34: 37–97.
[7]Donaldson S K.Polynomial invariants for smooth four-manifold.Topology,1990,29:257–315.
[8]Kotschick D,Matiˊc G.Embedded surfaces in four-manifolds,branched covers,and SO(3)-invariants.Math.Proc.Cambridge Philos.Soc.,1995,117:275–286.
[9]Casson A J,Gordon C McA.On slice knots in dimension three.Proc.Sympos.Pure Math., 1978,32:39–53.
[10]Furuta M.Monopole equation and-conjecture.Math.Res.Letter,2001,8:279–291.
[11]Bryan J.Seiberg-Witten theory and Z/2pactions on spin 4-manifolds.Math.Res.Lett.,1998, 5:165–183.
[12]Fang F.Smooth group actions on 4-manifolds and Seiberg-Witten theory.Differential.Geom. Appl.,2001,14:1–14.
[13]Brand N.Necessary conditions for the existence of branched coverings.Invent.Math.,1979, 54:1–10.
57R40,57R95,57N13
A
1674-5647(2013)04-0370-07
Received date:Oct.2,2011.
The NSF(10931005)of China.E-mail address:ximinliu@dlut.edu.cn(Liu X M).
 Communications in Mathematical Research2013年4期
Communications in Mathematical Research2013年4期
- Communications in Mathematical Research的其它文章
- Invariants for Automorphisms of the Underlying Algebras Relative to Lie Algebras of Cartan Type
- COMMUNICATIONS IN MATHEMATICAL RESEARCH
- Annulus and Disk Complex Is Contractible and Quasi-convex
- An Extension of Chebyshev's Maximum Principle to Several Variables
- A Class of Regular Simple ω2-semigroups-II
- On Results the Growth of Meromorphic Solutions of Algebraic differential Equations
