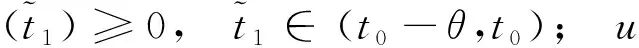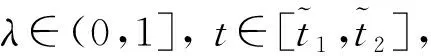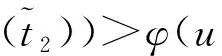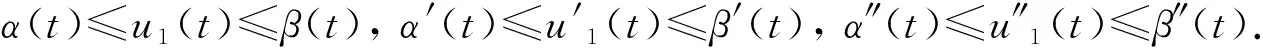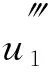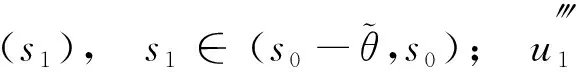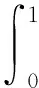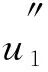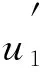具積分邊值條件四階微分方程解的存在性
宋文晶,高文杰
(1.吉林財經(jīng)大學(xué) 應(yīng)用數(shù)學(xué)學(xué)院,長春 130117;2.吉林大學(xué) 數(shù)學(xué)研究所,長春 130012)
0 引言與預(yù)備知識
積分邊值問題源于熱傳導(dǎo)問題[1]、 半導(dǎo)體問題[2]及水動力學(xué)問題[3],目前已有許多研究結(jié)果[4-10].本文基于文獻(xiàn)[4-5],研究下列具有積分邊值條件的四階常微分方程解的存在性:
(1)
其中:f: [0,1]×4→和hi:→(i=1,2)是連續(xù)函數(shù);k1,k2≥0;φ(u)是嚴(yán)格增的連續(xù)函數(shù),且φ(0)=0,φ()=,=(-∞,+∞).
定義1設(shè)函數(shù)α,β∈C3([0,1]),φ(α?(t)),φ(β?(t))∈C1([0,1]),滿足α″(t)≤β″(t),?t∈[0,1],若下列條件成立,則稱β(t),α(t)為問題(1)的一對上下解:
1) (φ(α?(t)))′≥-f(t,α(t),α′(t),α″(t),α?(t)),(φ(β?(t)))′≤-f(t,β(t),β′(t),β″(t),β?(t));

3)α′(0)-β′(0)≤min{β(0)-β(1),α(1)-α(0),0}.
定義2令集合D∶={(t,x0,x1,x2,x3)∈[0,1]×4:γi(t)≤xi(t)≤Γi(t),i=0,1,2},其中Γi(t),γi(t): [0,1]→(i=0,1,2)連續(xù),且γi(t)≤Γi(t),i=0,1,2,t∈[0,1].若存在一個正的連續(xù)函數(shù)Φ: [0,+∞)→[a,+∞),a>0及參數(shù)p>1,使得下式成立,則稱連續(xù)函數(shù)f: [0,1]×4→在D上滿足Nagumo條件:
其中φ-1是φ的逆函數(shù).記ν∶=max{|Γ2(1)-γ2(0)|,|Γ2(0)-γ2(1)|}.
引理1設(shè)f: [0,1]×4→是連續(xù)函數(shù),在D上滿足Nagumo條件,則存在N>0(僅依賴Γ2,γ2和Φ),使得滿足γi(t)≤u(i)(t)≤Γi(t)(i=0,1,2)的問題(1)的每個解u(t),都有‖u?‖∞≤N.
證明: 考慮修正問題:
(φ(u?(t)))′+f*(t,u(t),u′(t),u″(t),u?(t))=0, 0 其中 (4) 由中值定理知,存在一點(diǎn)t0∈(0,1),使得u?(t0)=u″(1)-u″(0),從而有 -N<-ν≤γ2(1)-Γ2(0)≤u?(t0)≤Γ2(1)-γ2(0)≤ν 記v0=|u?(t0)|. 假設(shè)在區(qū)間[0,1]上存在一點(diǎn),使得u?>N或u?<-N,則由u?的連續(xù)性知,存在區(qū)間[t1,t2]?[0,1],且滿足下列情形之一: 1)u?(t1)=v0,u?(t2)=N,v0≤u?(t)≤N,?t∈(t1,t2); 2)u?(t1)=N,u?(t2)=v0,v0≤u?(t)≤N,?t∈(t1,t2); 3)u?(t1)=-v0,u?(t2)=-N,-N≤u?(t)≤-v0,?t∈(t1,t2); 4)u?(t1)=-N,u?(t2)=-v0,-N≤u?(t)≤-v0,?t∈(t1,t2). 假設(shè)1)成立.因?yàn)閠∈(t1,t2),-N≤v0≤u?(t)≤N,所以有 (φ(u?(t)))′=-f*(t,u(t),u′(t),u″(t),u?(t))=-f(t,u(t),u′(t),u″(t),u?(t)),t∈(t1,t2). 由Nagumo條件得, |(φ(u?(t)))′|=|f(t,u(t),u′(t),u″(t),u?(t))|≤Φ(|u?(t)|),t∈(t1,t2), 于是有 與式(4)矛盾.類似可證明其余3種情況.證畢. 引理2邊值問題: (5) 僅有平凡解. 證明略. 假設(shè)條件如下: (H1)β(t),α(t)是問題(1)的一對上下解; (H2)f∈C([0,1]×4,),且在D∶=[0,1]×[α(t),β(t)]×[α′(t),β′(t)]×[α″(t),β″(t)]×上滿足Nagumo條件,當(dāng)(t,x2,x3)∈[0,1]×2,(α(t),α′(t))≤(x0,x1)≤(β(t),β′(t))時,f滿足 f(t,α(t),α′(t),x2,x3)≤f(t,x0,x1,x2,x3)≤f(t,β(t),β′(t),x2,x3), 其中(x0,x1)≤(y0,y1),即x0≤y0,x1≤y1;hi:→(i=1,2)是連續(xù)的,且(u)≥0(i=1,2); (H3)φ是連續(xù)的且嚴(yán)格遞增,φ(0)=0,φ()=. 定理1假設(shè)條件(H1)~(H3)成立,則問題(1)至少存在一個解u(t),且對任意的t∈[0,1],有α(t)≤u(t)≤β(t),α′(t)≤u′(t)≤β′(t),α″(t)≤u″(t)≤β″(t),|u?(t)|≤N,這里N是僅依賴于α,β和Φ的常數(shù). 證明: 令δ1,δ2,δ3∈,且δ1≤δ3,定義 對于λ∈[0,1],考慮輔助問題: (6) 其中Φ(|u?(t)|)是Nagumo條件定義的,其邊值為 (7) 選取M1>0,使得對任意的t∈[0,1],下列不等式成立: 1) 證明對λ∈[0,1],問題(6)-(7)的每個解u(t),都滿足|u(t)| 如果λ=0,則由引理2知,結(jié)論顯然成立.下面考慮λ∈(0,1].假設(shè)|u″(t)| (13) ① 若t0∈(0,1),則u?(t0)=0.由f和Φ的連續(xù)性及式(10)可知,存在η>0,使得當(dāng)|y|<η時,有 -f(t,β(t),β′(t),β″(t),y)+[M1-η-β″(t)]Φ(|y|)>0. 由式(13),存在θ∈(0,min{t0,1-t0}),使得 |u?(t)|<η,u″(t)>M1-η>max{0,β″(t)},t∈(t0-θ,t0+θ), ② 若t0=0,則 ?(0+)=u?(0)≤0. 由式(7),(11)可得 矛盾. ③t0=1的情形同②. 因此u″(t) 由邊值條件(7)知,存在一點(diǎn)ξ∈(0,1),使得u′(ξ)=0.經(jīng)積分運(yùn)算得 2) 證明存在M2>0,使得對于問題(6)-(7)的每個解u(t),都有|u?(t)| 如果u(t)是問題(6)-(7)的一個解,則考慮集合 DM1={(t,x0,x1,x2,x3)∈[0,1]×4: -M1≤x0≤M1,-M1≤x1≤M1,-M1≤x2≤M1}. 定義函數(shù)Fλ:DM1→為 由于f在D上滿足Nagumo條件,所以有 此外,有 因此,Fλ在DM1上滿足Nagumo條件,且不依賴于λ∈[0,1].令Γi(t)=M1,γi(t)=-M1,i=0,1,2,由引理1知,存在M2>0,使得|u?(t)| 3) 證明λ=1 時,問題(6)-(7)至少存在一個解u1(t). 定義算子M:C3([0,1])∩domM→C([0,1])×4為 Mu=(Φ(u?(t))′,u(0),u(1),u″(0),u″(1)), Nλ:C3([0,1])→C([0,1])×4為 其中: 由于M-1是緊的,因此考慮全連續(xù)算子Tλ: (C3[0,1],)→(C3[0,1],),Tλ(u)=M-1Nλ(u),集合 ?‖∞ 由引理2知,u=T0(u)僅有平凡解,再由同倫不變性得,d(I-T0,Ω,0)=d(I-T1,Ω,0)=±1.因此,方程u=T1(u)在Ω上至少有一個解u1(t). 4) 證明函數(shù)u1(t)是問題(1)的一個解. (14) 且存在s1,s2,使得 于是,對于t∈[s1,s2],有 但對于t∈[s1,s2],有 矛盾. ② 若s0=0,則 由于 故s0≠0. 由定義1,有 (0), [1] Cannon J R.The Solution of the Heat Equation Subject to the Specification of Energy [J].Quart Appl Math,1963,21(2): 155-160. [2] Ionkin N I.Solution of a Boundary Value Problem in Heat Conduction Theory with Nonlocal Boundary Conditions [J].Differential Equations,1977,13: 294-304. [3] Chegis R Y.Numerical Solution of a Heat Conduction Problem with an Integral Boundary Condition [J].Litovsk Mat Sb,1984,24: 209-215. [4] WANG You-yu,GE Wei-gao.Existence of Solutions for a Third Order Differential Equation with Integral Boundary Conditions [J].Comput Math Appl,2007,53(1): 144-154. [5] WANG You-yu,LIU Guo-feng,HU Yin-ping.Existence and Uniqueness of Solutions for a Second Order Differential Equation with Integral Boundary Conditions [J].Appl Math Comput,2010,216(9): 2718-2727. [6] Boucherif A.Second-Order Boundary Value Problems with Integral Boundary Conditions [J].Nonlinear Anal: Theory,Methods &Applications,2009,70(1): 364-371. [7] Ahmad B,Alsaedi A,Alghamdi B S.Analytic Approximation of Solutions of the Forced Duffing Equation with Integral Boundary Conditions [J].Nonlinear Anal Real World Applications,2008,9(4): 1727-1740. [8] SONG Wen-jing,GAO Wen-jie.Existence of Positive Solutions for a System of Second Order Equations with Integral Boundary Conditions [J].Journal of Jilin University: Science Edition,2011,49(3): 363-368.(宋文晶,高文杰.具積分邊值條件二階微分方程組正解的存在性 [J].吉林大學(xué)學(xué)報: 理學(xué)版,2011,49(3): 363-368.) [9] YANG Zhi-lin.Positive Solutions to a System of Second-Order Nonlocal Boundary Value Problems [J].Nonlinear Anal: Theory,Methods &Applications,2005,62(7): 1251-1265. [10] ZHANG Xing-qiu.Existence and Uniqueness of Positive Solution for Fourth-Order Singular Integral Boundary-Value Problems [J].Acta Mathematicae Applicatae Sinica,2010,33(1): 38-50.(張興秋.奇異四階積分邊值問題正解的存在唯一性 [J].應(yīng)用數(shù)學(xué)學(xué)報,2010,33(1): 38-50.)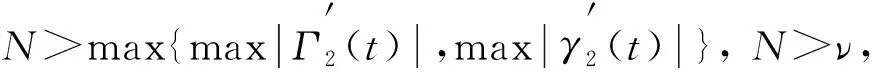
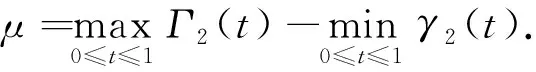
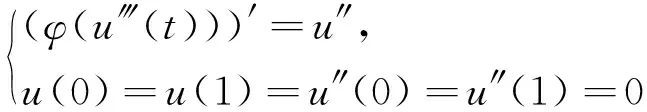
1 主要結(jié)果