鄭喜英, 孔波

(1.黃河科技學(xué)院信息工程學(xué)院,河南 鄭州 450063;2.河南教育學(xué)院數(shù)學(xué)與統(tǒng)計學(xué)院,河南 鄭州 450046)

有限鏈環(huán)上的常循環(huán)碼

鄭喜英1, 孔波2

(1.黃河科技學(xué)院信息工程學(xué)院,河南 鄭州 450063;2.河南教育學(xué)院數(shù)學(xué)與統(tǒng)計學(xué)院,河南 鄭州 450046)

研究了有限鏈環(huán)R上常循環(huán)碼的等價性,根據(jù)等價性給出了R上一些常循環(huán)碼及其對偶碼的結(jié)構(gòu).確定了該環(huán)上長度為ps的所有常循環(huán)碼及其對偶碼的結(jié)構(gòu).

常循環(huán)碼;循環(huán)碼;對偶碼

1 引言

近年,有限環(huán)上的常循環(huán)碼成了很多學(xué)者研究的熱點(diǎn)問題.文獻(xiàn)[1]研究了有限環(huán)(Fp+ uFp+vFp+uvFp)上的(1+λu)-常循環(huán)碼的結(jié)構(gòu),并構(gòu)造了參數(shù)較好的p元線性碼.文獻(xiàn)[2]研究了有限環(huán)(對任意的整數(shù)k≥1)上的循環(huán)碼,定義了一個Gray映射,證明了Rk上循環(huán)碼的Gray像是指數(shù)為2k的二元準(zhǔn)循環(huán)碼.文獻(xiàn)[3]對有限域上的常循環(huán)碼的等價性進(jìn)行了研究,并對其常循環(huán)碼的生成元進(jìn)行了刻畫.文獻(xiàn)[4]研究了有限環(huán)

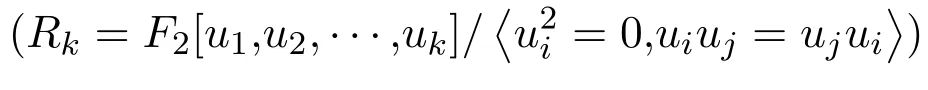
(對任意的整數(shù)k≥1)

上的線性碼,并定義了兩個等價的Gray映射.文獻(xiàn)[5]研究了有限環(huán)上的常循環(huán)自對偶碼的生成多項式.文獻(xiàn)[6]研究了有限環(huán)(F2+uF2+vF2+uvF2)上的常循環(huán)碼及其Gray像的結(jié)構(gòu).文獻(xiàn)[7]研究了環(huán)上的一類常循環(huán)碼及其對偶碼的結(jié)構(gòu).文獻(xiàn)[8]給出了有限鏈環(huán)上循環(huán)碼和負(fù)循環(huán)碼的生成元.文獻(xiàn)[9]研究了環(huán)(Fpm+uFpm)上常循環(huán)碼的等價性,并根據(jù)等價性對該類環(huán)上的常循環(huán)碼進(jìn)行了分類.文獻(xiàn)[10]研究了有限鏈環(huán)上的重根循環(huán)碼的生成多項式.文獻(xiàn)[11]研究了環(huán)(Fpm+uFpm)上常循環(huán)碼的結(jié)構(gòu).本文在文獻(xiàn)[9-11]的基礎(chǔ)上研究了有限鏈環(huán)上的單根及重根常循環(huán)碼及其對偶碼的結(jié)構(gòu)對前面的結(jié)果進(jìn)行了推廣.

2 基礎(chǔ)知識

定義 2.1設(shè)R為一個含單位元1的有限交換環(huán),若1/=0,并且環(huán)R中的全部理想能按照包含關(guān)系構(gòu)成一條鏈,則稱環(huán)R為有限鏈環(huán).

設(shè)R是一個有限鏈環(huán),R的極大理想為I=〈γ〉=γR,其中γ是冪零指數(shù)為e的冪零元, R的所有理想滿足鏈R=γ0R?γ1R?···?γeR.

令F=R/I=R/〈γ〉,則F是特征為素數(shù)p的域,已知存在整數(shù)m使得|F|=pm.令ξ是F的一個本原元,那么F={0,1,ξ,···,ξpm?2}.

由文獻(xiàn)[8]可知R中的每一個元素r都可以唯一的表示為:

環(huán)R上所有的單位元為:

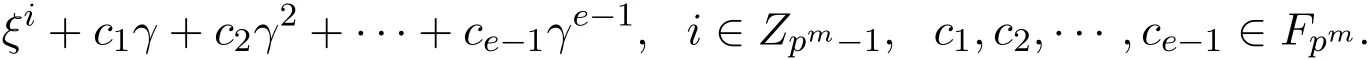
環(huán)R上長為n的線性碼是Rn的一個R-子模.設(shè)v表示Rn上的一個λ-常循環(huán)移位,即若對任意的 (c0,c1,···,cn?1)∈Rn,均有 v(c0,c1,···,cn?1)=(λcn?1,c0,···,cn?2).設(shè)C為R上長為n的線性碼,若對任意的(c0,c1,···,cn?1)∈C,均有

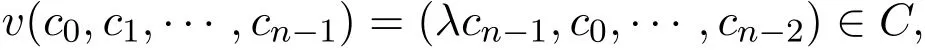
稱C為環(huán)R上長為n的λ-常循環(huán)碼.對任意的x=(x1,x2,···,xn),y=(y1,y2,···,yn)∈Rn, x,y的內(nèi)積定義為設(shè)C為有限鏈環(huán)R上長為n的線性碼,C的對偶碼定義為:

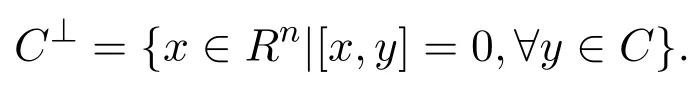
若C?C⊥稱C為自正交碼,若C=C⊥稱C為自對偶碼.

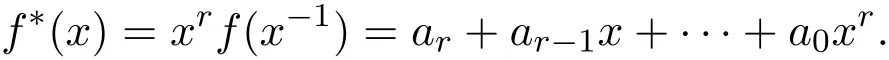
設(shè)λ為有限鏈環(huán)R上的可逆元,如果f(x)整除xn?λ(即xn?λ=f(x)g(x)),記

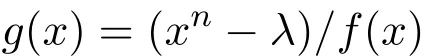
3 有限鏈環(huán)上的任意長度的常循環(huán)碼

引理3.1對于任意的i,j∈Zpm?1,若存在λ∈Zpm?1,使得i?j≡nλ(mod(pm?1))成立,則環(huán)R上的長為n的常循環(huán)碼與常循環(huán)碼置換等價,其中c1,c2,···,ce?1∈Fpm.

證明構(gòu)造映射:

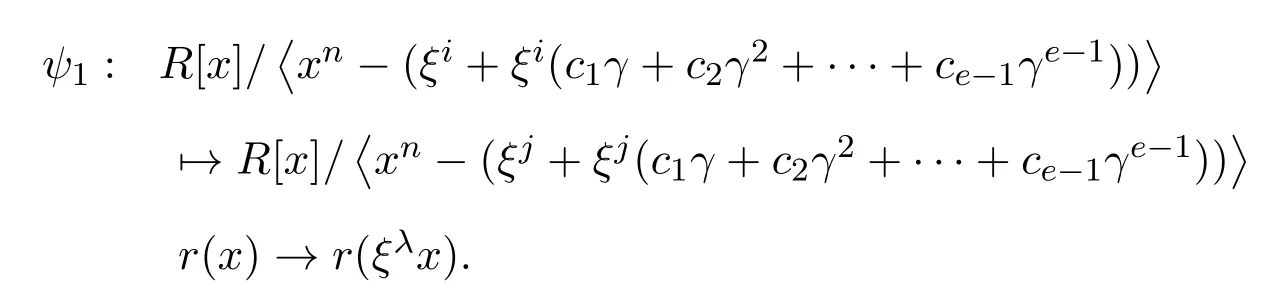
易證ψ1是環(huán)同態(tài)映射.下面證明該映射是一一映射.

對任意的f(x),g(x)∈R[x],

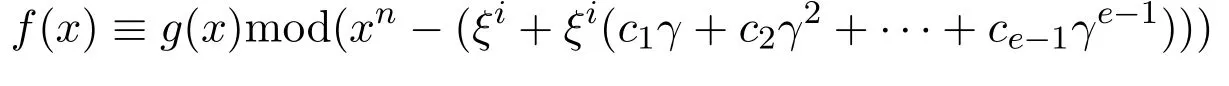
當(dāng)且僅當(dāng)存在h(x)∈R[x],使得

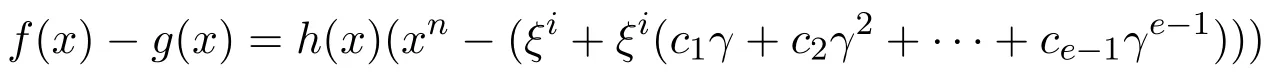
當(dāng)且僅當(dāng)

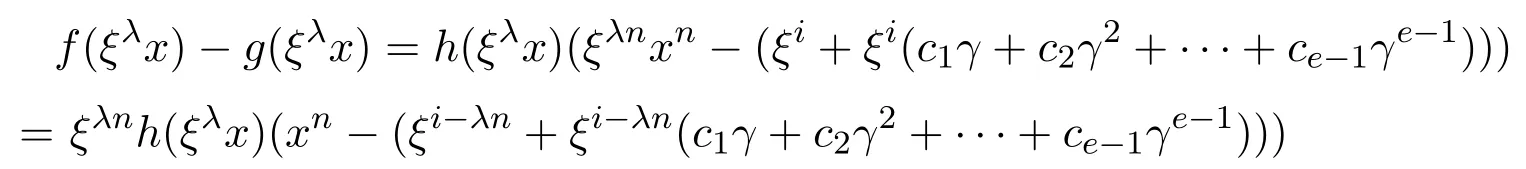
當(dāng)且僅當(dāng)

當(dāng)且僅當(dāng)

所以,ψ1是從

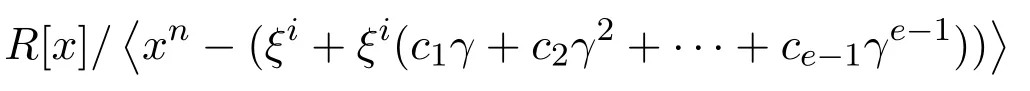
到

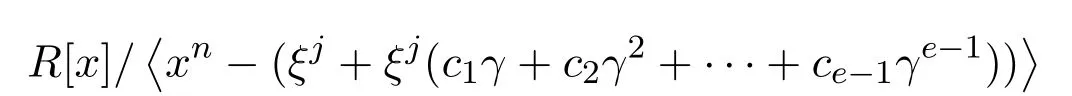
的一一映射.

所以ψ1是環(huán)同構(gòu)映射,則環(huán)R上的長為n的常循環(huán)碼與常循環(huán)碼置換等價.

用文獻(xiàn)[9]定理2.1的證明方法可得下面的定理.

定理 3.1對于任意的 i,j∈Zpm?1,若存在 i?j∈{0,l,2l,···,pm?l?1},其中 l=

(n,pm?1),則環(huán)R上長為n的常循環(huán)碼與常循環(huán)碼置換等價,其中c1,c2,···,ce?1∈Fpm.

由定理3.1易得下面的推論.

推論 3.1(1)若i∈{0,l,2l,···,pm?l?1},則環(huán)R上的長為n的ξi-常循環(huán)碼與循環(huán)碼置換等價,其中l(wèi)=(n,pm?1);

(2)對于任意的i,j∈Zpm?1,若i?j∈{0,l,2l,···,pm?l?1},其中l(wèi)=(n,pm?1),則環(huán)R上的長為n的ξi-常循環(huán)碼與ξj-常循環(huán)碼置換等價.

由推論3.1(1)及文獻(xiàn)[10]中的定理4.9可得:

定理3.2若i∈{0,l,2l,···,pm?l?1},R是一個特征為pα的有限鏈環(huán),令n=pβl這里p不整除于l,λ=min{α,pβ}.則對任意的整數(shù)k滿足1≤k≤λ,存在一個的理想C可由k個多項式生成不能由k?1個多項式生成.

4 有限鏈環(huán)上碼長與剩余域的特征互素的常循環(huán)碼

引理 4.1當(dāng)(n,p)=1時,對于任意的i,j∈Zpm?1,若存在λ∈Zpm?1使得成立,則環(huán)R上的長為n的ξi-常循環(huán)碼與(ξi+clγl+cl+1γl+1+···+ce?1γe?1)-常循環(huán)碼置換等價,其中ci∈Fpm,i=l,l+1,···,e?1,

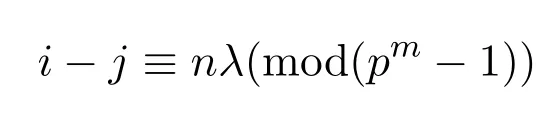
證明當(dāng)(n,p)=1時,存在n′∈Zp,使得nn′=1(mod p).構(gòu)造映射

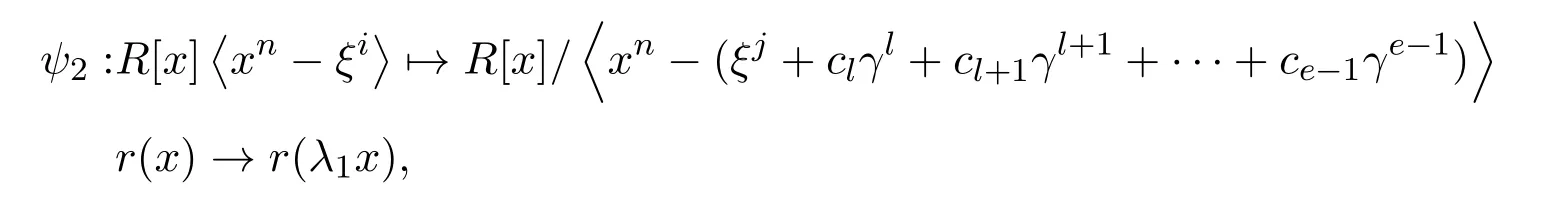
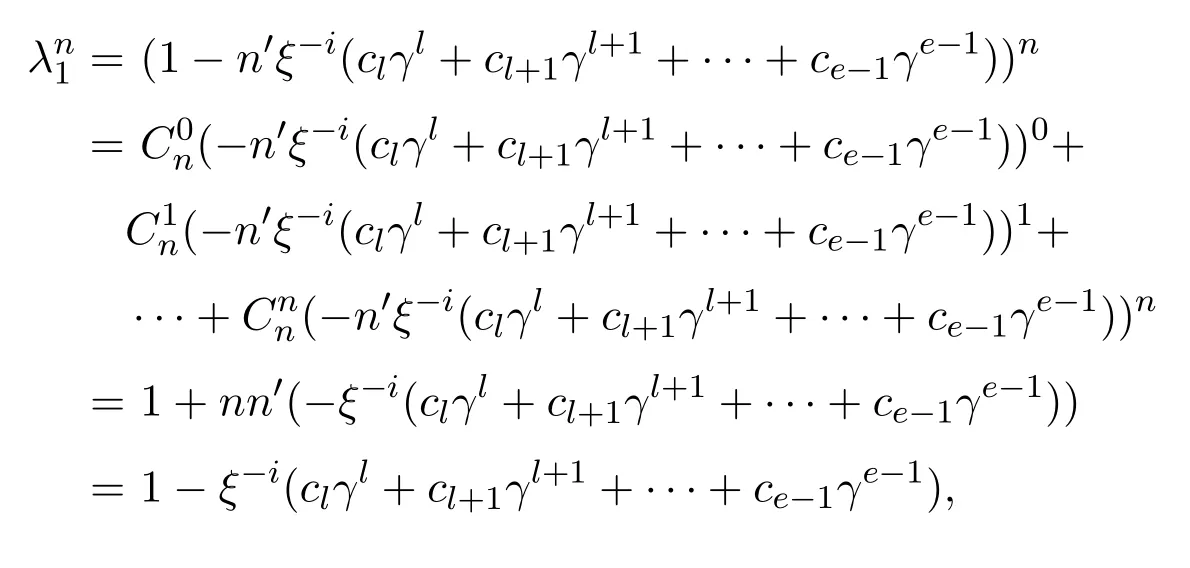
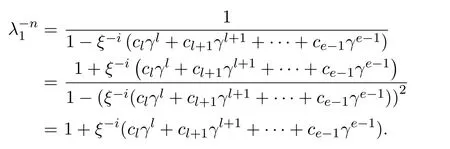
易證ψ2是環(huán)同態(tài)映射.

?f(x),g(x)∈R[x],

當(dāng)且僅當(dāng)存在h(x)∈R[x],使得

當(dāng)且僅當(dāng)

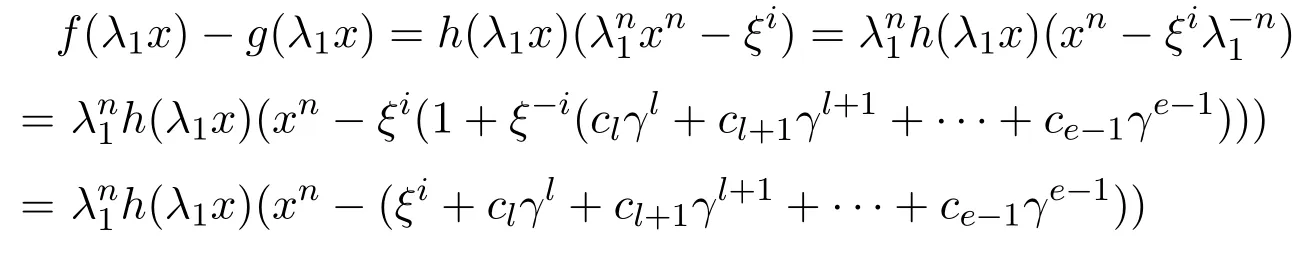
當(dāng)且僅當(dāng)

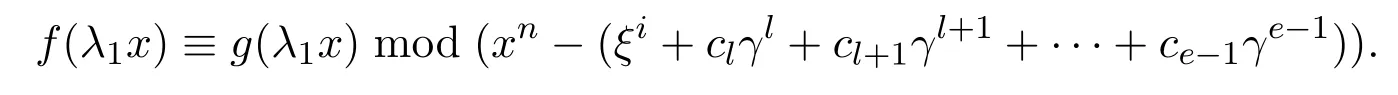
所以ψ2是從

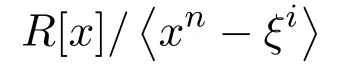
到

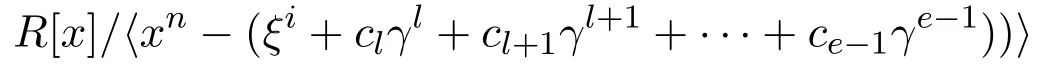
的一一映射.

所以ψ2是環(huán)同構(gòu)映射,則環(huán)R[x]上的長為n的ξi-常循環(huán)碼與常循環(huán)碼置換等價.

由推論3.1(2)及引理4.1易得下面的定理.

定理 4.1當(dāng)(n,p)=1時,若存在i?j∈{0,l,2l,···,pm?l?1},其中l(wèi)=(n,pm?1),則有限鏈環(huán)R上的長為n的常循環(huán)碼與常循環(huán)碼置換等價,其中

由定理4.1易得下面的推論.

推論 4.1若i∈{0,l,2l,···,pm?l?1},(n,p)=1,則有限鏈環(huán)R上的長為n的循環(huán)碼與常循環(huán)碼置換等價,其中ci∈Fpm,i=l,l+1,···,e?1.

引理 4.2 [8]設(shè)C為有限鏈環(huán)R上的長為n的循環(huán)碼(R的極大理想為〈γ〉,γ的冪零指數(shù)為e,R的剩余域 ˉR的特征為p,這里(n,p)=1).則存在R[x]中兩兩互素的首一不可約多項式F0,F1,···,Fe,滿足

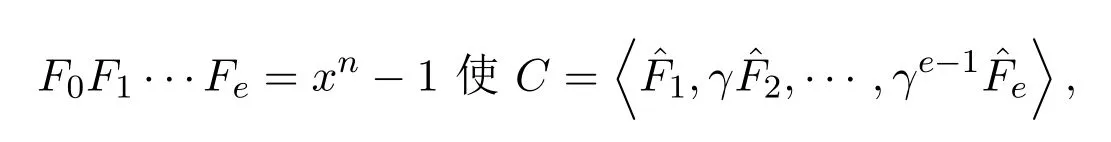
這里

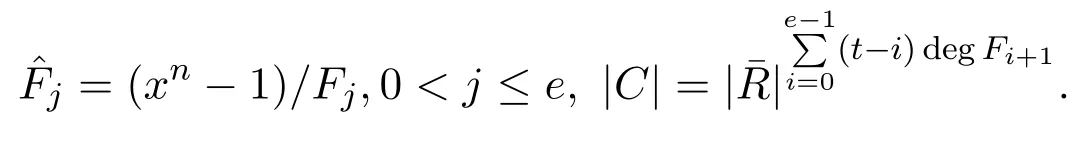
由推論4.1及引理4.2易得下面的定理.

定理 4.2設(shè)i∈{0,l,2l,···,pm?l?1},C為有限鏈環(huán)R上的長為n的(ξi+clγl+ cl+1γl+1+···+ce?1γe?1)-常循環(huán)碼(R的極大理想為〈γ〉,γ的冪零指數(shù)為e,R的剩余域Rˉ的特征為p,這里(n,p)=1).則存在R[x]中兩兩互素的首一不可約多項式F0,F1,···,Fe滿足

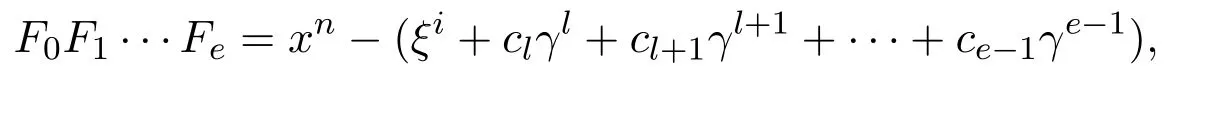
使

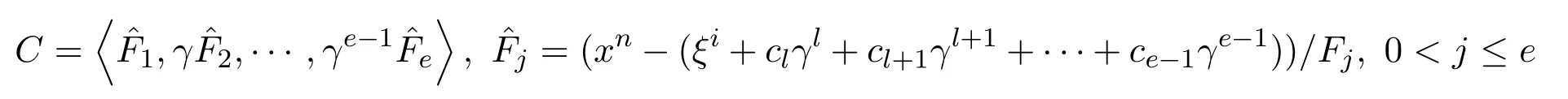
定理 4.3[8]設(shè) C為有限鏈環(huán) R上的長為 n的循環(huán)碼(R的極〈大理想為〈γ〉,γ的冪〉零指數(shù)為 e,R的剩余域的特征為 p,這里 (n,p)=1).這里 F0,F1,···,Fe為 R[x]中兩兩互素的首一不可約多項式F0F1···Fe=xn?1且Fe+1=F0,則

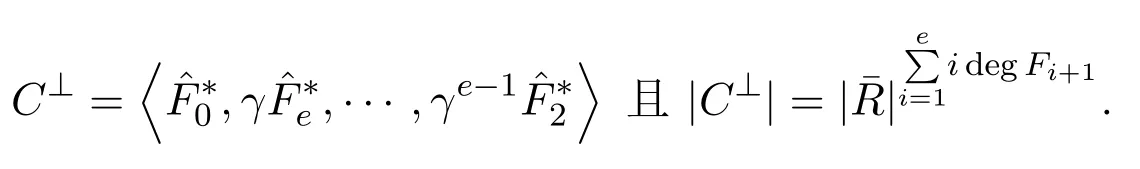
由推論4.1及定理4.3易得下面的定理.

定理 4.4設(shè) i∈{0,l,2l,···,pm?l?1},C為有限鏈環(huán) R上的長為 n的 (ξi+常循環(huán)碼 (R 的極大理想為 〈γ〉,γ的冪零指數(shù)為 e,R的剩余域 ˉR的特征為 p,這里 (n,p)=1).則存在 R[x]中兩兩互素的首一不可約多項

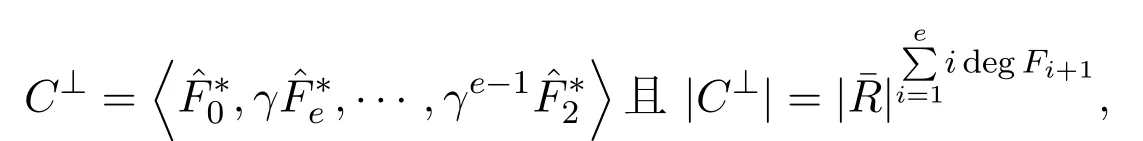
其中

5 有限鏈環(huán)上碼長ps的常循環(huán)碼

若c0,c1都是Fpm上的可逆元,則是有限鏈環(huán)R上的可逆元.則有限鏈環(huán)R上長為ps的常循環(huán)碼是環(huán)的理想.由除法原理可知,存在非負(fù)整數(shù)cq,cr,使得s=cqm+cr,0≤cr≤m?1.令則

引理5.1在環(huán)Rps上,且cx?1是該環(huán)上冪零指數(shù)為eps的冪零元.

證明對所以在環(huán)Rps上有

引理5.2[8]對有限交換環(huán)R,下面幾個條件等價

(1)R是一個局部環(huán),極大理想M為主理想環(huán);

(2)R是一個局部主理想環(huán);

(3)R是一個有限鏈環(huán).

定理5.1Rps是一個有限鏈環(huán),其所有理想按包含關(guān)系如下:

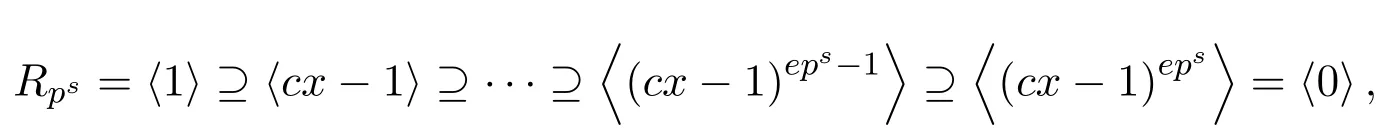
則有限鏈環(huán)R上長為ps的常循環(huán)碼就是鏈環(huán)Rps中的理想0≤i≤eps,每一個碼〈(cx?1)i〉包含pm(eps?i)個碼字.

證明因R中的每一個元素r都可以唯一的表示為ci∈Fpm～=R/〈γ〉,i=0,1,2,···,e?1.所以R[x]中每一個次數(shù)小于n的多項式f(x)都可以唯一的表示為:

這里b0i,b1i,···,b(e?1)i∈Fpm.

所以r(x)∈Rps可以表示為:

這里r0i,r1i,···,r(e?1)i∈Fpm.

因cx?1,γ是該環(huán)上的冪零元,所以r(x)可逆當(dāng)且僅當(dāng)r00/=0.由引理5.1可知r(x)不可逆,則r00=0.這時r(x)∈〈cx?1〉,所以〈cx?1〉是Rps中包含所有不可逆元的理想,所以Rps是一個極大理想為〈cx?1〉的局部環(huán),由引理5.2可知Rps是一個有限鏈環(huán).

引理 5.3 [11]有限鏈環(huán)R上的λ-常循環(huán)的對偶碼是λ?1-常循環(huán)碼.

引理 5.4 [11]有限鏈環(huán)R上的任意長為n線性碼C,|C||C⊥|=|R|n.

定理5.2當(dāng)〈pm≥e時〉,有限鏈環(huán)R上每一個長為常循環(huán)碼的對偶碼為且C⊥是環(huán)R上的常循環(huán)碼,C⊥中包含pmi個碼字,其中0≤i≤eps.

證明由因此

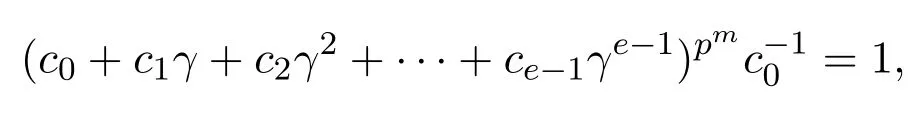
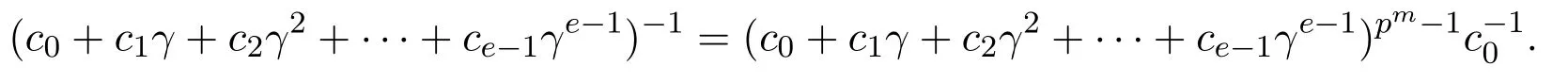
所以

6 結(jié)論

本文首先研究了有限鏈環(huán)上常循環(huán)碼的等價性,利用等價性給出了該環(huán)上常循環(huán)碼及其對偶碼的結(jié)構(gòu).今后,將進(jìn)一步研究一般有限環(huán)上常循環(huán)碼的等價性及其上常循環(huán)碼的結(jié)構(gòu).

參考文獻(xiàn)

[1] 朱士信,王立啟.環(huán)Fp+uFp+vFp+uvFp上的一類常循環(huán)碼[J].數(shù)學(xué)物理學(xué)報:A輯,2013,33(4):696-701.

[2] Dougherty S T,Karadeniz S,Yildiz B.Cyclic codes over Rk[J].Des.Codes Cryptogr,2012,63:113-126.

[3] Chen Bo cong,Fan Yun,Lin Li ren,et al.Constacyclic codes over fi nite fi elds[J].Finite Fields and Their Applications,2012,18:1217-1231.

[4] Dougherty S T,Yildiz B,Karadeniz S.Codes over Rk[J].Gray Maps Binary Images,2011,17(3):205-219.

[5] 施敏加.環(huán)F2+uF2+···+uk?1F2上的常循環(huán)自對偶碼[J].電子與信息學(xué)報,2013,41(6):1088-1092.

[6] Karadeniz S,Yildiz B.(1+v)-Constacyclic codes over F2+uF2+vF2+uvF2[J].Journal of the Franklin Institute,2011,348:2625-2632.

[7] 李巖,朱士信.環(huán) Fpm+uFpm+···uk?1Fpm上的一類常循環(huán)碼 [J].合肥工業(yè)大學(xué)學(xué)報:自然科學(xué)版, 2012,35(3):408-411.

[8] Dinh H Q,Lopez-permauth S R.Cyclic and negacyclic codes over fi nite chain rings[J].IEEE Trans.Inform. Theory,2004,50(8):1728-1744.

[9] 丁健,李紅菊,李海霞．關(guān)于環(huán)Fpm+uFpm上常循環(huán)碼的等價性[J]．中國科學(xué)技術(shù)大學(xué)學(xué)報,2013,43(4):334-339.

[10] 鄭喜英.無限長序列及有限鏈環(huán)上的循環(huán)碼[D].武漢:華中師范大學(xué),2007.

[11] Dinh H Q.Constacyclic codes of length psover Fpm+uFpm[J].Journal of Algebra,2010,324:940-950.

Constacyclic codes over fi nite chain rings

Zheng Xiying1,Kong Bo2
(1.College of Information Engineering,Huanghe Science and Technology College,Zhengzhou 450063,China; 2.School of Mathematics and Statistics,Henan Institute of Education,Zhengzhou 450046,China)

Let R be a fi nite chain ring,and the characteristic of the residue fi eldˉR be a prime number p.The equivalence of constacyclic codes over fi nite chain ring R are studied,and the structure of some constacyclic codes and their duals are given.The structure of all constacyclic codes with length psand their duals over the ring R are determined.

constacyclic code,cyclic code,dual code

O157.4

A

1008-5513(2014)04-0377-09

10.3969/j.issn.1008-5513.2014.04.007

2014-05-08.

河南省基礎(chǔ)與前沿(122300410229);河南省教育廳科學(xué)技術(shù)研究重點(diǎn)項目(14B110024);鄭州市科技局科技攻關(guān)項目(20141375).

鄭喜英(1981-),碩士,講師,研究方向：代數(shù)與編碼.

2010 MSC:47B35