Some Geometric Inequalities on the Radii of Inscribed Sphere of a Simplex and Its Subsimplex

ZHANG Han-fang

(School of Mathematics Science,Jiangsu Normal University,Xuzhou 221116,China)

Some Geometric Inequalities on the Radii of Inscribed Sphere of a Simplex and Its Subsimplex

ZHANG Han-fang

(School of Mathematics Science,Jiangsu Normal University,Xuzhou 221116,China)

In this paper,we obtain some geometric inequalities on the radii of inscribed sphere of a simplex and its subsimplex,as particular case of this paper,we obtain some main results of[1].

Euclidean space;simplex;geometric inequality

§1.Introduction

Let A be a simplex in n dimensional Euclidean space Enwith vertex set{A1,A2,···,An+1}, let r be the radius of the inscribed sphere of A and let ribe the radius of the inscribed sphere of the n?1 dimensional face A spanned by the vertex set{A1,···,Ai?1,Ai+1,···,An+1} (i=1,2,···,n+1),author of the paper[1]is given the following results

and equality is valid if and only if A is regular.

and the equalities are valid if and only if A is regular.

The main aim of this paper is to show the following three broader theorems.

§2.Main Results and Its Proofs

Theorem 1Let A be a simplex in n dimensional Euclidean space Enwith vertex set {A1,A2,···,An+1},let r the radius of the inscribed sphere of A,let rithe radius of the inscribed sphere of the n?1 dimensional face A spanned by the vertex set{A1,···,Ai?1,Ai+1,···, An+1}(i=1,2,···,n+1),α∈(0,2],then we have

with equality holds if and only if A is regular simplex.

ProofSuppose that Siis n?1 dimensional volume of A,S standthat is

with equality holds if and only if A is regular simplex.

it is easy to know that xi∈(0)in(6)and x1+x2+···+xn+1=1.

Let f(x)=(1?2x)α2and

namely

rearranging this,we obtain inequality(4),it is easy to see that necessary and sufficient conditions of equality valid are x1=x2=···=xn+1,that is A is regular simplex.Theorem 1 is proved.

Corollary 1Under the same conditions as in the Theorem 1,we have

and equality is valid if and only if A is regular.

In fact,writing

then according to Maclaurin inequality[2-4]

in(8),taking that j=1,applying(4)we obtain immediately(7).

According to Corollary 1 and applying Cauchy inequality,we can get the following corollary.

Corollary 2Under the same conditions as in the Theorem 1,we have

and equality is valid if and only if A is regular.

Theorem 2Let A be a simplex in n dimensional Euclidean space En,{A1,A2,···,An+1} stand for the vertex set of A,r(k)the radius of inscribed sphere of k dimensional simplex A(k), and A(k)spanned by the vertex set{A1,A2,···,Ak+1},then we have

with equality holds if and only if all the l dimensional subsimplices A(l)are regular.

ProofIn(9),taking k=n+1,then we have

with equality holds if and only if A is regular simplex.

Applying inequality(11)to k dimensional simplex A(k),then

applying inequality(12)to simplex A,then

that is

using recursion inequality(13),we can arrive at

namely

from(14),we obtain immediately(10).The proof of Theorem 2 is completed.

Corollary 3Under the assumptions of the previous the Theorem 2,suppose that aijdenote the distance of from the vertex Aito the vertex Aj,we have

with equality holds if and only if all the l dimensional subsimplices A(l)are regular.

In fact,taking k=1 in(10),owing to

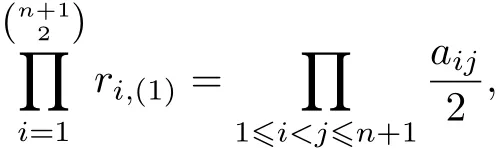
therefore

rearranging this,we obtain inequality(15).

Specially,taking l=n in(15),we have the following inequality

with equality holds if and only if A is regular simplex.

Furthermore,we take k=1 in(9),then

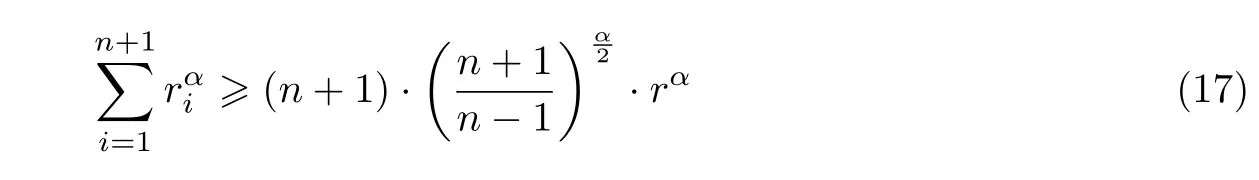
and the equality of(17)holds if and only if A is regular simplex.

Corollary 4Under the assumptions of the previous the Theorem 2,suppose that Ri,(k)denote the radius of circumscribed sphere of k dimensional subsimplex A(k),and A(k)spanned by the vertex set{Ai1,Ai2,···,Aik+1},then

with equality holds if and only if all the l dimensional subsimplices A(l)are regular.

In fact,according to well-known Euler inequality[56]R≥nr and(10),we have

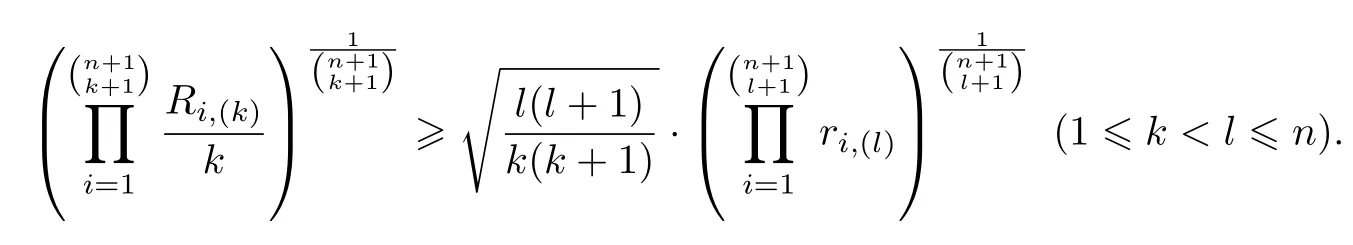
Rearranging this,we obtain immediately inequality(18).

We write that

similarly,by the(4)and(17),applying the proof method of the previous Theorem 2,we can obtain immediately the following theorem.

Theorem 3Under the assumptions of the previous the Theorem 2,suppose that α∈(0,2], then we have

with equality hold if and only if all the l dimensional subsimplices A(l)are regular.

It is easy to see that the previous inequalities(1)～(3)are the particular case of this paper, that is,some main results of[1]are the particular case of this paper.

[1]LENG Gang-song,TANG Li-hua.Some inequalities on the inradii of a simplex and of its faces[J].Geometriae Dedicata,1996,61:43-49.

[2]BECKENBACH E F,BELLMAN R.Inequalities[M].Germany:Springer-Verlag,Berlin,Heidelberg,New York,Tokyo,1983,11.

[3]MITRINOVI′C D S.Analytic Inequalities[M].Germany:Springer-Verlag,1970.

[4]BULLEN P S.A Dictionary of Inequalities[M].England:University of British Columbia,1998,192.

[5]KLAMKIN M S.Inequality fo a simplex[J].SLAM Rev,1985,27(4):576.

[6]ZHANG Han-fang.Further improvement of Klamkin inequality[J].Chinese Quarterly Journal Inequality, 2001,16(3):55-59.

tion:51K05,51M16

CLC number:O184,O178Document code:A

1002–0462(2014)02–0215–06

date:2012-07-09

Supported by the First Class Key Course of Mathematics of Jiangsu Province (SXKYA1010)

Biography:ZHANG Han-fang(1955-),male,native of Donghai,Jiangsu,a professor of Jiangsu Normal University,engages in distance geometry and inequality.