一類多線性分數(shù)次積分交換子在廣義 Morrey 空間上的有界性
周 疆,張超楠
(新疆大學數(shù)學與系統(tǒng)科學學院,新疆 烏魯木齊 830046)
1 引言及主要結(jié)果
設(shè)m,n∈, 0<α (1) 作為經(jīng)典Riesz位勢的多線性推廣, 式(1)所定義的算子已被廣泛地研究, 可參看文獻 [1-6] 及所引文獻. 一個局部可積函數(shù)b屬于 BMO(n)空間, 如果 對于β>0, 齊次Lipschitz 函數(shù)空間 Lipβ(n) 定義為 (2) 其中:m∈,b=(b1,…,bm)為一族局部可積函數(shù), 且 (3) 定理1 設(shè)ωj:n×+→+的正則函數(shù),m∈,且若是Lp1×…×Lpm→Lp有界的,bj∈Lipβ(n),則是Lp1,ω1×…×Lpm,ωm→Lp,ω有界的, 即存在常數(shù)C, 使得 首先, 介紹一些將要用到的定義和引理. 定義1[10]設(shè)正則函數(shù)ω:n×+→+, 1 其中:B(x,r)表示以點x為中心且邊長為r的球體, 則稱函數(shù)f屬于廣義 Morrey 空間. 因此廣義的 Morrey 空間是經(jīng)典 Morrey 空間和 Lebesgue 空間的推廣. 以下引理在本文證明中是必要的. 引理1[8]設(shè)Q*?Q,b(x)∈Lloc(n), 則存在常數(shù)C, 使得 |bQ-bQ*|≤C‖b‖Lipβ(n)|Q|β/n. 引理2[8]對于 0<β<1,1≤p<∞, 有 Ⅰ+Ⅱ+Ⅲ+Ⅳ. C(‖b1‖Lipβ+‖b2‖Lipβ)‖f1‖Lp1,ω1‖f2‖Lp2,ω2 對于Ⅱ, 進行分解得: |Ⅱ|≤|(b1(x)-m2B(b1))Iα,2(f1χ(2B)c,f2χ2B)(x)|+ |(b2(x)-m2B(b2))Iα,2(f1χ(2B)c,f2χ2B)(x)|+|Iα,2((b1(y)-m2B(b1))f1χ(2B)c,f2χ2B)(x)|+ |Iα,2(f1χ(2B)c,(b2(y)-m2B(b2))f2χ2B)(x)|:=Ⅱ1+Ⅱ2+Ⅱ3+Ⅱ4. 對于Ⅱ1,x∈B,y1∈(2B)c,y2∈2B, 有|(x-y1,x-y2)|~|x-y1|+|x-y2|~|x-y1|, 根據(jù) H?lder 不等式, 得 類似于Ⅱ1的估計, 對于Ⅱ2, 有 對于Ⅱ3, 由引理1,引理2及H?lder 不等式, 得 類似于Ⅱ3的估計, 對于Ⅱ4, 有 綜合以上的估計, 有 同樣, 對于Ⅲ, 有 下面證明對Ⅳ也有同樣的估計, 首先對Ⅳ 進行如下分解: |Ⅳ|≤|(b1(x)-m2B(b1))Iα,2(f1χ(2B)c,f2χ(2B)c)(x)|+ |(b2(x)-m2B(b2))Iα,2(f1χ(2B)c,f2χ(2B)c)(x)|+|Iα,2((b1(y)-m2B(b1))f1χ(2B)c,f2χ(2B)c)(x)|+ |Iα,2(f1χ(2B)c,(b2(y)-m2B(b2))f2χ(2B)c)(x)|:=Ⅳ1+Ⅳ2+Ⅳ3+Ⅳ4. 對于Ⅳ1,x∈B,y1∈(2B)c,y2∈(2B)c, 有 |x-y1|~|x-y2|, 根據(jù)H?lder 不等式, 得 同理可得: 類似的證明方法, 也有 以及 結(jié)合上面對Ⅳ1,Ⅳ2,Ⅳ3,Ⅳ4的估計, 有 綜上所述, 得 定理證明完畢. 參考文獻: [1]Bernardis A, Salinas O. Two-weight norm inequalities for the fractional maximal operator on spaces of homogeneous type [J]. Studia Math, 1994, 212(3): 201-207. [2]Chen Xi, Xue Qingying. Weighted estimates for a class of multilinear fractional type operators [J]. J Math Anal Appl, 2010, 362: 355-373. [3]Grafakos L. On multilinear fractional integrals [J]. Hokkaido Math J, 1998, 27(1): 219-232. [4]Lian Jiali, Ji Li, Wu Huoxiong. Multilinear commutators of BMO functions and multilinear singular integrals with non-smooth kernels [J]. Appl Math J Chinese Univ, 2011, 26(1): 109-120. [5]Moen K. Weighted inequalities for multilinear fractional integral operators [J]. Collect Math, 2009, 60: 213-218. [6]Muckenhoupt B, Wheeden R L. Weighted norm inequalities for fractional integral [J]. Trans Amer Math Soc, 1974, 192: 261-274. [7]Chanillo S. A note on commutators [J]. Indiana Univ Math J, 1982, 31: 7-16. [8]Paluszyński M. Characterization of the Besov spaces via the commutator operators of Coifman, Rochberg and Weiss [J]. Indiana Univ Math J, 1995, 44(1):1-17. [9]Pérez C, Torres R. Sharp maximal function estimates for multilinear singular integrals [J]. Contemp Math, 2003, 320: 323-331. [10]Softova L. Singular integrals and commutators in generalized Morrey spaces [J]. Acta Math Sinica, English Series, 2006, 22(3): 757-766.
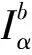

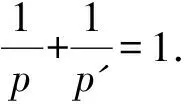
2 基本引理

3 定理的證明






