陳 頌,閆曉芳

(永城職業(yè)學(xué)院 基礎(chǔ)部,河南 永城 476600)

0 引言

p-Laplace方程是一類橢圓微分方程.含有p-Laplace算子的微分方程解的存在性問(wèn)題受到了廣泛的關(guān)注,相關(guān)研究結(jié)果可參見(jiàn)文獻(xiàn)[1-3]等.p(t)-Laplace方程首先是從非線性彈性理論中引發(fā)出來(lái)的,p(t)-Laplace算子比p-Laplace算子有更復(fù)雜的非線性性質(zhì),相關(guān)結(jié)果可參見(jiàn)文獻(xiàn)[4-6]等.

本文討論了如下p(t)-Laplace方程解的存在性問(wèn)題:

(1)

其中p∈C(,)是T-周期函數(shù),對(duì)于t∈有p(t)>1,f∈C(×N,N),且f(t,u)關(guān)于t是T-周期的.

1 定理

定理如果存在r>0和線性向量場(chǎng)V,使得對(duì)任意的u∈N,〈Vu,u〉≥0,當(dāng)且僅當(dāng)u=0時(shí),〈Vu,u〉=0,且對(duì)所有的t∈[0,T],u∈N,當(dāng)〈Vu,u〉=r時(shí),都有〈f(t,u),Vu〉>0,〈f(t,u),V*u〉>0,則以上方程至少有一個(gè)解u滿足|u(t)|≤r,其中t∈[0,T].

令g∈C([0,T]×N,N).設(shè)X是Banach空間,定義映射A:X→X*:

定義映射G:X→X*:

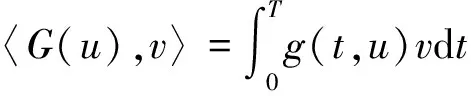
引理[7]令p為定理中所定義的,A,g,G均為上文定義.若存在一個(gè)正常數(shù)M,使得

|g(t,u)|≤M,

(2)

?t∈[0,T],?u∈N,

則映射A+G:X→X*是滿的.特別地,存在u∈X使得A(u)+G(u)=0,且u是以下問(wèn)題的解:

(3)

定義映射Q=Qr:N→N:

令g(t,u)=f(t,Q(u))-Q(u).則g∈C(×N,N).

則由引理,映射A+G:X→X*是滿的.特別地,存在u∈X使得A(u)+G(u)=0,且u是以下問(wèn)題的解:

(4)

現(xiàn)在證明u滿足|u(t)|≤r,?t∈[0,T].首先證明以下論斷.

論斷存在t∈[0,T],使得|u(t)|≤r.

證明反證法.設(shè)對(duì)所有的t∈[0,T]都有|u(t)|>r.考慮函數(shù)

φ(t)=〈|u′(t)|p(t)-2u′(t),Vu(t)〉,

t∈[0,T],

故

φ′(t)=|u′(t)|p(t)+

〈f(t,Qu(t)),Vu(t)〉+

〈u(t)-Qu(t)〉,t∈[0,T].

因?yàn)閨Qu(t)|=r,有

〈f(t,Qu(t)),Vu(t)〉≥0,

又因

故

〈u(t)-Qu(t),Vu(t)〉=

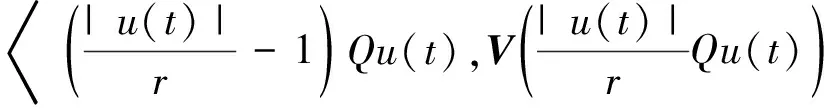
(|u(t)|-r)|u(t)|>0.

故

φ′(t)>0, ?t∈[0,T].

(5)

這表明φ′(t)在[0,T]上嚴(yán)格增,這和φ(0)=φ(T)矛盾.故論斷成立.

2 定理的證明

假設(shè)u不滿足|u(t)|≤r,?t∈[0,T],則存在t∈[0,T],使得|u(t)|>r.假設(shè)u在上定義,且為T(mén)-周期的,則u∈C1(,N).設(shè)

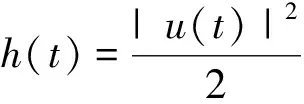
由假設(shè),可以找到σ<τ使得

h(σ)=maxh(t),

|u(τ)|=r,t∈,

且當(dāng)t∈[σ,τ]時(shí),|u(t)|>r.故|u(σ)|>r且h′(σ)=0.

令

ψ(t)=〈u(t),Vu(t)〉,

ψ1(t)=〈u′(t),Vu(t)〉,

ψ2(t)=〈u(t),Vu′(t)〉.

類似于式(5)的證明,有

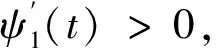
將V換成V*,同理可得

〈u′(t),V*u(t)〉′>0, ?t∈[σ,τ],

則

〈V′u(t),u(t)〉′>0, ?t∈[σ,τ],

故

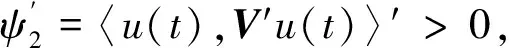
故

ψ″(t)=〈u(t),Vu(t)〉″=

(〈u′(t),Vu(t)〉′+

〈u(t),Vu′(t)〉′=

因此,ψ′(t)在[σ,τ]上嚴(yán)格增.由于

因此,對(duì)t∈[σ,τ],有h′(t)

故u滿足

|u(t)|≤r,?t∈[0,T].

故可推出Qu(t)=u(t).因此u是問(wèn)題(4)的解,故u是問(wèn)題(1)的解.定理得證.

參考文獻(xiàn):

[1] MAWHIN J. Some boundary value problems for Hartman-type perturbations of the ordinary vectorp-Laplace[J]. Nonlinear Analysis: Real World Applications, 2000, 40(1/8): 497-503.

[2] KNOBLOCH H W. On the existence of periodic solutions for second order vector differential equations[J]. Journal of Differential Equations, 1971, 9(1): 67-85.

[3] ZEIDLER E. Nonlinear Functional Analysis and Its Applications, Part 2 B: Nonlinear Monotone Operators[M]. New York: Springer-Verlag, 1990.

[4] FAN Xianling, WU Hongqing, WANG Feizhi, et al. Hartman-type results forp(t)-Laplace systems[J]. Nonlinear Analysis: Real World Applications, 2003, 52: 585-594.

[5] FAN Xianling, ZHAO Yuanzhang, ZHAO Dun, et al. Compact inbedding theorems with symmetry of Strauss-Lions type for the spaceW1p(x)(Ω)[J]. Journal of Mathematical Analysis and Applications, 2001, 255: 333-348.

[6] FAN Xianling, ZHAO Dun. On the spacesLp(x)(Ω) andWm,p(x)(Ω)[J]. Journal of Mathematical Analysis and Applications, 2001, 263: 424-446.

[7] FAN Xianling, FAN Xing. A knobloch-type result forp(t)-Laplace systems[J]. Journal of Mathematical Analysis and Applications, 2003, 282: 453-464.

[8] MUSIELAK J. Orlicz Spaces and Modular Spaces: Lecture Notes in Mathematics, Vol. 1034[R]. Berlin: Springer-Verlag, 1983.

[9] ADAMS R A. Sobolev Spaces[M]. New York: Academic Press, 1975.

[10] ODEN J T. Qualitative Methods on Nonlinear Mechanics[M]. New Jersey Englewood Cliffs: Prentice-Hall, 1986.