Relativistic Bound and Scattering Amplitude of Spinless Particles in Modi fi ed Schioberg Plus Manning–Rosen Potentials

B.H.Yazarlooand H.Mehraban

Physics Department,Semnan University,P.O.Box 35195-363,Semnan,Iran

1 Introduction

In the relativistic and nonrelativistic quantum mechanics,the scattering state solution of the relativistic and nonrelativistic wave equation plays an important role for some physical potential.

Recently,there has been an increased interest in studying the scattering state solutions for nonrelativistic quantum mechanics[1?4]and Scattering state of Dirac equation is investigated under cusp and Coulomb as well in Refs.[5–6]it is well known that the scattering state solutions of the Klein-Gordon equation for some physical potentials are very important since they contain all the necessary information for the relativistic quantum system under consideration,these potentials are of Eckart,Manning–Rosen,Woods–Saxon,Yukawa,and Hulthen.[7?12]Schi¨oberg potential function is a better description for the potential energy of a molecular vibration than the Morse potential function,and it represents also intermolecular interactions.Some authors have used the Schi¨oberg potential function to investigate the rotation and vibration of diatomic molecules.[13?16]Chen etal.[17]studied the nonlinear optical properties in a quantum well with the Schi¨oberg potential.As we know Manning–Rosen potential(MRP)is a central interaction.[18]The central potentials are used in all branches of physics.In particle and high-energy physics,they describe the quark interactions.[19]In nuclear physic,[20]atomic physics[21?22]they have been used to investigate the intermolecular interactions and atomic pair correlation functions[22?23]and it has been applied to study the vibration modes diatomic molecules.[24?25]The organization of the present paper is as follows,after a brief introductory of scattering state in Sec.2,we obtain the energy eigenvalues for bound state of modi fi ed Schioberg plus Manning–Rosen potential.In Sec.3 the calculation of scattering amplitude is presented,and in last section some special cases of the potential,such as Manning Rosen potential and modi fi ed Schioberg potential respectively are reported.

2 Bound State Solutions

The radial part of D-dimensional Klein–Gordon(KG)equation in the presence of scalar S(r)and vector V(r)potentials can be written as(~=c=1)[26?27]

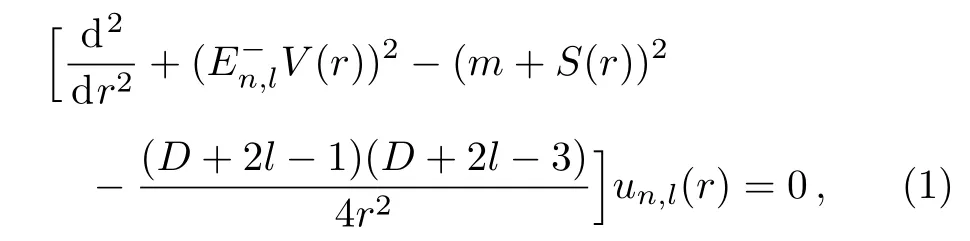
where m andEn,lrepresent the rest mass and energy of the spinless particle,respectively.Under the equal scalar and vector modi fi ed Schioberg plus Manning–Rosen potentials

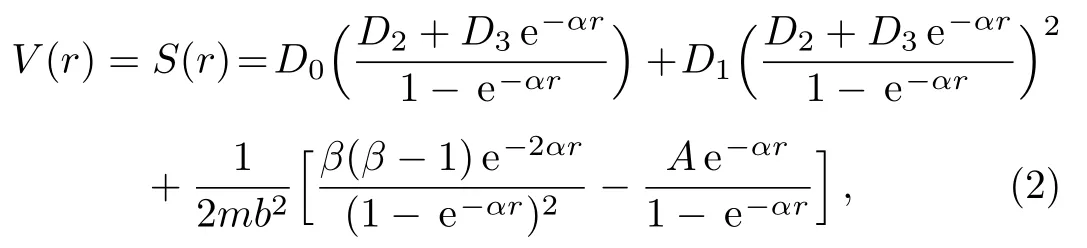
where D0,D1,D2,D3,σ,β,α,and b are potential constants,the KG equation is written as

where we have used the following approximation for the centrifugal term

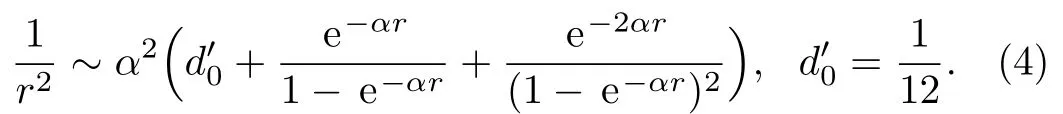
By introducing a new variable of the form z=exp(?αr),Eq.(3)is transformed to the following analytically solvable form

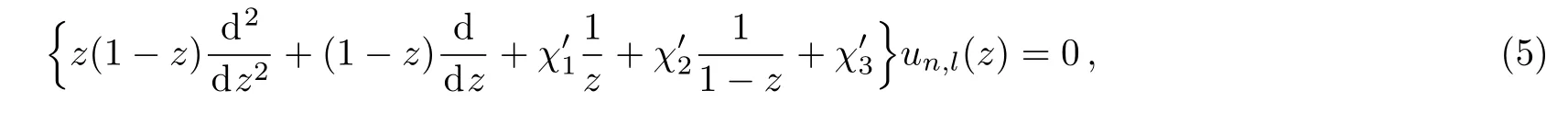
where

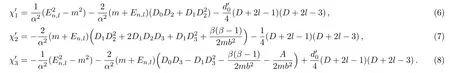
By taking the wave function of the form

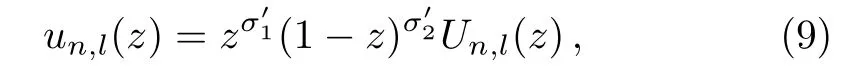
Eq.(5)reduces to

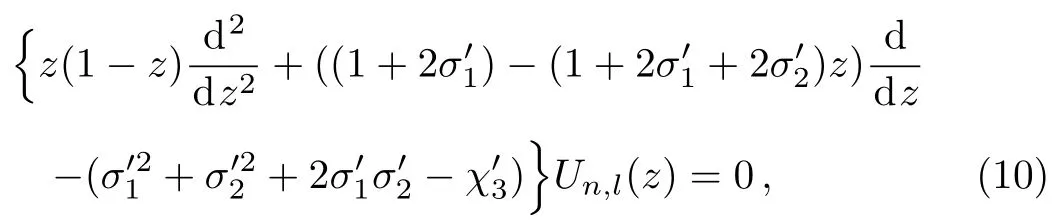
where

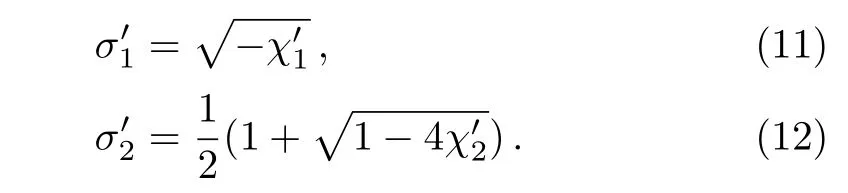
By de fi ning

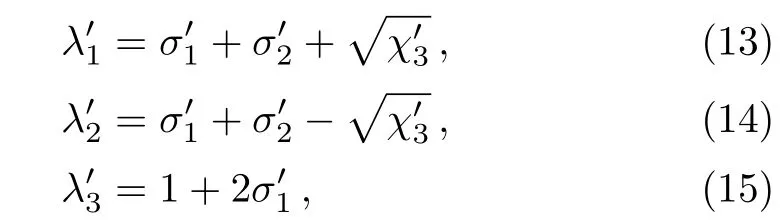
Eq.(10)can be written as

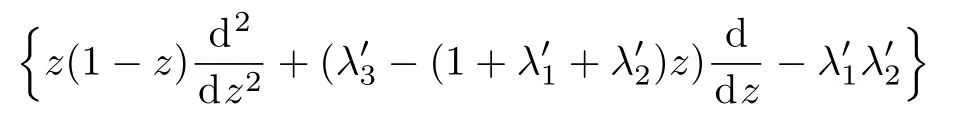
Eq.(16)is the hypergeometric equation,and its solution is the hypergeometric function.Therefore we have

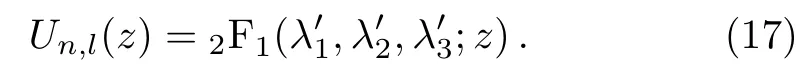
And the wave function has the form

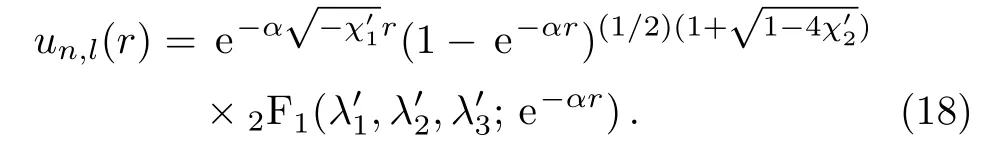
To have a fi nite solutionshould be a negative integer,this gives us the following equation

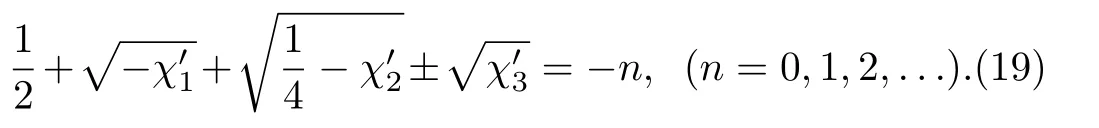
Equation(19)gives us equation of energy eigenvalues of KG equation under the equal scalar and vector Schioberg plus Manning–Rosen potentials.For D=1–4,we have reported some numerical results for different states in Table 1.It is clear that the energy shows a degenerate behavior when l increases to l+1 and D reduces to D?2,i.e.

Table 1 The bound-state energy levels Enlfor m=1/2,α =0.05,d′0=1/12,D0= ?1,D1=0.5,D2=0.3,D3= ?0.9,β=0.2,b=1,A=1/2.__________________________________________________________________________________________

3 Scattering State Solutions

In this section we intend to obtain the scattering states for the modi fi ed Schioberg plus Manning–Rosen potentials(D=3)and l=0,therefore we start from Eq.(3).Using a new variable of the form y=1? e?αr,Eq.(3)becomes

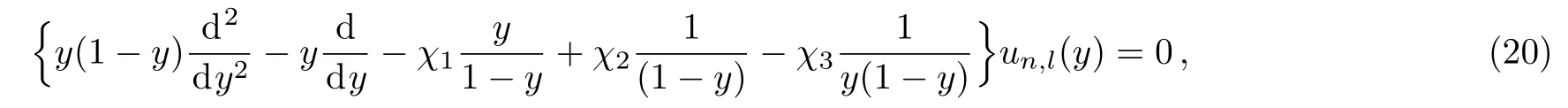
where

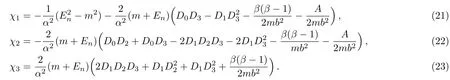
To obtain hypergeometric differential equation from Eq.(20),we use a new transformation

which gives hypergeometric-type equation for gn,l(y)as

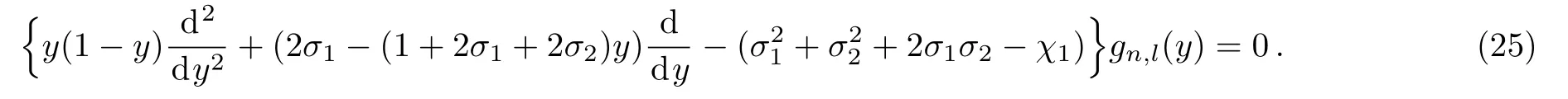
The solution of Eq.(25)is hypergeometric function

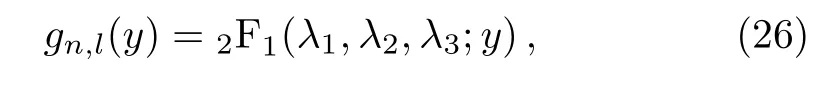
where

Thus,the radial wave function of scattering states is

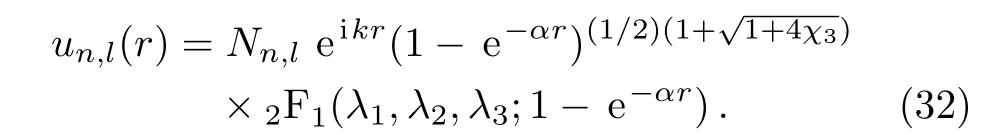
We now study the asymptotic form of the above expression for large r,and calculate the normalization constant of radial wavefunctionsNn,land phase shifts.From formulaes(27)–(29),we have

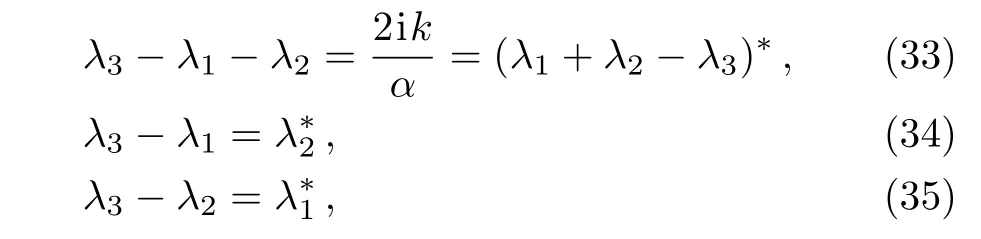
and by applying the following properties of heypergeometric function[27?28]

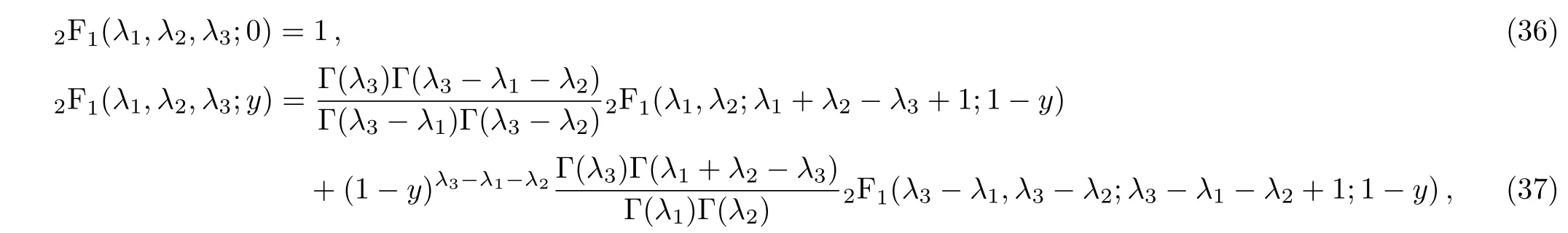
we can write Eq.(32)as

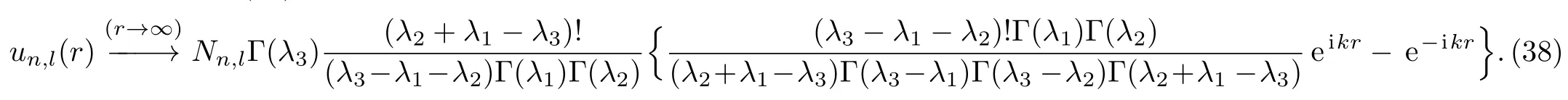
The asymptotic behavior for the wave function is given by(for l=0)[29?30]

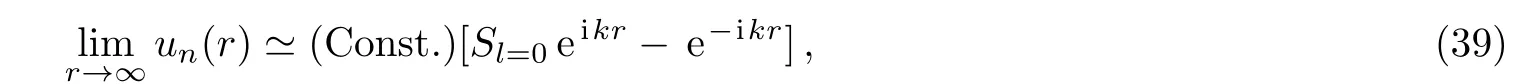
by comparing Eq.(38)with Eq.(39),we find

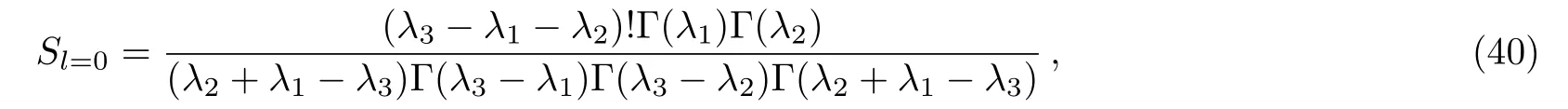
or equivalently,from Eqs.(27)–(29),we can easily obtain

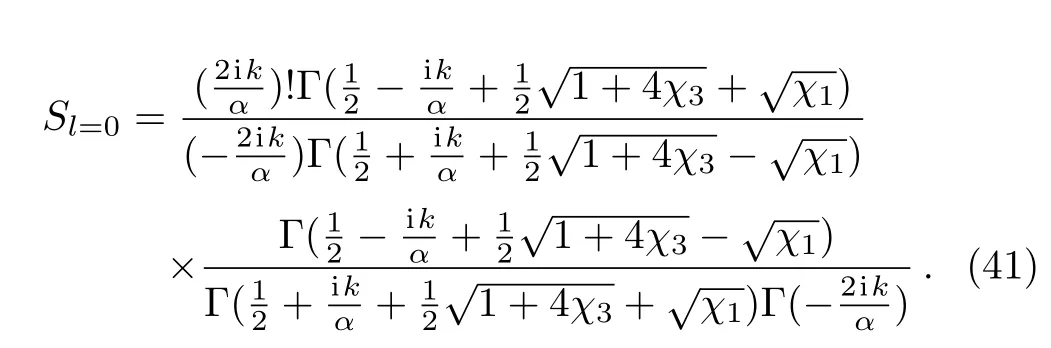
Therefore,the total cross section can be easily obtained from

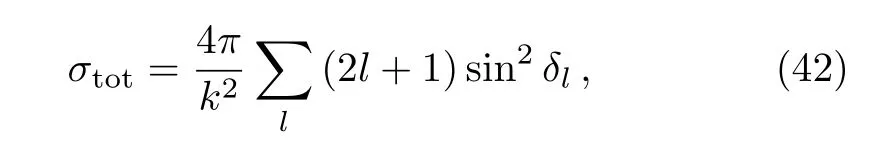
where

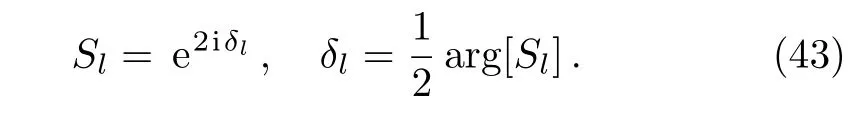
4 Discussion

We are now going to study some special cases of our results.

4.1 Bound and Scattering States Solutions for Manning–Rosen Potential

By choosing D0=D1=0,the modi fi ed Schioberg plus Manning–Rosen potentials reduces into Manning–Rosen potential,

In this case we obtain the following relations for bound states solution of Manning–Rosen potential

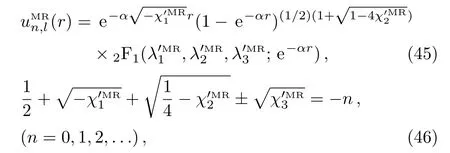
with

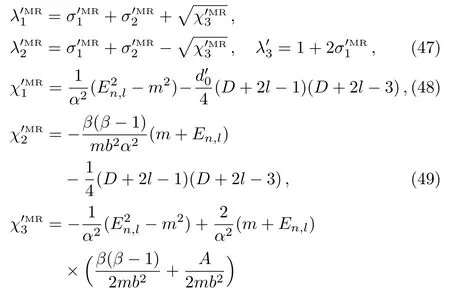
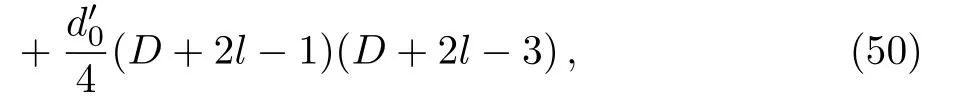
and the scattering amplitude can be given by

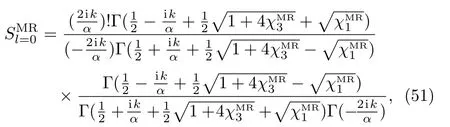
where

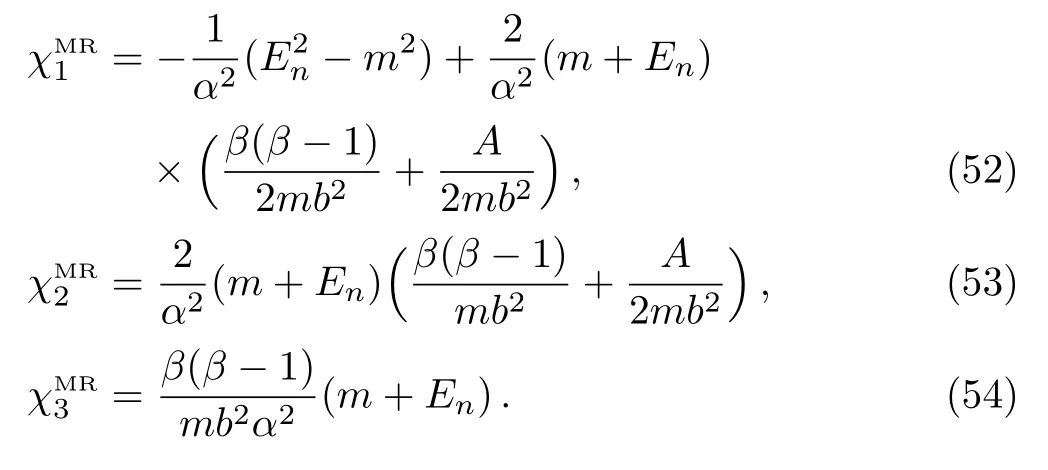
5 Bound and Scattering States Solutions for Modi fi ed Schioberg Potential

If we consider β =A=0(or β =1,A=0),modi fi ed Schioberg plus Manning–Rosen potentials turns into the modi fi ed Schioberg potential

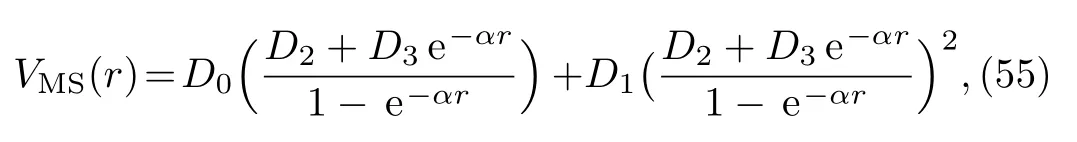
according to our results,bound states solution of modi fi ed Schioberg potential in this limit is

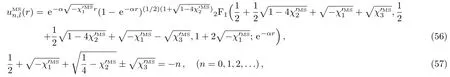
where

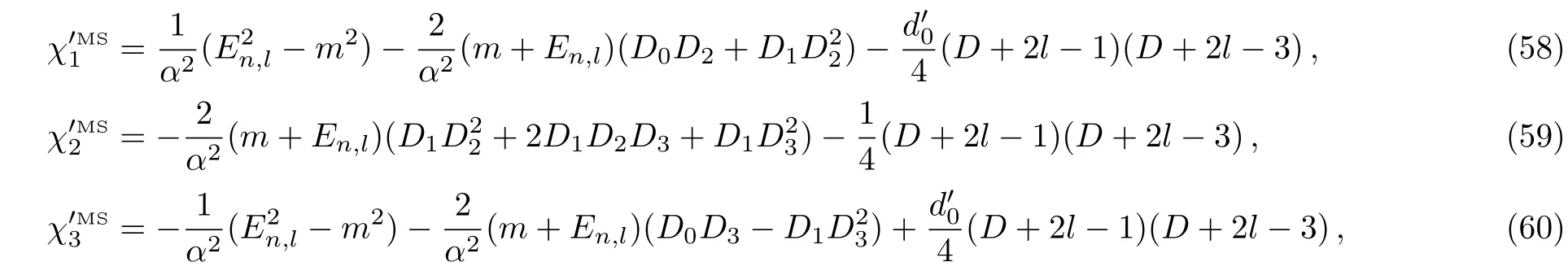
and for the scattering amplitude we have

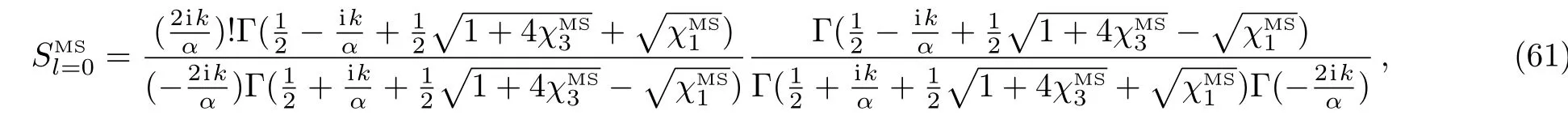
with

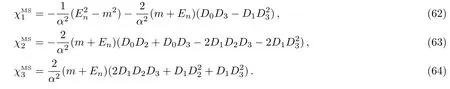
6 Conclusions

In the present work we studied the scattering states solutions of the K–G equation under the equal scalar and vector modi fi ed Schioberg plus Manning–Rosen potentials.The radial wave functions in terms of hypergeometric functions and the energy eigenvalues for bound states are obtained and some numerical results are reported.We considered some special cases of as Manning–Rosen potential and modi fi ed Schioberg potential,respectively.These results may lead to many interesting applications in the different quantum mechanical systems.

References

[1]W.G.Feng,C.Y.Long,D.X.Yong,and S.H.Dong,Phys.Scr.77(2008)035001.

[2]G.F.Wei,C.Y.Long,and S.H.Dong,Phys.Lett.A 372(2008)2592.

[3]G.F.Wei,W.C.Qiang,and W.L.Chen,Cent.Eur.J.Phys.8(2010)574.

[4]A.Arda,O.Aydogdu,and R.Sever,Phys.Scr.84(2011)025004.

[5]Y.Jiang,S.H.Dong,A.Antill′on,and M.L.Cassou,Eur.Phys.J.C 45(2006)525.

[6]S.H.Dong and M.L.Cassou,Phys.Lett.A 330(2004)168.

[7]G.F.Wei,S.H.Dong,and V.B.Bezerra,Int.J.Mod.Phys.A 24(2009)161.

[8]G.F.Wei,Z.Z.Zhen,and S.H.Dong,Cent.Eur.J.Phys.7(2009)175.

[9]C.Rojas and V.M.Villalba,Phys.Rev.A71(2005)052101.

[10]A.Arda and R.Sever,J.Math.Phys.52(2011)092101.

[11]G.F.Wei,X.Y.Liu,and W.L.Chen,Int.J.Theor.Phys.48(2009)1649.

[12]Z.M.Cang,Chin.Phys.B 17(2008)1274.

[13]P.Q.Wang,J.Y.Liu,L.H.Zhang,S.Y.Cao,and C.S.Jia,J.Mol.Spectrosc.278(2012)23.

[14]D.Schi¨oberg,Mol.Phys.59(1986)1123.

[15]J Lu,Phys.Scr.72(2005)349.

[16]C.Berkdemir,J.Math.Chem.46(2009)492.

[17]T.Chen,W.Xie,and S.Liang,Physica B 407(2012)263.

[18]M.F.Manning and N.Rosen,Phys.Rev.44(1933)943.

[19]A.A.Khelashvili,Theor.Math.Phys.51(1982)447.

[20]J.N.Ginocchio and A.Leviatan,Phys.Lett.B425(1998)1.

[21]M.V.Zhukov,B.V.Danilin,D.V.Fedorov,J.S.Vaagen,F.A.Gareev,and J.Bang,Phys.Lett.B 265(1991)19.

[22]A.Arda and R.Sever,J.Math.Chem.(2012)DOI:10.1007/s10910-012-0011-0.

[23]A.Rahan,F.H.Stillinger,and H.L.Lemberg,J.Chem.Phys.63(1975)5223.

[24]R.J.Le Roy and R.B.Bernstein,J.Chem.Phys.52(1970)3869.

[25]E.Romera,P.S′anchez-Moreno,and J.S.Dehesa,J.Math.Phys.47(2006)103504.

[26]H.Hassanabadi,B.H.Yazarloo,S.Zarrinkamar,and H.Rahimov,Commun.Theor.Phys.57(2012)339.

[27]H.Hassanabadi and B.H.Yazarloo,Indian J.Phys.DOI 10.1007/s12648-013-0317-1.

[28]H.Hassanabadi,B.H.Yazarlooa,S.Hassanabadia,S.Zarrinkamarb,and N.Salehi,Acta Phys.Pol.A 124(2013)20.

[29]F.Cooper,A.Khare,and U.Sukhatme,Phys.Rep.251(1995)267.

[30]R.K.Yadav,A.Khare,and B.P.Mandal,Ann.Phys.331(2013)313.