具有冪零奇點的七次Hamilton系統(tǒng)Abel積分的零點個數(shù)估計

馬慧龍,楊紀華

(寧夏師范學(xué)院數(shù)學(xué)與計算機科學(xué)學(xué)院,寧夏固原 756000)

具有冪零奇點的七次Hamilton系統(tǒng)Abel積分的零點個數(shù)估計

馬慧龍,楊紀華

(寧夏師范學(xué)院數(shù)學(xué)與計算機科學(xué)學(xué)院,寧夏固原 756000)

本文研究了具有冪零奇點的七次Hamilton 系統(tǒng)的Abel積分的零點個數(shù)問題.利用Picard-Fuchs方程法,得到了Abel積分上零點個數(shù),其中 Γh是,所定義的卵形線和是x和y的次數(shù)不超過n的多項式.

Hamilton系統(tǒng);冪零奇點;Abel積分;Picard-Fuchs方程

1 引言

考慮如下Hamilton系統(tǒng)的擾動向量場

其中0＜|ε|?1,H(x,y)是關(guān)于x和y的m+1次實多項式,f(x,y)和g(x,y)是關(guān)于x和y的次數(shù)不超過n的實多項式.假設(shè)系統(tǒng)(1.1)的未擾動系統(tǒng)(1.1)ε=0有連續(xù)閉軌線族{Γh},Σ為Γh的最大存在開區(qū)間,即

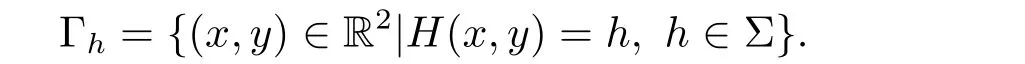
考慮以下積分

(1.2)式稱為Abel積分.尋找Abel積分零點個數(shù)的最小上界Z(m,n)稱為弱Hilbert 16問題或Hilbert-Arnold問題[1].相關(guān)的研究很多.例如,Khovansky和Varchenko獨立地證明了Z(m,n)的有限性,但是沒有給出具體的表達式[2,3].李承治和張芷芬得到了Z(2,2)=2[4].對于H(x,y)=y2+x3?x,Horozov和Iliev通過研究相應(yīng)的Picard-Fuchs方程得到Z(2,n)≤5n+15[5].另外,Petrov分別研究了Hamilton函數(shù)H(x,y)=y2?x+x3,H(x,y)=y2+x2?x4和H(x,y)=y2?x2+x4的相應(yīng)Abel積分I(h)的零點的個數(shù)[6?9].對于4次Hamilton函數(shù)H(x,y)=?x2+x4+y4和H(x,y)=x2+y2+ax4+y4,Zhou和Li得到了相應(yīng)Abel積分零點個數(shù)的上界[10,11].當m＞4時,由于很難得到Abel積分I(h)的代數(shù)結(jié)構(gòu),目前研究結(jié)果很少[10].

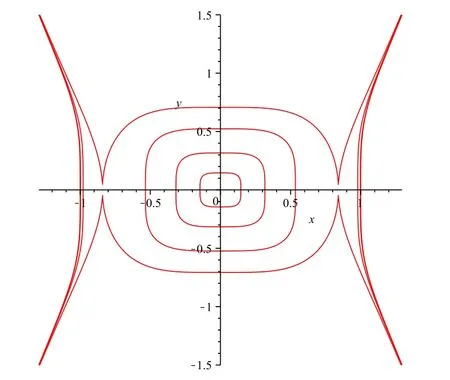
圖1:系統(tǒng)(1.4)的相圖

受文獻[5,10,11]的啟發(fā),本文研究八次Hamilton函數(shù)

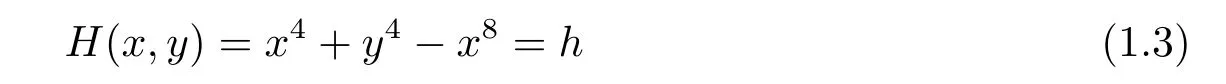
相應(yīng)的向量場

記B(n)為Abel積分I(h)在上的零點個數(shù)(計重數(shù)),其中n=max{degf,degg}.本文的主要結(jié)果為

定理1.1對Hamilton函數(shù)

B(n)≤而且B(1)=0,其中[·]是取整函數(shù).

2 Abel積分I(h)的代數(shù)結(jié)構(gòu)

由分部積分公式可知

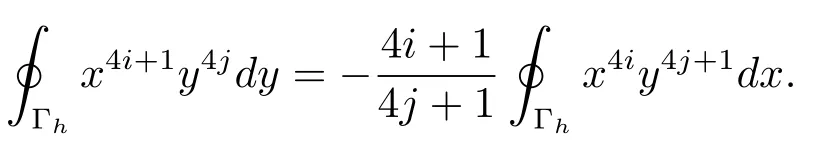
引理2.1假設(shè)n≥5,對于Hamilton函數(shù)(1.3),I(h)可表示為

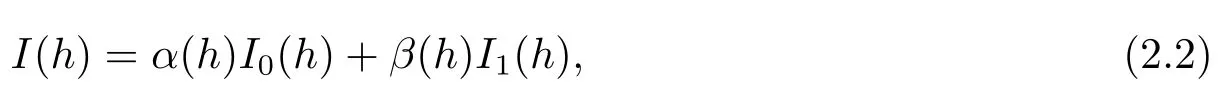
其中α(h)和β(h)是關(guān)于h的多項式,且k和k?1分別是degα(h)和degβ(h)的最小上界.

證分兩步進行證明.

(1)證明對n=4i+4j+1=4k+1≥5,積分I4i,4j+1可以表示為Il,m(l+m=4k?3)和hIl,m(l+m=4k?7或4k?3)的線性組合.

事實上,對(1.3)式兩端同時關(guān)于x求導(dǎo)可得

(2.3)式兩端同乘以x4i?7y4j+1dx并沿著Γh積分可得

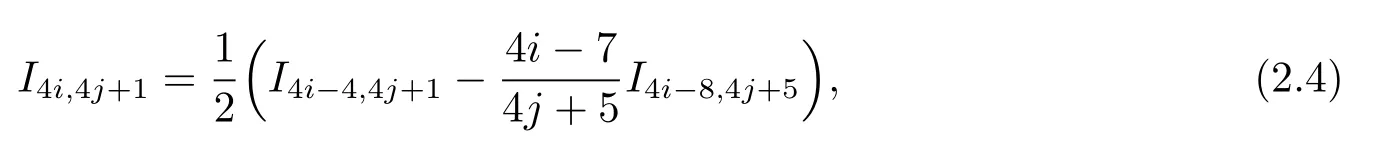
其中i≥2.(1.3)式兩端同乘以x4iy4j?3并沿著Γh關(guān)于x積分可得

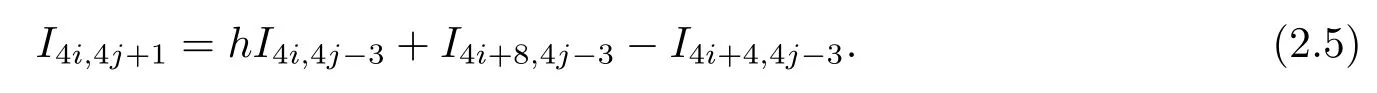
由(2.4)式可得

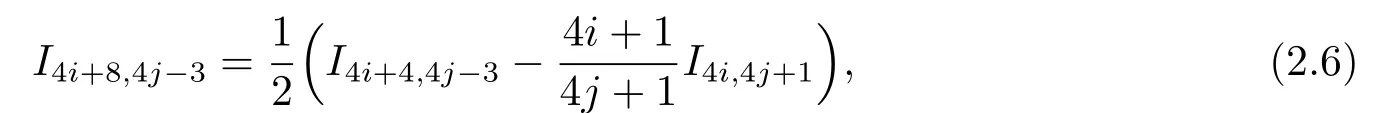
把(2.6)式代入(2.5)可得

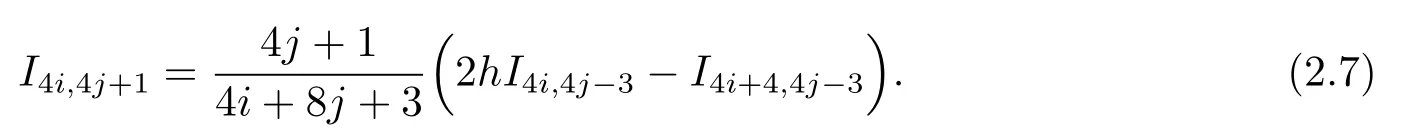
由(2.5)式可得

把(2.8)式代入(2.4)式可得

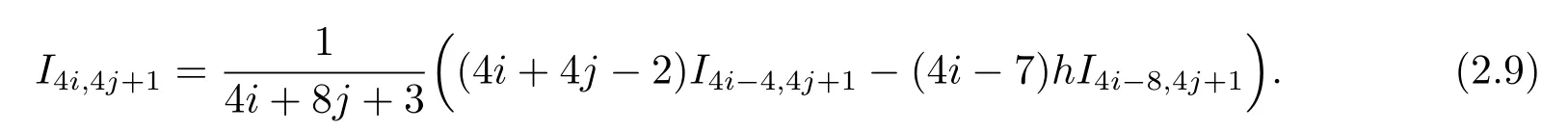
在(2.7)式中分別取(i,j)=(0,k),(1,k?1),在(2.9)式中分別取(i,j)=(2,k?2),(3,k?3),···,(k?1,1),(k,0),可得

計算可得|A|=1,且B中元素僅含有積分Il,m(l+m=4k?3)和hIl,m(l+m=4k?7或4k?3).

(2)用數(shù)學(xué)歸納法證明I(h)=α(h)I0(h)+β(h)I1(h),并且

事實上,由(2.7)和(2.9)式可得

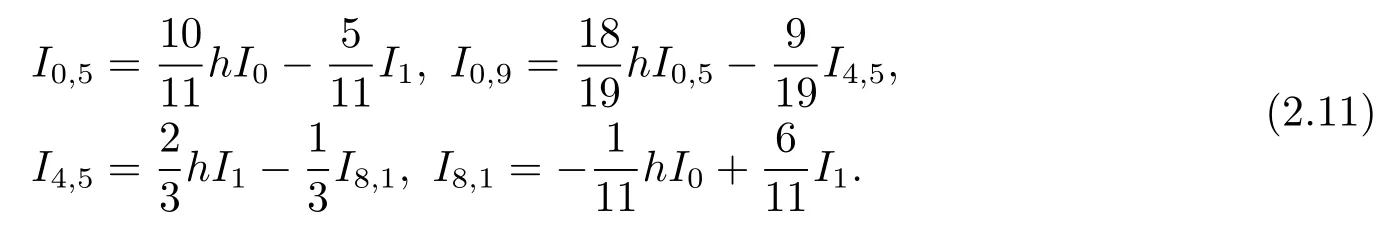
即當k=1,2時結(jié)論成立,其中n=4k+1.假設(shè)當k≤s?1時,結(jié)論成立.那么當k=s時,由等式(2.10)和第1步的結(jié)論可得

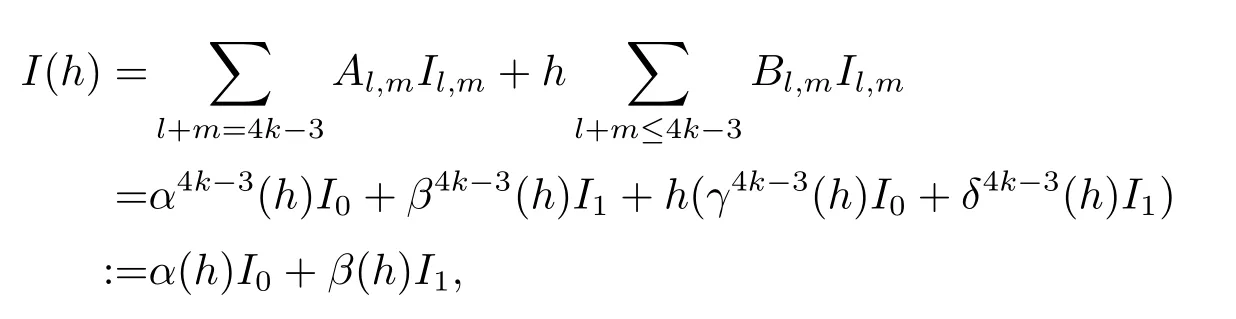
其中degα4k?3(h),degγ4k?3(h)≤k?1,degβ4k?3(h),degδ4k?3(h)≤k?2.因此

即對任意的n,并且k和k?1分別是degα(h)和degβ(h)的最小上界.證畢.

3 Picard-Fuchs方程和Riccati方程

本小節(jié)將得到I0和I1滿足的Picard-Fuchs方程.

引理3.1對于Hamilton函數(shù)(1.3),I0和I1滿足Picard-Fuchs方程

證(1.3)式兩端同時關(guān)于h求導(dǎo)可得進而可得

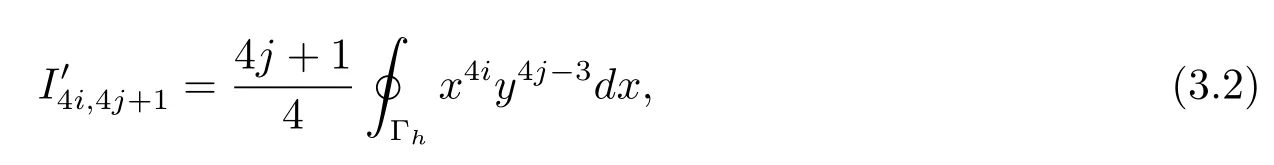
所以

(3.2)式兩端同乘以h可得

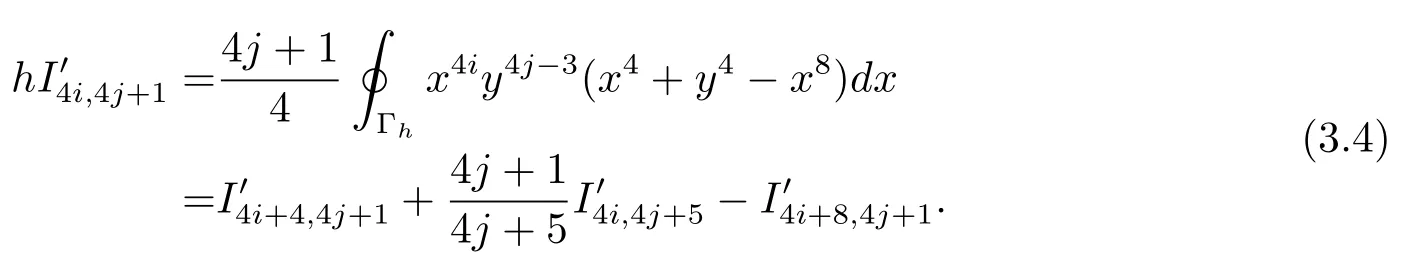
另一方面,

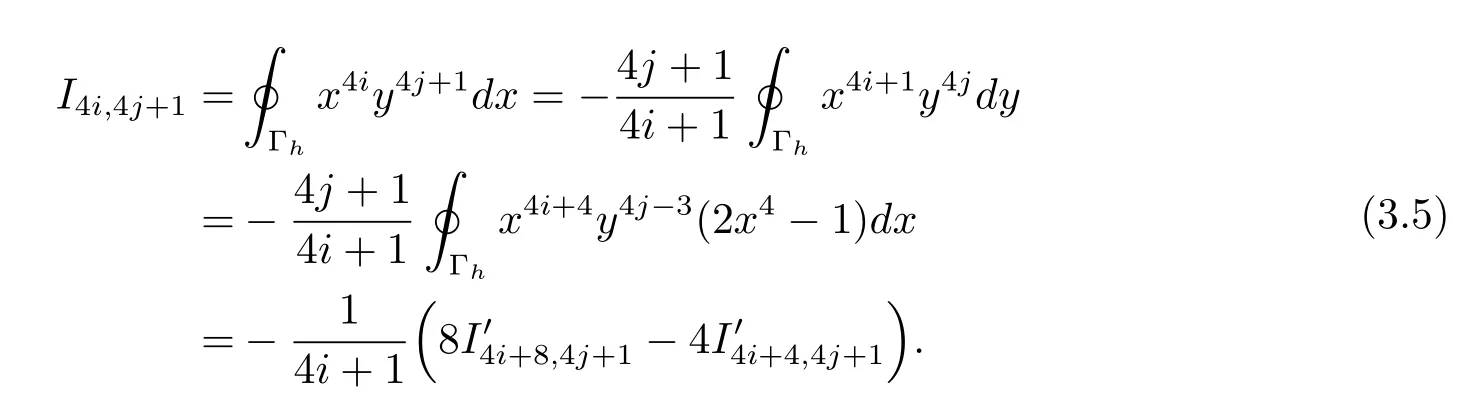
由(3.3)–(3.5)式可得

在(3.6)式中分別取(i,j)=(0,0)和(1,0)可得

注意到(2.11)式即可得結(jié)論成立.證畢.

引理3.2對于Hamilton函數(shù)(1.3),滿足如下的Riccati方程

證由于結(jié)合(3.1)式即可得(3.8)式.證畢.

4 主要結(jié)果的證明

引理4.1設(shè)則W(h)滿足

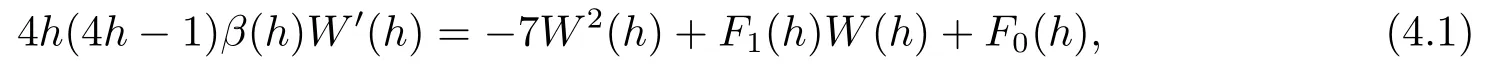
其中degF0(h)≤2p,F1(h)=4h(4h?1)β′(h)+2(4h+1)β(h)+14α(h),

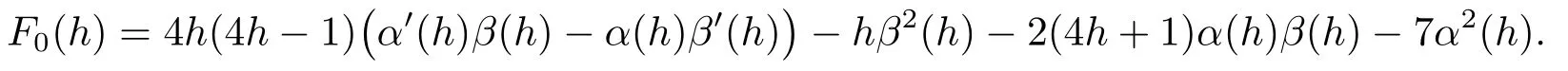
證因為所以W′(h)=α′(h)+β′(h)ω(h)+β(h)ω′(h).注意到(3.8)式即可得證.證畢.

引理4.2假設(shè)Σ0=(a,b)?Σ,則在Σ0上有#W(h)≤#F0(h)+#β(h)+1,其中#W(h)表示W(wǎng)(h)在Σ0上零點的個數(shù)(計重數(shù)).

證分兩步進行證明.

(1)如果α(h)和β(h)沒有公因子,則W(h)和β(h)沒有公共零點.設(shè)ξ1,ξ2,···,ξk是β(h)在 Σ0中的所有根,ξ0=a,ξk+1=b,ξj＜ ξj+1,j=0,1,2,···,k.設(shè)F0(h)在(ξj,ξj+1)中有ηj個零點.記h1,h2是W(h)在(ξj,ξj+1)中的兩個相鄰零點,則

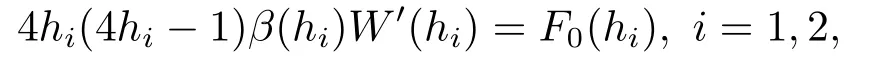
所以在(ξj,ξj+1)中F0(h1)F0(h2)≤0,也就是說W(h)在(ξj,ξj+1)中的任何兩個相鄰零點之間至少有F0(h)的一個零點.因此W(h)在(ξj,ξj+1)中至多有ηj+1個零點,進而可得

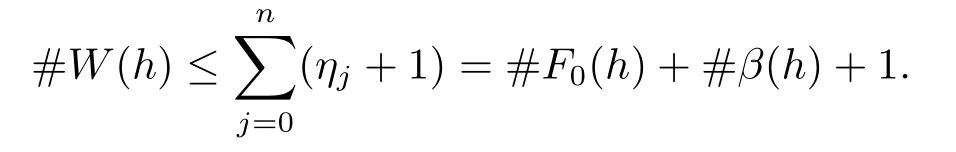
(2)如果α(h)和β(h)有公因子ν(h),記其中對于W1(h)按照(1)的證明過程可得結(jié)論成立.證畢.

定理1.1的證明當n≥5時,因為且I0(h)≠0,所以在上,W(h)與I(h)的零點個數(shù)相同.由引理4.2知

當n=1時,I(h)=c0I0,其中c0為非零常數(shù).因為I0≠0,所以B(1)=0.證畢.

[1]Arnold V.Loss of stability of self-oscillation close to resonance and versal deformation of equivariant vector fields[J].Funct.Anal.Appl.,1977,11:1–10.

[2]Khovansky A.Real analytic manifolds with finiteness properties and complex Abelian integrals[J].Funct.Anal.Appl.,1984,18:119–128.

[3]Varchenko A.Estimate of the number of zeros of an Abelian integral depending on a parameter and limit cycles[J].Funct.Anal.Appl.,1984,18:98–108.

[4]Li C,Zhang Z.Remarks on 16th weak Hilbert problem forn=2[J].Nonlinearity,2002,15:1975–1992.

[5]Horozov E,Iliev I.Linear estimate for the number of zeros of Abelian integrals with cubic Hamiltonians[J].Nonlinearity,1998,11:1521–1537.

[6]Petrov G.Number of zeros of complete elliptic integrals[J].Funct.Anal.Appl.,1984,18:148–149.

[7]Petrov G.Elliptic integrals and their nonoscillation[J].Funct.Anal.Appl.,1986,20:37–40.

[8]Petrov G.Complex zeros of an elliptic integral[J].Funct.Anal.Appl.,1987,21:247–248.

[9]Petrov G.Complex zeros of an elliptic integral[J].Funct.Anal.Appl.,1989,23:160–161.

[10]Zhou X,Li C.Estimate of the number of zeros of Abelian integrals for a kind of quartic Hamiltonians with two centers[J].Appl.Math.Comput.,2008,204:202–209.

[11]Zhou X,Li C.On the algebraic structure of Abelian integrals for a kind of pertubed cubic Hamiltonian systems[J].J.Math.Anal.Appl.,2009,359:209–215.

ON THE NUMBER OF ZEROS FOR ABEL INTEGRALS OF HAMILTON SYSTEM OF SEVEN DEGREE WITH NILPOTENT SINGULARITIES

MA Hui-long,YANG Ji-hua
(School of Mathematics and Computer Science,Ningxia Normal University,Guyuan 756000,China)

In this paper,we study the number of zeros for Abel integrals of Hamilton system of seven degree with nilpotent singularities. By using the Picard-Fuchs equation method,we derive that the number of zeros of Abel integralson the open intervalis at mostwhere Γhis an oval lying on the algebraic curveandare polynomials ofxandyof degrees not exceedingn.

Hamilton system;nilpotent singularity;Abel integral;Picard-Fuchs equation

34C07;34C05

O175

A

0255-7797(2017)06-1227-07

2016-07-29接收日期:2017-06-20

國家自然科學(xué)基金(11701306);寧夏師范學(xué)院重點科研項目(NXSFZD1708;NXSFZD1606).

馬慧龍(1975–),男,寧夏固原,講師,主要研究方向:微分方程及其應(yīng)用.