Automatic differentiation based discrete adjoint method for aerodynamic design optimization on unstructured meshes
Yisheng Gao,Yizhao Wu,Jian Xia
College of Aerospace Engineering,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China
Automatic differentiation based discrete adjoint method for aerodynamic design optimization on unstructured meshes
Yisheng Gao,Yizhao Wu*,Jian Xia
College of Aerospace Engineering,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China
Automatic differentiation(AD);Discrete adjoint;Navier-Stokes equations;Optimization;Unstructured meshes
A systematic methodology for formulating,implementing,solving and verifying discrete adjoint of the compressible Reynolds-averaged Navier-Stokes(RANS)equations for aerodynamic design optimization on unstructured meshes is proposed.First,a general adjoint formulation is constructed for the entire optimization problem,including parameterization,mesh deformation,flow solution and computation of the objective function,which is followed by detailed formulations of matrix-vector products arising in the adjoint model.According to this formulation,procedural components of implementing the required matrix-vector products are generated by means of automatic differentiation(AD)in a structured and modular manner.Furthermore,a duality-preserving iterative algorithm is employed to solve flow adjoint equations arising in the adjoint model,ensuring identical convergence rates for the tangent and the adjoint models.A three-step strategy is adopted to verify the adjoint computation.The proposed method has several remarkable features:the use of AD techniques avoids tedious and error-prone manual derivation and programming;duality is strictly preserved so that consistent and highly accurate discrete sensitivities can be obtained;and comparable efficiency to hand-coded implementation can be achieved.Upon the current discrete adjoint method,a gradient-based optimization framework has been developed and applied to a drag reduction problem.
1.Introduction
The advances in computational fluid dynamics(CFD)and high performance computers have enabled the coupling of CFD and numerical optimization techniques to effectively determine the optimum aerodynamic shape of complex configuration.Among several optimization algorithms for aerodynamic design problems,adjoint method1is now widely used since it allows one to compute the gradient(or derivatives)of an objective function ef ficiently by solving an additional linear problem that is of the same order of magnitude of a single flow solution and essentially independent of the number of design variables.Two types of adjoint approaches have been established:continuous2–5and discrete.6–10In the continuous adjoint approach,the adjoint equations and the corresponding boundary conditions are first derived by the linearization of the governing partial differential equations(PDEs)and then discretized.This approach allows the flexible discretization of the derived PDEs,reducing the CPU and memory overheads.On the other hand,the discrete adjoint is constructed by reversing the above order of the linearization and the discretization.The advantage of the discrete adjoint approach is that one can obtain the exact discrete gradient of the objective function and verify it with great precision using the complexstep method11or dual number automatic differentiation(DNAD)method.12The discrete version is also conceptually straightforward.As will be illustrated in the following section,in finite dimensional vector space endowed with the Euclidean inner product where the discretized flow equations are defined,adjoint operator is equivalent to the transpose of the matrix form of the linear operator.Thus,in concept,the formulation of the discrete adjoint only involves transpose operation,which is much simpler than the continuous counterpart.
However,the implementation of the discrete adjoint method remains a challenging task due to the difficulty associated with the exact linearization of the underlying sophisticated numerical schemes and turbulence models.Hand-coded implementation is tedious and error-prone,resulting in lengthy code development time.Moreover,some approximations or simplifications are often made in hand-coded implementation,such as the neglect of the differentiation of artificial dissipation or the assumption of constant eddy-viscosity.These approximations or simplifications lead to inaccurate discrete gradient of the objective function,and may in turn affect the optimization process.13One promising way to address this implementation issue is the use of automatic differentiation(AD).14If the source code of the original flow solver is provided,AD tools can generate codes capable of calculating the required derivatives in an automatic manner.AD tools usually offer two different modes of operation:the forward(or tangent)mode and the reverse(or adjoint)mode.In the forward mode,the derivatives are propagated in the same direction of the original flow solver,while in the reverse mode the propagation of the derivatives is reversed.The reverse mode of AD technique is analogous to the discrete adjoint and the computational cost is independent of the number of input variables,thereby very suitable for the construction of the discrete adjoint code.Unfortunately,a ‘black-box’application of the reverse mode to the entire flow solver will usually result in very inefficient codes with excessive CPU and memory overheads because of the high computational cost and storage of intermediate variables in the reversed propagation of the derivatives.To tackle this problem,a strategy of selective application of AD tools to the original CFD code has been promoted and adopted in both structured and unstructured solvers.15–19AD tools are piecewise applied to the original solver,and the derived codes are manually assembled in an appropriate reverse order,eliminating unnecessary computation and memory consumption which occur in the ‘black-box’application of AD tools.But the existing AD-assisted discrete adjoint solvers on unstructured grids are still not as efficient as hand-coded version.
In this paper,the main objective is to establish a systematic methodology for the development of accurate and efficient discrete adjoint solver on unstructured meshes,including adjoint formulation,detailed implementation,solution of adjoint equations and verification.First,a general adjoint formulation proposed by Mavriplis20is adopted to construct the adjoint model of the entire optimization problem,including parameterization,mesh deformation,flow solution and computation of the objective function.And then detailed formulations of matrix-vector products arising in the adjoint model are presented for the subsequent application of AD tools.Based on these formulations,procedural components of implementing the matrix-vector products are generated by the reverse mode of AD tools in a structured and modular manner.Upon these procedural components,a duality-preserving iterative algorithm,21,22which is exact adjoint of the iterative algorithm used in the original flow problem,is developed for the iterative solution of the flow adjoint equations.In order to verify the discrete adjoint solver,a three-step strategy is adopted:first the complex-step method is applied to the entire optimization problem;the tangent model is then verified with the result of the complex-step method;finally the adjoint computation is verified by checking the duality between the tangent and adjoint models.
The proposed methodology for developing discrete adjoint solver offers several advantages:
(1)Reduced development effort.Compared to hand-coded adjoint implementation,the use of AD tools in the proposed method avoids tedious and error-prone manual derivation and programming of detailed computational procedures for the adjoint model,substantially reducing the development difficulty and time.
(2)Consistent and accurate gradient.Since duality is strictly preserved in adjoint implementation and the dualitypreserving iterative algorithm is developed for the solution of the flow adjoint equations,the gradient of the objective function calculated by the adjoint model is consistent with the one obtained by the tangent model or other exact numerical differentiation methods in the sense of machine precision,not only for the final converged result,but also for intermediate values throughout each iteration.
(3)High efficiency.For AD-assisted discrete adjoint solver on structured grids,the transposed Jacobian arising in the adjoint model can be calculated once and explicitly stored to attain good performance.16,18However,this storage is often unaffordable in the case of unstructured grids due to much larger neighbors-to-neighbors stencil,especially for 3D problems.Therefore,using AD tools to generate codes of computing matrix-vector products in the adjoint model without explicit storage is preferred.For the existing AD-assisted adjoint solvers on unstructured meshes,the runtime of the flow adjoint computation is usually 2–5 times that of the flow solution,owing to the computation and storage of immediate variables.15,17Recently,Albring et al.used C++Expression Template technique to efficiently implement the reverse mode of AD for developing a discrete adjoint solver within the open-source multi-physics framework SU2,23obtaining a runtime ratio equal to 1.17 for inviscid flow.24In the current work,based on the structured and modular implementation of the procedural components,the computation and storage overheads are drastically reduced,so one single turbulent flow adjoint computation only costs about 10%more time than one single turbulent flow solution.This demonstrates that for the Reynolds-averaged Navier-Stokes(RANS)equations,the proposed method can deliver comparable efficiency to hand-coded implementation which usually costs the same or less amount of time as or than the flow solution.22
The rest of the paper is organized as follows.In Section 2,the definition of adjoint and duality principle are first introduced,which are followed by the general tangent and adjoint formulations,and then detailed formulations of the matrixvector products involved in the tangent and the adjoint models are presented.The application of AD tools for the detailed implementation of matrix-vector products is presented in Section 3.The solution techniques for the tangent and adjoint models are given in Section 4.The verification is discussed in Section 5.In Section 6,a discrete adjoint based optimization framework is developed and applied to a drag reduction problem.Finally,conclusions are summarized in Section 7.
2.Definition of adjoint and adjoint formulation
2.1.Definition of adjoint and duality principle
To clarify the nature of discrete adjoint,the mathematical definition of adjoint(or the formal term,adjoint operator)is first introduced.This brief introduction follows the description of Ref.25and more related mathematical theories can be found in any standard functional analysis textbook.
Definition 1.Adjoint of a linear operator


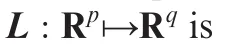
Using the definitions of the Euclidean inner product inH1andH2
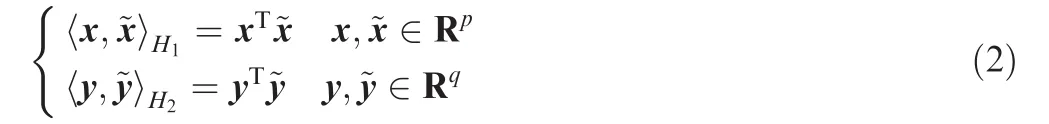
Eq.(1)can be written as

namely

Since this relation is satisfied by all x and y,it follows that

Thus,in finite dimensional linear space,discrete adjoint is simply transpose operation.This indicates that discrete adjoint is very simple and straightforward in concept,and lays a foundationforsubsequent adjointformulation andimplementation.Eq.(3)is well-known as duality principle,26which will be used for the verification of adjoint implementation in Section 5.
2.2.General adjoint formulation
In this paper,a general adjoint formulation proposed by Mavriplis20is adopted to provide an underlying framework for the subsequent detail derivation and implementation,since this formulation presents a clear construction of discrete adjoint for the entire optimization problem and is more straightforward than the traditional formulation using the terminology of Lagrange multipliers.26For aerodynamic design optimization problem,usually a set of design variables D are specified and the minimum of an objective function L(e.g.drag coefficient)is pursued.The entire process,from parameterization to computation of the objective function,referred to as the primal problem,consists of the following steps:
(1)Parameterization
When design variables are specified and an initial computational mesh is given,a parameterization method is used to produce new coordinates of surface mesh points,which can be written as

whereXsurfrepresentsthecoordinatesofsurfacemeshnodesand Fathe functional expression of the parameterization method.
(2)Mesh deformation
Once the coordinates of surface mesh points are updated,a mesh deformation method can be used to determine new coordinates of volumetric mesh points,which can be written as

where Xallrepresents the coordinates of all mesh nodes and Fbthe functional expression of the mesh deformation method.For mesh deformation methods such as spring analogy method27or linear elasticity analogy method,28Eq.(7)can be further written as

where K represents the stiff matrix arising in the discretization of mesh motion equations,dXallthe displacements of all mesh nodes and dXsurfthe displacements of surface mesh nodes.
(3)Flow solution
The flow variables are obtained by solving the discretized flow equations on the deformed mesh,which can be written as

where W represents the conservative variables and R the flow residuals.According to implicit function theorem,Eq.(9)implies that there exists a function Fcsuch that

(4)Computation of the objective function
Once the flow variables and the coordinates of mesh points are determined,the objective function can be calculated as

Accordingly,the primal problem can be expressed as
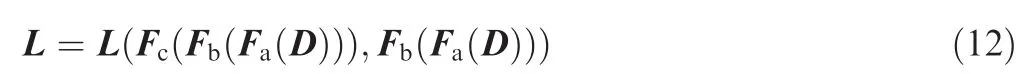
To utilize gradient-based optimization methods,the gradient of the objective function with respect to the design variables is required.Therefore,applying the chain rule to Eq.(12),one has
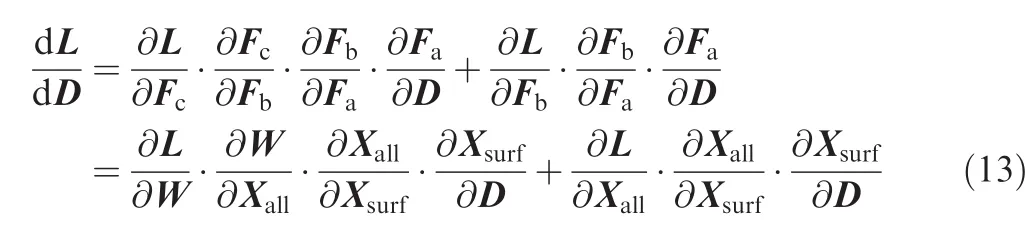
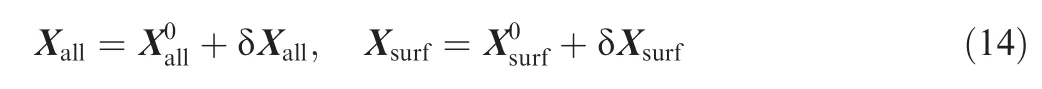


Substituting Eqs.(15)and(17)into Eq.(13),one can obtain the final expression for the gradient of the objective function

Eq.(18)is well-known as tangent model,tangent problem,forward differentiation or direct differentiation.According to Eq.(18),the gradient can be calculated in the following steps:
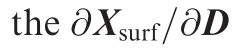
(2)Calculate the mesh sensitivities through the expression

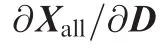
(3)Obtain the flow residual sensitivities using matrix-matrix product(or matrix-vector product in the case of single design variable)

(4)Compute the flow variable sensitivities through the expression

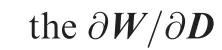
(5)Compute the gradient of the objective function using
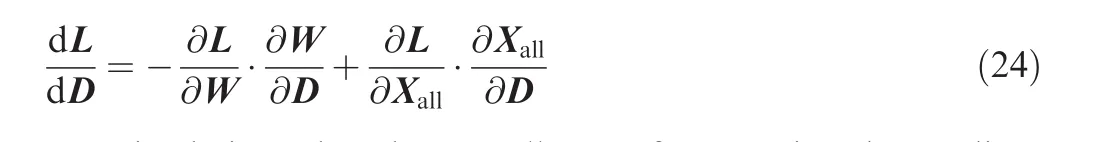
It is obvious that the overall cost of computing the gradient through the tangent model is nearly equal tonDtimes the mesh deformation plusnDtimes the flow solution,scaling linearly with the number of the design variables.Hence the tangent model is usually impractical for optimization problems involving a large number of design variables.
Based on the definition of discrete adjoint,the adjoint model can be obtained by applying transpose operation to the tangent model given by Eq.(18),which yields

According to Eq.(25),the gradient can be calculated in the following steps:
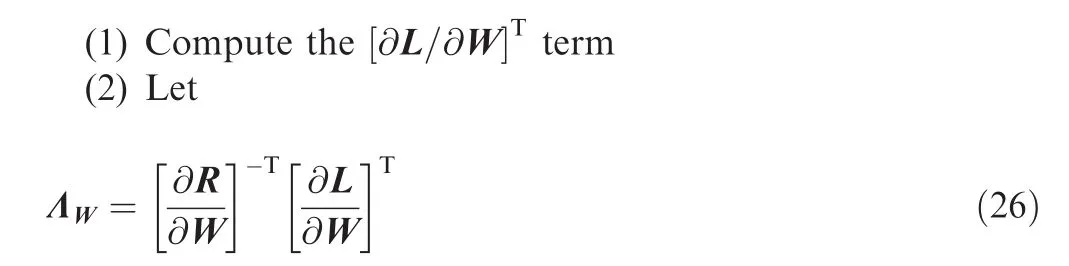

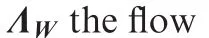
(3)Compute the term

Then Kxis obtained by solving

Eq.(30)represents the mesh adjoint equations and Kxmesh adjoint variables.Since no design variable is involved in Eq.(30),the computational cost of solving Eq.(30)is also independent of the number of the design variables.
(5)Compute the gradient using

Often,the computational cost in this step is relatively low.
Compared to the tangent model,the adjoint model can calculate the gradient at the expense of one flow adjoint solution and one mesh adjoint solution,regardless of the number of the design variables.For this reason,the adjoint model is very eff icient for large-scale optimization problems.
2.3.Detailed formulations of matrix-vector products
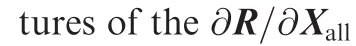
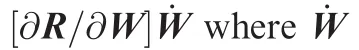
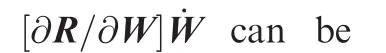
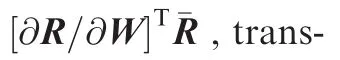
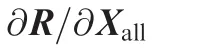

Procedure 1.Complete computational procedure for flow residuals.W Conservative variables and S-A working variables Xall mesh point coordinates v ? F1eXallT !volume fn ? F2eXallT !face normal bn ? F3eXallT !boundary outward normal dwall ? F4eXallT !distance to solid wall K ? F6eW;fn;bnT !spectral radius C ? F7eWT !pressure sensor D ? F8eWT !undivided Laplacian Fcin ? F9eW;fnT !interior average fluxes Fad ? F10eW;K;C;D;fnT !artificial dissipation Fcbc ? F11eW;bnT !convective boundary conditions Fconv?Fcint Fadt Fcbc !mean-flow convective residuals g ? F12eW;fn;bn;vT !gradients l ? F13eWT !viscosity coefficients Fvin ? F14eW;l;g;Xall;fnT !interior viscous fluxes Fvbc ? F15eW;l;g;Xall;bnT !viscous boundary conditions Fvis?Fvint Fvbc !mean-flow viscous residuals

?

FSAc ? F16eW;fnT !convective term in S-A model FSAd ? F17eW;l;Xall;fnT !diffusive term in S-A model FSAbc ? F18eW;l;Xall;bnT !boundary conditions for S-A model FSAs ? F19eW;l;g;v;dwallT !source term in S-A model R? Rmean RSA? Fconvt Fvis FSA ct FSA dt FSA bct FSAs !flow residuals

Procedure 2.Computational procedure for matrix-vector product?@R=@W?_W._W A given vector which has the same dimension as W_K?@F6@W_W_C?@F7@W_W_D?@F8@W_W_Fcin?@F9@W_W_Fad?@F10@W_W t@F10@K_K t@F10@C_C t@F10@D_D_Fcbc?@F11@W_W_Fconv?_Fcint_Fadt_Fcbc_g?@F12@W_W_l?@F13@W_W_Fvin?@F14@W_W t@F14@l_l t@F14@g_g_Fvbc?@F15@W_W t@F15@l_l t@F15@g_g_Fvis?_Fvint_Fvbc_FSAc?@F16@W_W_FSAd?@F17@W_W t@F17@l_l_FSAbc?@F18@W_W t@F18@l_l_FSAs?@F19@W_W t@F19@l_l t@F19@g_g_R?@R@W_W? _Rmean_RSA? _Fconvt_Fvis_FSA ct_FSA dt_FSA bct_FSAs

?

?

?

?


And the corresponding contributions to the transposed Jacobian can be easily obtained as
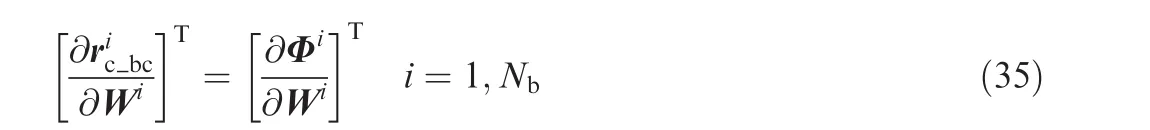
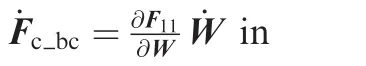
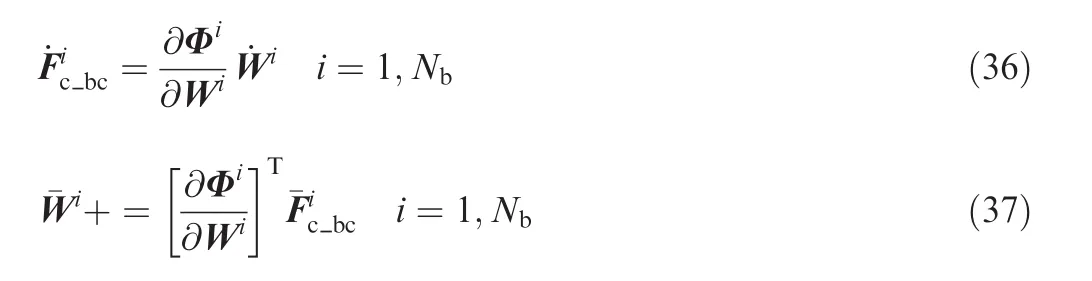
In the current flow solver,all boundary conditions including viscous wall boundary condition are imposed weakly,so all matrix-vector products involving boundary contributions can be performed in a similar manner as Eqs.(36)or(37),without any special treatment for the incorporation of strong boundary condition.35
3.Adjoint implementation
3.1.Basic background of automatic differentiation
Although conceptually simple and straightforward,manual implementation of procedural components for computing each intermediate term in the above procedures usually implies error-prone derivation,large programming efforts and lengthy development time.A viable technique to address this issue is automatic differentiation,which can automatically generate codes for calculating the required matrix-vector products.AD tools usually offer two different modes of operation:the forward(or tangent)mode and the reverse(or adjoint)mode.AD technique can be implemented by two approaches:source transformation and operator overloading.AD tools that use source transformation technique analyze the original source code and add new statements to compute the derivatives of the original statements.Operator overloading defines a new user-defined type which consists of a real number and its derivative to replace the original real type.The details of AD techniques can be found in Ref.14.
In this paper,TAPENADE36is chosen as it is free available on the website37and supports Fortran 90 programming language.Tapenade uses source transformation method to generate codes for computing derivatives and supports both tangent mode and reverse mode.Before the application of Tapenade to the residual computation procedure,a simple example is presented to demonstrate the implications of these two modes.
We consider a vector function F with two input variablesx1,x2
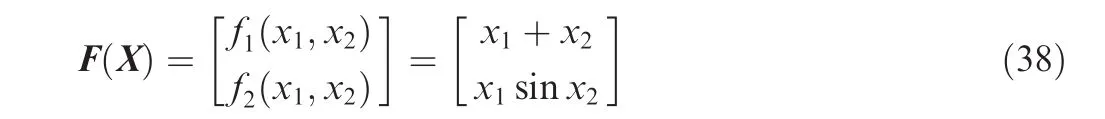
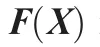

Fig.1 Fortran 90 code of evaluating

Fig.2 Differentiated code generated by tangent mode.
3.2.Implementation of matrix-vector products in tangent and adjoint models

Fig.3 Differentiated code generated by reverse mode.
The clear sturctures of the procedures for matrix-vector products(Procedures 2–5)are beneficial to the application of AD tools in a structured and modular manner.Each intermediate term in the these procedures is corresponding to a specific component in the residual computation,so the detailed routines for evaluating these intermediate terms can be easily generated bytheuseofappropriatemodeofAD tothe corresponding component in the residual computation.

Fig.4 Original code and codes generated by TAPENADE.
4.Solution of tangent and adjoint models
In the tangent model,Eq.(23)represents a linearized flow problem,which implies the solution of linear equations.A viable strategy to solve Eq.(23)is using the same method as the one used for the flow equations.22The first-order backward-Euler time integration for the flow equations can be written as

where Dtrepresents a diagonal matrix that contains local cell volumes divided by local time steps,Wnthe flow variables at time stepnand R the residuals.Linearizing the residuals gives



this method is illustrated in Fig.5.
To exploit the above iterative method for the solution of Eq.(23),applying the algorithm of Eq.(40)to Eq.(23)yields
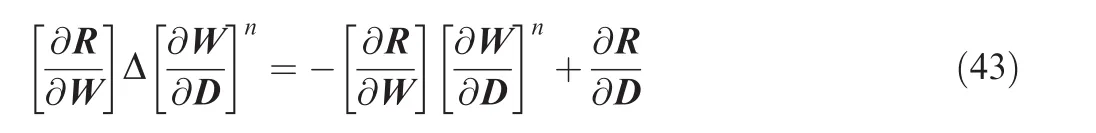
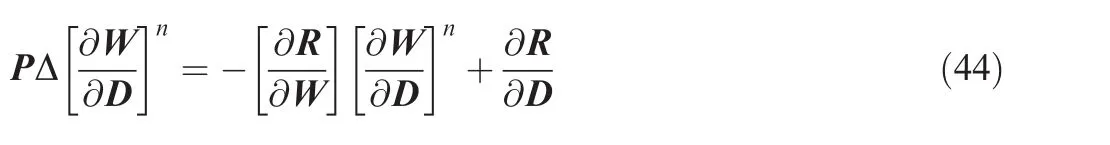

Fig.5 Multicolor Gauss-Seidel method.

Fig.6 Multicolor Gauss-Seidel method for flow adjoint equations.
Accordingly,the solution procedure used for Eq.(41)can be directly applied to Eq.(44).In Eq.(44),the result of the exact Jacobian multiplied by a vector on the right-hand side is computed through the procedures implemented by the forward mode of AD as described in Section 3.Since the same matrix P is used,the convergence of Eq.(44)is guaranteed,provided the flow solution is converged.
In the adjoint model,the flow adjoint equations given by Eq.(27)also imply the solution of linear equations.In this paper,exact adjoint of the above iterative algorithm,often referred to as duality-preserving iteration21,22,is developed and can be written as
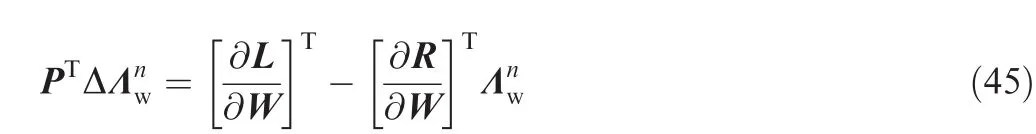

To solve Eq.(46),multicolor Gauss-Seidel method is also employed.However,due to the transpose operation,the loop over colors is reversed(Fig.6).
This iterative algorithm guarantees that the convergence rate is identical with that of the tangent model since the transposed matrix PThas the same eigenvalues as the matrix P.Accordingly,the results computed by the tangent model and the adjoint model are consistent in the sense of machine precision through each iteration.
In addition to the linearized flow equations and the flow adjoint equations given by Eqs.(23)and(27)respectively,the tangent model requires the solution of the mesh tangent problem given by Eq.(20),and the adjoint model requires the solution of the mesh adjoint problem given by Eq.(30).In this paper,linear elasticity analogy method is adopted for mesh deformation.28The mesh is assumed as an elastic solid governed by the equations of linear elasticity which can be written as

where r represents the stress tensor and f some body force.r is related to the strain tensor e by the constitutive relation

whereTrrepresents the trace,and k and l represent the Lame′parameters which can be given in terms of Young’s modulusEand Poisson’s ratio m as
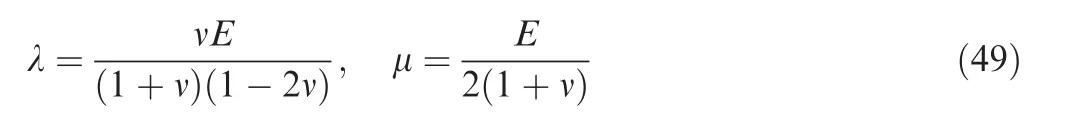
The strain stress e can be expressed in terms of displacements u as

On the boundaries,the displacements are specified as Dirichlet boundary condition.
Eq.(47)is discretized by the standard finite element method,and body force f is set to zero.Young’s modulusEcan be taken as either inversely to the element volume or inversely proportional to the distance from the nearest solid boundary and Poisson’s ratio m is set to a constant value ranging between?1.0 and 0.5.40The resulting linear equations,given by Eq.(8),are solved using block ILU(k)preconditioned flexible generalized minimal residual(FGMRES)method.41
The mesh tangent problem given by Eq.(20)and the mesh adjoint equations given by Eq.(30)are both solved using the same method,since the stiff matrix in Eq.(20)is identical with that in Eq.(8)and the matrix in Eq.(30)is the transposed one.It should be noted that although the current preconditioned FGMRES method used to solve the mesh adjoint equations is not implemented as a duality-preserving iterative algorithm,the global duality between the tangent and adjoint model is preserved,provided convergences to machine precision are achieved for both mesh tangent and adjoint problems,as will be shown in the following section.
Fig.7 Wing surface mesh and location of specific FFD control point.
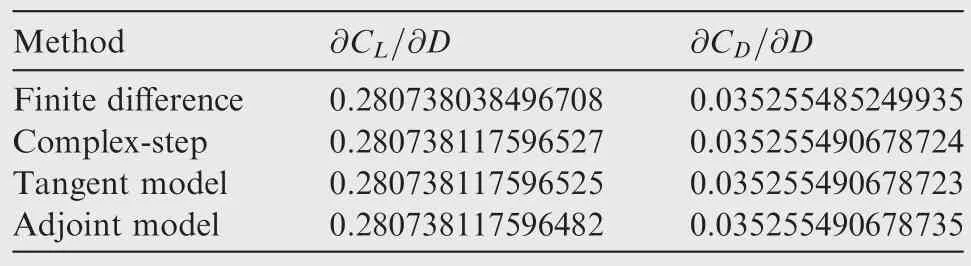
Table 1 Derivative verification.
5.Verification
To verify the gradients obtained by the proposed method,a three-step strategy is adopted,as depicted in the following:
(1)The complex-step method is developed for the entire optimization problem.The complex-step method is an accurate and robust derivative approximation method and has been applied to exact linearizations of complicated real-valued residual operators.42For a realvalued function fexT,if the input becomes a complex value x t ih,where h is a small step size,the Taylor series of the function fex t ihT can be written as

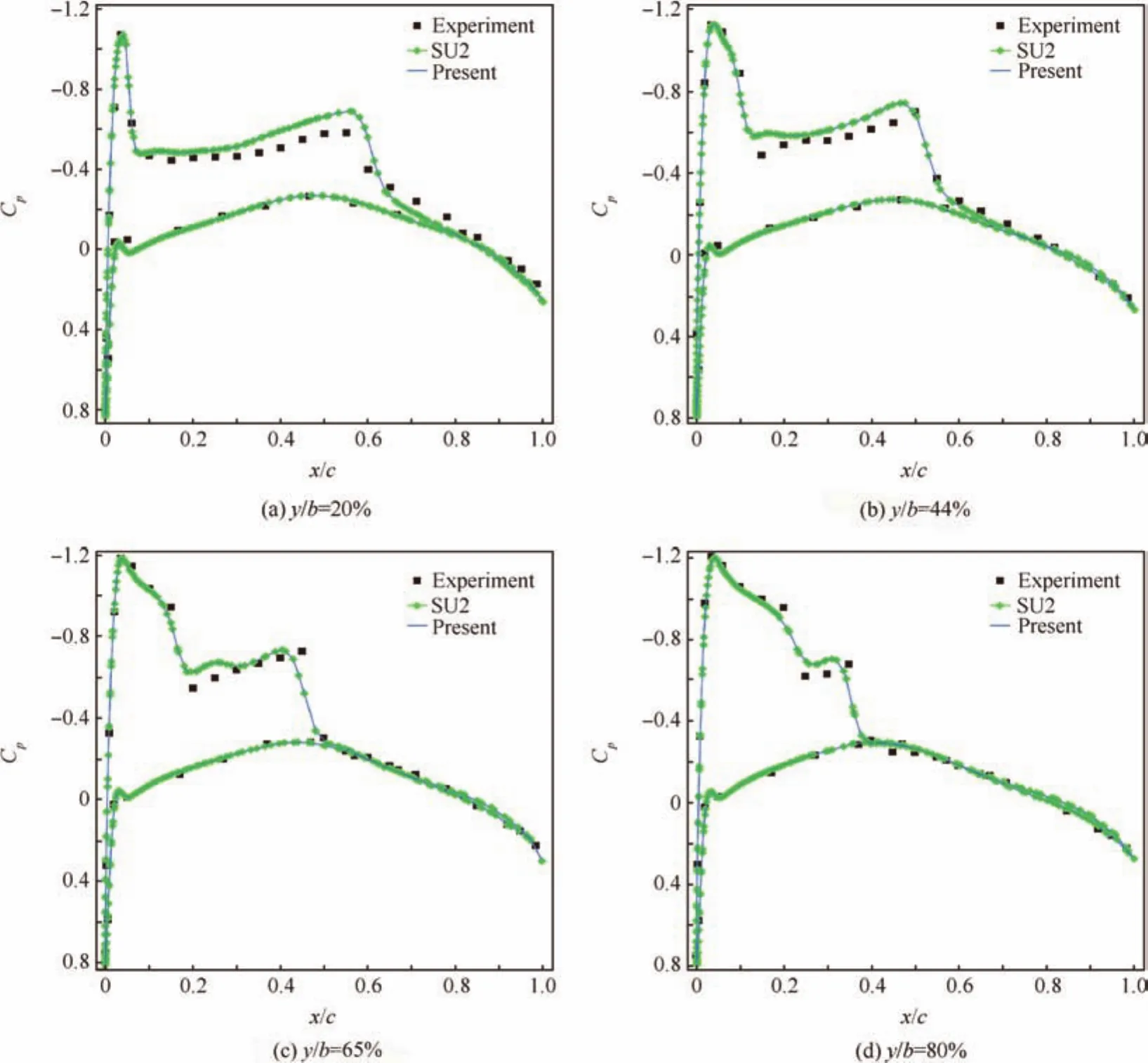
Fig.8 Pressure coefficient distributions at different spanwise sections for ONERA M6 wing.
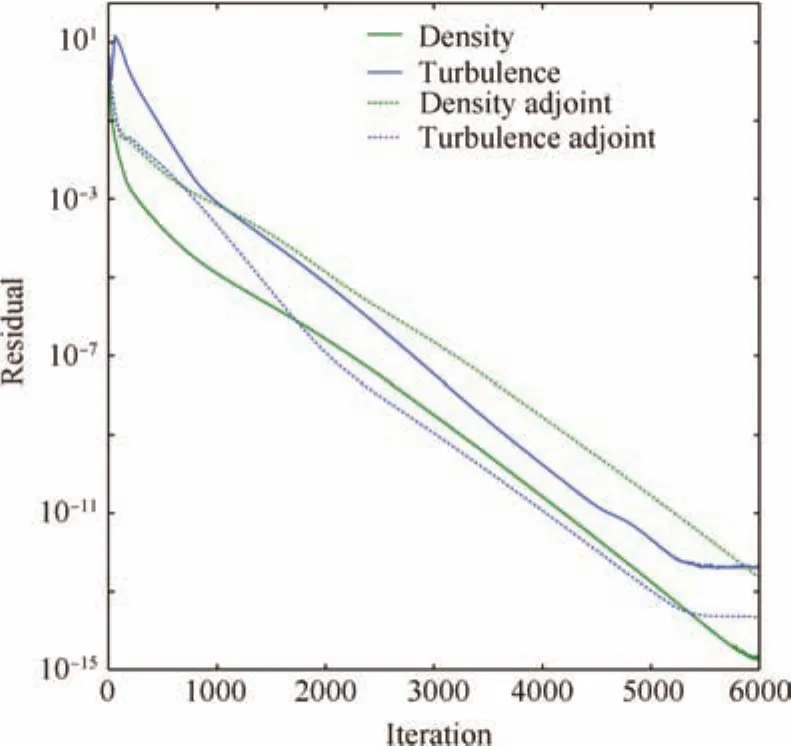
Fig.9 Convergence histories for flow solution and flow adjoint solution.

Table 3 Computational time of flow adjoint solution and flow solution.
Fig.10 Surface mesh and FFD box for DLR-F6 wing-body configuration.

?
where Im represents imaginary part.This approximation is second-order accurate with no differencing involved,avoiding the ‘step-size dilemma”.11So this method can provide a very accurate derivative approximation,if a small enough step size is given.The implementation of the complex-step method in Fortran 90 codes is mostly automated with the help of a Python script and a module provided by Martins et al.11The derivative obtained by the complex-step method can be verified using central finite difference.
(2)The complex-step method is applied to the verification of the implementation of the tangent model.In fact,it has been proven that the complex-step method is equivalent to the tangent model.43This equivalence requires that these two methods should provide identical result for each individual component as well as each iteration within machine precision.Thus,procedural components generated by the forward mode of AD can be first veri-fied with the corresponding parts of the complex-step method and then the results in each iteration are compared to check the correctness of the complete tangent model.
(3)The adjoint computation is verified by checking the duality between the tangent and adjoint models.Any procedural component for matrix-vector product in the tangent model can be written as

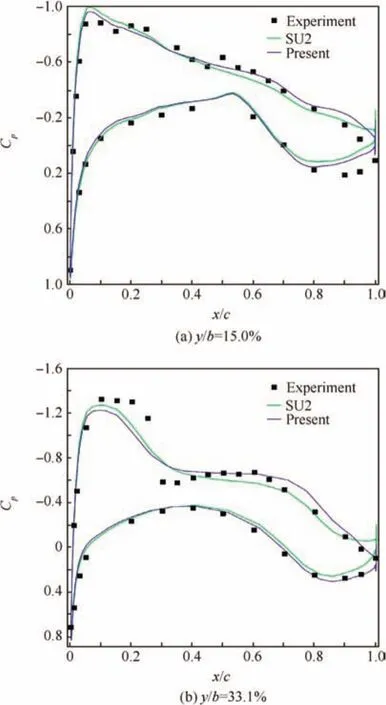
Fig.11 Pressure coefficient distributions at different spanwise sections for DLR-F6 wing-body configuration.
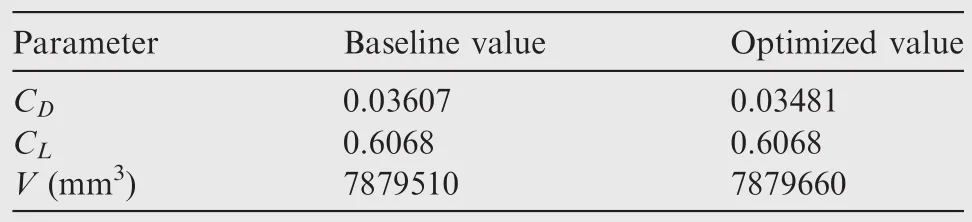
Table 4 Optimization result.
where_x represents input vector and_y output vector.The corresponding procedural component for matrix-vector product in the adjoint model can be written as

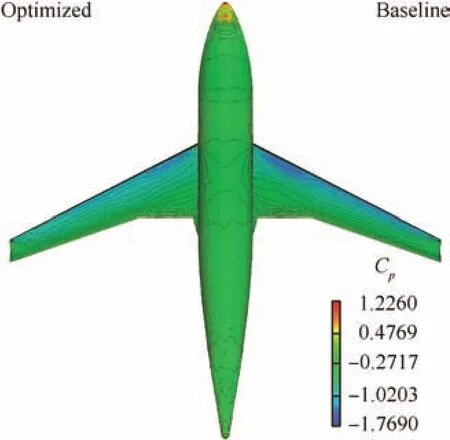
Fig.12 Upper surface pressure coefficient contours of optimized and baseline configurations.


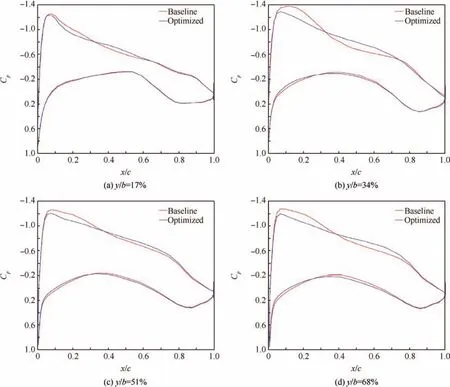
Fig.13 Comparison of baseline and optimized pressure coefficient distributions at different sections along spanwise direction.
First,the results of the flow solution are compared with the experimental data45and the results computed by the opensource CFD solver SU2 on the same mesh.The pressure coefficientCpdistributions at different sections along the spanwise direction are shown in Fig.8.The present results nearly coincide with the results of SU2 solver,since the current flow solver uses the identical implementation for convective flux.And the present results also demonstrate good agreement with the experimental data.
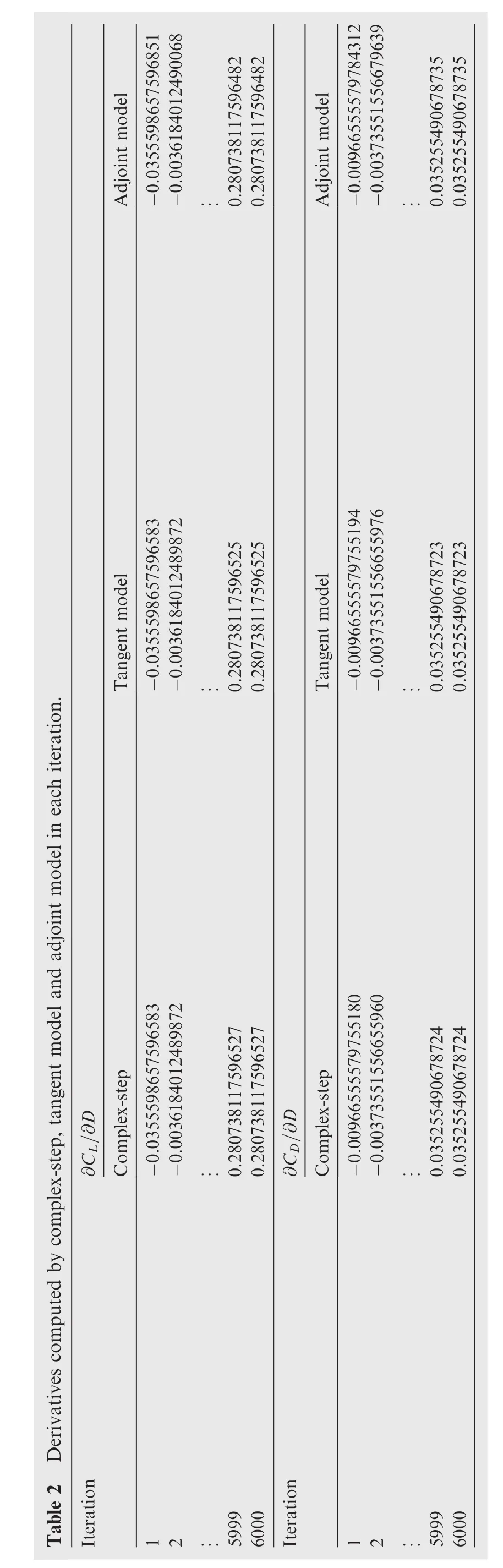
For the veri fication of the derivatives,the finite difference step size is set to 10?6and the complex-step size is set to 10?30.The final derivatives obtained by four methods are shown in Table 1.The derivatives computed by the adjoint model yield agreements of 12 signi ficant figures when compared to the results of the complex-step method and the tangent model,and agreements of 6 significant figures when compared to the results of the finite difference method.It is evident that the obtained derivatives are highly accurate for the gradient based optimization process.The derivatives computed by the complex-step method,the tangent model and the adjoint model in each iteration are shown in Table 2 to indicate the equivalence of the complex-step method and the tangentmodeland theduality-preservingpropertyofthe proposed adjoint implementation.Fig.9 shows the convergence histories for the flow solution and the flow adjoint solution.As expected,the convergences of the flow equations and flow adjoint equations exhibit similar asymptotic rates,since duality-preserving iteration is used.The computational time for a single flow adjoint solution and a single flow solution and the ratio are shown in Table 3.A single flow adjoint computation only costs 7%more time than a single flow solution.This indicates that the proposed method can provide comparable performance to hand-coded implementation,meanwhile avoiding the drawback of tedious and error-prone manual derivation and programming ofdetailed computational procedures.
6.Optimization results
Based on the methodology described previously,a gradientbased optimization framework has been developed and applied to aerodynamic design optimization problem of the DLR-F6 wing-body configuration.This optimization problem consists of minimizing the drag coefficient meanwhile holding the lift coefficient and the wing volume not less than the baseline values,which can be formulated as


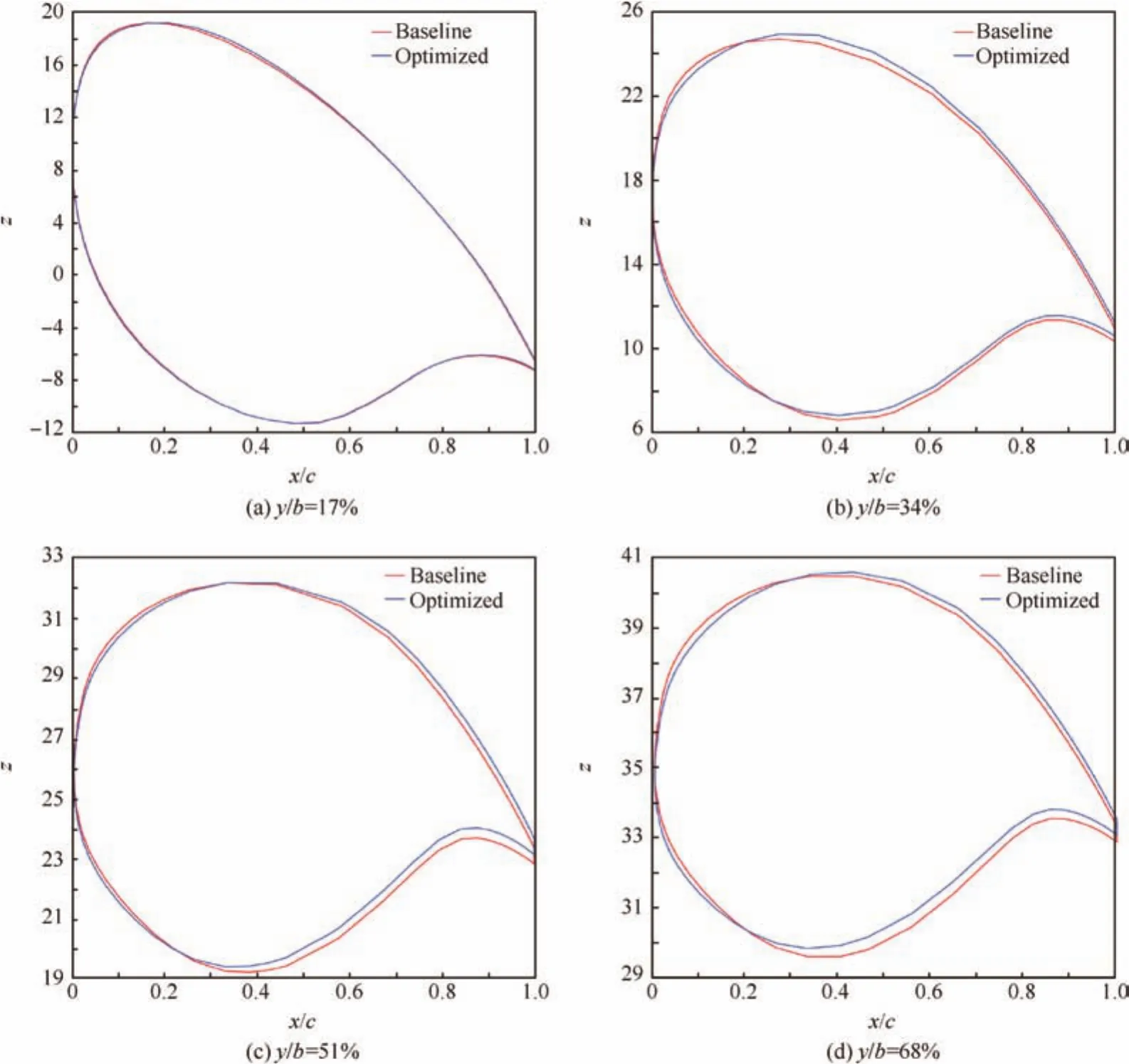
Fig.14 Comparison of baseline and optimized airfoil shapes at different sections along spanwise direction.
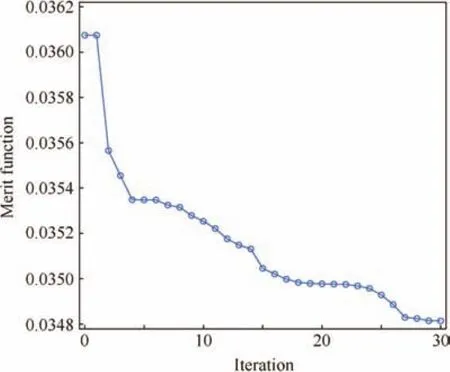
Fig.15 Convergence history for optimization problem.

7.Conclusions
A systematic methodology for developing efficient and accurate discrete adjoint solver on unstructured meshes has been presented.The application of AD tools in a structured and modular manner avoids tedious and error-prone manual derivation and programming of detailed computational procedures for the adjoint model involved in hand-coded implementation,meanwhile provides comparable efficiency.The dualitypreserving adjoint implementation and iterative algorithm used for the solution of flow adjoint equations guarantee that the resulting gradient is consistent with the one calculated by the tangent model and the complex-step method in the sense of machine precision and highly accurate.Future work will focus on the extension of the proposed approach to sensitivity analysis and aerodynamic shape optimization of incompressible flows.48The development of more effective optimization algorithm for realistic problems,e.g.one-shot method,49will also be considered.
Acknowledgements
This study was supported by the Priority Academic Program Development of Jiangsu Higher Education Institutions of China.
1.Jameson A.Aerodynamic design via control theory.J Sci Comput1988;3(3):233–60.
2.Anderson WK,Venkatakrishnan V.Aerodynamic design optimization on unstructured grids with a continuous adjoint formulation.Reston:AIAA;1997.Report No.:AIAA-1997-0643.
3.Castro C,Lozano C,Palacios F,Zuazua E.A systematic continuous adjoint approach to viscous aerodynamic design on unstructured grids.Reston:AIAA;2006.Report No.:AIAA-2006-0051.
4.Bueno-Orovio A,Castro C,Palacios F,Zuazua E.Continuous adjoint approach for the Spalart-Allmaras model in aerodynamic optimization.Reston:AIAA;2011.Report No.:AIAA-2011-1299.
5.Zymaris AS,Paradimitriou DI,Giannkoglou KC,Othmer C.Continuous adjoint approach to the Spalart-Allmaras turbulence model for incompressible flows.ComputFluids2009;38(8):1528–38.
6.Nielsen EJ,Anderson WK.Recent improvements in aerodynamic optimization on unstructured meshes.AIAA J2002;40(6):1155–63.
7.Elliot J,Peraire J.Practical three-dimensional aerodynamic design and optimization using unstructured meshes.AIAA J1997;35(9):1479–85.
8.Kim HJ,Sasaki D,Obayashi S,Nakahashi K.Aerodynamic optimization of supersonic transport wing using unstructured adjoint method.AIAA J2001;39(6):1011–20.
9.Nadarajah SK.The discrete adjoint approach to aerodynamic shape optimization [dissertation].Stanford (USA):Stanford University;2003.
10.Carpentieri G.An adjoint-based shape-optimization method for aerodynamic design [dissertation].Delft(Netherlands):Delft University of Technology;2009.
11.Martins JRRA,Sturdza P,Alonso JJ.The complex-step derivative approximation.ACM Trans Math Software2003;29(3):245–62.
12.Yu W,Blair M.DNAD,a simple tool for automatic differentiation of Fortran codes using dual numbers.Comput Phys Commun2013;184(5):1446–52.
13.Dwight RP,Brezillon J.Effect of approximations of the discrete adjointon gradient-based optimization.AIAAJ2006;44(12):3022–31.
14.Griewank A,Walther A.Evaluating derivatives:principles and techniques of algorithmic differentiation.2nd ed.Philadelphia:Society for Industrial and Applied Mathematics;2008.
15.Giles MB,Ghate D,Duta MC.Using automatic differentiation for adjoint CFD code development.Oxford:Oxford University Computing Laboratory;2005.Report No.:NA-05/25.
16.Mader CA,Martins JRRA,Alonso JJ,van der Weide E.ADjoint:an approach for the rapid development of discrete adjoint solvers.AIAA J2008;46(4):863–73.
17.Christakopoulos F,Jones D,Mu¨ller JD.Pseudo-timestepping and verification for automatic differentiation derived CFD codes.Comput Fluids2011;46(1):174–9.
18.Lyu Z,Kenway GKW,Paige C,Martins JRRA.Automatic differentiation adjoint of the Reynolds-Averaged Navier-Stokes equations with a turbulence model.Reston:AIAA;2013.Report No.:AIAA-2013-2581.
19.Biava M,Woodgate M,Barakos GN.Fully implicit discreteadjoint methods for rotorcraft applications.AIAA J2016;54(2):735–49.
20.Mavriplis DJ.Discrete adjoint-based approach for optimization problems on three-dimensional unstructured meshes.AIAA J2007;45(4):740–50.
21.Dwight RP,Brezillon J.Efficient and robust algorithms for solution of the adjoint compressible Navier-Stokes equations with applications.Int J Numer Meth Fluids2009;60(4):365–89.
22.Nielsen EJ,Lu J,Park MA,Darmofal DL.An implicit,exact dual adjoint solution method for turbulent flows on unstructured grids.Comput Fluids2004;33(9):1131–55.
23.Economon TD,Palacios F,Copeland SR,Lukaczyk TW,Alonso JJ.SU2:an open-source suite for multiphysics simulation and design.AIAA J2016;54(3):828–46.
24.Albring T,Sagebaum M,Gauger NR.Efficient aerodynamic design using the discrete adjoint method in SU2.Reston:AIAA;2016.Report No.:AIAA-2016-3518.
25.Auvinen MJS.A modular framework for generation and maintenance of adjoint solvers assisted by algorithmic differentiation[dissertation].Helsinki(Finland):Aalto University;2014.
26.Giles MB,Pierce NA.An introduction to the adjoint approach to design.Flow Turbul Combust2000;65(3):393–415.
27.Batina JT.Unsteady Euler airfoil solution using unstructured dynamic meshes.AIAA J1990;28(8):1381–8.
28.Dwight R.Robust mesh deformation using the linear elasticity equations.In:Deconinck H,Dick E,editors.Computational fluid dynamics 2006:proceedings of the fourth international conference on computational fluid dynamics.Berlin:Springer;2009.p.401–6.29.Amoignon O.Adjoint of a median-dual finite-volume scheme:application to transonic aerodynamic shape optimization.Uppsala:Uppsala University;2006.Report No.:Technical Report 2006–013.
30.Jameson A,Schmidt W,Turkel E.Numerical solution of the Euler equations by finite volume methods using Runge-Kutta timestepping schemes.Reston:AIAA;1981.Report No.:AIAA-1981-1259.
31.Haselbacher A,Blazek J.Accurate and efficient discretization of Navier-Stokesequationsonmixed grids.AIAAJ2000;38(11):2094–102.
32.Thomas JL,Diskin B,Nishikawa H.A critical study of agglomerated multigrid methods for diffusion on highly-stretched grids.Comput Fluids2011;41(1):82–93.
33.Stuck A.An adjoint view on flux consistency and strong wall boundary conditions to the Navier-Stokes equations.J Comput Phys2015;301:247–64.
34.Spalart P,Allmaras S.A one-equation turbulence model for aerodynamic flows.Reston:AIAA;1992.Report No.:AIAA-1992-0439.
35.Giles MB,Duta MC,Mu¨ller JD,Pierce NA.Algorithm developments for discrete adjoint methods.AIAA J2003;41(2):198–205.
36.Hascoet L,Pascual V.The Tapenade automatic differentiation tool:principles,model,and specification.ACM Trans Math Software2013;39(3):1–43.
37.TAPENADE[Internet].[cited 2016 Jun 4].Available from:http://www-tapenade.inria.fr:8080/tapenade/index.jsp.
38.Koren B.Defect correction and multigrid for an efficient and accurate computation of airfoil flows.J Comput Phys1988;77(1):183–206.
39.Sato Y,Hino T,Ohashi K.Parallelization of an unstructured Navier-Stokes solver using a multi-color ordering method for OpenMP.Comput Fluids2013;88:496–509.
40.Yang Z,Mavriplis DJ.Unstructured dynamic meshes with higherorder time integration schemes for the unsteady Navier-Stokes equations.Reston:AIAA;2005.Report No.:AIAA-2005-1222.
41.Saad Y.Iterativemethodsforsparselinearsystems.2nd ed.Philadelphia:Society for Industrial and Applied Mathematics;2003.
42.Nielsen E,Kleb W.Efficient construction of discrete adjoint operators on unstructured grids using complex variables.AIAA J2006;44(4):827–36.
43.Martins J,Sturdza P,Alonso J.The connection between the complex-step derivative approximation and algorithmic differentiation.Reston:AIAA;2001.Report No.:AIAA-2001-0921.
44.Sederberg T,Parry S.Free-form deformation of solid geometric models.Comp Graph1986;20(4):151–60.
45.Schmitt V,Charpin F.Pressure distributions on the ONERA-M6-Wing at transonic Mach number.Paris:AGARD;1979.Report No.:AGARD AR 138.
46.2nd AIAA CFD Drag Prediction Workshop[Internet].[cited 2016 Jun 4].Availablefrom:https://aiaa-dpw.larc.nasa.gov/Workshop2/workshop2.html.
47.Gill PE,Murray W,Saunders MA,Wright MH.User’s guide for NPSOL 5.0:a Fortran package for nonlinear programming.California:SOL;1986.Report No.:Technical Report SOL 86–1.
48.Liu Q,Go′mez F,Pe′rez JM,Theofilis V.Instability and sensitivity analysis of flows using OpenFOAM?.Chin J Aeronaut2016;29(2):316–25.
49.Gu¨nther S,Gauger NR,Wang Q.Simultaneous single-step oneshot optimization with unsteady PDEs.J Comput Appl Math2016;294:12–22.
4 July 2016;revised 1 September 2016;accepted 30 November 2016
Available online 14 February 2017
*Corresponding author.
E-mail addresses:gaoyisheng@nuaa.edu.cn(Y.Gao),wyzao@nuaa.edu.cn(Y.Wu),jxia@nuaa.edu.cn(J.Xia).
Peer review under responsibility of Editorial Committee of CJA.
 CHINESE JOURNAL OF AERONAUTICS2017年2期
CHINESE JOURNAL OF AERONAUTICS2017年2期
- CHINESE JOURNAL OF AERONAUTICS的其它文章
- High-temperature tribological behaviors of a Cr-Si co-alloyed layer on TA15 alloy
- Analysis and control of the compaction force in the composite prepreg tape winding process for rocket motor nozzles
- Impact of lubricant traction coefficient on cage’s dynamic characteristics in high-speed angular contact ball bearing
- Variable stiffness design of redundantly actuated planar rotational parallel mechanisms
- Adaptive formation control of quadrotor unmanned aerial vehicles with bounded control thrust
- Constrained adaptive neural network control of an MIMO aeroelastic system with input nonlinearities
