Solitary Potential in a Space Plasma Containing Dynamical Heavy Ions and Bi-Kappa Distributed Electrons of Two Distinct Temperatures
M.Sarker,B.Hosen,M.R.Hossen,and A.A.Mamun
1Department of Physics,Jahangirnagar University,Savar,Dhaka-1342,Bangladesh
2Department of General Educational Development,Daffodil International University,Dhanmondi,Dhaka-1207,Bangladesh
1 Introduction
The propagation of ion-acoustic waves[1?4]in electronion(EI)plasmas has received a great deal of renewed interest because of their vital role in understanding different kinds of nonlinear electrostatic structures(viz.solitary waves,shock structures,double layers,etc.[5?18])observed in space[19?21]and laboratory devices.[22?24]The existence of heavy ions in astrophysical plasmas has been con firmed experimentally by detecting a noble gas molecular heavy ion in the crab nebula,[25]our(Milky Way)Galaxy,[26]polar region of neutron stars,[27]active galactic nuclei,[28]pulsar magnetosphere,[29]and the early universe,[30]etc.
The particle distribution near equilibrium is often considered to be Maxwellian for the modeling of different plasma systems.However,for many space plasma environments,it has been proven that the presence of the heavy ion and electron populations are far o fffrom their thermal equilibrium state.The effects of external forces or wave particle interaction in numerous space[31?32]and laboratory[33?34]plasma situations indicate the existence of highly energetic(super-thermal)particles.The existence of accelerated,energetic(super-thermal)particles in the measurement of electron distribution in near-Earth space environments[32,35?36]suggests a signi ficant deviation from Maxwellian equilibrium.So for a proper treatment of a plasma system with super-thermal electrons,one should not consider Maxwellian distribution function(DF),but other kind of non-Maxwellian DF like super thermal(κ)DF.[37?39]The latter is given by
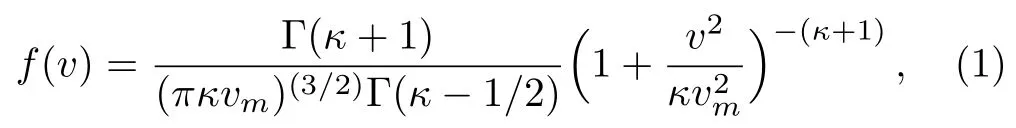
where Γ is the usual gamma function;is the most probable speed of the high energetic electron species withbeing the Boltzman constant,Tebeing the characteristic kinetic temperature of electron species,andmebeing the mass of an electron;κis the spectral index,[40?41]which measures the deviation from the Maxwellian electron distribution.We note thatκ=∞corresponds to the Maxwellian electron distribution,and that asκdecreases within a rangethe deviation from the Maxwellian electron distribution increases.
Recently, a numerousinvestigationshave been made by many authors on ion-acoustic solitary waves(IASWs)with single-temperature super-thermal(kappa distributed)electrons.[44?46]Schipperset al.[47]have combined a hot and a cold electron component,while both electrons are kappa distributed and a best fit for the electron velocity distribution is found.Balukuet al.[48]used this model for the study of ion-acoustic solitons in a plasma with two-temperature kappa distributed electrons.Pakzad[49]studied a dissipative plasma system with superthermal electrons and positrons,and found that the effects of ion kinematic viscosity and the super-thermal parameter on the ion-acoustic shock waves.Tasnimet al.[50?51]also considered two-temperature non-thermal ions,and discussed the properties of dust-acoustic solitary waves and double layers. Masudet al.[52]have studied the characteristics of DIA shock waves in an unmagnetized dusty plasma consisting of negatively charged static dust,inertial ions,Maxwellian distributed positively charged positrons,and super-thermal electrons with two distinct temperatures.Luet al.[53]have examined the electronacoustic waves in an electron-beam plasma system containing cold and hot electrons.El-Taibanyet al.[54]have made stability analysis of dust-ion acoustic solitary waves in a magnetized multicomponent dusty plasma containing negative heavy ions and stationary variable-charge dust particles.Shahmansouri[55]investigated the basic properties of ion-acoustic waves in an unmagnetized plasma containing cold and hot ions with kappa distributed electrons.Emaet al.[56?57]studied the effects of adiabacity on the heavy ion acoustic(HIA)solitary and shock waves in a strongly coupled nonextensive plasma.They observed that the roles of the adiabatic positively charged heavy ions,and nonextensivity of electrons have significantly modi fied the basic features(viz.polarity,amplitude,width,etc.) of the HIA solitary/shock waves.Hossenet al.[58?60]considered positively charged static heavy ions in a relativistic degenerate plasma and rigorously investigated the basic features of solitary and shock structures.Shahet al.[61?62]investigated the basic features of HIA solitary and shock waves by considering both planar and nonplanar geometry.
We expect that dynamical heavy particles and higher order nonlinearity play an important role in modifying the basic non-linear features of ion-acoustic waves propagating in space and laboratory plasmas.Therefore,our main objective in this work is to investigate the effects of dynamics of heavy ions and higher non-linearity on(HIAWs)by deriving Korteweg-de Vries(K-dV),modi fied K-dV(MK-dV)equation,and higher order MK-dV(HMK-dV)and also is to consider the dynamics of heavy particles to describe heavy ion acoustic solitary waves(HIASWs)in such plasma system under consideration.
The manuscript is organized as follows.The basic equations are provided in Sec.2.Three different types of nonlinear equations,namely K-dV,MK-dV,and HMK-dV are derived and analyzed analytically and numerically in Sec.3.A brief discussion is finally presented in Sec.4.
2 Basic Equations
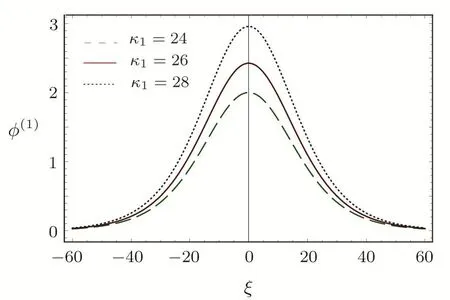
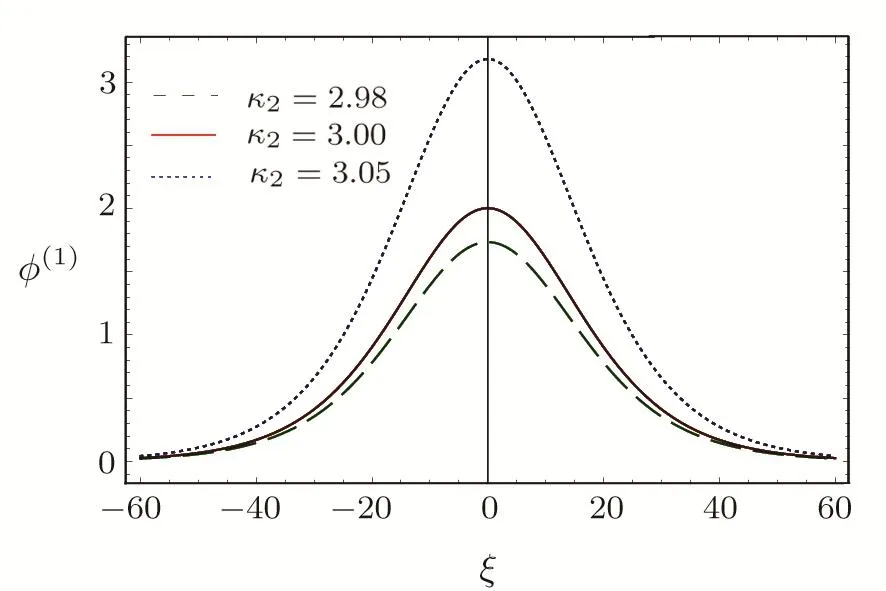
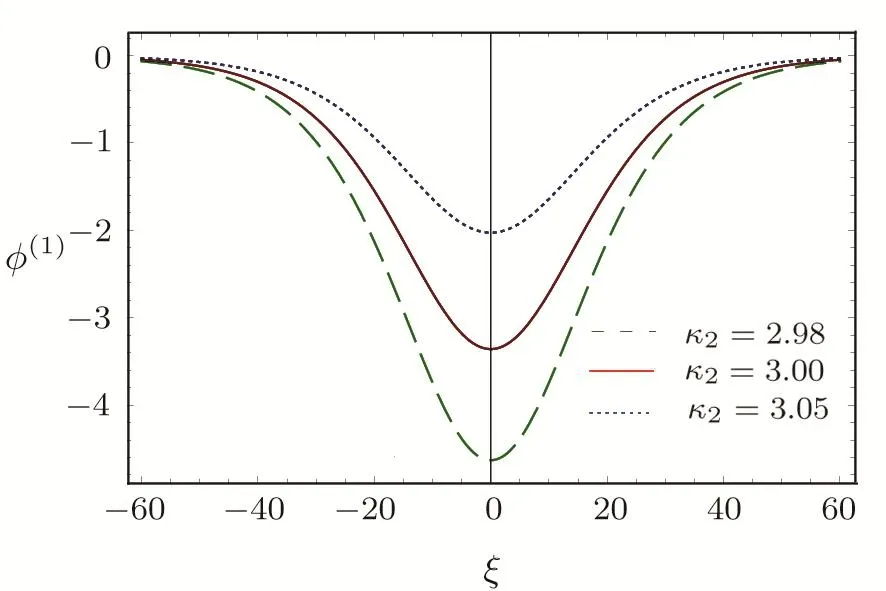
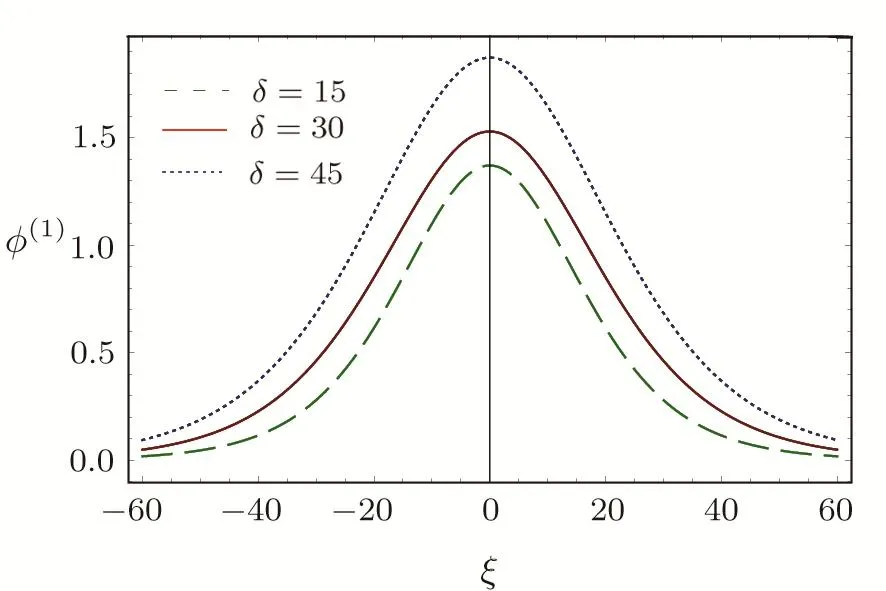
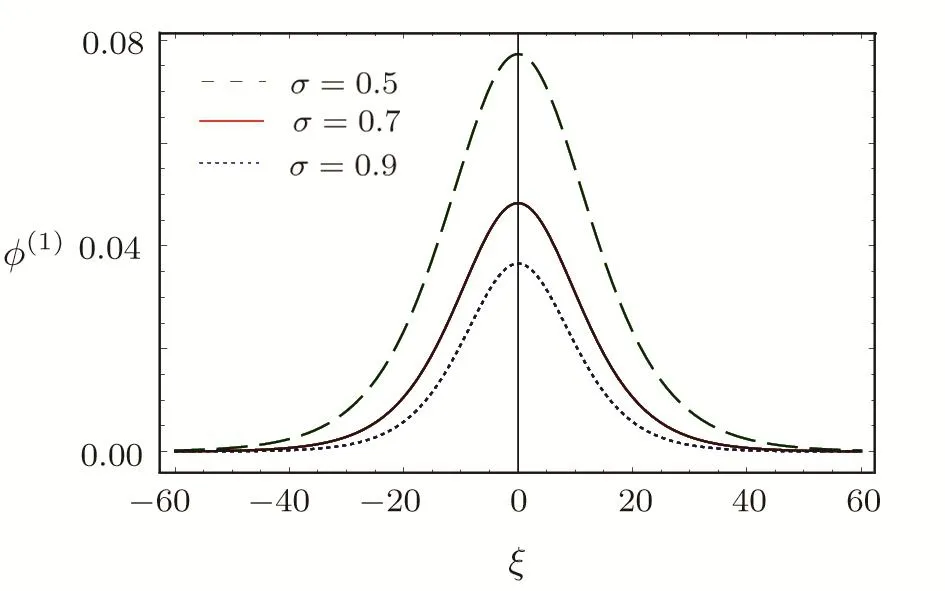
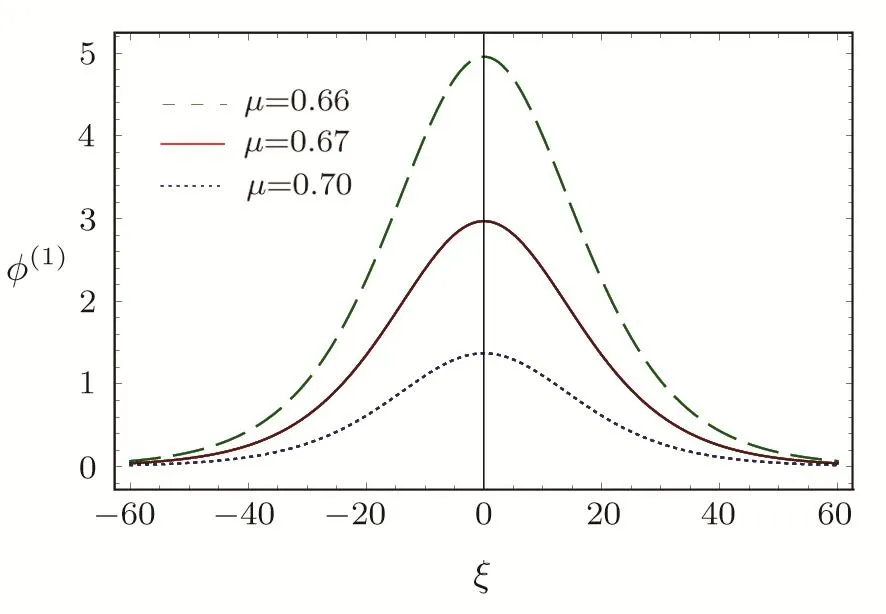
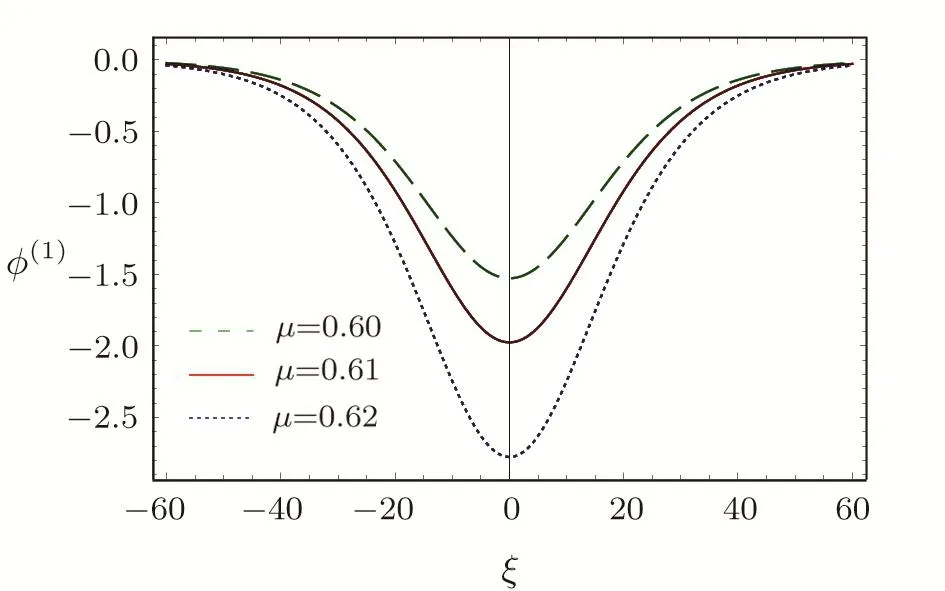
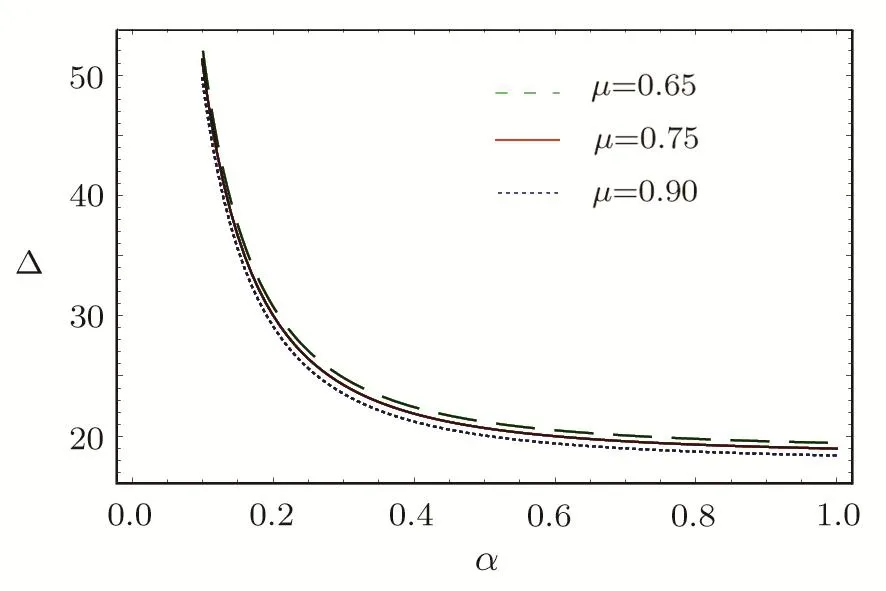
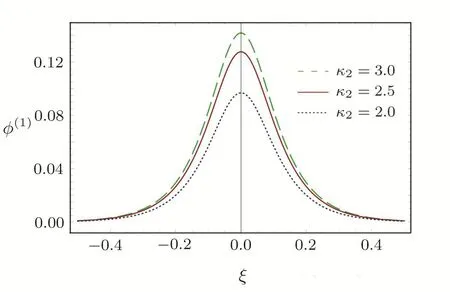
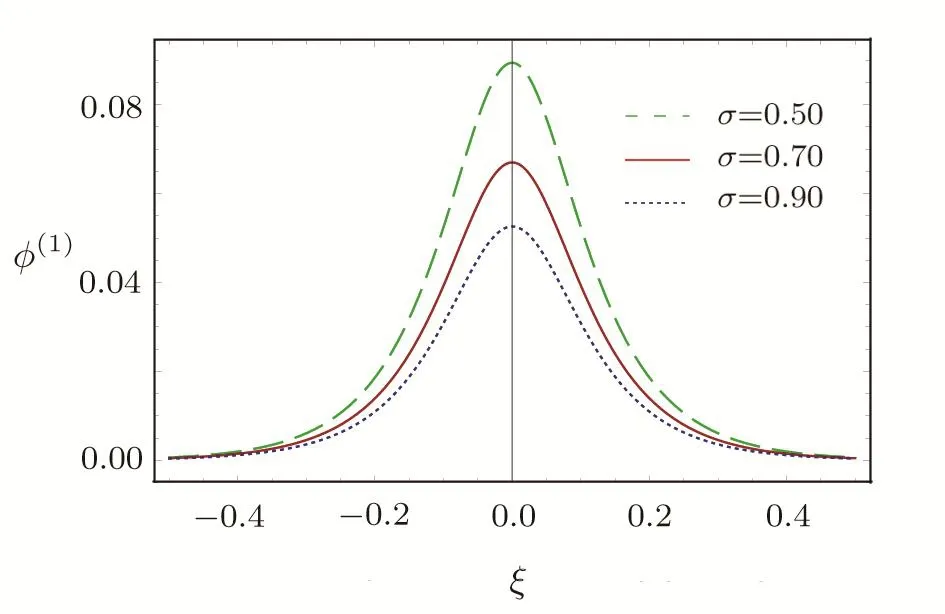
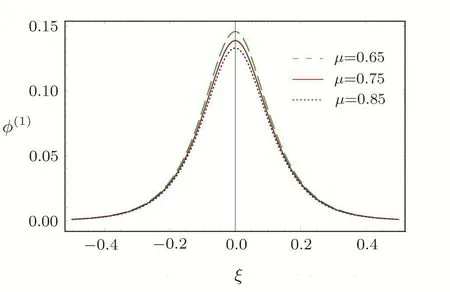
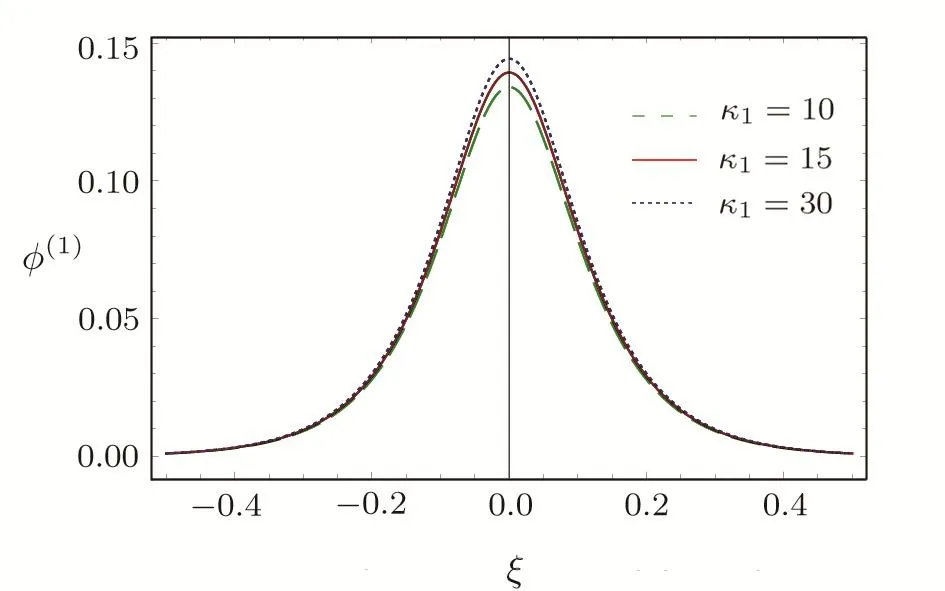
We consider a three component magnetized plasma system containing positively charged heavy ions and kappa distributed electrons with two distinct temperaturesT1andT2(T1 wherenhis the heavy ion number density normalized bynh0;uhis the heavy ion fluid speed normalized by(withkBbeing the Boltzmann constant,andmhbeing the heavy ion mass);?is the electrostatic wave potential normalized bykBT1/e(withebeing the magnitude of the charge of an electron);α=(withωch=ZheB0/mhcbeing the heavy ioncyclotron frequency,B0being the magnitude of the external static magnetic field,andbeing the heavy ion plasma frequency);1=1/(1+μ),andis the number density of low(high)temperature electron species;time variable is normalized byand the space variable is normalized by.We note that the external magnetic fieldB0is acting along thez-direction(i.e.,wherez? is the unit vector along thezdirection). The normalized cold and hot electron number densitiesn1andn2are,respectively given by To study nonlinear propagation,we now consider different orders of nonlinearity by deriving and analyzing K-dV,MK-dV,and HMK-dV equations to identify the basic features of HIASWs formed a magnetized space plasma system containing dynamical heavy ions and kappa distributed electrons of two distinct temperatures. To derive the K-dV equation,we use the reductive perturbation method,which lead to the stretched coordinates:[63?64] whereVpis the phase speed of the HIAWs,?is a smallness parameter measuring the weakness of the dispersion(0 Now,substituting Eqs.(7)–(12)into Eqs.(2)–(4),and then taking the terms containing?3/2from Eqs.(2)and(3),and?from Eq.(4),we obtain We note that Eq.(17)describes the linear dispersion relation for the propagation of the HIAWs in the magnetized plasma under consideration and thatlz=cosδ(whereδis the angle between the directions of external magnetic field and wave propagation).To the next higher order of?,we again substitute Eqs.(7)–(12)into Eqs.(2),z-component of Eq.(3),and Eq.(4)and take the terms containing?5/2from Eq.(2)andz-component of Eq.(3),and?2from Eq.(4).We then use Eqs.(15)–(17)to obtain a set of equations in the form Equation(25)is the K-dV equation describing the nonlinear dynamics of the HIASWs.Now,using the appropriate boundary conditions,viz.?=0,d?/dξ=0,and d2?/dξ2=0 at,the stationary solitary wave solution of Eq.(25)is given by where?m= 3u0/A1is the amplitude,and ? =(4B1/u0)1/2is the width of the HIASWs. To obtain the basic features(viz.polarity,amplitude,and width)of the ESPPs,we have numerically analyzed the solution,Eq.(28)for different plasma situations.The results are displayed in Figs.1–10,which clearly indicate that (i)The ESPPs with?(1)>0(?(1)<0)exist forμ>μc(μ<μc)as shown in Figs.1–4,8,and 9. Fig.1 (Color online)The electrostatic solitary potential pro files(ESPPs)with ?(1)>0 forμ > μc,u0=0.01,σ =0.25,μ =0.7,κ2=3,δ=15,α =0.5,κ1=24(dashed curve),κ1=26(solid curve),and κ1=28(dotted curve). Fig.2 (Color online)The ESPPs with ?(1)<0 forμ < μc,u0=0.01,σ =0.25,μ =0.7,κ2=3,δ=15,α =0.5,κ1=24(dashed curve),κ1=26(solid curve),and κ1=28(dotted curve). (ii)The amplitude and width of the ESPPs(with both?(1)>0 and?(1)<0)increase with the increase inκ1,κ2,andδas shown in Figs.1–5. Fig.3 (Color online)The ESPPs with ?(1)>0 forμ> μc,u0=0.01,σ =0.25,μ=0.7,κ1=24,δ=15,α =0.5,κ2=2.98(dashed curve),κ2=3.00(solid curve),and κ2=3.05(dotted curve). Fig.4 (Color online)The ESPPs with ?(1)<0 forμ< μc,u0=0.01,σ =0.25,μ=0.7,κ1=24,δ=15,α =0.5,κ2=2.98(dashed curve),κ2=3.00(solid curve),and κ2=3.05(dotted curve). Fig.5 (Color online)The ESPPs with ?(1)>0 forμ > μc,u0=0.01,σ =0.25,μ =0.7,κ1=20,κ2=3,α =0.5,δ=15(dashed curve),δ=30(solid curve),and δ=45(dotted curve). (iii)The width of the ESPPs(with?(1)>0)increases(decreases)with the increase inδfor its lower(upper)range,but it decreases with the increase inαas shown in Fig.6;(iv)The amplitude and width of the ESPPs[with?(1)>0]increase with the decrease inσas shown in Fig.7;(v)The amplitude and width of the ESPPs(with both?(1)>0 and?(1)<0)decrease with the increase inμas shown in Figs.8 and 9. (vi)the width of the ESPPs(with?(1)>0)decreases with the increase inμas shown in Fig.10. Fig.6 (Color online)The width of the ESPPs forμ > μc,u0=0.01,σ =0.25,μ =0.7,κ1=20,κ2=3,α =0.5(dashed curve),α =0.6(solid curve),and α=0.7(dotted curve). Fig.7 (Color online)The ESPPs with ?(1)>0 forμ > μc,u0=0.01,δ=15,μ =0.7,κ1=20,κ2=3,α=0.5,σ=0.5(dashed curve),σ=0.7(solid curve),and σ=0.9(dotted curve). Fig.8 (Color online)The ESPPs with ?(1)>0 forμ > μc,u0=0.01,δ=15,σ =0.25,κ1=20,κ2=3,α=0.5,μ=0.66(dashed curve),μ=0.67(solid curve),andμ=0.70(dotted curve). Fig.9 (Color online)The ESPPs with ?(1)<0 forμ < μc,u0=0.01,δ=15,σ =0.25,κ1=20,κ2=3,α=0.5,μ=0.60(dashed curve),μ=0.61(solid curve),andμ=0.62(dotted curve). Fig.10 (Color online)The width of the ESPPs with ?(1)>0 for u0=0.01,δ =15,σ =0.25,κ1=20,κ2=3,α=0.5,μ=0.65(dashed curve),μ=0.75(solid curve),andμ=0.90(dotted curve). To derive the MK-dV equation we use the same stretched co-ordinates de fined by Eqs.(7)and(8),but the different types of expansion of the dependent variables: To further higher order of?,substituting Eqs.(7),(8),and(29)–(32)into Eqs.(2)–(4),and then taking the terms containing?2from Eq.(2)and thez-component of Eq.(3),and?3/2from Eq.(4),we obtain another set of equations: To solve this MK-dV,We consider a frameξ=η ?u0T(moving with speedu0).The stationary solitary wave solution of the MK-dV equation(Eq.(41))is given by (i)The MK-dV equation admits solitary wave solution with?(1)>0 only;(ii)The amplitude and width of the ESPPs increase with the increase in(κ2)as shown in Fig.11. Fig.11 (Color online)The ESPPs with ?(1)>0 for u0=0.01,σ =0.25,μ =0.7,κ1=20,δ=15,α =0.5,κ2=3.0(dashed curve),κ2=2.5(solid curve),and κ2=2.0(dotted curve). Fig.12 (Color online)The ESPPs with ?(1)>0 for u0=0.01,δ=15,μ =0.70,κ1=20,κ2=3,α =0.5,σ=0.50(dashed curve),σ=0.70(solid curve),and σ=0.90(dotted curve). Fig.13 (Color online)The ESPPs with ?(1)>0 for u0=0.01,δ=15,σ =0.25,κ1=20,κ2=3,α =0.5,μ=0.65(dashed curve),μ=0.75(solid curve),andμ=0.85(dotted curve). (iii)The amplitude and width of the ESPPs increase with the increase inσas shown in Fig.12. (iv)The amplitude and width of the ESPPs decrease with the increase inμas shown in Fig.13. To examine the effects of further higher order nonlinearity on the K-dV or MK-dV equations describing HIAWs in a magnetized plasma(containing containing dynamical heavy ions and bi-kappa distributed electrons of two distinct temperatures),one can derive a further higher order nonlinear equation.The latter(after performing few steps of mathematical calculations)can be directly given by[65?66] Fig.14 (Color online)The ESPPs(with ?(1)>0)for u0=0.01,σ =0.25,μ =0.7,κ2=3,δ=15,α =0.5,κ1=10(dashed curve),κ1=15(solid curve),and κ1=30(dotted curve). We have considered a magnetized plasma system consisting of inertial heavy ions and kappa distributed electrons of two distinct temperatures.We have derived the K-dV,MK-dV,and HMK-dV equations by using the reductive perturbation method to identify the basic features(polarity,amplitude,and width)of the ESPPs formed in such a magnetized plasma system.The results,which have been obtained from this theoretical investigation,can be pin-pointed as follows: (i)The K-dV and HMK-dV equations admit HIASW solutions with either?(1)>0(compressive)or?(1)<0(rarefactive).The polarity of the HIASWs depends on the critical valueμc(whereμc=0.64 forκ1=20,κ2=3,δ=15,σ=0.25,andα=0.5).On the other-hand,the MK-dV equation admits only HIASW solution with?(1)>0(compressive). (ii)The amplitude of the K-dV solitons become inif nitely large forA1?0,and thus the K-dV equation is no longer valid atA1?0,which has been avoided by deriving MK-dV and HMK-dV equations to study more highly nonlinear HIASWs. (iii)The amplitude and width of both positive and negative HIASWs(obtained from the numerical analysis of the solution of the K-dV equation)increase with the increase inκ1andκ2.However the amplitude of the positive HIASWs increases with the increase inδ.On the other-hand,the width decreases with the increase inα,and increases(decreases)with the increase inδfor its lower(upper)range. (iv)The amplitude of the K-dV HIASWs increases with the increase inT2andn01,but decreases with the rise ofT1andn02. (v)The width of K-dV HIASWs rises with the increase(decrease)inn01(n02). (vi)The amplitude and the width of the MK-dV HIASWs increase with the increase inκ2,T2andn01,but decrease with the increase inT1andn02. (vii)The amplitude and the width of the HMK-dV HIASWs slightly increase with the increase inκ1.This means that the effect of higher nonlinearity on K-dV and MK-dV HIASWs is insigni ficant. To conclude,the results of our present investigation are relevant to space(viz.Saturns magnetosphere,[43]pulsar magnetosphere,[67]upper part of the ionosphere,[68?70]lower part of the magnetosphere,[68?70]etc.).The dip shape solitary structures(known as cavitons[68?70])observed by Freja satellite[68,70]and Viking spacecraft[69?70]are similar to those predicted by our present theoretical investigation.We finally hope that our results should be useful in understanding the nonlinear eloctrostatic disturbances in the space plasma systems containing heavy ions and super-thermal electrons of two distinct temperatures. M.Sarker,B.Hosen,and M.R.Hossen are grateful to the Ministry of Science and Technology(Bangladesh)for awarding the National Science and Technology(NST)fellowship. [1]X.Gao,Q.Lu,X.Li,et al.,Phys.Plasmas 20(2013)072902. [2]X.Gao,Q.Lu,X.Tao,et al.,Phys.Plasmas 20(2013)092106. [3]X.Gao,Q.Lu,X.Li,et al.,Astrophys.J.780(2014)56. [4]Y.Ke,X.Gao,Q.Lu,and S.Wang,Phys.Plasmas 24(2017)012108. [5]F.F.Chen,Introduction to Plasma Physics and Controlled Fusion,2nd ed.,Plenum Press,New York(1984)p.297. [6]I.R.Durrani,G.Murtaza,and H.U.Rahman,Can.J.Phys.57(1979)642. [7]R.C.Davidson,Methods in Nonlinear Plasma Theory,Academic Press,New York(1972)p.15. [8]J.K.Chawla,M.K.Mishra,and R.S.Tiwary,Astrophys.Space Sci.347(2013)283. [9]A.A.Mamun,Phys.Rev.E 55(1997)1852. [10]M.R.Hossen,L.Nahar,S.Sultana,and A.A.Mamun,Astrophys.Space Sci.353(2014)123. [11]M.R.Hossen and A.A.Mamun,Braz.J.Phys.44(2014)673. [12]M.R.Hossen,L.Nahar,and A.A.Mamun,J.Korean Phys.Soc.65(2014)1863. [13]M.R.Hossen,L.Nahar,and A.A.Mamun,J.Astrophys.2014(2014)653065. [14]B.Hosen,M.G.Shah,M.R.Hossen,and A.A.Mamun,Euro.Phys.J.Plus 131(2016)81. [15]Q.M.Lu,B.Lembege,J.B.Tao,and S.Wang,J.Geophys.Res.113(2008)A11219. [16]M.Wu,Q.Lu,C.Huang,and S.Wang,J.Geophys.Res.115(2010)A10245. [17]R.Wang,Q.Lu,Y.V.Khotyaintsev,et al.,Geophys.Res.Lett.41(2014)4851. [18]C.Huang,Q.Lu,P.Wang,et al.,J.Geophys.Res.119(2014)6445. [19]E.Witt and W.Lotko,Phys.Fluids 26(1983)2176. [20]S.Qian,W.Lotko,and M.K.Hudson,Phys.Fluids 31(1988)2190. [21]V.A.Marchenko and M.K.Hudson,J.Geophys.Res.100(1995)19791. [22]K.E.Lonngren,Plasma Phys.25(1983)943. [23]Y.Nakamura,J.L.Ferreira,and G.O.Ludwig,J.Plasma Phys.33(1985)237. [24]Y.Nakamura,T.Ito,and K.Koga,J.Plasma Phys.49(1993)331. [25]M.J.Barlow,B.M.Swinyard,P.J.Owen,et al.,Science 342(2013)1343. [26]M.L.Burns,A.K.Harding,and R.Ramaty,Positronelectron Pairs in Astrophysics,American Institute of Physics,New York(1983). [27]F.C.Michel,Theory of Neutron Star Magnetosphere,Chicago University Press,Chicago(1991). [28]H.R.Miller and P.J.Witta,Active Galactic Nuclei,Springer,Berlin(1987). [29]P.Goldreich and W.H.Julian,Astrophys.J.157(1969)869. [30]M.J.Rees,inThe Very Early Universe,eds.by G.W.Gibbons,S.W.Hawking,and S.Siklas,Cambridge University Press,Cambridge(1983). [31]C.Vocks and G.Mann,Astrophys.J.593(2003)1134. [32]G.Gloeckler and L.A.Fisk,Astrophys.J.648(2006)L63. [33]Y.Yagi,V.Antoni,M.Bagatin,et al.,Plasma Phys.Cont.Fusion 39(1997)1915. [34]S.Preische,P.C.Efthimion,and S.M.Kaye,Phys.Plasmas 3(1996)4065. [35]C.C.Chaston,Y.D.Hu,and B.J.Fraser,Geophys.Res.Lett.24(1997)2913. [36]M.Maksimovic,V.Pierrard,and J.F.Lemaire,Astron.Astrophys.324(1997)725. [37]V.M.Vasyliunas,J.Geophys.Res.73(1968)2839. [38]D.Summers and R.M.Thorne,Phys.Fluids B 3(1991)1835. [39]M.A.Hellberg,R.L.Mace,T.K.Baluku,et al.,Plasmas 16(2009)094701. [40]T.Cattaert,M.A.Helberg,and R.L.Mace,Phys.Plasmas 14(2007)082111. [41]M.S.Alam,M.M.Masud,and A.A.Mamun,Plasma Phys.Rep.39(2013)1011. [42]B.Basu,Phys.Plasmas 15(2008)042108. [43]T.K.Baluku and M.A.Hellberg,Phys.Plasmas 19(2012)012106. [44]S.Hussain,Chin.Phys.Lett.29(2012)065202. [45]M.Shahmansouri,B.Shahmansouri,and D.Darabi,Indian J.Phys.87(2013)711. [46]S.Sultana and I.Kourakis,Plasma Phys.Control.Fusion 53(2011)045003. [47]P.Schippers,M.Blanc,N.Andre,et al.,J.Geophys.Res.113(2008)07208. [48]T.K.Baluku,M.A.Hellberg,and R.L.Mace,J.Geophys.Res.116(2011)04227. [49]H.R.Pakzad,Astrophys.Space Sci.331(2011)169. [50]I.Tasnim,M.M.Masud,M.Asaduzzaman,and A.A.Mamun,Chaos 23(2013)013147. [51]I.Tasnim,M.M.Masud,and A.A.Mamun,Astrophys.Space Sci.343(2013)647. [52]M.M.Masud,S.Sultana,and A.A.Mamun,Astrophys.Space.Sci.348(2013)99. [53]Q.Lu,S.Wang,and X.Dou,Phys.Plasmas 12(2005)072903. [54]W.F.El-Taibany,N.A.El-Bedwehy,and E.F.El-Shamy,Phys.Plasmas 18(2011)033703. [55]M.Shahmansouri,Astrophys.Space Sci.29(2012)105201. [56]S.A.Ema,M.R.Hossen,and A.A.Mamun,Phys.Plasmas 22(2015)092108. [57]S.A.Ema,M.R.Hossen,and A.A.Mamun,Contrib.Plasma Phys.55(2015)596. [58]M.R.Hossen,L.Nahar,S.Sultana,and A.A.Mamun,High Energy Density Phys.13(2014)13. [59]M.R.Hossen,L.Nahar,and A.A.Mamun,Phys.Scr.89(2014)105603. [60]M.R.Hossen and A.A.Mamun,Plasma Sci.Technol.17(2015)177. [61]M.G.Shah,M.M.Rahman,M.R.Hossen,and A.A.Mamun,Commun.Theor.Phys.64(2015)208. [62]M.G.Shah,M.M.Rahman,M.R.Hossen,and A.A.Mamun,Plasma Phys.Rep.42(2016)168. [63]P.K.Shukla and M.Y.Yu,J.Math.Phys.19(1978)2506. [64]A.A.Mamun,Astrophys.Space Sci.260(1998)507. [65]S.A.Elwakil,E.M.Abulwafa,E.K.El-Shewy,and H.M.Abd-El-Hamid,Adv.Space Res.48(2011)1578. [66]M.G.Shah,M.R.Hossen,and A.A.Mamun,J.Plasma Phys.81(2015)905810517. [67]S.K.Kundu,D.K.Ghosh,P.Chatterjee,and B.Das,Bulg.J.Phys.38(2011)409. [68]P.O.Dovner,A.I.Eriksson,R.Bostr¨om,and B.Holback,Geophys.Res.Lett.21(1994)1827. [69]R.Bostr¨om,G.Gustafsson,B.Holback,et al.,Phys.Rev.Lett.61(1988)82. [70]R.A.Cairns,A.A.Mamun,R.Bingham,et al.,Geophys.Res.Lett.22(1995)2709.
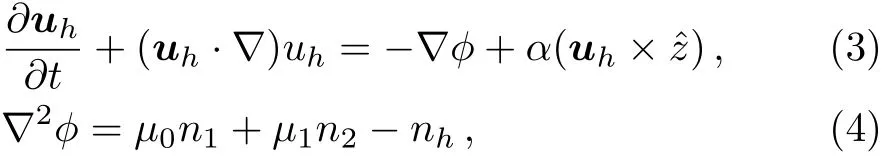
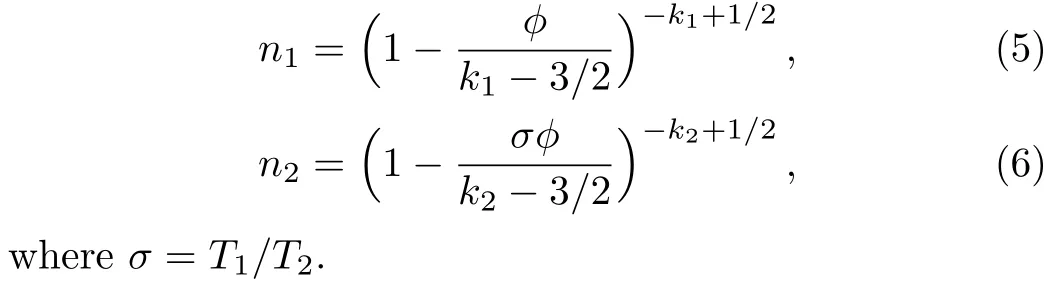
3 Nonlinear Equations
3.1 K-dV Equation
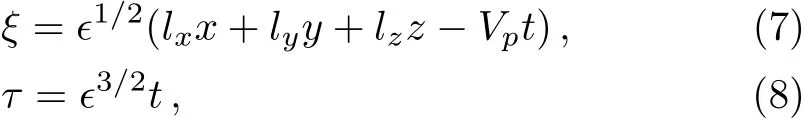
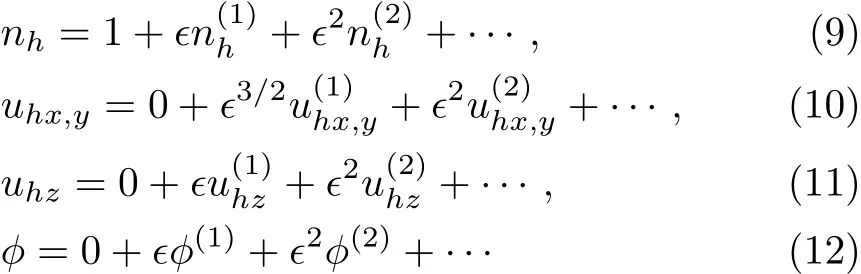
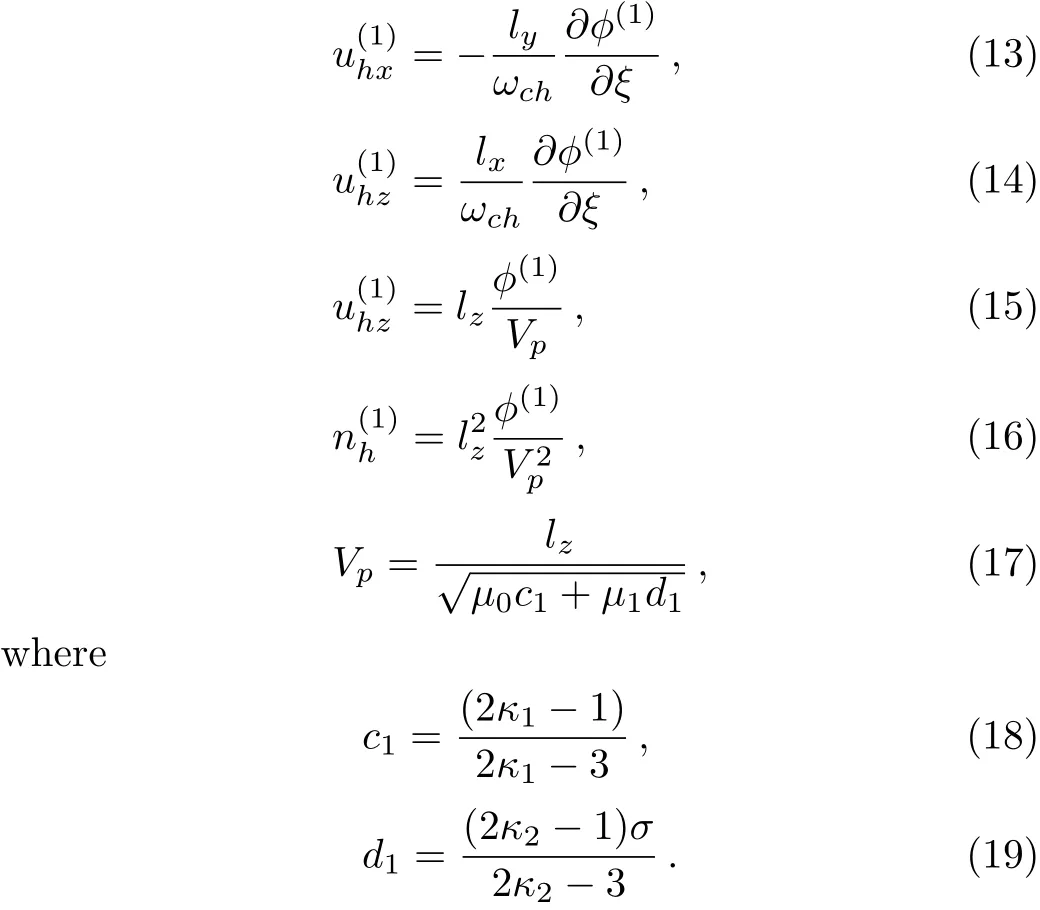


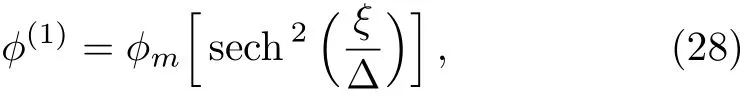


3.2 MK-dV Equation

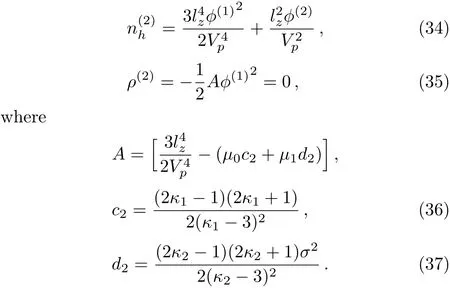


3.3 HMK-dV Equation

4 Discussion
 Communications in Theoretical Physics2018年1期
Communications in Theoretical Physics2018年1期
- Communications in Theoretical Physics的其它文章
- Ti Impurity Effect on the Optical Coefficients in 2D Cu2Si:A DFT Study?
- Simultaneous Effects of Impurity and Electric Field on Entropy Behavior in Double Cone-Like Quantum Dot
- Electron Acceleration by Beating of Two Intense Cross-Focused Hollow Gaussian Laser Beams in Plasma?
- Discrete Boltzmann Method with Maxwell-Type Boundary Condition for Slip Flow?
- Unique Outcomes of Internal Heat Generation and Thermal Deposition on Viscous Dissipative Transport of Viscoplastic Fluid over a Riga-Plate
- Spatial Dependent Spontaneous Emission of an Atom in a Semi-In finite Waveguide of Rectangular Cross Section?
