Noether Symmetry and Conserved Quantities of Fractional Birkhoffian System in Terms of Herglotz Variational Problem?
Xue Tian(田雪)and Yi Zhang(張毅)
1College of Mathematics and Physics,Suzhou University of Science and Technology,Suzhou 215009,China
2School of Science,Nanjing University of Science and Technology,Nanjing 210094,China
3College of Civil Engineering,Suzhou University of Science and Technology,Suzhou 215011,China
AbstractThe aim of this paper is to study the Herglotz variational principle of the fractional Birkhoffian system and its Noether symmetry and conserved quantities.First,the fractional Pfa ff-Herglotz action and the fractional Pfa ff-Herglotz principle are presented.Second,based on different definitions of fractional derivatives,four kinds of fractional Birkho ff’s equations in terms of the Herglotz variational principle are established.Further,the definition and criterion of Noether symmetry of the fractional Birkhoffian system in terms of the Herglotz variational problem are given.According to the relationship between the symmetry and the conserved quantities,the Noether’s theorems within four different fractional derivatives are derived,which can reduce to the Noether’s theorem of the Birkhoffian system in terms of the Herglotz variational principle under the classical conditions.As applications of the Noether’s t heorems of the fractional Birkhoffian system in terms of the Herglotz variational principle,an example is given at the end of this paper.
Key words:fractional Birkhoffian system,Herglotz variational problem,Noether symmetry,conserved quantity
1 Introduction
As is well known,the symmetry and the conserved quantity play important roles in the fields of mathematics,physics,dynamics,optimal control,and so on.The symmetry of a mechanical system is described by the invariance under an in finitesimal transformation,which has a profound in fluence on the dynamic behaviors and qualitative properties of a system.[1]The conserved quantity can reduce the dimensions and simplify the integral of the differential equation via reducing the degrees of freedom of a system.In 1918,Emmy Noether[2]noted the relationship between the symmetry and the conservation quantity and put forward Noether’s theorem.Since Noether’s theorem explains all the conservation laws of Newtonian mechanics,the studies of Noether’s symmetry and the conserved quantity have been one of the hot topics in the study of analytical mechanics and their applications in recent decades. So far,Noether symmetry and the conserved quantity have been studied in Lagrangian systems,[3?5]Hamiltonian systems,[6?8]Birkhoffian systems[9?11]as well as nonholonomic systems,[12?13]and so on.Not only that,but some scholars have studied Noether symmetry and conserved quantity in the model of fractional calculus.
The origin of the concept of fractional calculus was advanced in 1695 when L’Hopital and Leibniz discussed the significance of a function in the order of 1/2.However,the theories of fractional calculus were rarely studied because of the research difficulties and ambiguity of the research significance.Until in the end of the 1970s,Mandelbrot[14]discovered that a large number of fractional dimension examples exists in nature.Then,it is found that fractional calculus has a wide range of applications in quantum mechanics,chaotic dynamics,long-range dissipation,signal processing and so on.[15?19]In recent years,various models of fractional integral and derivative have been developed,such as Riemann-Liouville fractional derivatives,Caputo fractional derivatives,Riesz-Riemann-Liouville fractional derivatives,Riesz-Caputo fractional derivatives,and so on.In this paper,we will study these four kinds of fractional derivatives. In addition,fractional calculus has applied in a variety of mechanical systems.[20?29]Since Birkhoffian systems are natural generalizations of Lagrangian systems and Hamiltonian systems,it is significant to propose the theory of fractional Birkhoffian systems.Up to now,there are a series of results and applications of fractional Birkhoffian systems.[30?36]Besides,in 2014,Almeida and Malinowska[37]considered the fractional Herglotz variational principle,where fractionality stands in the dependence of the Lagrangian by Caputo fractional derivatives of Herglotz variables.
Herglotz variational principle,[38]proposed by Gustav Herglotz in 1930 firstly,gives a variational principle description of nonconservative systems even when the Lagrangian does not depend on time.The functional of Herglotz variational principle is defined by a differential equation,which generalizes the classical ones defining the functional by an integral.Before Georgieva and Guenther,[39]Noether’s theorems were applicable only to the classical variational principle and were not applied to the functional defined by different equations.Torres and his co-workers presented Noether’s theorem of higher-order variational problems of Herglotz type[40]and Noether’s first theorem based on Herglotz variational problems with time delay.[41]Besides,they also proposed Noether’s theorem for fractional Herglotz variational problems.[42?43]Zhang studied Noether’s theorem based on Herglotz variational problems in phase space and of Birkhoffian system.[44?46]However,applications of fractional Birkhoffian systems for the Herglotz variational principle have been not investigated in previous works.
In this paper,we will study Noether symmetry and conserved quantities of the fractional Birkhoffian system in terms of the Herglotz variational problem.First of all,a brief summery of fractional derivatives and their properties are presented in Sec.2.In Sec.3,we present the fractional Pfa ff-Herglotz action and the fractional Pfa ff-Herglotz principle.In Sec.4,according to the fractional Pfa ff-Herglotz principle,we establish four kinds of fractional Birkho ff’s equations based on different definitions of fractional derivatives in terms of the Herglotz variational problem.In Sec.5,we give the definition and criterion of Noether symmetry of the fractional Birkhoffian system in terms of the Herglotz variational problem,and we derive the Noether’s theorems of the fractional Birkhoffian system in terms of the Herglotz variational problem.In Sec.6,in order to illustrate the method and results,we give an example and find four kinds of conserved quantities based on different definitions of fractional derivatives.Finally,we give the conclusions in Sec.7.
2 Fractional Derivatives and Properties
For the convenience of readers,we introduce the representations of Riemann-Liouville derivatives,Caputo derivatives,Riesz-Riemann-Liouville derivatives and Riesz-Caputo derivatives.Assume that the function f(ξ)is continuous and integrable in every finite interval(a,t)and(t,b). The left and the right Riemann-Liouville derivatives are[47]

The left and the right Caputo derivatives are[47]
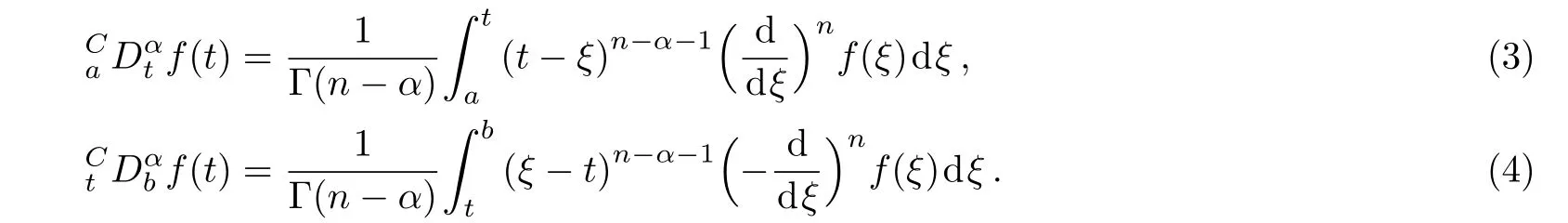
The Riesz-Riemann-Liouville and Riesz-Caputo derivatives are[47]

Here,D is the traditional derivative operator,α is the order of fractional derivatives such that n?1≤α Here γ ∈ t[0,1],γ means the dispensed quantities of the left and the right fractional derivatives,which can be distributed as needed. In this paper,we will need formulae for fractional integration by parts as follows given in Ref.[49]: According to the ideas of the generalized variational principle proposed by Herglotz,[38]the Herglotz variational problem of the fractional Birkhoffian system can be formulated as follows. Determine the trajectories aν(t)satisfying the boundary conditions for fixed real numbers a,b,and the function z satis fies the differential equation subject to the initial condition then z(b)is the extreme(minimize or maximize value),i.e. where B(t,aμ(t),z(t))is the Birkhoffian,Rν(t,aμ(t),z(t))areBirkho ff’sfunctions,aν(t)(ν=1,2,...,2n)are Birkho ff ’s variables,is a unified symbol ofandand zaare constants.We refer to the above variational problem as the Herglotz variational problem of the fractional Birkhoffian system.Then,functional z is the fractional Pfa ff-Herglotz action if z satis fies Eq.(16). Taking the calculation of the variation to Eq.(16),we have Considering the commutative relation δ˙z=(d/dt)δz,the formula(19)can be written as follows where And Eq.(20)satis fies the initial condition The solution of the above initial value problem is When t=b,the functional z(t)yields its extremum,and we obtain δz(b)=0.Let From the formula(22)and Eq.(23),we have Equation(24)is called fractional Pfa ff-Herglotz principle. Remark 1 When α,β → 1,the fractional Pfa ff-Herglotz principle(24)can be reduced to the integer Pfa ff-Herglotz principle[49] Using the above Pfa ff-Herglotz principle,we can deduce to fractional Birkho ff’s equations in terms of the Herglotz variational problem based on different definitions of fractional derivatives. Let when 0< α,β <1,using Eqs.(9)and(10),we have Using Eqs.(26)and(27),Eq.(24)can be expressed as According to the fundamental lemma of the calculus of variations,we obtain De finition 1 Equations(29)are called fractional Birkho ff’s equations in terms of the Herglotz variational problem based on combined Riemann-Liouville derivatives. When γ =1,Eqs.(29)are reduced to left fractional Birkho ff ’s equations in terms of the Herglotz variational problem based on Riemann-Liouville derivatives where When γ =0,Eqs.(29)are reduced to right fractional Birkho ff ’s equations in terms of the Herglotz variational problem based on Riemann-Liouville derivatives where De finition 2 Let when 0<α<1,we have Then,Eqs.(32)are called fractional Birkho ff’s equations in terms of the Herglotz variational problem based on Riesz-Riemann-Liouville derivatives. De finition 3 Let when 0<α,β<1,we have Then,Eqs.(33)are called fractional Birkho ff’s equations in terms of the Herglotz variational problem based on combined Caputo derivatives. When γ =1,Eqs.(33)are reduced to left fractional Birkhof’s equations in terms of the Herglotz variational problem based on Caputo derivatives where When γ =0,Eqs.(33)are reduced to right fractional Birkho ff ’s equations in terms of the Herglotz variational problem based on Caputo derivatives where De finition 4 Let when 0<α<1,we have Then,Eqs.(36)are called fractional Birkho ff’s equations in terms of the Herglotz variational problem based on Riesz-Caputo derivatives. Remark 2 In fact,selecting γ =1/2 and β = α,Eq.(32)can also be obtained by Eq.(29),and Eqs.(36)can also be obtained by Eqs.(33).When α,β → 1,fractional Birkho ff’s equations in terms of the Herglotz variational problem(29)–(36)can be reduced to the classical Birkho ff’s equations in terms of the Herglotz variational problem[45] Introducing the in finitesimal transformations of r-parameter finite transformation group Grwith respect to time t and Birkho ff ’s variables aν,they are and their expansion formulae are where εσ(σ=1,2,...,r)are the in finitesimal parameters,τσandare the generators of the in finitesimal transformations.Under the action of the transformations(37),the corresponding Pfa ff-Herglotz action z will be transformed to the following form For any function F(t),we haveAnd noting the commutative relationwe can get easily Calculating the total variation for the differential equation(16),we have Using the formula(39)and considering Eq.(16),from Eq.(40)we have The solution?z(t)of Eq.(41)is given by Obviously?z(a)=0,the formula(42)can be changed to Since and considering the formulae(42)and(43)can be expressed as where According to the concepts of Noether symmetry,[2]we can establish the definition and criterion of Noether symmetric transformations of the fractional Birkhoffian system in terms of the Herglotz variational problem as follows. De finition 5 If the fractional Pfa ff-Herglotz action is invariant for t=b under the in finitesimal transformations(37)of group,i.e.for each of the in finitesimal transformation,the formula holds,then the in finitesimal transformations are called the Noether symmetric transformations of the fractional Birkhoffian system in terms of the Herglotz variational problem. By use of the definition,fractional Birkho ff’s equations in terms of the Herglotz variational problem and formulae(46),we obtain the following criterion. Criterion 1 For the fractional Birkhoffian system in terms of the Herglotz variational problem,if the in finitesimal transformations(38)satisfy the following condition then the transformations(38)are the Noether symmetric transformations of the fractional Birkhoffian system in terms of the Herglotz variational problem.Now,let us derive the Noether’s theorems of the fractional Birkhoffian systems based on the different definitions of fractional derivatives in terms of the Herglotz variational problem. Theorem 1 For the fractional Birkhoffian system in terms of the Herglotz variational problem based on combined Riemann-Liouville derivatives,if the in finitesimal transformations(38)of group are the Noether symmetric transformations,the system exists with r-linear independent conserved quantities,which are Proof Because the in finitesimal transformations(38)are the Noether symmetric transformations of the system,according to the definition,we have Substituting the formulae(7)and(47)into the above formula,we obtain Substituting the fractional Birkho ff’s equations in terms of the Herglotz variational problem(29)into the above expression,considering the independence of εσand the arbitrariness of the integral interval[a,b],we get Integrating it,we can obtain the conserved quantities(51),and thus,the theorem is proved. Theorem 1 is called Noether’s theorem of the fractional Birkhoffian system based on combined Riemann-Liouville derivatives in terms of the Herglotz variational problem.Similarly,we can get the following theorems. Theorem 2 For the fractional Birkhoffian system in terms of the Herglotz variational problem based on Riesz-Riemann-Liouville derivatives,if the in finitesimal transformations(38)of group are the Noether symmetric transformations,the system exists with r-linear independent conserved quantities,which are Theorem 3 For the fractional Birkhoffian system in terms of the Herglotz variational problem based on combined Caputo derivatives,if the in finitesimal transformations(38)of group are the Noether symmetric transformations,the system exists with r-linear independent conserved quantities,which are Theorem 4 For the fractional Birkhoffian system in terms of the Herglotz variational problem based on Riesz-Caputo derivatives,if the in finitesimal transformations(38)of group are the Noether symmetric transformations,the system exists with r-linear independent conserved quantities,which are Theorems 2,3,4 are called Noether’s theorem of the fractional Birkhoffian system in terms of the Herglotz variational problem based on Riesz-Riemann-Liouville derivatives,combined Caputo derivatives and Riesz-Caputo derivatives. When α,β → 1,Theorems 1–4 can be reduced to the classical Noether’s theorem of Birkhoffian system in terms of the Herglotz variational problem: Remark 3 For the Birkhoffian system in terms of the Herglotz variational problem,if the in finitesimal transformations(38)of group are the Noether symmetric transformations,then the system exists with r-linear independent conserved quantities,which are Remark 3 is the classical Noether’s theorem of the Birkhoffian system in terms of the Herglotz variational problem.[45] Try to find the conserved quantities of the following fractional Birkhoffian system in terms of the Herglotz variational problem where the functional z is defined by the differential equation First,substituting Eqs.(56)into thefractional Birkho ff’s equations in terms of the Herglotz variational problem based on combined Riemann-Liouville derivatives(29),we can obtain According to the criterion,the formula(50)can be changed to Equation(59)has a solution By Theorem 1,we obtain When γ =1/2 and β = α,Eqs.(58)and(59)are reduced to the fractional Birkho ff’s equations and criterion in terms of the Herglotz variational problem based on Riesz-Riemann-Liouville derivatives.Then,we can find the solution(60)is also one of the transformations.By Theorem 2,we obtain Next,substituting Eqs.(56)into thefractional Birkho ff’s equations in terms of the Herglotz variational problem based on combined Caputo derivatives(33),we can obtain At the moment,the formula(50)can be changed to Equation(64)has a solution By Theorem 3,we obtain Similarly,when γ =1/2 and β = α,we can obtain the Noether’s theorem of the fractional Birkhoffian system in terms of the Herglotz variational problem based on Riesz-Caputo derivatives In this paper,we define the fractional Pfa ff-Herglotz action and present the fractional Pfa ff-Herglotz principle firstly.And then,fractional Birkho ff’s equations,criterion of Noether symmetry and Noether’s theorems of the fractional Birkhoffian system in terms of the Herglotz variational problem based on four different definitions of fractional derivatives are obtained.The theorems not only can reduce to the Noether’s theorem of the Birkhoffian system for the Herglotz variational problem under classical conditions,but also can become the Noether’s theorem of the Birkhoffian system when the functional z is independent of time.The traditional Lagrangian,Hamiltonian and Birkhoffian systems,the fractional Lagrangian,Hamiltonian and Birkhoffian systems,as well as the traditional Lagrangian,Hamiltonian and Birkhoffian systems for the Herglotz variational problem are special cases of the fractional Birkhoffian system for the Herglotz variational problem.Obviously,the method and results in this letter are of more universal significance. Besides,fractional Herglotz variational principle provides an effective method to deal with fractional conservative and nonconservative systems systematically.Therefore,fractional mechanical systems in terms of the Herglotz variational problem may be taken a deeper study in future.
3 Herglotz Variational Principle of Fractional Birkhoffian System







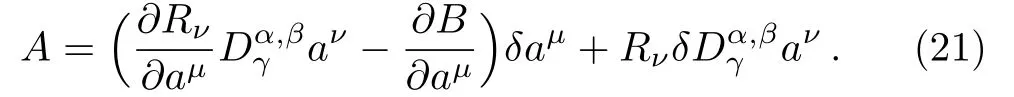



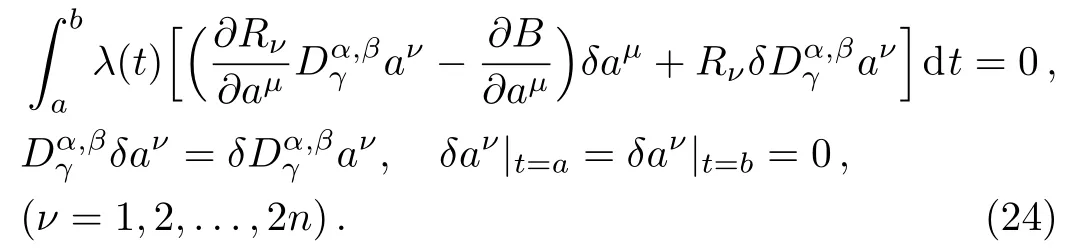

4 Fractional Birkho ff’s Equations in Terms of Herglotz Variational Problem
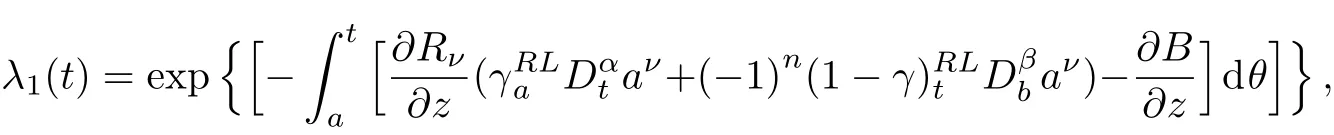
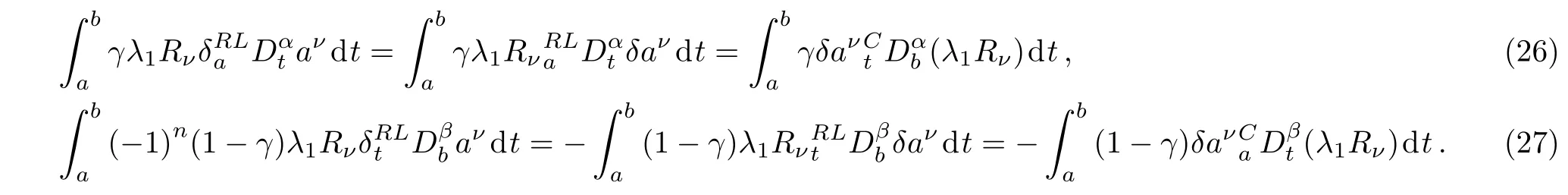
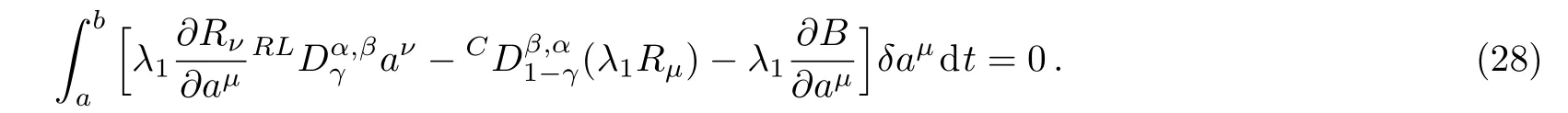
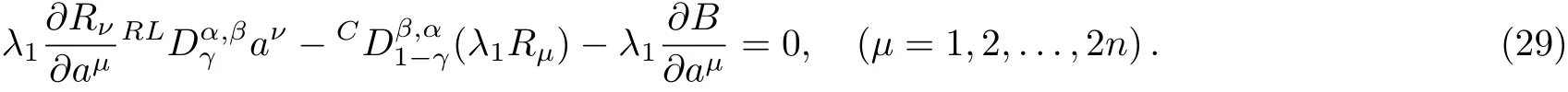
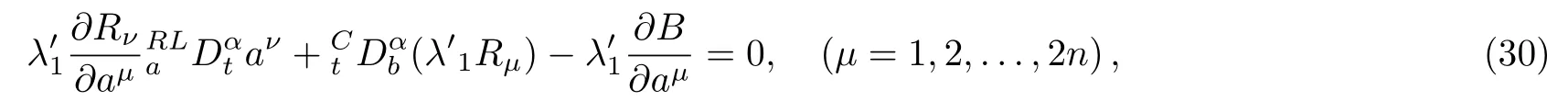
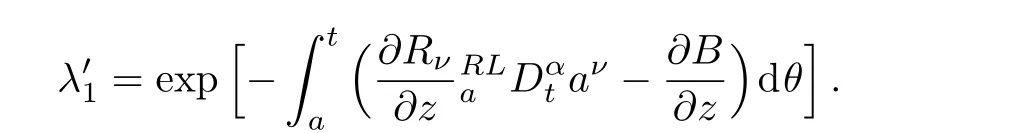

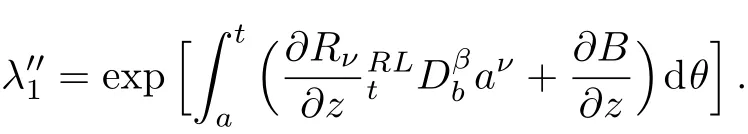



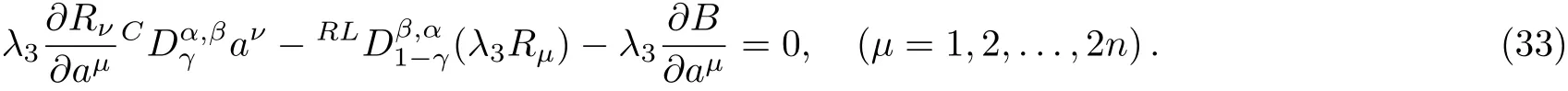
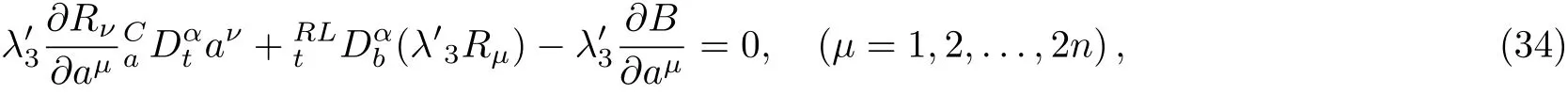
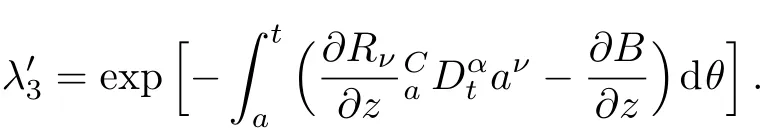

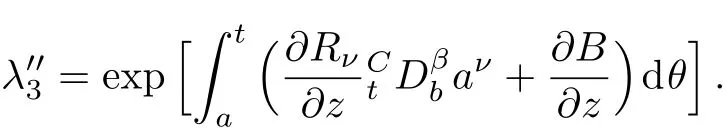

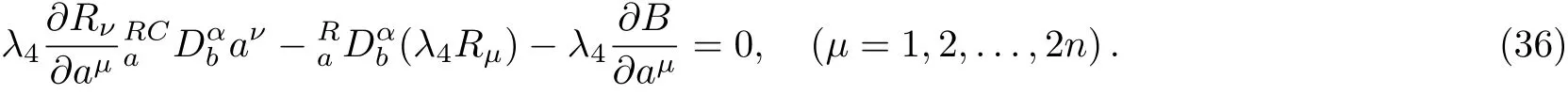

5 Noether Symmetry and Conserved Quantities of Fractional Birkhoffian System in Terms of Herglotz Variational Problem





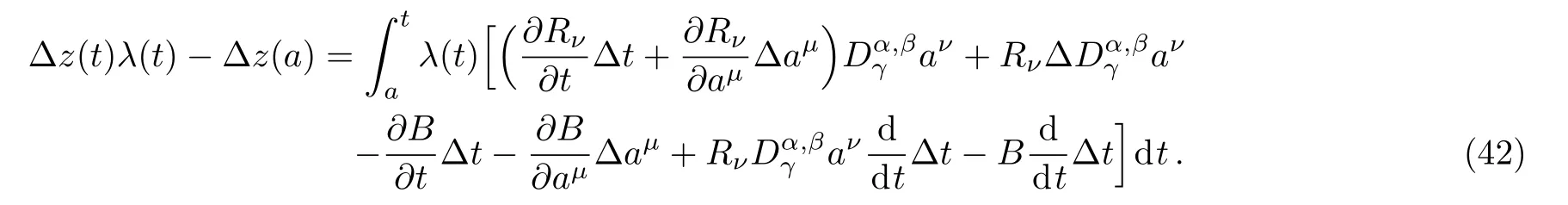

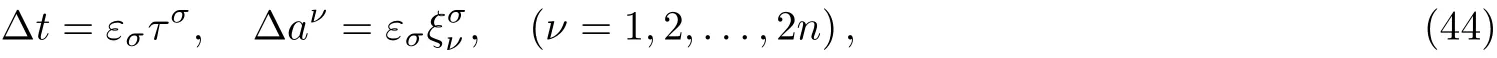
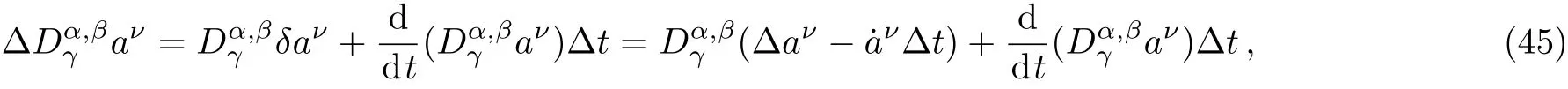
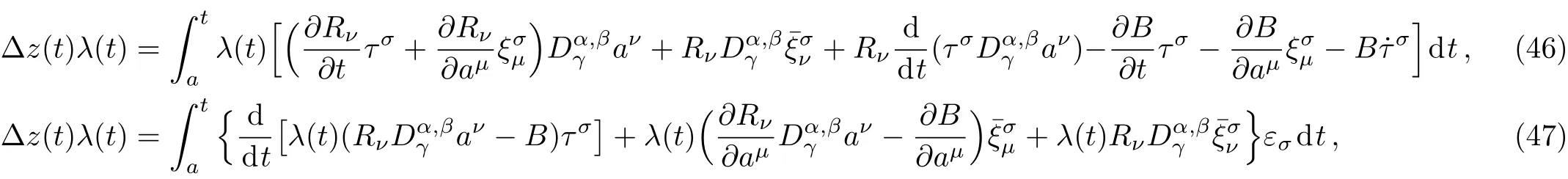


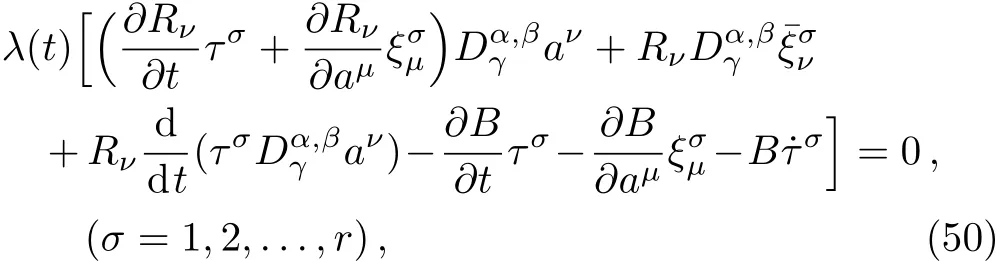





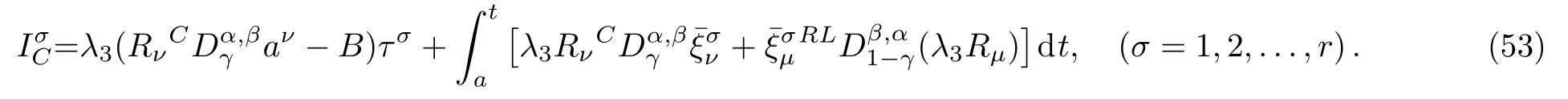
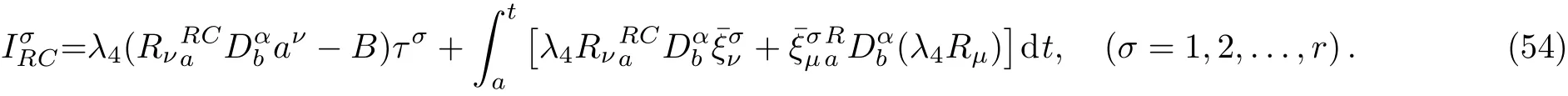
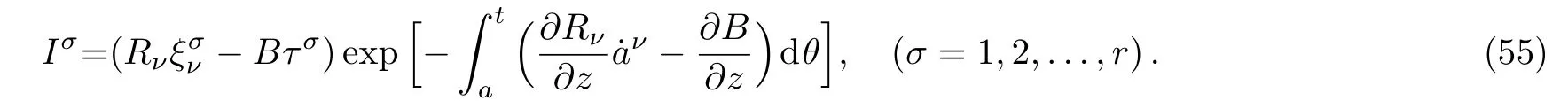
6 Example
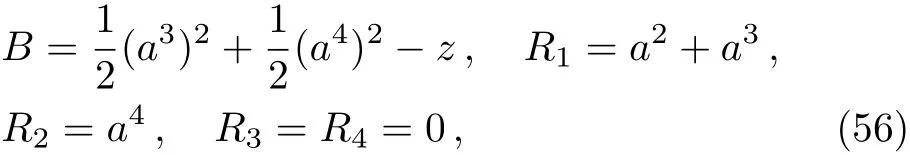
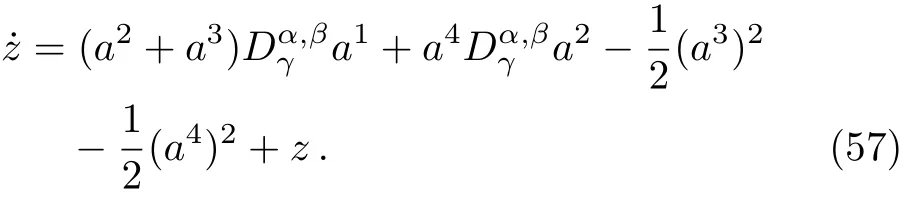
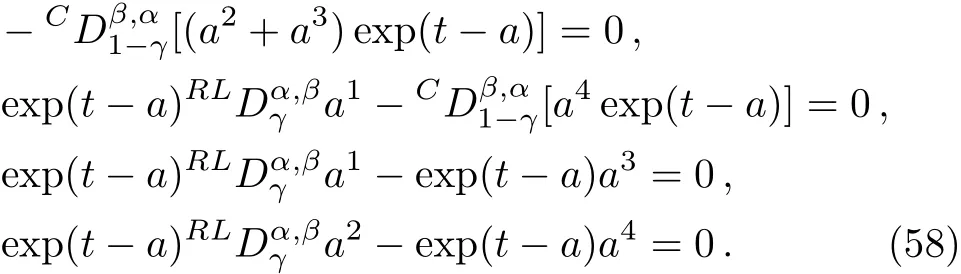

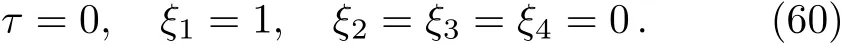
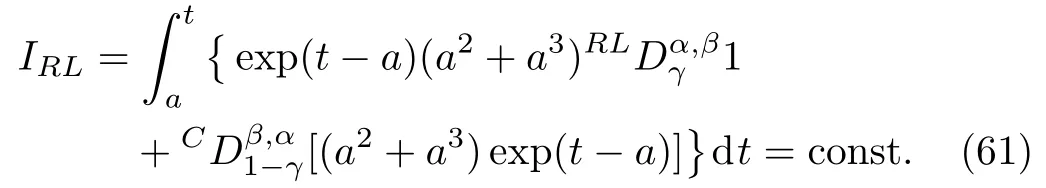
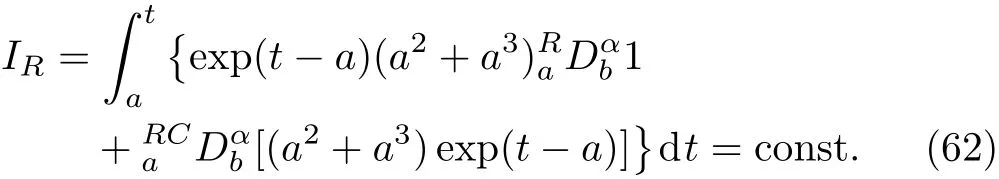


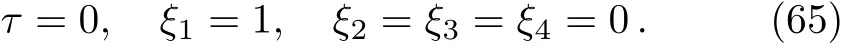
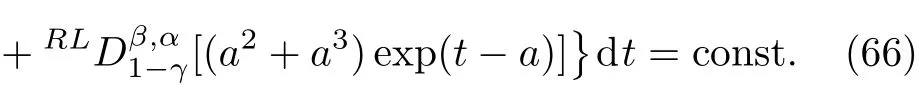
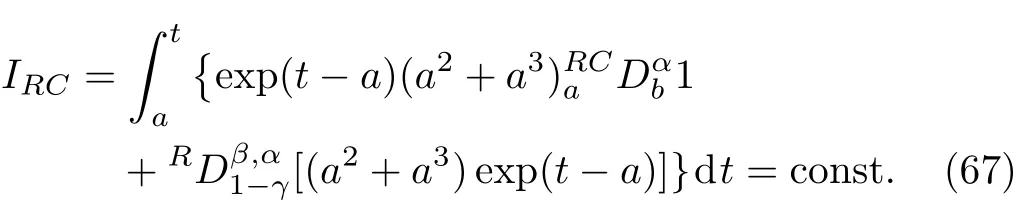
7 Conclusion
 Communications in Theoretical Physics2018年9期
Communications in Theoretical Physics2018年9期
- Communications in Theoretical Physics的其它文章
- Vertical Sediment Concentration Distribution in High-Concentrated Flows:An Analytical Solution Using Homotopy Analysis Method
- Significance of Darcy-Forchheimer Porous Medium in Nano fluid Through Carbon Nanotubes
- Third-Order Optical Nonlinearity in Two-Dimensional Transition Metal Dichalcogenides?
- Nano Fluid Flow Analysis in the Presence of Slip Effects and Wall Properties by Means of Contraction and Expansion?
- Improving the Performance of Practical Decoy-State Measurement-Device-Independent Quantum Key Distribution with Biased Basis Choice?
- Cylindrical Three-Dimensional Dust-Ion Acoustic Propagation in Plasmas
