置換群S6上的一類Hopf代數(shù)結(jié)構(gòu)
吳美云,唐秋林,羅秀花,姜會玲
(南通大學(xué)理學(xué)院,江蘇南通 226007)
1 引言
通常來講,要構(gòu)造一個Hopf代數(shù)是件很不容易的事.然而,近年來,很多數(shù)學(xué)家開始利用箭向來研究代數(shù)結(jié)構(gòu)[1?3],得到很多可交換與不可交換的Hopf代數(shù)[4?5].我們在文獻(xiàn)[6–7]中也借助于箭向構(gòu)造了群上的大量的Hopf代數(shù).
設(shè)G是群,kG是代數(shù)閉域k上的一個群代數(shù),則Hopf雙模范疇等價于直積范疇C∈K(G)MkZu(C),這里K(G)是群G 的全體共軛類,映射
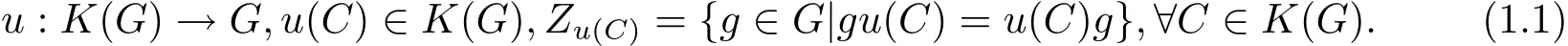
MkZu(C)表示右kZu(C)模[5,8].2002年,由于數(shù)學(xué)家Cibils和Rosso引入了Hopf箭向和群的分歧[8],使得利用箭向構(gòu)造Hopf代數(shù)成為可能[5].2008年,張壽全教授等給出了Sn(此時n≠6[9])是完全群時的分歧系統(tǒng),由此可以構(gòu)造出一批Hopf代數(shù)[10].那么對于非完全群S6,如何構(gòu)造其上的Hopf代數(shù)呢?本文想在這方面做些探討.
2011年,Andruskiewitsch,Fantino,Grana以及Vendramin研究出對稱群上的有限維逐點Hopf代數(shù)都是平凡的,且對于對稱群S6,其上的一型路Hopf代數(shù)都是無限維的[11].所以我們要構(gòu)造的一型路Hopf代數(shù)都是無限維的.
本文約定在代數(shù)閉域k上討論,并且k的特征char(k)≠2.所有代數(shù),余代數(shù),Hopf代數(shù)等都在域k上討論.與Hopf代數(shù)有關(guān)的概念參見文獻(xiàn)[12].
2 非完全群S6的特征標(biāo)和自同構(gòu)之間的關(guān)系
由于非完全群S6也是置換群,故S6中任意兩個元素有相同的共軛類當(dāng)且僅當(dāng)它們有相同的循環(huán)結(jié)構(gòu).從而有以下引理.
引理2.1[13]設(shè)S6是包含6個元素的集合的全體置換做成的群,Aut(S6)是S6的自同構(gòu)群,則Aut(S6)=Inn(S6)<δ>,其中δ為2階外自同構(gòu).因此Aut(S6)是一個1440階的群,是S6的內(nèi)自同構(gòu)群和一個2階群的半直積.
由于群S6可由?={(12),(13),(14),(15),(16)}生成,令φ:S6→S6是一個映射,定義
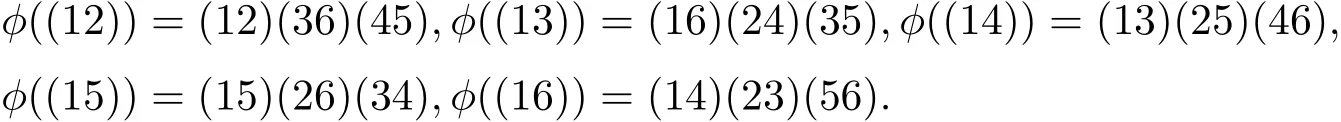
可以驗證φ定義了S6的一個外自同構(gòu).
令σ=(12345),iσ是由σ誘導(dǎo)的S6的內(nèi)自同構(gòu),即任意g∈S6,定義iσ:S6→S6,iσ(g)= σgσ?1.令 δ=iσφ,則 δ是2階外自同構(gòu).由此得以下結(jié)論.
定理2.2任意h∈S6,定義
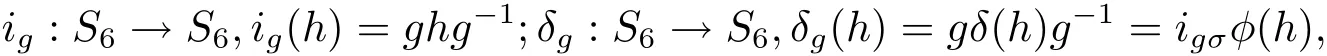
則Aut(S6)={ig|g∈S6}∪{δg|g∈S6}.
注 (i)由于?={(12),(13),(14),(15),(16)}可以生成置換群S6,所以ig,δg只需要定義在?上即可.
(ii)經(jīng)過計算,可得
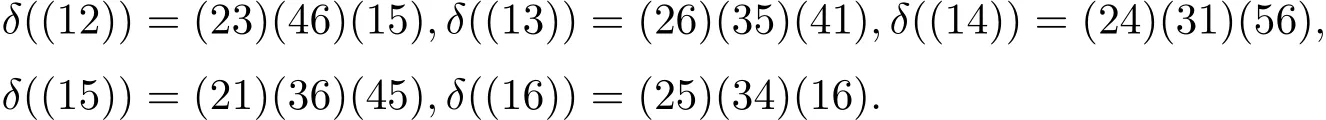
用C1,C2,C3,C4,C5,C6,C7,C8,C9,C10,C11表示S6的全體共軛類,分別用(1),(12),(123),(1234),(12345),(123456),(12)(34),(12)(345),(12)(3456),(12)(34)(56),(123)(456)作為這些共軛類的代表元.考慮S6的共軛類與特征標(biāo)的關(guān)系,得到如表1[13?14].
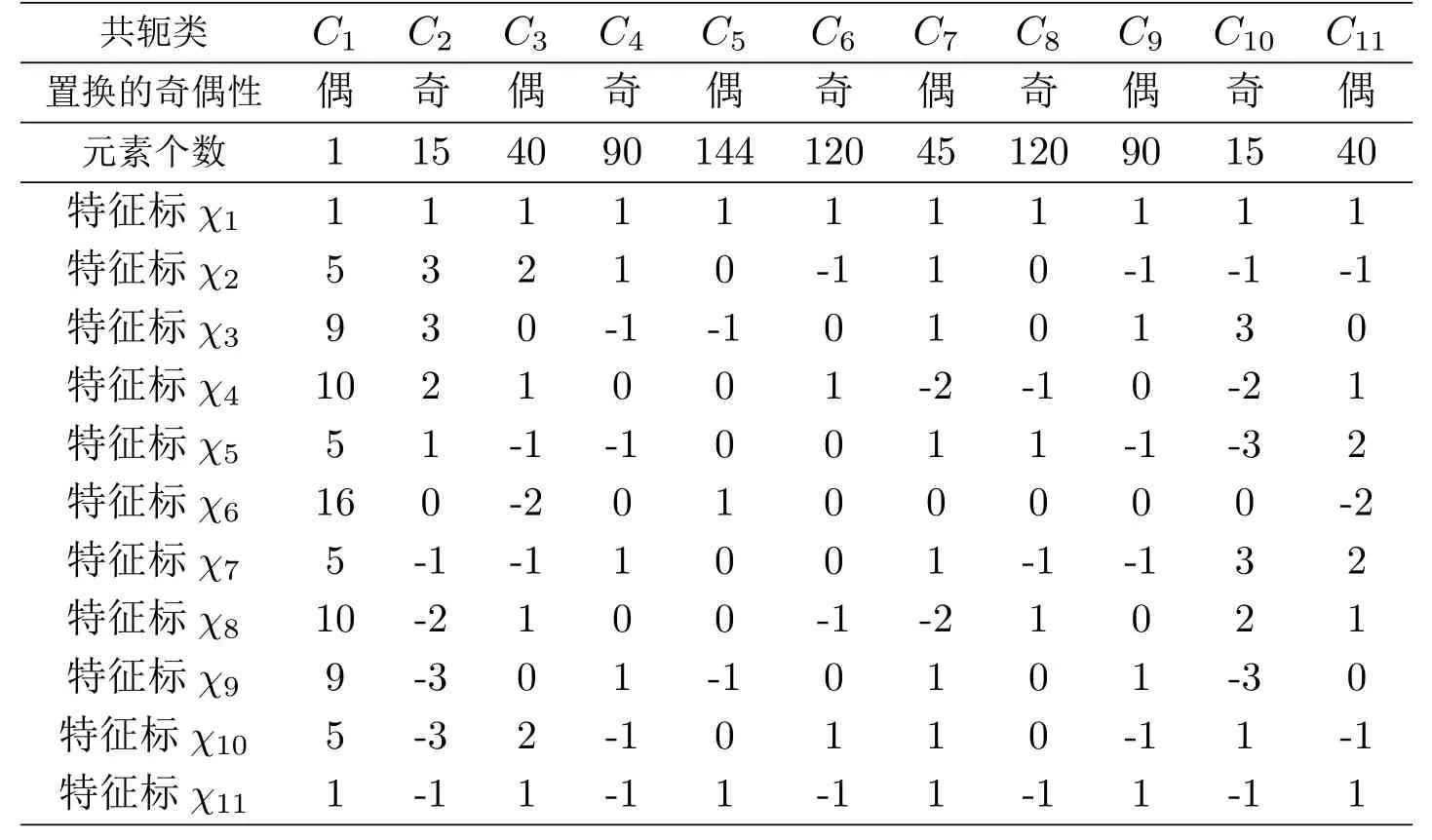
表1
定理2.3 設(shè)S6是6個元素上的置換群,ig,δg如定理2.2中所述,記={χ1,χ2,···,χ11},其中χ1,χ2,···,χ11如表1中所述.則對于任意g∈ S6,有
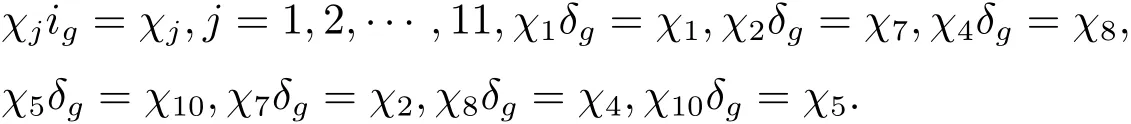
證 容易看出,對于任意g∈S6,有 χjig=χj,j=1,2,···,11,χ1δg= χ1.下面證明后面6個關(guān)系式.
記?={(12),(13),(14),(15),(16)}.任意h∈?,由于自同構(gòu)保持元素的階和共軛類的階,因此通過簡單計算,有 χ4δg(h)= χ4(gδ(h)g?1)= χ4δ(h)= ?2, χ8(h)= ?2. 所以χ4δg= χ8. 類似的,得到 χ8δg= χ4;χ2δg= χ7; χ7δg= χ2;χ5δg= χ10; χ10δg= χ5.
由此,不失一般性,可設(shè)

這里a是一個正整數(shù),b1,b2,···,b10是非負(fù)整數(shù).
3 S6上的分次Hopf代數(shù)結(jié)構(gòu)
設(shè)N表示自然數(shù)集合,得到如下結(jié)論.
定理3.1設(shè)G=S6是置換群,m是自然數(shù),N表示自然數(shù)集合,r是G的關(guān)于rCi,i=1,2,···,11的分歧,Q=(G,r)是對應(yīng)的Hopf箭向.如果rC1=m > 0,rCi=0,i=2,3,···,11,那么路余代數(shù)kQc有不同構(gòu)的分次Hopf代數(shù)結(jié)構(gòu)kQc(αχs),s∈N10,其個數(shù)與不等式s1+2s2+s3+2s4+2s5+s6+s9≤m的非負(fù)整數(shù)解的個數(shù)相同.記1,2,···,m.則在 (kQ1,αχs) 上的 kG-模作用為


任意t=2,3,4,5,6,

任意t=3,4,5,6,

任意t=2,4,5,6,
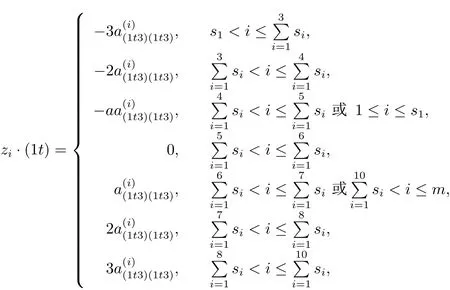
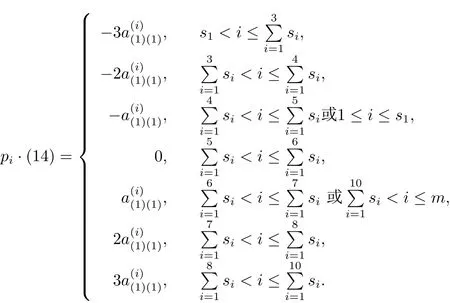
任意t=2,3,5,6,

任意t=2,3,4,6,

任意t=2,3,4,5,

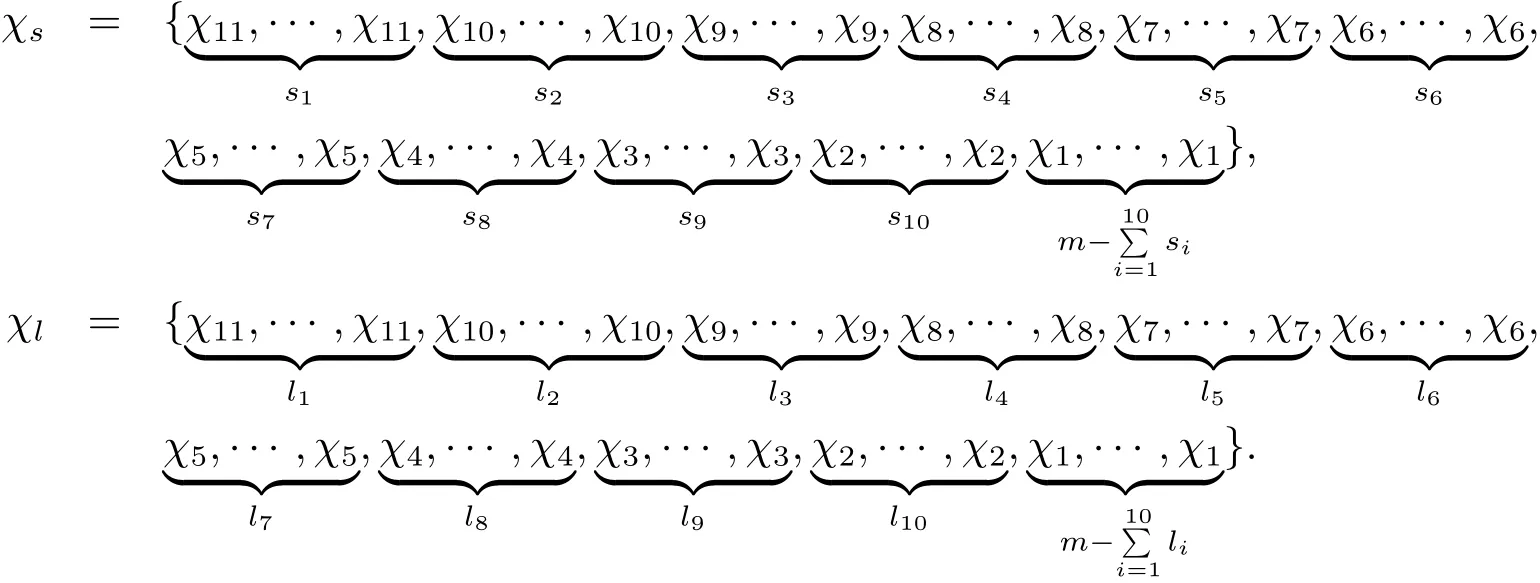
證 設(shè)r是群G的滿足rC1=m>0,rCi=0,i=2,3,···,11的分歧,Q=(G,r)是對應(yīng)的Hopf箭向.則由文獻(xiàn)[5]得對任意x,y∈G,x≠y,有y(Q1)x是空集. 顯然任意 s=(s1,s2,···,s10)∈ N10,設(shè). 由于 rC1=m > 0,rCi=0,i=2,3,···,11, 所以1≤i≤m}是關(guān)于r的帶有特征標(biāo)的全部分歧系統(tǒng),簡記為RSC.對于任意s,l∈N10,有χs≌ χl當(dāng)且僅當(dāng) s=l或 s1=l2,s2=l7,s3=l3,s4=l8,s5=l10,s6=l6,s7=l2,s8=l4,s9=l9,s10=l5.
事實上,如果s=l,顯然χs=χl,自然有χs≌χl.對于其他情形,由于
由定理 2.3, 任意 g ∈ G,χ1δg= χ1,χ2δg= χ7,χ4δg= χ8,χ5δg= χ10,χ7δg= χ2,χ8δg= χ4,χ10δg= χ5,有
(i)δg:G→G是一個群同構(gòu).
(ii) 任意 α,β ∈ G,顯然 δ(αβ)= δ(α)δ(β).固定映射u:K(G)→G,
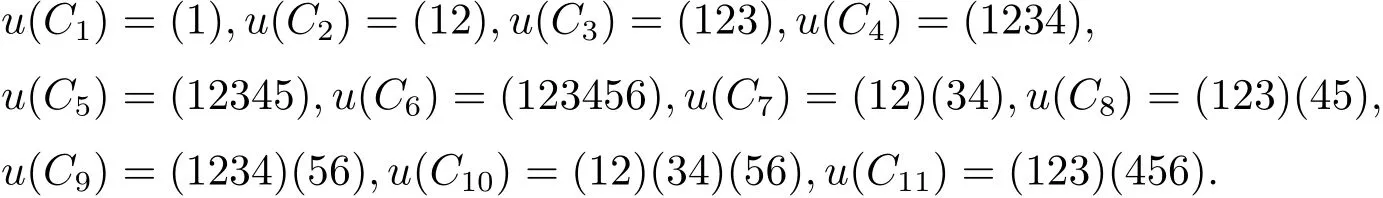
任意Ci∈K(G),g∈G,存在元素hCi∈G使得
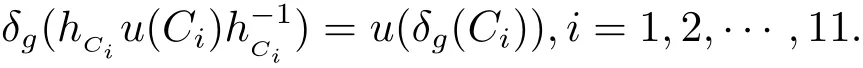
事實上,有
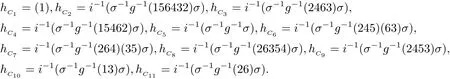
(iii)任意C ∈K(G),存在雙射fC1:IC1(r)→Iδg(C1)(r)使得
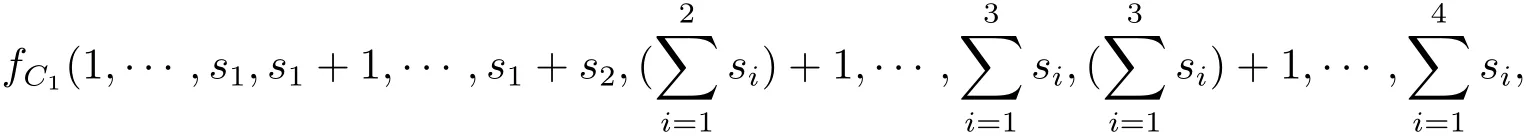
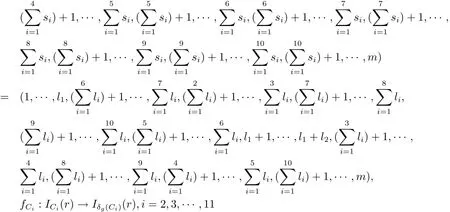
是空映射.由定理2.3,對任意h∈Zu(C1),
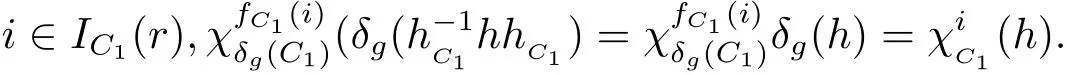
故 χs≌ χl.
由此,{χs|s∈N10}是關(guān)于r的互不同構(gòu)的所有的RSC,該集合的基數(shù)恰好等于不等式s1+2s2+s3+2s4+2s5+s6+s9≤m的非負(fù)整數(shù)解的個數(shù).由于域k的特征char(k)≠2,所有右kG-模是逐點的.由文獻(xiàn)[5]的定理2.2,得到路余代數(shù)kQc的不同構(gòu)的余路Hopf代數(shù)結(jié)構(gòu)kQc(αχs),s∈N10.設(shè)s∈N10.為簡便起見,記
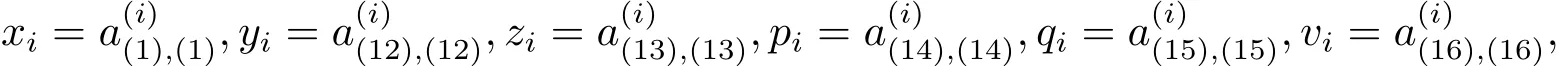
i=1,2,···,m.由文獻(xiàn)[5]的等式(2.2),得到(kQ1,αχs)上的所有kG-模作用.證畢.
推論 3.2 設(shè) kQc(αχs),s∈ N10如定理 3.1中所述,則 kQc(αχs)的子 Hopf代數(shù)kG[kQ1;αχs]由 (12),(13),(14),(15),(16),xi,yi,zi,pi,qi,vi,i=1,2,···,m 生成,生成關(guān)系為
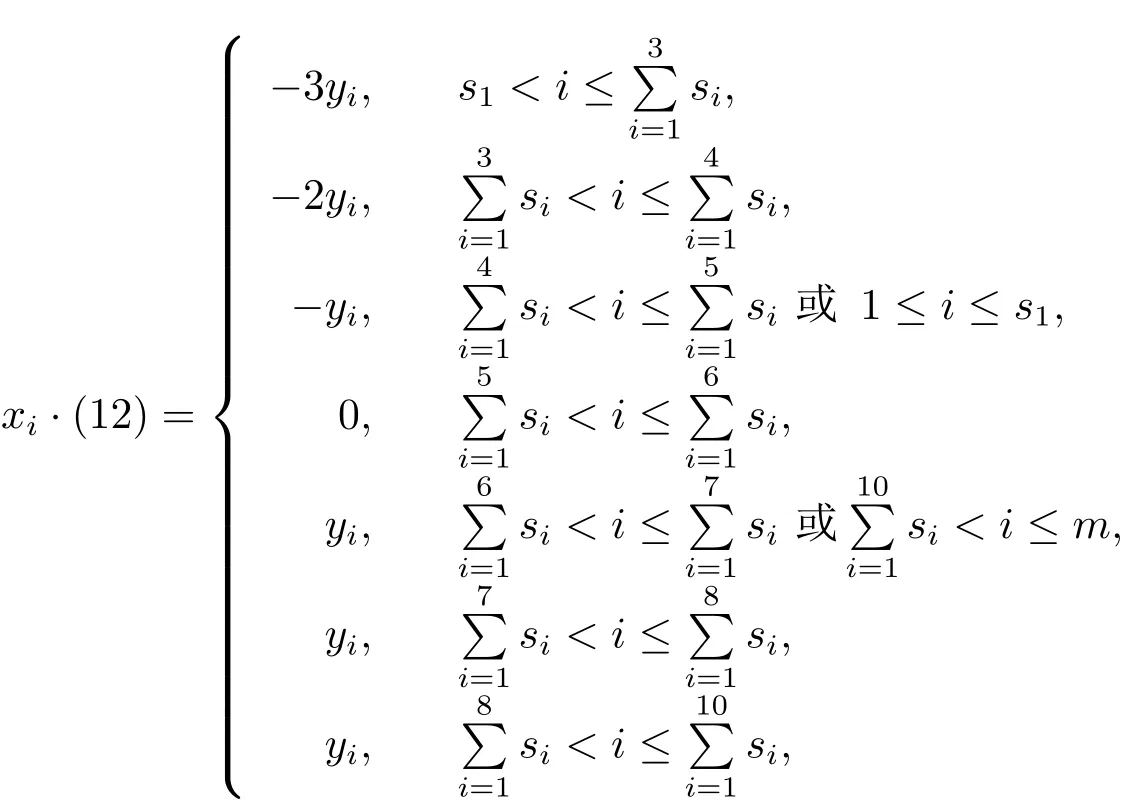

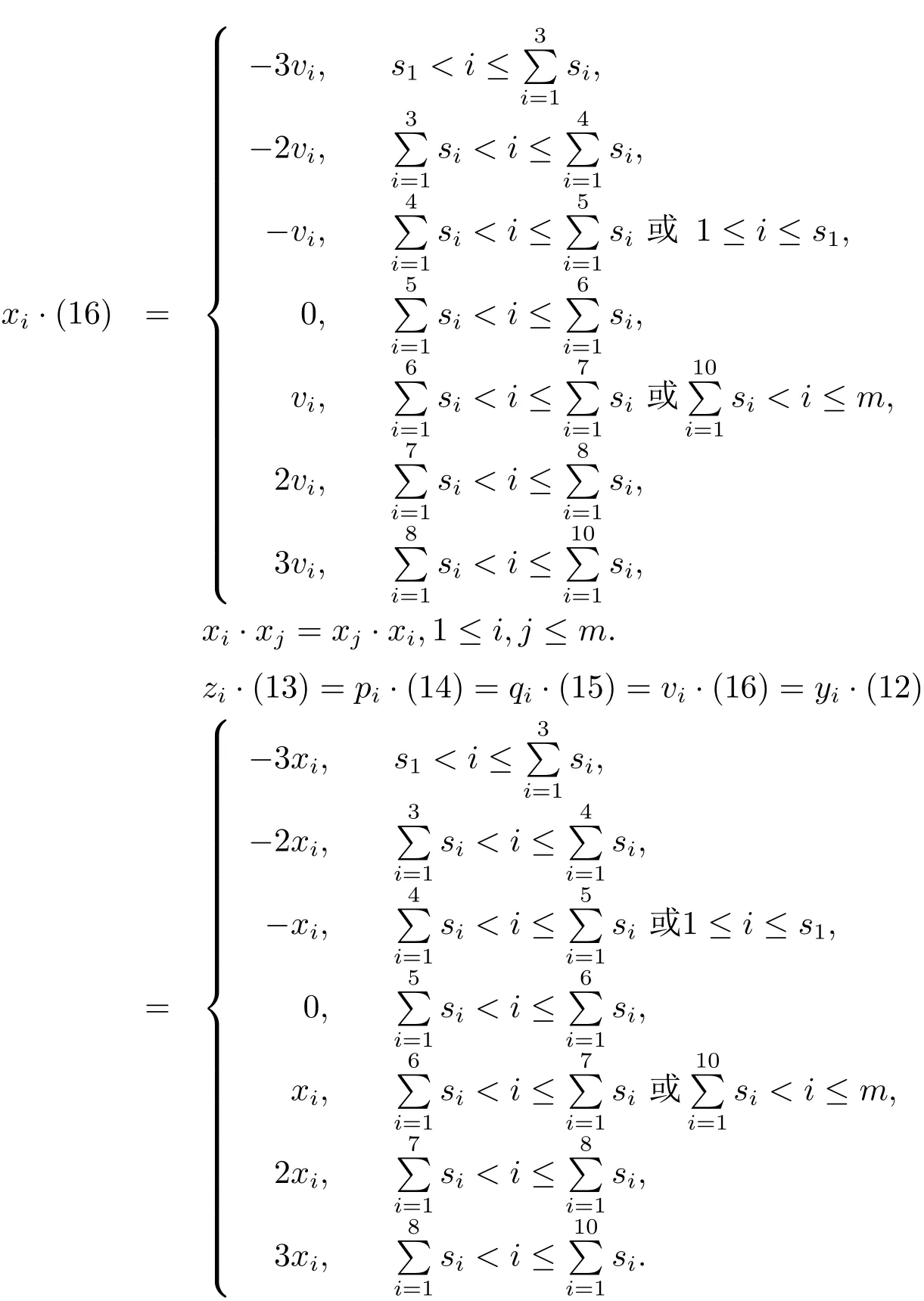
余代數(shù)結(jié)構(gòu)為Δ((1t))=((1t))?((1t)),ε((1t))=1,S((1t))=(1t),t=2,3,4,5,6,Δ(w)=(1)?w+w?(1),ε(w)=0,S(w)= ?w,這里w=xi,yi,zi,pi,qi,vi,而

證 由文獻(xiàn)[15]中一型路代數(shù)的乘法關(guān)系,經(jīng)過計算,容易得出上述所有關(guān)系.

