Pull-in Instability Analysis of Nanoelectromechanical Rectangular Plates Including the Intermolecular, Hydrostatic, and Thermal Actuations Using an Analytical Solution Methodology
F.Samadani, R.Ansari,K.Hosseini, and A.Zabihi
1Department of Mechanical Engineering, University of Guilan, P.O.Box 3756, Rasht, Iran
2Department of Mathematics, Rasht Branch, Islamic Azad University, Rasht, Iran
3Department of Mechanical Engineering, Ahrar Institute of Technology & Higher Education, Rasht, Iran
(Received May 10, 2018; revised manuscript received August 21, 2018)
Abstract The current paper presents a thorough study on the pull-in instability of nanoelectromechanical rectangular plates under intermolecular, hydrostatic, and thermal actuations.Based on the Kirchhoff theory along with Eringen’s nonlocal elasticity theory, a nonclassical model is developed.Using the Galerkin method (GM), the governing equation which is a nonlinear partial differential equation (NLPDE)of the fourth order is converted to a nonlinear ordinary differential equation (NLODE)in the time domain.Then, the reduced NLODE is solved analytically by means of the homotopy analysis method.At the end, the effects of model parameters as well as the nonlocal parameter on the deflection, nonlinear frequency, and dynamic pull-in voltage are explored.
Key words: Nanoelectromechanical rectangular plates,Pull-in instability,Kirchhoff theory,Eringen’s nonlocal elasticity theory, Homotopy analysis method
1 Introduction
Numerous applications of micro- and nano-electromechanical systems (MEMS/NEMS)have motivated researchers to study their performance in various situations.Because the classical continuum theories cannot consider the size effects in the mechanical analysis of nanostructures,[1?4]some size-dependent continuum theories like Eringen’s nonlocal elasticity theory,[5]the couple stress elasticity theory,[6]the Gurtin-Murdoch continuum elasticity theory,[7?11]the strain gradient elasticity theory,[12]and the stress-driven nonlocal model[13]were proposed to consider the size effects.In the classical theories, the stress state at a given point is determined only by the strain state at that point, but in Eringen’s nonlocal elasticity theory, the stress state at a given point is determined by the strain states of all points in the body.The first use of Eringen’s nonlocal elasticity theory to nanotechnology was proposed by Peddiesonet al.,[14]followed by many other researchers.[15?19]One of the important designing considerations in MEMS/NEMS is the pull-in instability.[20]The pull-in instability happens when the internal and applied external forces surpass the elastic restoring force of the nanostructures, leading to contact between the movable and substrate electrodes.When the rate of applied voltage variation is significant,the effect of inertia is considered.In this case, the pull-in instability is referred to as the dynamic pull-in instability.
Once the space of movable and bottom electrodes is less than the plasma wavelength or the absorption wavelength of the ingredient material of surfaces, the intermolecular force is considered as the van der Waals (vdW)attraction.In this situation, there is a small separation regime such that the vdW force is the dominant attraction and it is proportional to the inverse cube of the separation.Nevertheless, when the separation is adequately large (typically above 20 nm)the intermolecular interaction is referred to as the Casimir force.[21]In this case,there is a large separation regime in which the Casimir force is dominant(typically above several tens of nanometers)and it is proportional to the inverse fourth power of the separationπ2hc/240g4, in whichh=1.055×10?34is Planck’s constant divided by 2πandc=2.998×108m/s is the speed of light.[21]The reader is referred to Refs.[22–30]as some important papers and books about the Casimir effect.One of the most remarkable predictions of quantum electrodynamics (QED), obtained by Casimir in 1948, is that two parallel, closely spaced, conducting plates will be mutually attracted.[31]This measurement, as reported by Sparnaay in 1958, confirmed the formula.[32]A closely related effect, the attraction of a neutral atom to a conducting plate, has been also measured.[33]
In the past few years, many researchers have focused on the pull-in instability of nanoplates.For instance, based on a modified continuum model, Ansariet al.[34]studied the size-dependent pull-in behavior of electrostatically and hydrostatically actuated rectangular nanoplates considering the surface stress effects.Ebrahimi and Hosseini[35]investigated the effect of temperature on pull-in voltage and nonlinear vibration of nanoplatebased NEMS under hydrostatic and electrostatic actuations.Mirkalantariet al.[36]studied the pull-in instability of rectangular nanoplates based on the strain gradient theory taking the surface stress effects into account.Shokravi[37]analyzed the dynamic pull-in of viscoelastic nanoplates under the electrostatic and Casimir forces.The interested reader is referred to Refs.[38–44].
Moreover,different methods have been used for the vibration analysis of rectangular nanoplates.For example,Aghababaei and Reddy[45]presented the Navier solutions for the vibrations of rectangular plates based on the nonlocal third-order shear deformation plate theory.Also,Pradhan and Phadikar[46]used the same solution technique for addressing the vibration problem of rectangular plates with simply-supported boundary conditions in the context of Eringen’s nonlocal model,the classical and firstorder shear deformation plate theories.Another application of the Navier-type method to the vibration problem of nonlocal plates can be found in Ref.[47].Aksencer and Aydogdu[48]employed the Levy-type solution method for the vibration analysis of nanoplates based on the nonlocal elasticity theory.Ansariet al.[49?50]used the generalized differential quadrature method to numerically solve the free vibration problem of rectangular Mindlin-type plates with various boundary conditions.The Galerkin method was applied by Shakouriet al.[51]for the vibrational analysis of nonlocal Kirchhoff plates with different edge supports.
The classical analytical methods cannot handle the strongly nonlinear differential equations.In this regard,Liao[52]developed an efficient technique called the homotopy analysis method (HAM), which can be adopted for solving ordinary and partial differential equations with different nonlinearities.For example, Samadaniet al.[53]applied HAM for the pull-in and nonlinear vibration analysis of nanobeams using a nonlocal Euler-Bernoulli beam model.Moghimi Zand and Ahmadian[54]used HAM in studying the dynamic pull-in instability of microsystems.Also, Miandoabet al.[55]utilized this method for the forced vibration analysis of a nano-resonator with cubic nonlinearities.
In the present paper, HAM is used to study the static and dynamic pull-in instabilities of rectangular nanoplates using the nonlocal Kirchhoff plate theory.The rest of paper is organized as follows: In Sec.2,using Eringen’s nonlocal elasticity and the Kirchhoff plate theory, the nonlinear equation of motion subjected to fully clamped boundary condition (CCCC)is derived.In Secs.3 and 4, the governing equation of motion is reduced to an NLODE in the time domain by the Galerkin method.Then, HAM is adopted to solve the obtained nonlinear equation.The effects of intermolecular, hydrostatic, and thermal actuations as well as the nonlocal parameter on the deflection,nonlinear frequency, and the critical voltage of dynamic pull-in instability (Vpdyn)are investigated in Sec.5.At the end, the main findings of the paper is given in Sec.6.
2 Problem Formulation
2.1 Nonlocal Elasticity Theory
Based on Eringen’s nonlocal elasticity theory,[3]the stress at a reference point depends on the strain at all points in the body.The constitutive equation of the nonlocal elasticity can be written as
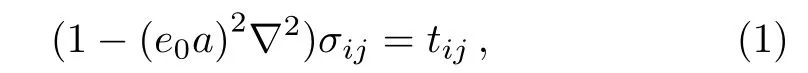
whereσij,tij,e0,andaare the nonlocal stress tensor,the classical stress tensor, nonlocal elasticity constant appropriate to each material and internal characteristic length scale (e.g.atomistic distance), respectively.e0can be obtained from experiments or through comparisons between the results of nonlocal continuum model and the ones from lattice dynamics.Eringen[3]estimated the value ofe0equal to 0.31 based on the comparison of Rayleigh surface wave using the nonlocal theory and lattice dynamics.Whene0is zero,the constitutive relations of the local theories are obtained.Also,?2is the Laplacian operator which in the Cartesian coordinate can be expressed as
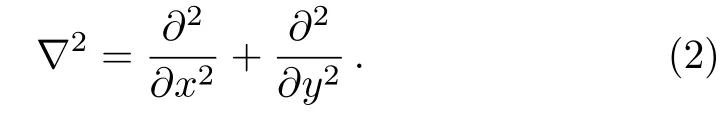
2.2 Kirchhoff Thin Plate Theory
Based on the Kirchhoff thin plate theory, the strains in the plate are
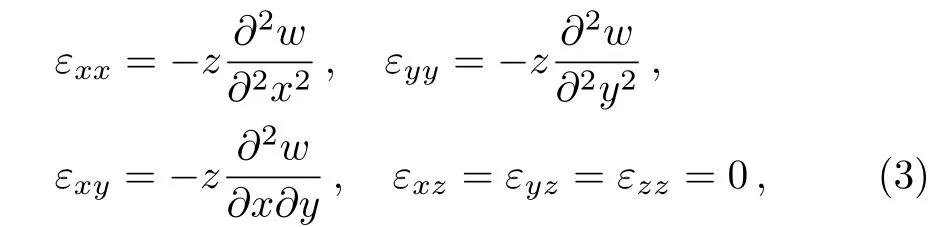
wherewis the transverse deflection of plate, respectively.The relations of bending moment are given by
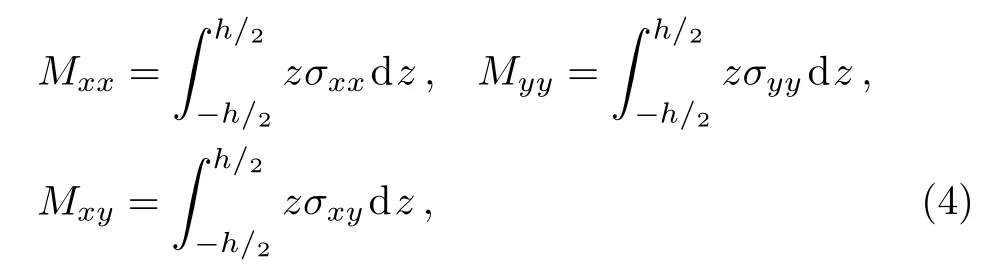
wherehis the thickness of plate.
Under plane stress conditions, one has
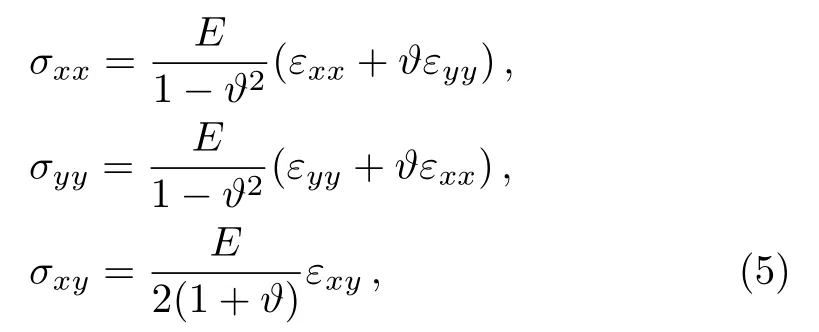
where?andEare Poisson’s ratio and Young’s modulus of the plate.By substituting Eqs.(3)and(5)into Eq.(4),one obtains
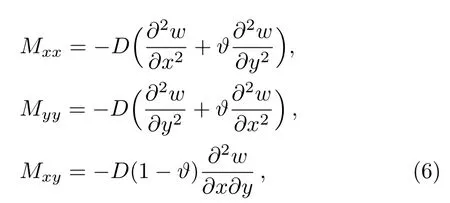
whereD=Eh3/12(1??2)is the classical bending stiffness of the plate.By inserting Eqs.(1)and (4), one can arrive at
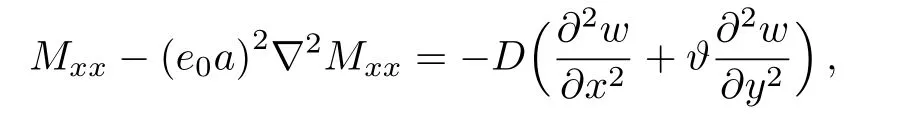
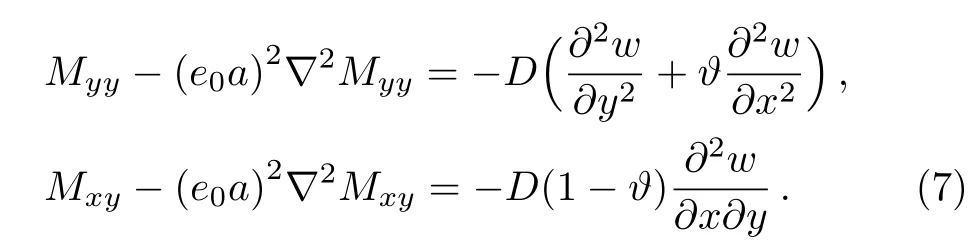
Hamilton’s principle is given in the following form
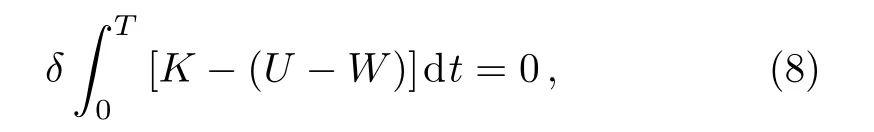
whereK,U, andWdenote the kinetic energy, strain energy and work of external forces and thermal actuation,respectively.The first variation of strain energy is presented as
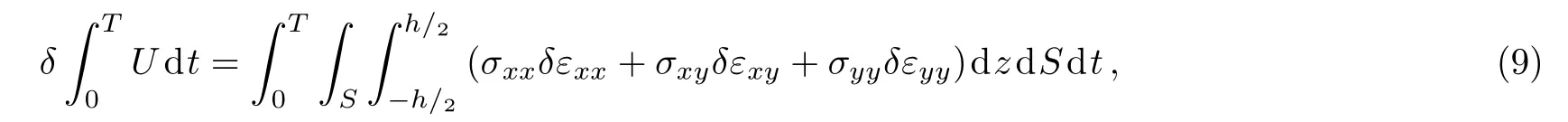
in whichSsignifies the area of plate.The first variation of the work of the external forces and thermal actuation is expressed as

where the termsNxx,Nyy,Nxy,andqare determined by the thermal and external forces.It should be mentioned that the thermal force caused by the uniform temperature variation,θ=T ?T0, is described by[56]

where the termαindicates the coefficient of thermal expansion.
The first variation of kinetic energy is
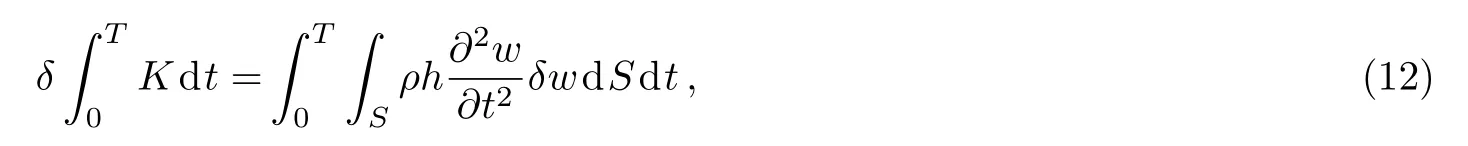
in whichρshows the density of plate.
By inserting Eqs.(9)–(12)in Eq.(8), then integrating by parts and setting the coefficientδwto zero, one can reach the governing equation as
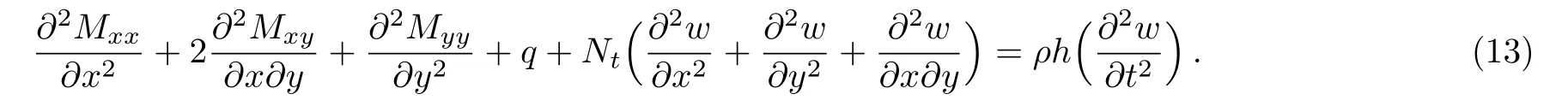
Now, by means of the nonlocal bending moment equations given in Eq.(7)and expanding Eq.(13), one will arrive at the governing equation of motion in the following form
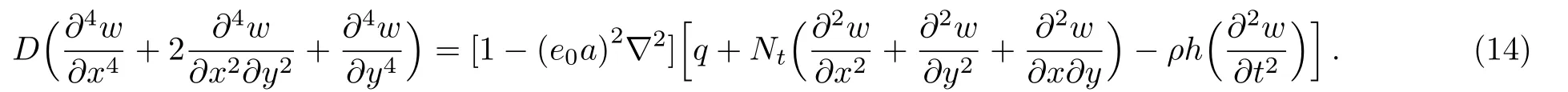
Note that the governing equation of local model is obtained by settinge0a=0.
3 Mathematical Modeling of the Problem
A schematic of nanoelectromechanical rectangular plate with lengthlaand widthlb, including a pair of parallel electrodes with the distancegis given in Fig.1.The upper movable electrode is assumed to be under the influence of intermolecular, hydrostatic, and thermal actuations.
It is noted that the movable electrode pulls down the fixed electrode by applying the DC voltage between two electrodes.Once the applied voltage approaches the critical point (pull-in voltage), the structure becomes unstable.[57]
The electrostatic force per unit area of nanoplate can be described as[39]
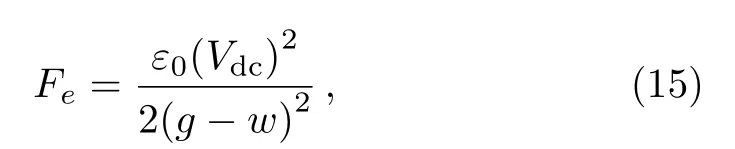
whereε0=8.854×10?12C2N?1·m?2is the vacuum permittivity,gis the air initial gap of nanoplates, andVdcis the direct current voltage as illistrated in Fig.1.The van dar Waals effect per unit area of nanoplate can be written as[39]

whereAhis the Hamaker constant in the range of [0.4?4]×10?19.

Fig.1 Schematic of fully clamped nanoelectromechanical rectangular plates under intermolecular, hydrostatic and thermal actuations.
In the following analyses, it is assumed that

whereFhstands for the hydrostatic actuation.By substituting Eqs.(15)and (16)into Eq.(17)and then inserting the resulting equation in Eq.(14),the following governing equation of motion is obtained

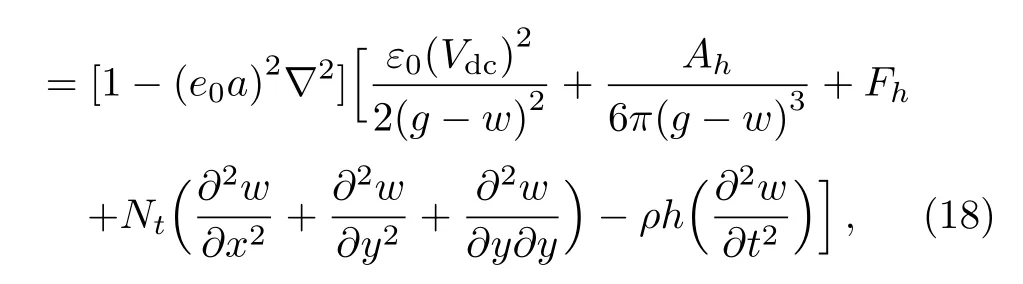
with the following fully clamped boundary conditions
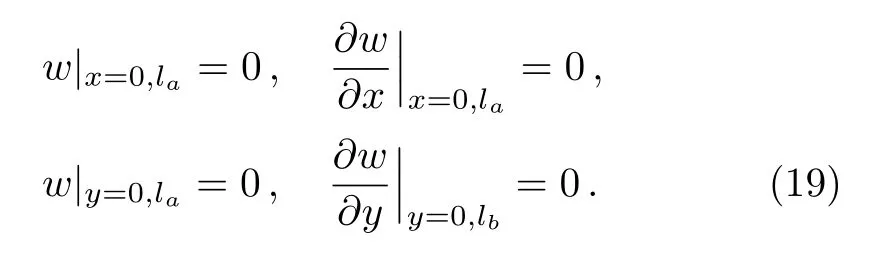
By considering the following nondimensional variables
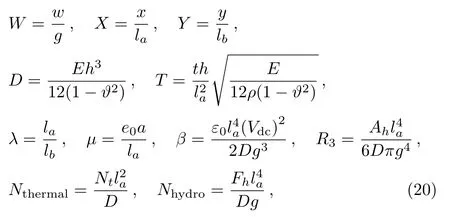
and using the Taylor expansion(see Appendix),the nondimensional form of governing equation can be derived as

with the following boundary conditions
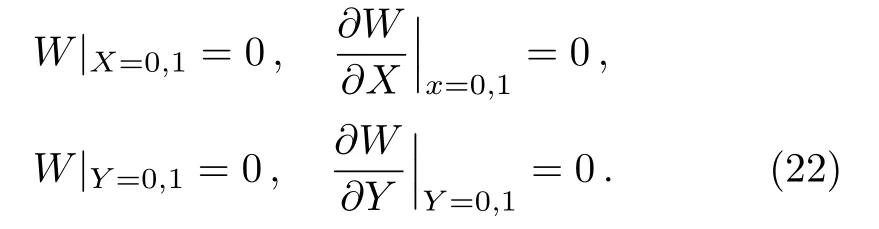
Here,GM is utilized to reduce Eq.(21)to an NLODE.To this end, it is considered that
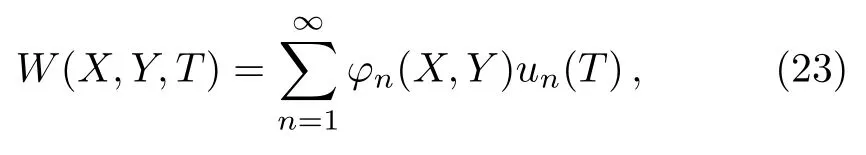
whereφ1(X,Y)= sin2(πX)sin2(πY)is the first eigenmode of fully clamped nanoplate andW1(X,Y,T)=u(T)sin2(πX)sin2(πY).[58]
By insertingW1(X,Y,T)in Eq.(21),multiplying it byφ1(X,Y)and then integrating twice from zero to one, the following NLODE is obtained

where the parametersa0,a1,a2,a3,a4, andMare given in Appendix.
4 Implementation of the HAM to the Reduced Equation
Now, using the transformationτ= ?pT, the existing reduced problem

is changed into
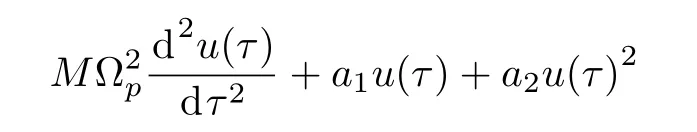
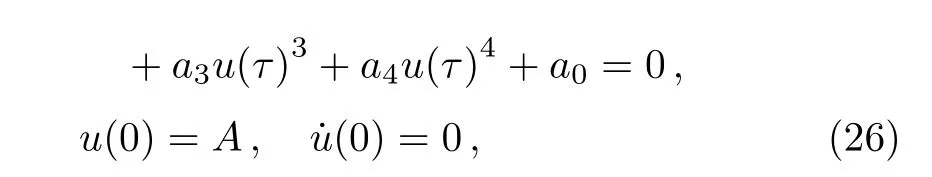
where the oscillation nonlinear frequency ?pis expressed as

In a manner similar to that performed in Ref.[53],one can obtain ? andu(T)for vibrating actuated fully clamped nanoplate as below

5 Results and Discussion
The current section provides numerical results to show the effects of intermolecular, hydrostatic, and thermal actuations as well as the nonlocal parameterμon the deflection, nonlinear frequency, andVpdyn.For producing the results, the following parameters are selected:h=21 nm,la=lb=30h,g=1.2h,?=0.35, andE=68.5 GPa (Al alloy).
In Fig.2,the nondimensional center point deflection of nanoplate obtained using HAM is compared to that calculated using the Runge-Kutta method.It is seen that there is an excellent agreement between the results of two methods.
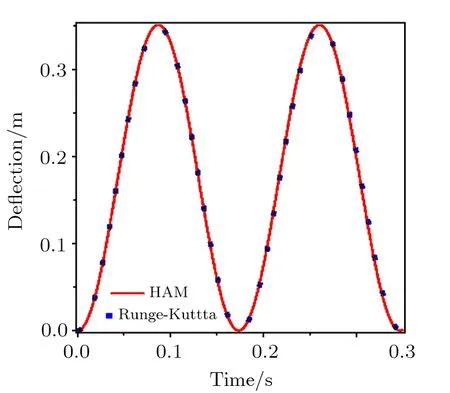
Fig.2 HAM results versus those of the Runge-Kutta method.
Figure 3 shows the change in amplitude of vibration against the nondimensional time.In this case, the dynamic pull-in voltage is 22.540.TheVpdynobtained in the absence of the intermolecular and thermal parameters agrees well with those reported in Refs.[34, 59] (in Ref.[34]Vpdyn= 22.5 and in Ref.[59]Vpdyn= 22.38).The amplitude enhances with the increase of time and the nanoplate experiences a harmonic motion.Also, the nanoplate collapses onto the bottom, when the pull-in happens.
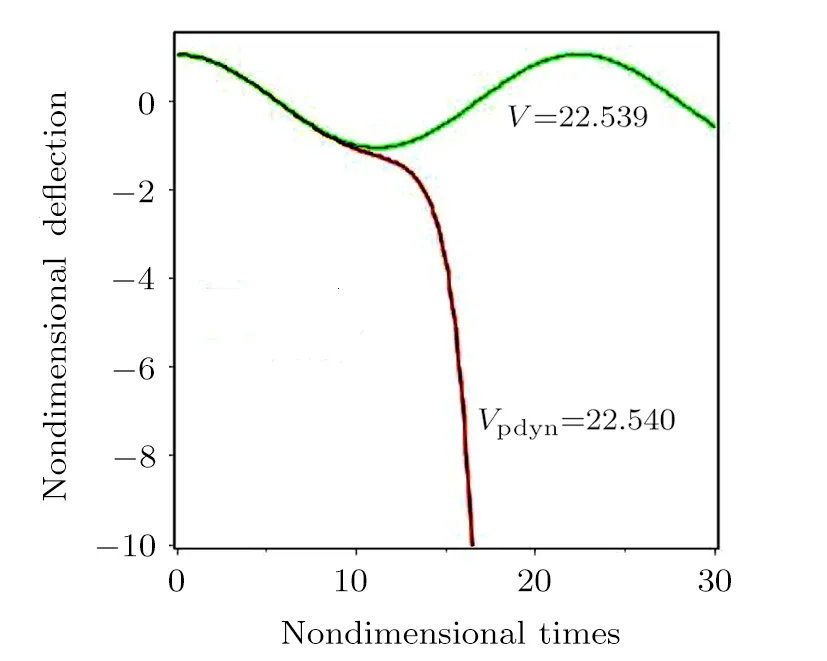
Fig.3 Centerpoint deflection of a fully clamped nanoplate at Nthermal=R3=0.
Figure 4 presents the normalized fundamental frequency of nanoplate with respect to the electrostatic parameterβ.It is observed that the normalized fundamental frequency becomes zero when the applied voltage reachesVpdyn.
Figure 5 indicates that the pull-in time decreases (11 percent)by increasingμ(0.01 per unit).By decreasingμ,the pull-in phenomenon occurs later in this model.
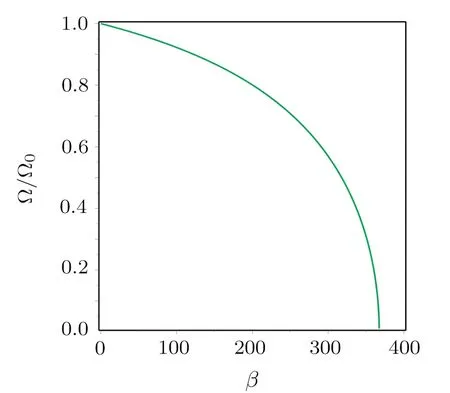
Fig.4 Relation between the normalized fundamental frequency and the electrostatic force parameter.
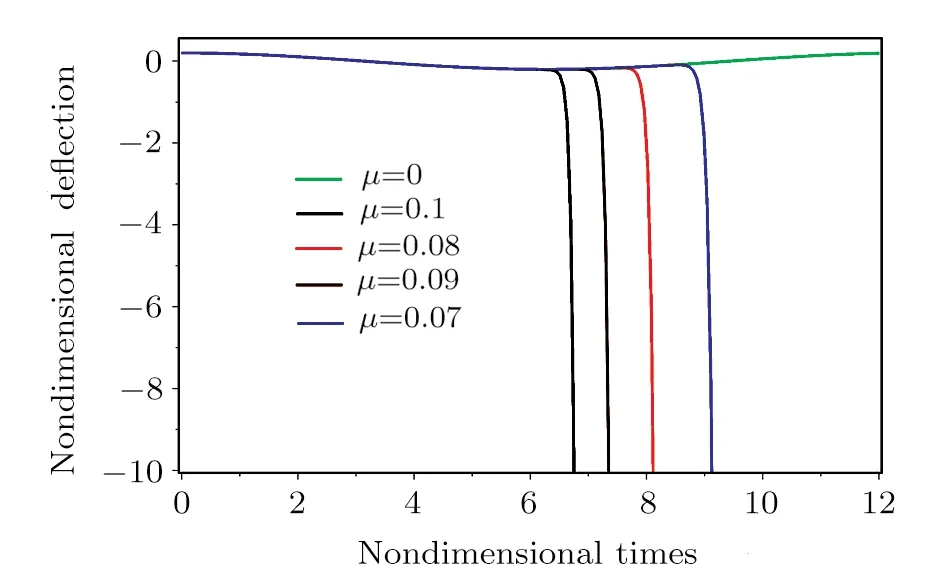
Fig.5 Effect of the parameter μ on the pull-in and deflection time.
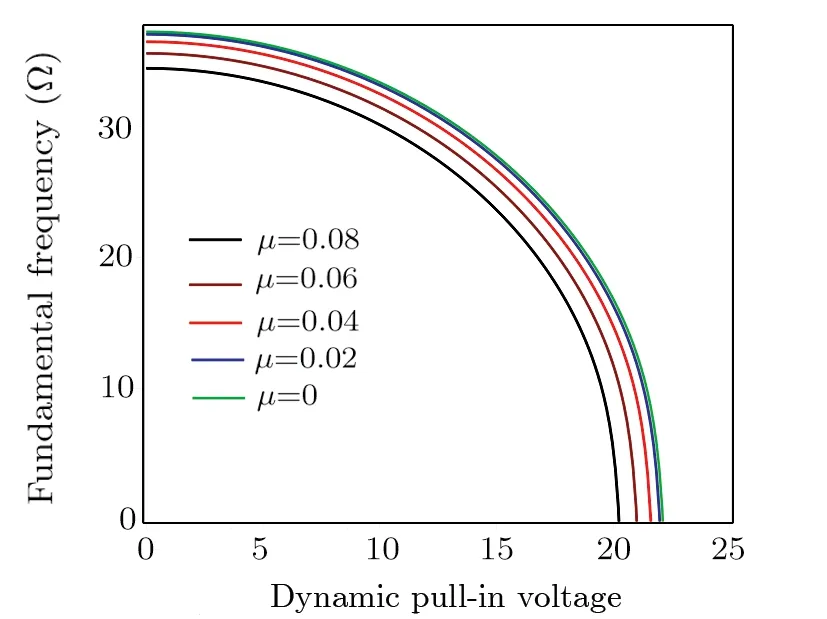
Fig.6 Effect of the parameters μ and Vpdyn on the fundamental frequency.
The variations of fundamental frequencies againstVpdynare illustrated in Fig.6 for different values of nonlocal parameter.It is observed that by increasingμ(0.02 per unit), the fundamental frequency decreases (2 percent).For example,whenμis considered to be 0.06,Vpdynoccurs at 21.
Figure 7 demonstrates the variations of fundamental frequencies against the hydrostatic pressure parameter for different values of nonlocal parameter.The increase ofNhydroleads to the decrease of fundamental frequency.
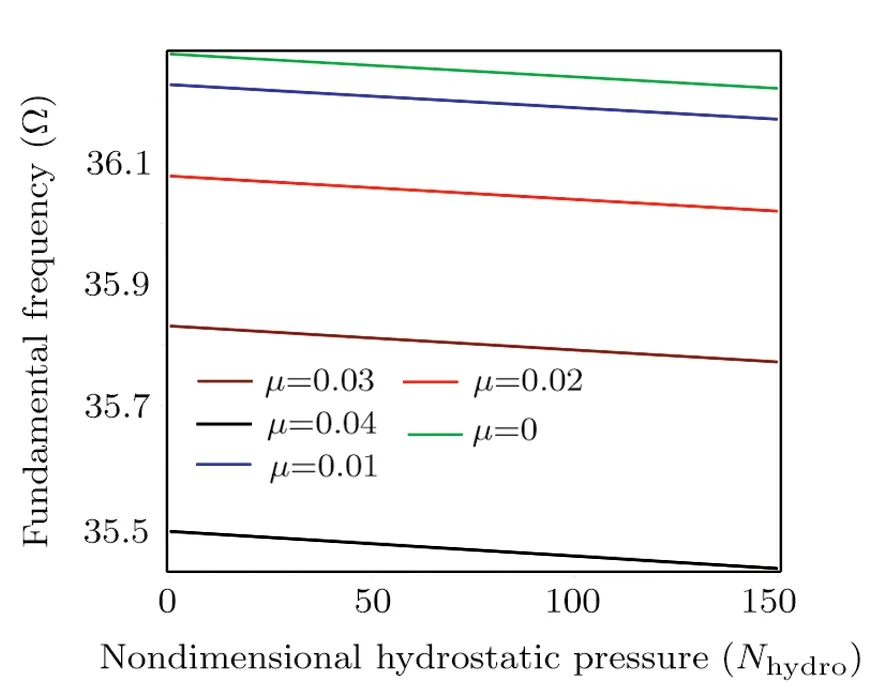
Fig.7 Effect of the nondimensional hydrostatic pressure on the fundamental frequency.
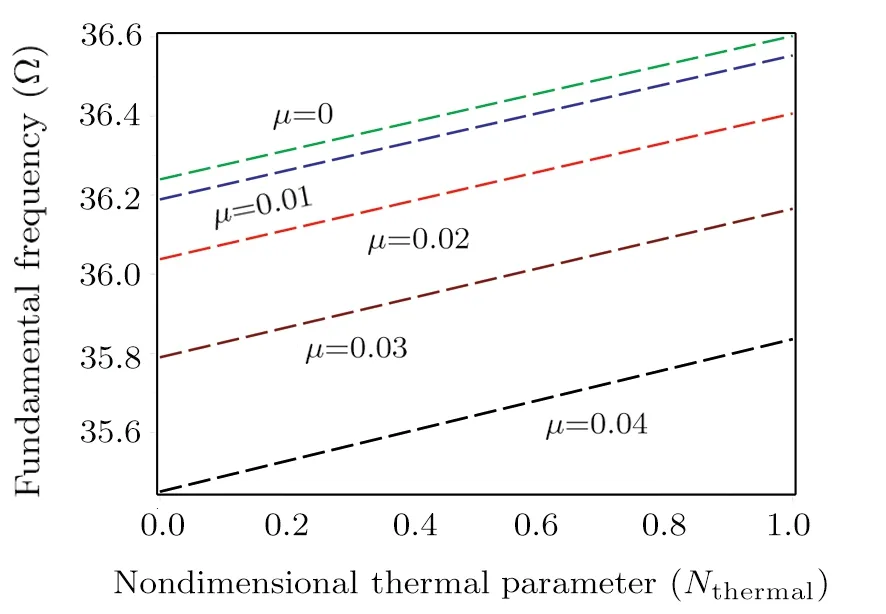
Fig.8 Effect of the nondimensional thermal actuation on the pull-in frequency.
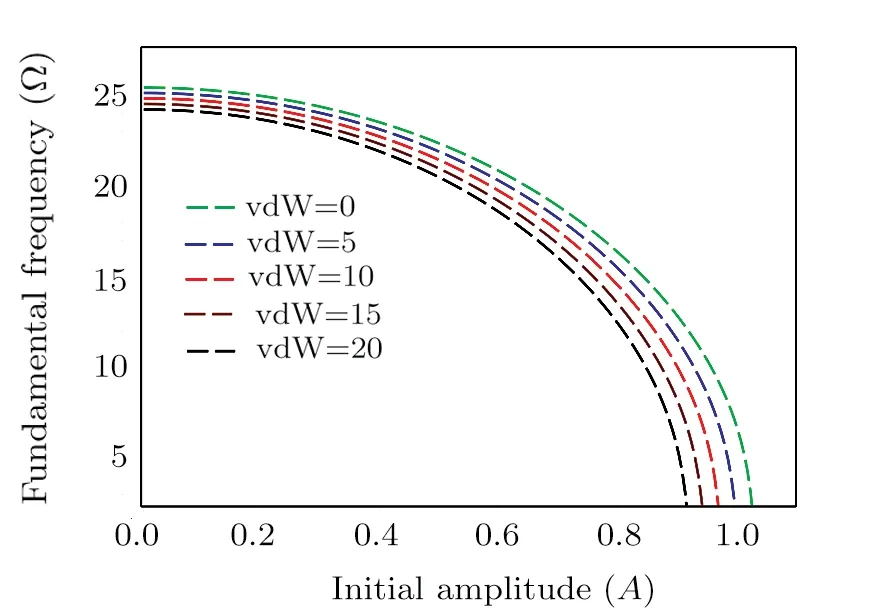
Fig.9 Effect of the intermolecular actuation on the pull-in frequency.
The variations of fundamental frequencies against the nondimensional thermal parameter are illustrated in Fig.8 for various values ofμ.One can find that via increasingNthermal, the fundamental frequency gets larger.
Figure 9 shows the variations of fundamental natural frequency versusAfor a number of vdW parameters.It is seen that by increasingA, the nonlinear frequency of vibration diminishes.For instance, whenR3is equal to 5,the pull-in phenomenon happens atA=1.
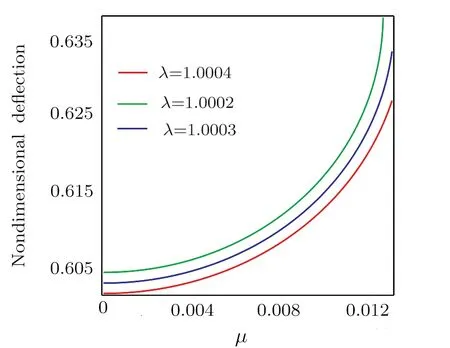
Fig.10 Variations of static pull-in deflection of the nanoplate versus the μ.
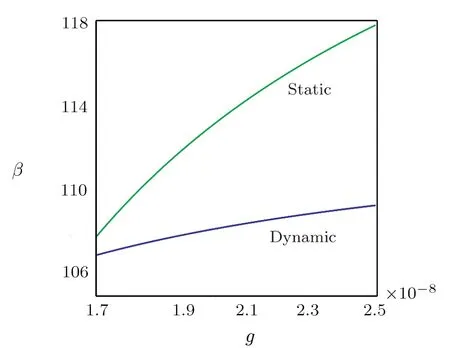
Fig.11 Comparison of the static and dynamic pullvoltage parameter versus g in μ=0.01.
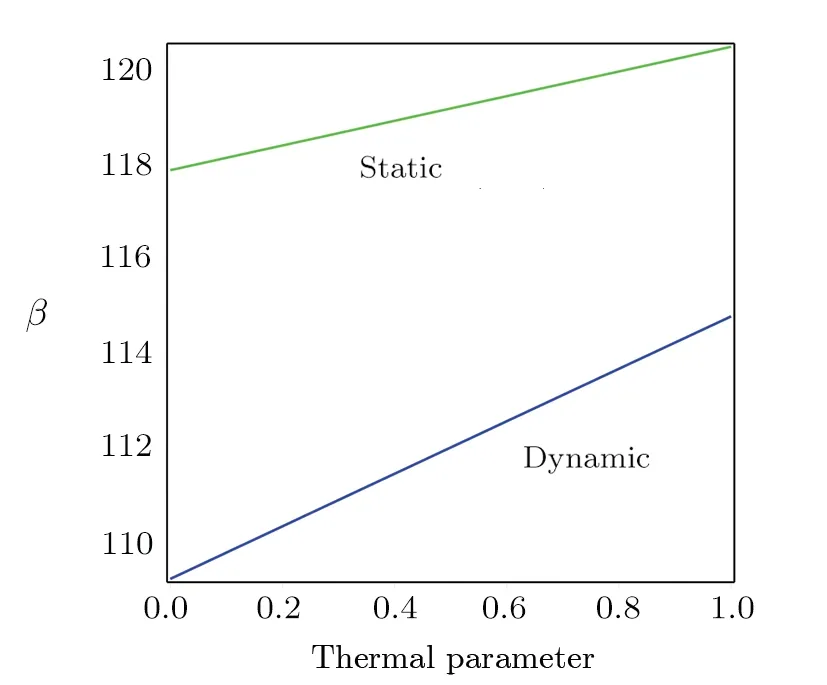
Fig.12 Evaluation of the static and dynamic pullvoltage against Nthermal in μ=0.01.
The influence ofla/lbon the static nondimensional deflection versus the nonlocal parameter is highlighted in Fig.10.According to this figure, the pull-in instability is suspended asλincreases.The influences of distance of parallel electrodes, thermal and nonlocal parameters on the static and dynamic pull-in voltage parameter are compared in Figs.11–13, respectively.Based on Fig.11,the pull-in voltage is postponed as the distance increases.Also, Fig.12 indicates that as the thermal parameter increases, the pull-in voltage is delayed.Finally, Fig.13 shows that by increasing the nonlocal parameter,the pullin voltage decreases.
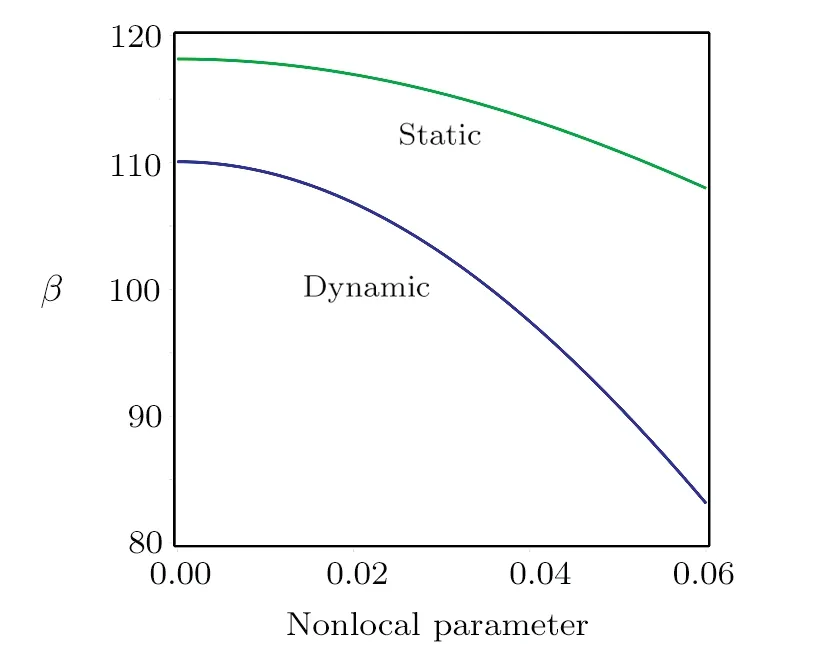
Fig.13 Comparision of dynamic and static pull-in voltage parameter of the nanoplate versus the μ.
6 Conclusion
In the present research, the dynamic pull-in of CCCC plate-type nanosensor, subjected to electrostatic, intermolecular, hydrostatic and thermal actuations was analyzed based on the nonlocal theory.GM was utilized for reducing the governing NLPDE to an NLODE in the time domain.HAM was also applied for solving the NLODE.The outcomes reveal that:
(i)By increasingA,Vpdyndecreases.
(ii)With the increase ofμ, vdW, andβ, the fundamental frequency diminishes.
(iii)Vpdyndecreases as the vdW,μ, andAincrease;also, it increases as the thermal and hydrostatic parameters increase.
(iv)? decreases as the pull-in voltage,R3,hydrostatic,nonlocal parameters, andAincrease; but, it increases as the thermal parameter rises.
(v)The softening effect detected qualitatively is in agreement with that in the bending and vibrations of the nonlocal Kirchhoff model.
Appendix
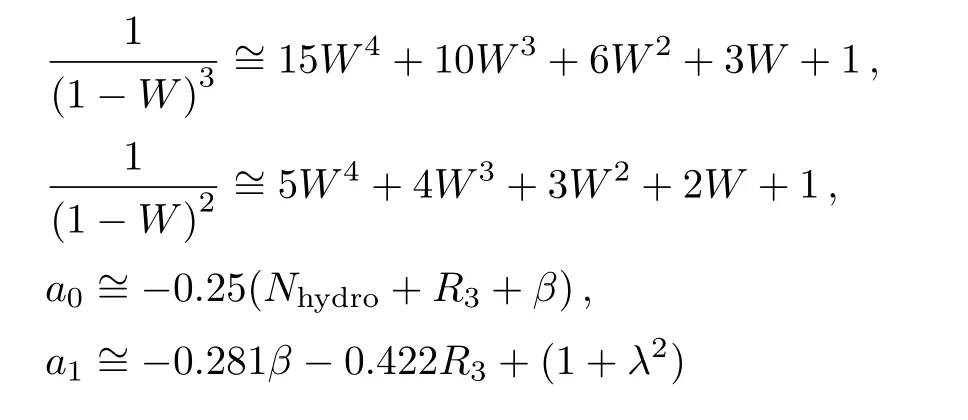
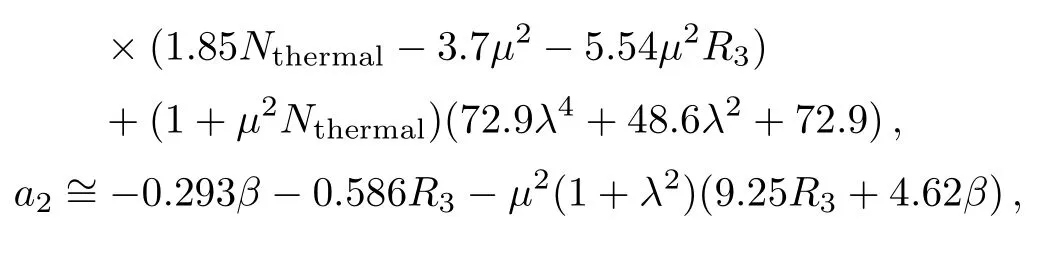

 Communications in Theoretical Physics2019年3期
Communications in Theoretical Physics2019年3期
- Communications in Theoretical Physics的其它文章
- Entropy Quantization of Schwarzschild Black Hole
- Boundary Layer Flow over a Curved Surface Imbedded in Porous Medium
- Spin-Dependent Electron Tunneling in ZnSe/Zn1?xMnxSe Heterostructures with Double δ-Potentials
- Interaction of Wave Trains with Defects?
- Modulated Dust-Acoustic Wave Packets in an Opposite Polarity Dusty Plasma System
- A Modified Gravity Theory: Null Aether?
