DKP Equation with Energy Dependent Potentials
O.Langueur,M.Merad,,?and B.HamilDpartement des sciences de la matre,Facult des Sciences Exactes,Universit de Oum El Bouaghi,04000 Oum El Bouaghi,Algeria
2Dpartement de TC de SNV,Universit Hassiba Benbouali,Chlef,Algeria
(Received March 17,2019;revised manuscript received April 22,2019)
AbstractIn this work,we study the DKP equation subjected to the action of combined vector plus scalar energy depend on potentials in(1+1)dimensions space-time.The conditions of normalisation and continuity equation are calculated.The eigenfunctions and the corresponding eigenvalues are then determined.A numerical study is presented and the energy graphs for some values of the energy parameter are plotted.
Key words:DKP equation,energy dependent potentials,biconf luent Heun function
1 Introduction
For a long time,works on the so called systems with energy dependent potentials[1]have raised a considerable interest because of its varied applications in several areas and their analyses does not cease developing.We quote some examples,the dynamo effect in magneto hydrodynamic models,[2]in quantum wells and semiconductors,[3]including the theory of elastic and inelastic scattering in atomic,nuclear and particle physics,[4?5]and the description of the heavy quark system[6?7]etc.Further,we point out that systems with energy-dependent potentials provide some modifications on the mathematical structure as the scalar product and the completeness relation,necessary to ensure conservation of the norm and satisfy the requirements of quantum mechanics,which has been analyzed clearly in Refs.[6]and[8].
For this purpose,the treatment of the potential dependent energy,continues to increase,consequently numerous works were looked and several methods of analytical and approximate resolution were presented.Let us mention one of these potentials:the harmonic oscillator with an energy-dependent frequency in 1D and in 3D which has recently been solved,[6,9]the Coulomb and the Morse potentials,[10?11]the harmonic oscillator and the Pschl–Teller potential by means of the super symmetry formalism.[12]The D-dimensional Schrdinger and Klein-Gordon equations were studied via the Nikiforov–Uvarov method,[13?14]a class of potentials was perfectly resolvable by the conversion method,[11]the approximate solution of the Dirac equation using the super symmetry quantum mechanics.[15]Dirac particles in the presence of scalar,vector,and tensor potentials have been investigated by using the asymptotic iteration method,[16]extension to the case of systems having mass dependent position were examined in Ref.[17].The harmonic oscillator and the hydrogen atom and the Klein-Gordon particle subjected to vector plus scalar energy dependent potentials were examined by using the Feynman approach.[18?19]The Dirac propagator was determined by using the formalism for super symmetric path integrals[20]and the harmonic oscillator propagator has been constructed via the path integral approach in noncommutative space.[21?22]
In the present paper we extend this idea to the another relativistic equation namely Duffin-Kemmer-Petiau(DKP)equation,other than that of Dirac and Klein-Gordon,describing the dynamics of the scalar and vectorial Bosons.The DKP equation is of great importance of these various applications in quantum chromodynamics,cosmology,gravity,and its richness of these experimentation in areas of physics.[23]To our knowledge,this equation has never been treated with energy-dependent potential,in an analytical manner and its absence is practically noticeable in the context of problems with energy dependent potentials.
In this paper,we will try to study the DKP equation subjected to the action of combined with vector and scalar energy-dependent potentials in(1+1)dimensions space-time on the one hand,and on the other hand to see the effect of this energy dependence on the normal isation conditions and the continuity equation for this system in question.
The outline of this paper is as follows:In Sec.2,we determine the normal is ation condition and continuity equation for(DKP)equation.In Sec.3,we expose an explicit calculation relative to the one-dimensional(DKP)subjected to the action of combined with vector and scalar energy-dependent potentials.By a straightforward calculation,the exact solution is obtained and the energy spectrum and wave functions are deduced.These latter are expressed by the biconf luent Heun polynomials.In Sec.4,a numerical study of the energy function is presented.
2 Normalization Condition and Continuity Equation
The(1+1)-dimensional DKP equation for the scalar and vector bosons moving in a constant electric field and a scalar potential is:
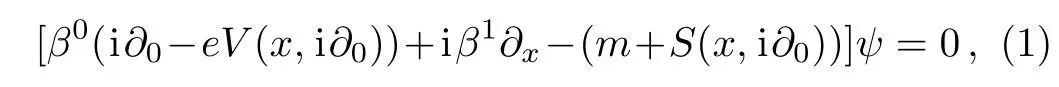
where the matrices β0and β1verify the DKP algebra
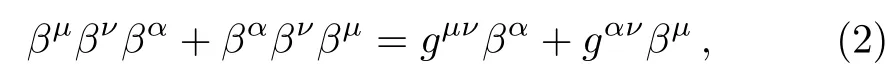
and the potentials V(x,i?0)and S(x,i?0)denote a function of x and energy i?0.
The metric tensor gμν=diag(1?1),and the adjoint spinor=ψ+()verifies the following adjoint equation
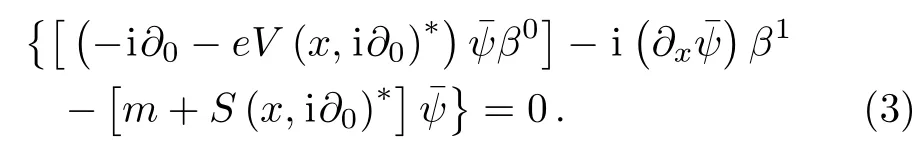
If we expand ψ on the basis{ΦEn}
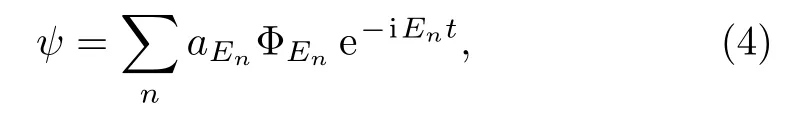
we have
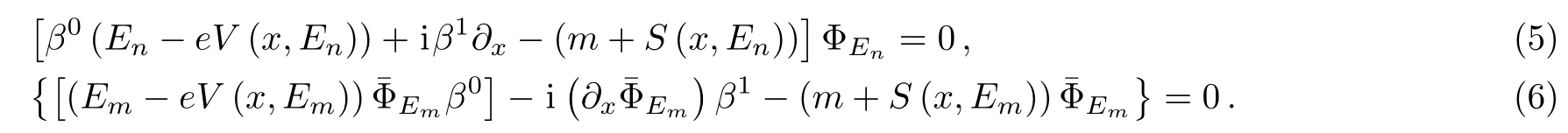
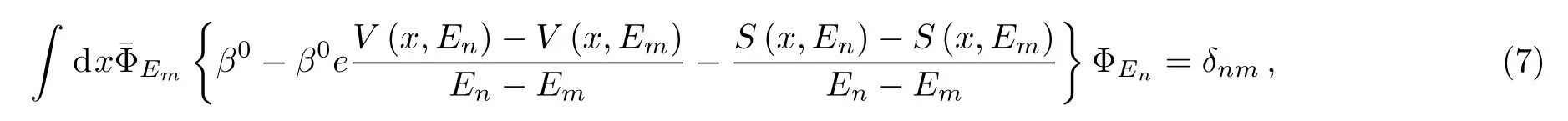
and,in the limit n→m,the above equation becomes

where
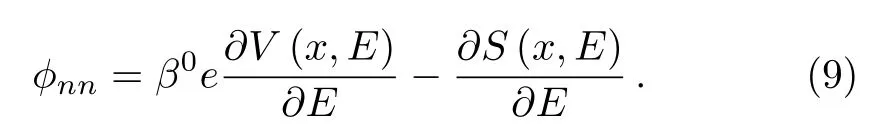
Therefore, the presence of the additional factor{β0??nn}changes the scalar product(the norm).In the case where the potential does not depend on energy ?nn=0,we find the usual normalization condition∫
Now,to derive the continuity equation ?μJμ=multiplying Eq.(1)byand Eq.(3)by(ψ)and differentiating between the two equations,we obtain the following expression
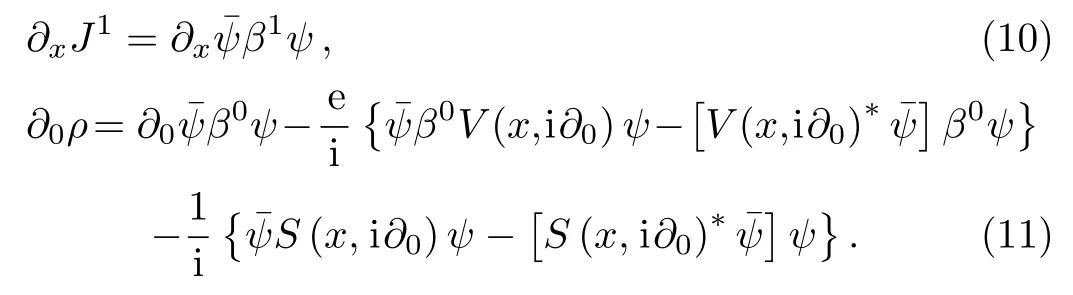
To simplify the form of ρ,we put this separate formed,

After a direct calculation,the expression of the density ρ can be rewritten as
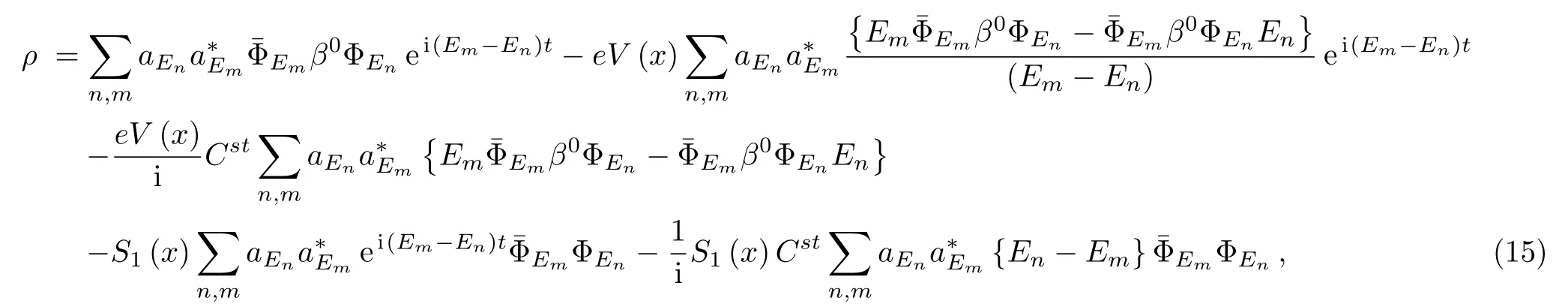
and by taking the lim n→m,Eq.(15)will be reduced to this form
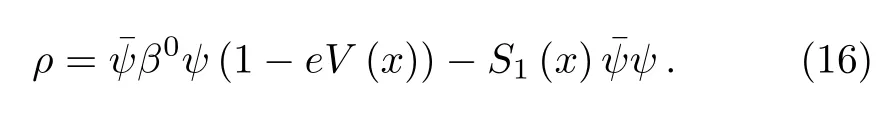
3 DKP Equation in a Constant Electric Field and a Scalar Potential
In this section we illustrate the energy dependent potentials on the energy eigenvalues and eigenfunctions of a DKP particle in a constant electric field and a scalar potential.The electric field and the scalar potential are chosen linear
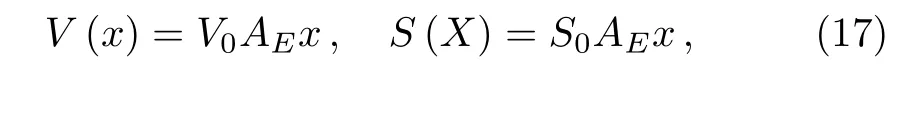
where V0and S0two constants,we suppose|S0|?|V0|to avoid complex eigenvalues,and AE=(1+θE)q.
In(1+1)-dimensional space time,we choose this representation of the following DKP matrix β,
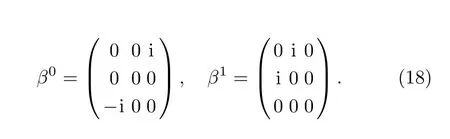
Hence,the DKP equation in the presence of a vector plus scalar with energy dependent potentials is written as
The stationary solution of Eq.(19)has the form ψ(x,t)=?(x)e?iEtand ?(x)is a vectors of dimension(3 × 1)which can be written as
We insert the wave function ? and the matrix β,we obtain the following equations systems
Now,to solve the eigenvalue equation(19),we decouple the system(21)and it is not difficult to verify that ?1satisfies the following Klein Gordon type equation
where

and we introduce the following ansatz
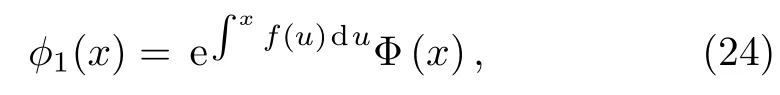
where f(x)is arbitrary function.Then,the equation for Φ(x)is


We choose f(x)to cancel the term(x+(η/μ)),this implies
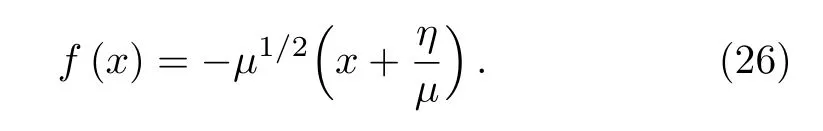
By substituting f(x)with their expression(26)and changing the variable from x to y,by setting y=μ1/4(x+(m/S0AE)),then Eq.(25)can be expressed as
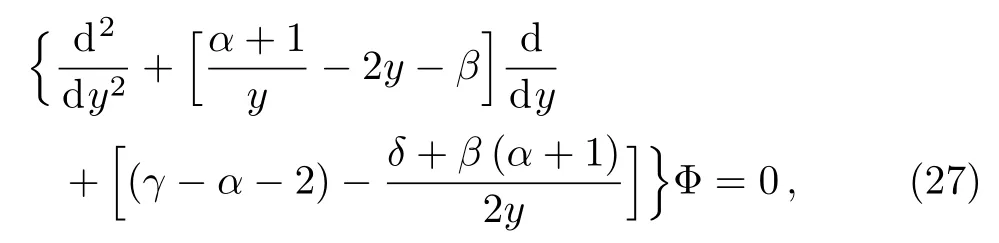
which is exactly the biconfluent Heun differential equation HeunB,[23?24]whose parametersandare given by
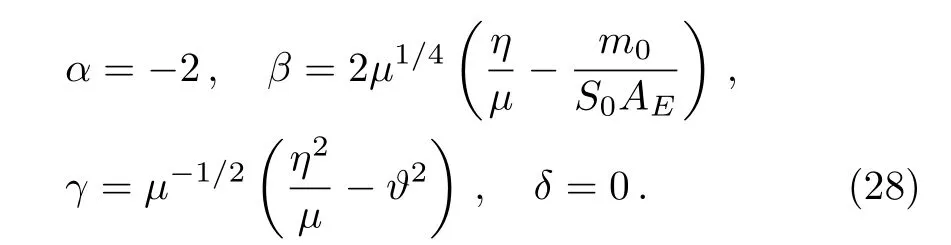
The above differential equation(27)has one regular singularity at the origin(y=0),and one irregular singularity at infinity(y→∞)whose s-rank is R(∞)=3,its solution can be expressed as Eq.(52)(see Appendix):
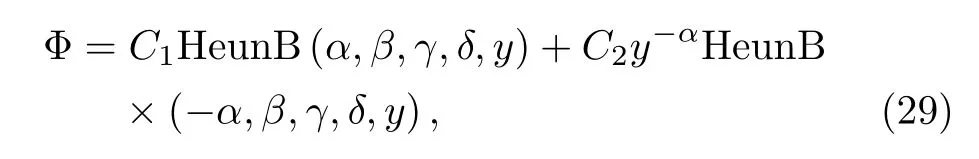
where C1,C2are constant.
The determination of the other components is easy and the final expressions of wave function are as follows:
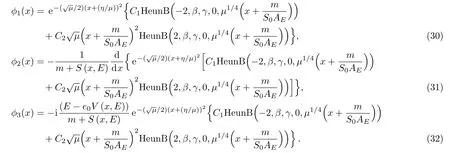
Now,to determine energy spectrum,using the condition(53)(see appendix)and replacing the parametersandby their expressions(28),we finally get the following result
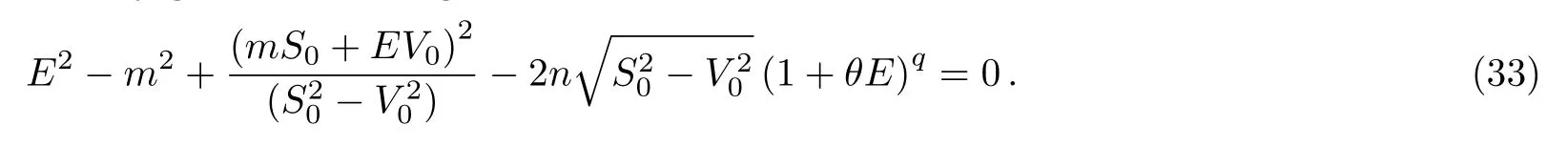
4 Application
Now in our analysis,it is interesting to study two particular cases for values of q,we limit ourselves only to the case q=1 and q=2,for the other cases,the calculation becomes a little more complicated to determine exactly and analytically the values of the spectrum.
(i)First case:q=1:AE=(1+θE),the potentials in Eq.(17)contain a linear energy-dependence,the expression of energy function can be written in the form
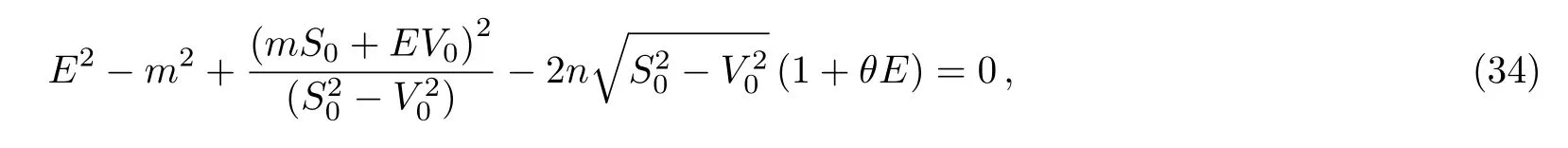
which gives
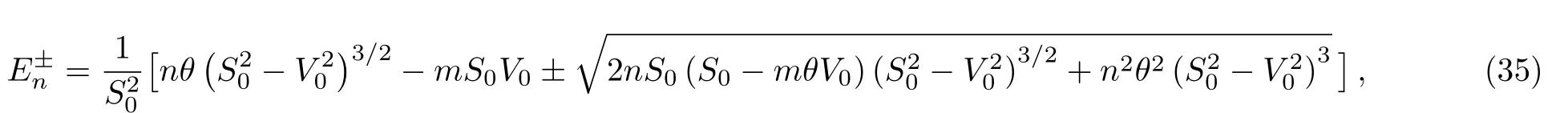
and expanding to the first order in θ,we obtain
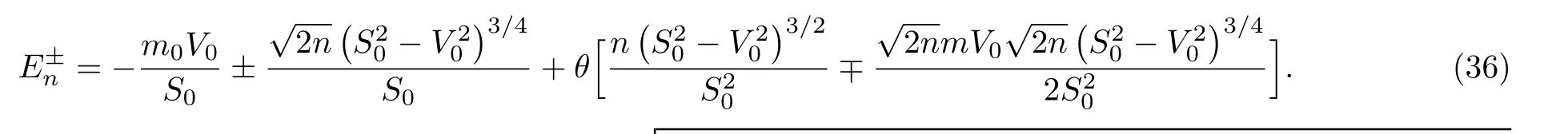
The first term in Eq.(36)is the energy spectrum of the usual DKP equation subjected to the action of combined vector plus scalar and the second term represents the effects of quantum fluctuations of the potential-dependent energy on the system.It is remarkable here that,the expression of the energy spectrum in our system(36)contains an additional deformed correction term depending on the deformation parameter θ and with powers in n due to the dependence of energy potentials.
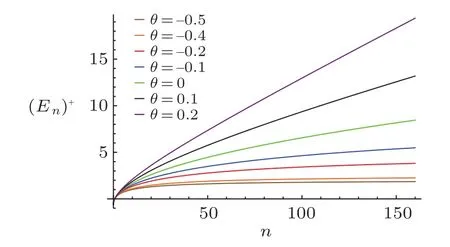
Fig.1(Color online)The plot illustrates the Spectrum of energy(En)+verus quantum number n with V0=0.3,S0=0.5,m=1.
In Fig.1,we notice that:
? For θ negative,the spectrum is compressed and for θ positive,the spectrum is expanded,which produce an increase of the level spacing as a function of n,as the collective states of even–even atomic nuclei in the Bohr–Mottelson model,in particle physics phenomenology and in the physics beyond the standard model,etc.
?It should be noted that,according to the powers in n dependence of the energy levels,it explains confinement at the high energy area.
(ii)Second case:q=2:AE=(1+θE)2,the potentials in Eq.(17)contain a quadratic energy-dependence,the formula of energy simplifies to
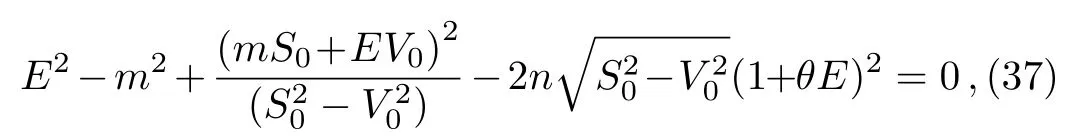
we get
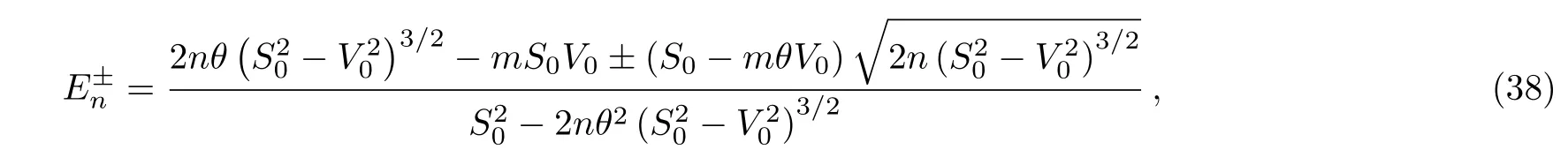
and expanding to the second order in θ,we obtain
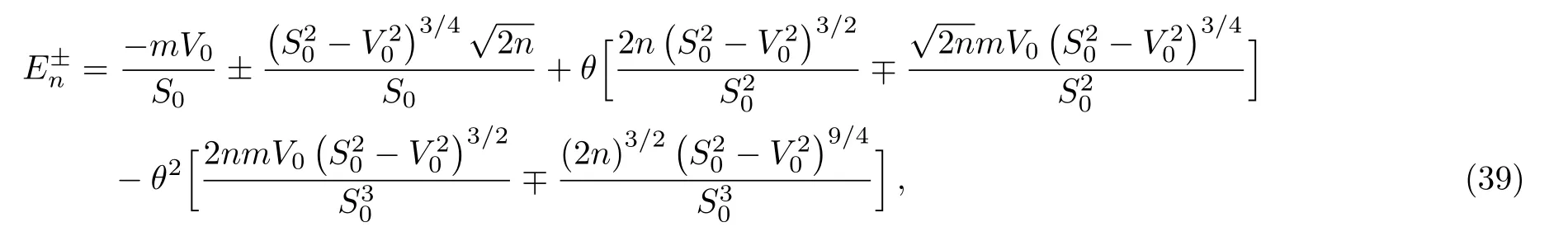
In the end,for the two expressions of energy,in the limθ→ 0 returning to the ordinary case AE=1,we get the usual expression of the energy spectrum of the ordinary DKP equation in the presence of electromagnetic field
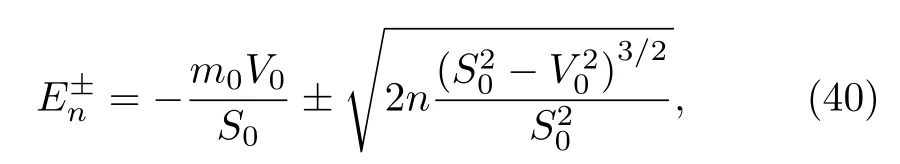
and for S0=V0we see the total disappearance of this energy dependence in Eqs.(35)and(38).
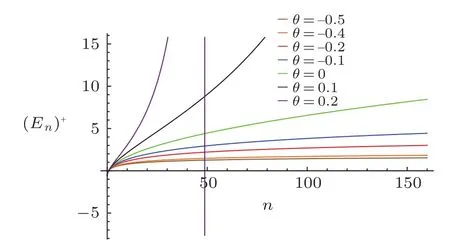
Fig.2 (Color online)The plot illustrates the Spectrum of energy(En)+verus quantum number n with V0=0.3,S0=0.5,m=1.
5 Conclusion
In this contribution,we studied the solutions of the DKP equation subjected to the action of combined vector plus scalar energy depend on potentials in(1+1)dimensions space–time.The conditions of normalisation and a continuity equation were determined and were related to the vector and scalar energy depend on potentials.The wave functions were obtained and were expressed according to the bicon fluent Heun polynomials.The function of the energy was extracted and the particular cases were deduced.A numerical study was presented and the energy graphs were represented for some values of the energy parameter.
Appendix
The “biconfluent Heun equation” (BHE)is a second order linear homogeneous differential equation and it is derived from the general Heun equation by the coalescence of two finite regular singular points with infinity.[24]The canonical form of BHE is generally expressed as
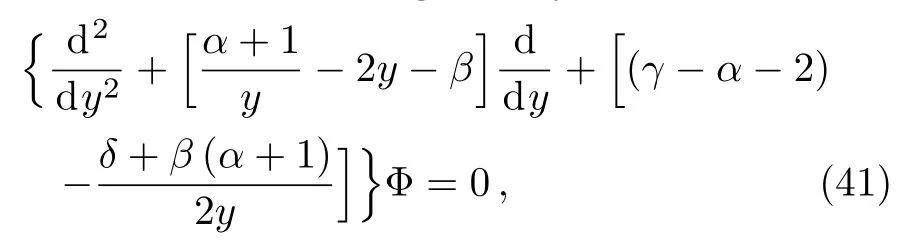
BHE has one regular singularity at the origin(y=0),and one irregular singularity at infinity(y∞)whose s-rank is R(∞)=3.
The Frobenius solution of Eq.(41)in the neighborhood of the regular singular point located at y=0 can be written as the series
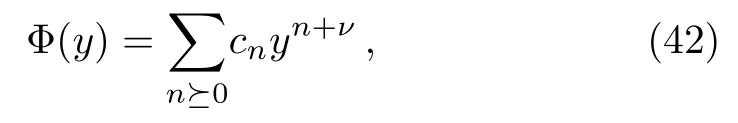
with c0?=0.
Calculating the derivatives from the series(42)term by term yields Φ(y)′, Φ(y)′′and substituting these into Eq.(41),we obtain the conditions

and the three-term recurrence relation
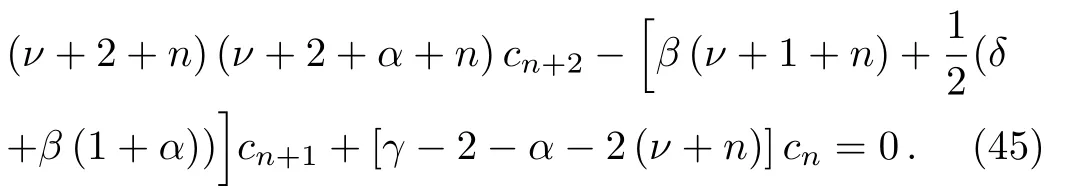
The parameter α not being a negative integer,for ν=0 and c0=1,we can denote the solution by HeunB(),the biconfluent Heun function,defined by the series
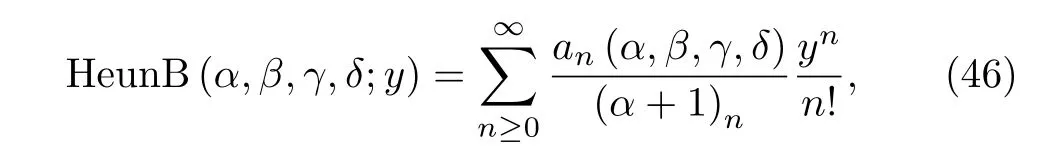
where
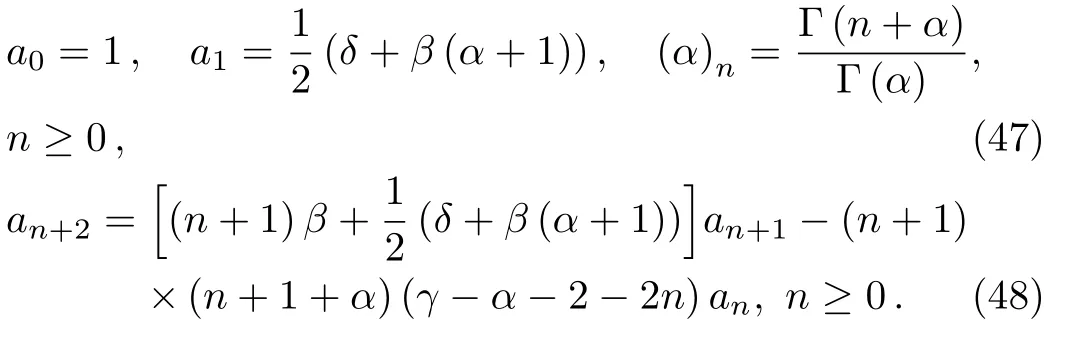
When α is a negative integer(α = ?m,m ≥ 1),it is possible to define
HeunB(?m,β,γ,δ;y)=ymHeunB(m,β,γ,δ;y).(49)If the parameter α is not a relative integer,Eq.(41)admits two solutions that are linearly independent in the neighborhood of the origin,namely
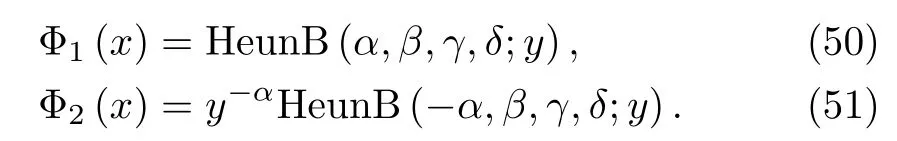
Then the expression of the general solution is given by
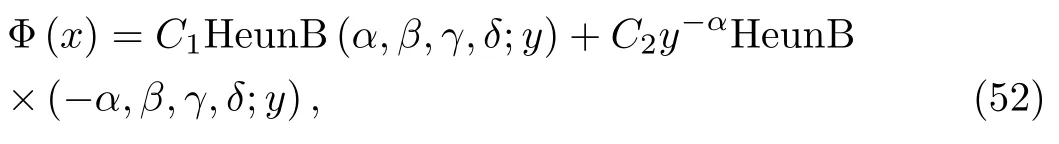
where C1and C2are integration constants and the Wronskian of any two solutions is W= ?αy?(1+α)exp(βy+y2).
From the recurrence relation above,the function HeunB(α,β,γ,δ;y)becomes a polynomial of degree n if and only if the conditions,
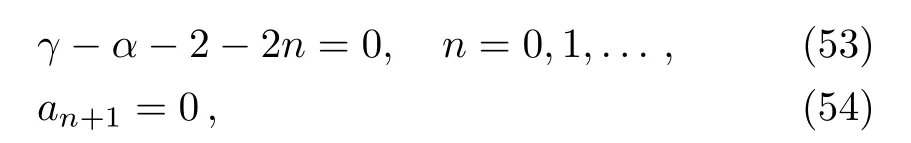
are fulfilled.[24?25]
The solution around the irregular singular point(y∞)is given by the recessive Thome solution.[24,26]However,this solution is not as useful as the solution written near the regular singularity in applications.
We note that BHE is widely involved in different domains of contemporary pure and applied sciences such as quantum mechanics,general relativity,solid state physics,atomic and molecular physics,optical physics and chemistry.[26?27]
Acknowledgements
We wish to thank the referees for their useful comments which greatly improved the manuscript.
 Communications in Theoretical Physics2019年9期
Communications in Theoretical Physics2019年9期
- Communications in Theoretical Physics的其它文章
- Dynamical Analysis and Exact Solutions of a New(2+1)-Dimensional Generalized Boussinesq Model Equation for Nonlinear Rossby Waves?
- Effective Correlation of Two Holes in a Semimagnetic Quantum Well Wire:Influence of Shape of Confining Potential on Coulomb Interaction?
- Scale-Invariance Exists in the Series of Character Intervals in the Four Great Chinese Novels?
- A Statistical Mechanical Analysis on the Bound State Solution of an Energy-Dependent Deformed Hulthn Potential Energy?
- Study on the Amyloid Aβ42 with Accelerated Molecular Dynamics Simulations?
- Inflationary Cosmology with Quantum Gravitational Effects and Swampland Conjectures?
