New Optical Soliton Solutions of the Perturbed Fokas-Lenells Equation
Maha S.M.Shehata,Hadi Rezazadeh, Emad H.M.Zahran, Eric Tala-Tebue, and Ahmet Bekir
1Departments of Mathematics, Zagazig University, Faculty of Science, Zagazig, Egypt
2Faculty of Engineering Technology, Amol University of Special Modern Technologies, Amol, Iran
3Departments of Mathematical and Physical Engineering, Benha University, Faculty of Engineering, Shubra, Egypt
4Laboratoire D’Automatique et D’Informatique Appliquee(LAIA),IUT-FV of Bandjoun, The University of Dschang, BP 134, Bandjoun, Cameroon
5Neighbourhood of Akcaglan, Imarli Street, Number:28/4, 26030, Eskisehir, Turkey
Abstract In this article, we employ the perturbed Fokas-Lenells equation (FLE), which represents recent electronic communications.The Riccati-Bernoulli Sub-ODE method which does not depend on the balance rule is used for the first time to obtain the new exact and solitary wave solutions of this equation.This technique is direct, effective and reduces the large volume of calculations.
Key words:perturbed Fokas-Lenells equation (FLE), Riccati-Bernoulli Sub-ODE method, optical soliton solutions
1 Introduction
The recent electronic communications“Internet blogs,Facebook communication, twitter comments” are all subbranch of the soliton technology.The perturbed Fokas-Lenells equation (FLE)[1?2]that represents this phenomena with the aid of soliton science can be written as
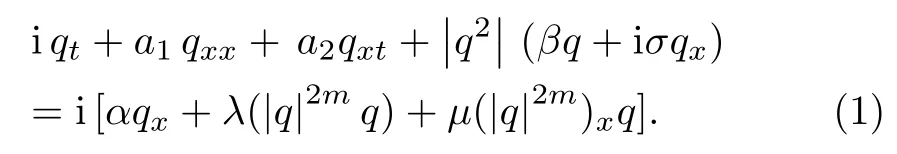
The first term of (1) represents temporal evolution of the pulses, where the two independent variablesxandtin the complex-valued functionq(x,t) represent the spatial and temporal components respectively.The parameter in the left hand side are classified asβis self-phase modulation, whileμis due to nonlinear dispersion, whilea1,a2are the group velocity dispersion and the spatio-temporal dispersions respectively.On the right hand sideγis the effect of inter-modal dispersion that is in addition to chromatic dispersion andρis the self-deepening effect while the coefficientngives the effect of nonlinear dispersion with full nonlinearity.Finally the parameternis the full nonlinearity parameter.
There are a variety of mathematical procedures that make the study of soliton dynamics possible.[1?5]These methods are very powerful and can help to find optical soliton solutions of the FLE.They can also help to present conservation laws to the model.
There are three principal axes to get the exact solutions to nonlinear partial differential equations(NLPDEs)namely the reduction methods, Lie symmetry group,and the ansatze approaches.The famous ansatze approaches are (G’/G)-expansion method,[6]extended Jacobian elliptic function expansion method,[7?8]the modified decomposition method,[9]the Riccati-Bernoulli Sub-ODE method,[10?11]the modified extended tanhfunction method,[12?13]the modified simple equation method,[14?15]the exp(?φ(ζ))-method,[16?17]the modified exp(?φ(ζ))-expansion method,[18]new extended direct algebraic method[19?20]and so on.One of these methods which is a powerful mathematical tool to obtaining the exact solutions for the nonlinear physical problems is the the Riccati-Bernoulli Sub-ODE method.
In Ref.[21], such an expansion idea was also presented.However, it is important to mention that there are recent studies showing the remarkable richness of solutions of partial differential equations.[22]To illustrate that, the authors found abundant exact interaction solutions, including lump-soliton, lump-kink, and lumpperiodic solutions.[23?25]
2 Optical Soliton Solutions for Perturbed Fokas-Lenells Equation (FLE)
This section is composed on the Riccati-Bernoulli Sub-ODE method[10?11]which is new technique (does not depend on the balance rule)arising to get the exact solution in terms of some parameters.If these parameters take definite values the solitary wave solution is obtained (Using good values of these parameters,we can obtain several solitary wave solutions).
2.1 Description of the Method
Consider the following nonlinear evolution equation

we use the wave transformation,
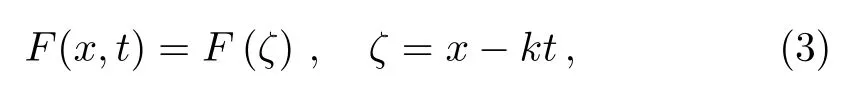
andkis constant.In order to reduce Eq.(2) to the following ODE
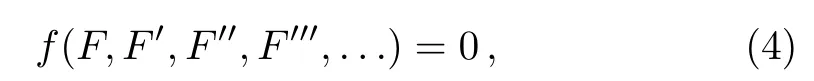
wherefis in general a polynomial function of its arguments,the subscripts denote the partial derivatives,whereF′=dF/dζ.
The Riccati-Bernoulli Sub-OD method consists of these steps
Step 1Suppose the solution of Eq.(4) according to the Riccati-Bernoulli Sub-ODE method as
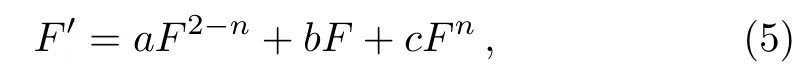
wherea,b,c, andnare constants to be determined later.The equation (5) is basis in the approach, is to use the Riccati-Bernoulli equation (5).However with dependent variablesFn?1, this equation could be transformed into a Riccati equation, whose general solutions are pretend by Eqs.(40)–(41) in Ref.[26].
Step 2From Eq.(5) and by directly calculating, we get
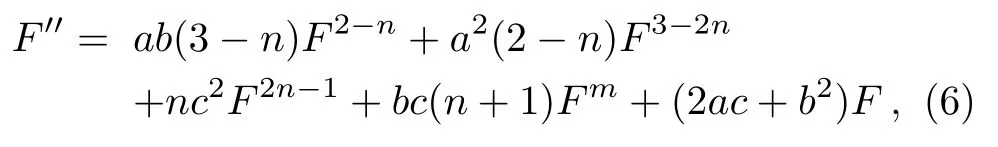
RemarkWhenac0 andn=0, Eq.(5) is a Riccati equation.This equation has be the subject of many investigations.For example, the authors of Ref.[26], analyze the possibilities of solutions which correspond to two Riccati equations.Whena≠0,c=0 andn≠1, Eq.(5) is a Bernoulli equation.Obviously, the Riccati equation and Bernoulli equation are special cases of Eq.(5).
Equation (5) has the following solutions:
Case 1Whenn=1, the solution of Eq.(5) is

Case 2Whenn≠1, b=0 andb2?4ac>0,andc=0,the solution of Eq.(5) is
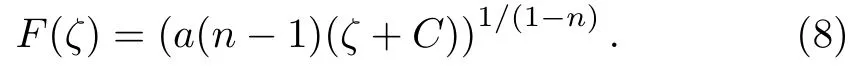
Case 3Whenn≠ 1, b≠ 0 andc=0, the solution of Eq.(5) is

Case 4Whenn≠1, a≠0 andb2?4ac<0,the solution of Eq.(5) is
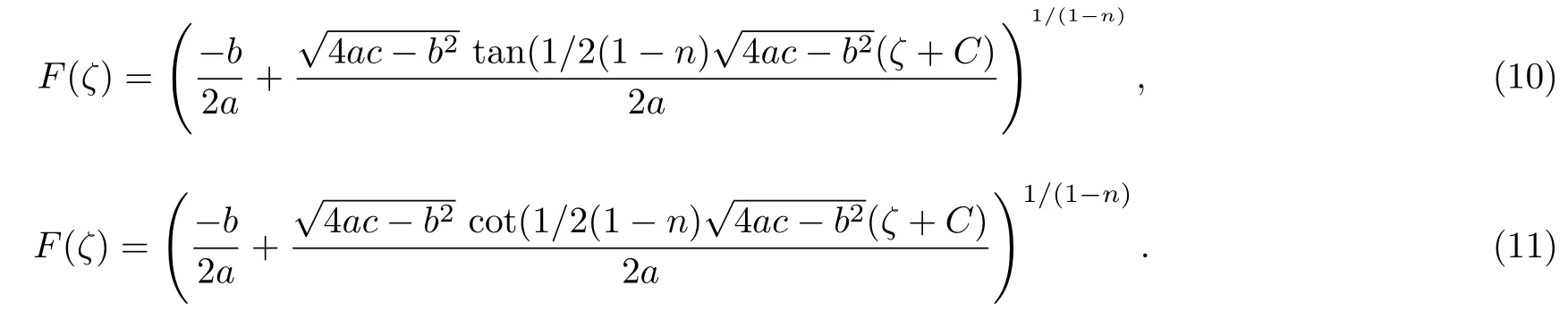
Case 5Whenn≠1, a≠0, andb2?4ac>0,the solution of Eq.(5) is
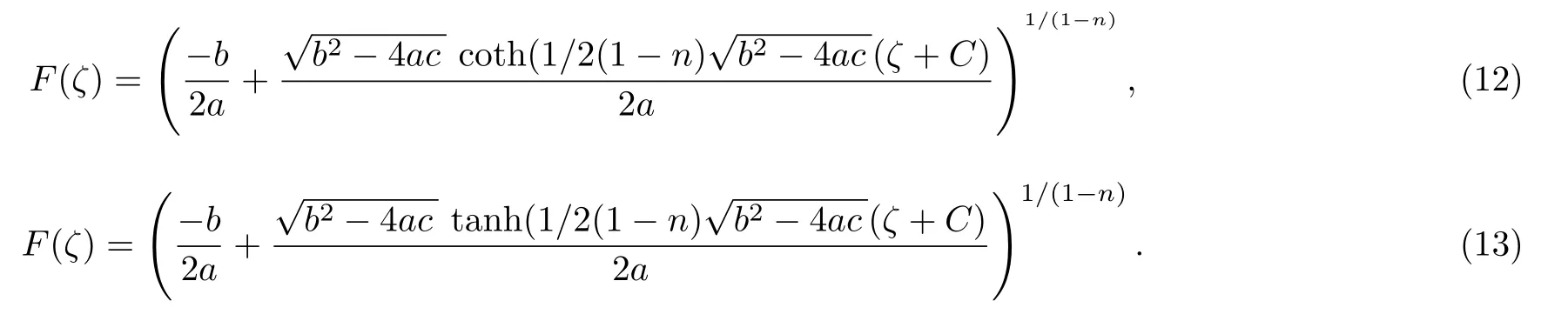
Case 6Whenn≠1, a≠0, andb2?4ac=0, the solution of Eq.(5) is
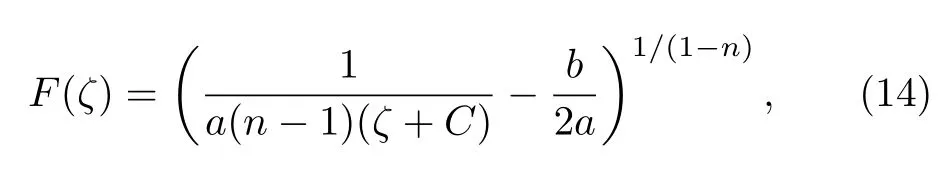
whereCis an arbitrary constant.
Step 3Substituting the derivatives ofuinto Eq.(5)yields an algebraic equation ofu.Noticing the symmetry of the right-hand item of Eq.(5) and setting the highest power exponents ofuto be equivalence in Eq.(5),mcan be determined.Comparing the coefficients ofuiyields a set of algebraic equations fora,b,candC.Solving the set of algebraic equations and substitutingm, a,b,c,C,ζ=μ(x+y ?2kt) to Eqs.(7)–(14), we can get the traveling wave solutions of Eq.(2).
3 Application
First of all, we introduce the following wave transformation
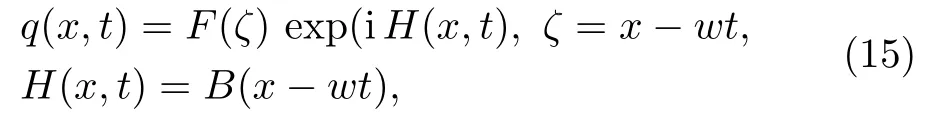
where these restrictionsσ=3λ ?2μ, α=?w+2a1B ?2wa2B,will represent the shape features of the wave pulse,andH(x,t) is the phase element of the soliton.
Moreover form=1, and by putting Eq.(15) into Eq.(1), we get the following ordinary differential equation
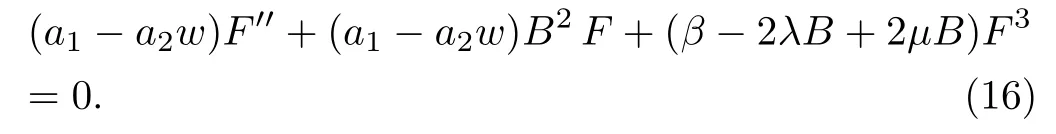
According to Riccati-Bernolli Sub-ODE method, we substitute aboutF′′, at Eq.(16) and by a suitable choose for the value ofn, then equating the coefficients of different power ofFto zero we get this system of algebraic equations,
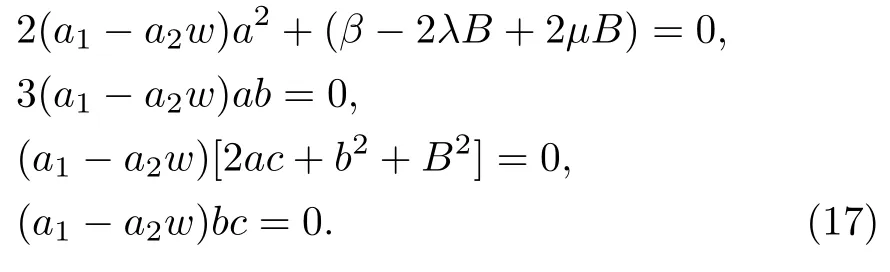
By solving this system of algebraic equations, we get
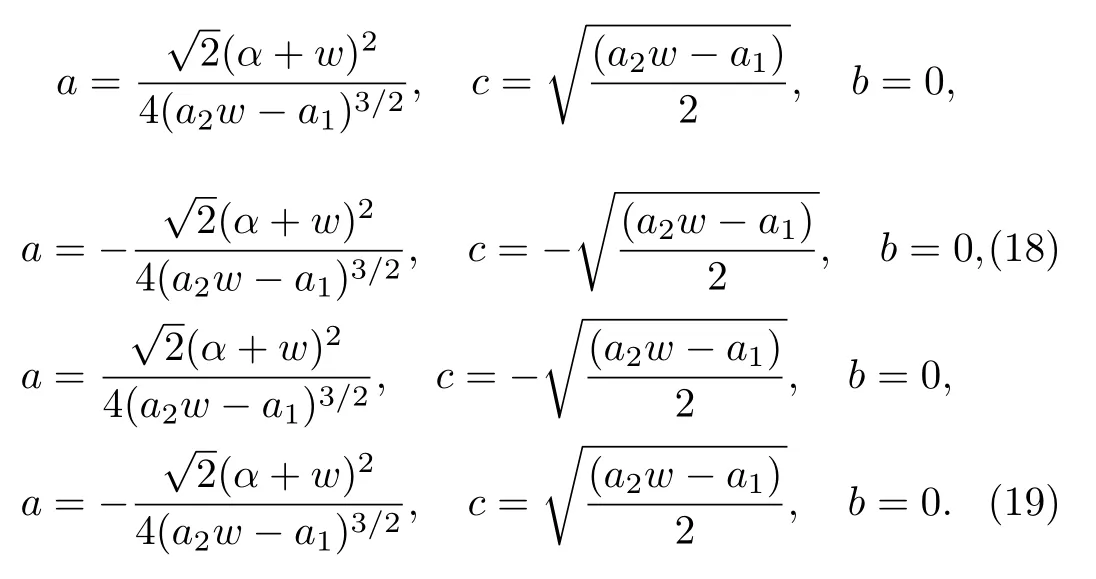
According to these obtained solutions and the constructed method we have the following cases
Case 1
(i) Whenn≠1, a≠0, andb2?4ac<0,
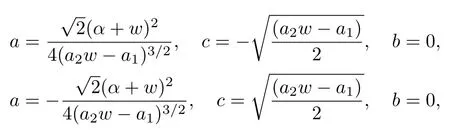
and the solution is
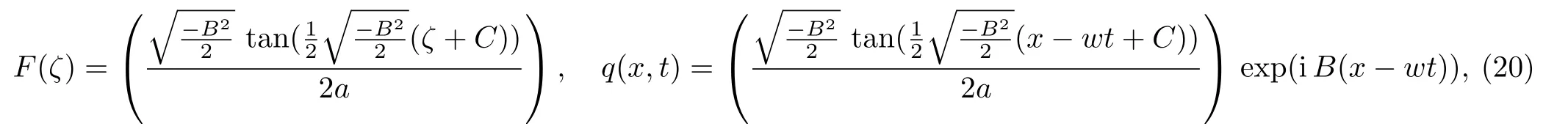
or
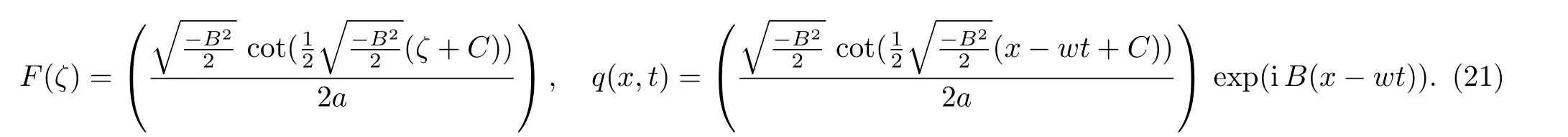
Case 2whenn≠1, a≠0, andb2?4ac>0,
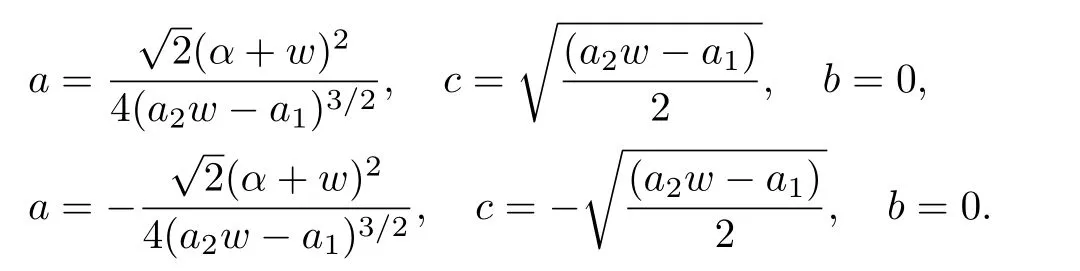
the solution is
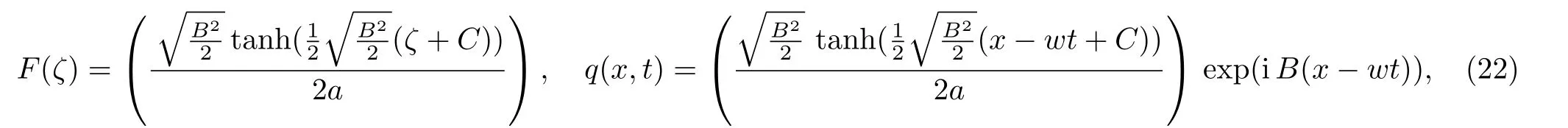
or
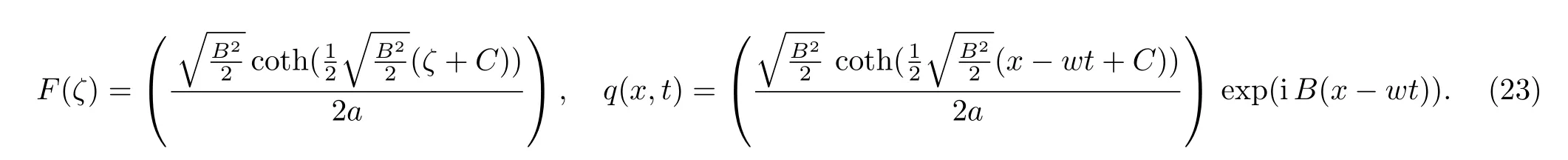
4 Results and Discussion
The main objective of this part is to give some graphical representations of the solutions found concerning the FLE.For that, the following values are used:w=2.0,a1=0.1,a2=0.5,andB=0.3.In the case of Figs.1–4,the constantCis equal to 0.9 while in the case of Fig.5,this constant has the value 9.0.These figures are plotted in 2D and 3D.
The curves obtained are the amplitudes of the solutions and are solitary waves, particularly kink and antikink soliton solutions.These figures help to have a good idea on the dynamics of the perturbed Fokas-Lenells equation used in several domains such as the electronic communications Internet blogs, facebook communication as well as twitter comments.Thus, we notice that the FLE has a great importance in the nonlinear research.One of these interests also comes from the fact that the FLE contains rich physical features in solitary wave’s theory and optical fibers phenomena.It is also important to mention that the outcomes of this work are new results not reported in the literature.

Fig.1 (Color online) Graphical representation of solution (20).
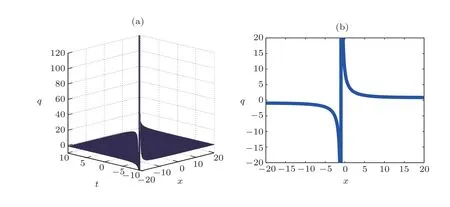
Fig.2 (Color online) Graphical representation of solution (21).
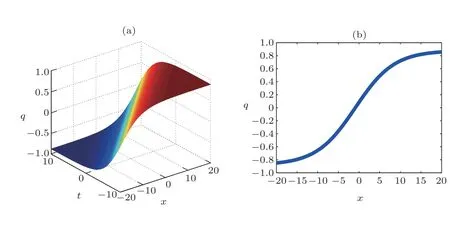
Fig.3 (Color online) Graphical representation of solution (22).
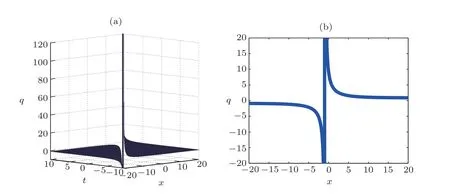
Fig.4 (Color online) Graphical representation of solution (23) for C=0.9..
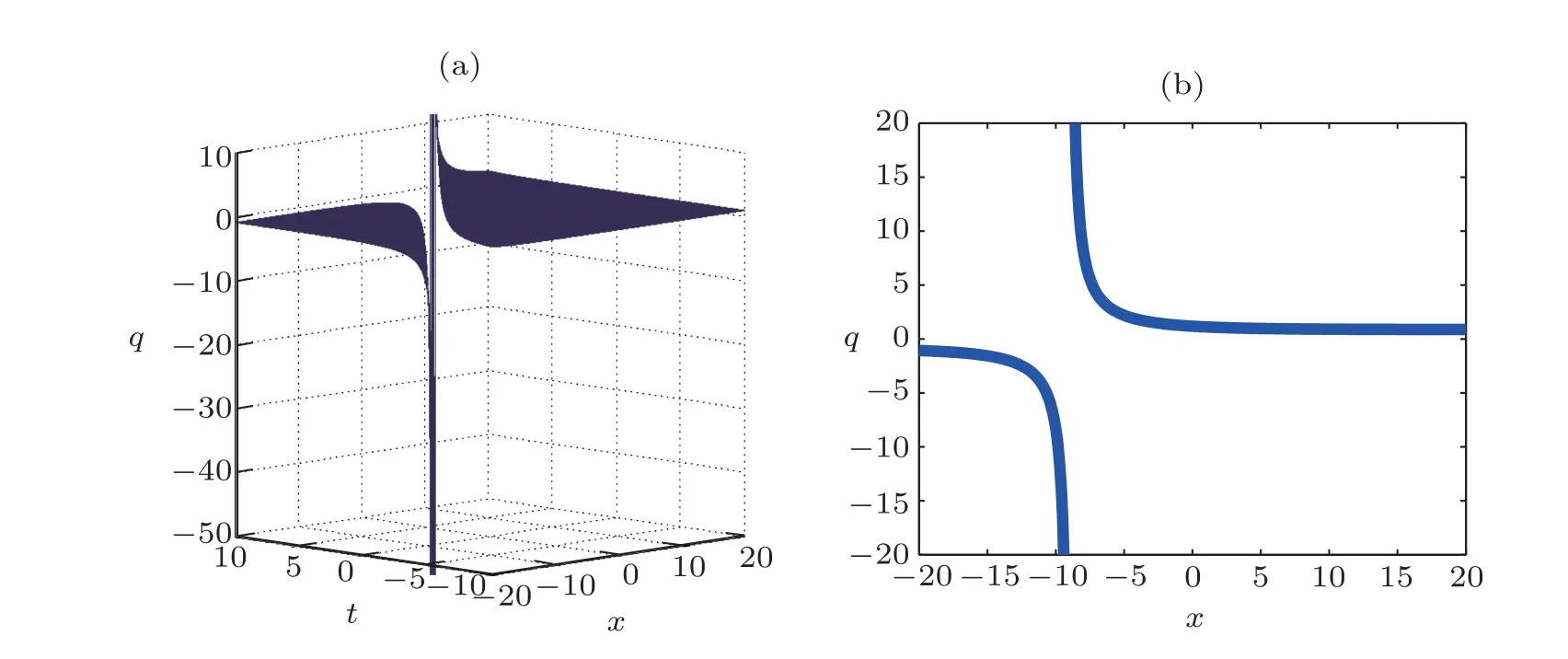
Fig.5 (Color online) Graphical representation of solution (23) for C=9.0.
5 Conclusions
In this work, using the solution of the auxiliary equation (5) in the Riccati-Bernoulli Sub-ODE method, we have found some new exact solutions which are positives forward future studies for the perturbed Fokas-Lenells equation (FLE).Also the perturbation terms will be included to demonstrate the phenomena of soliton cooling, obtain quasi-monochromatic solitons, and establish quasi-particle theory to suppress intra-channel collision of optical solitons and several other features.In addition,stochastic perturbation terms will be included to analyze the corresponding Langevin equations in order to obtain mean free velocity of the soliton.We also conclude that this technique is a concise, effective, powerful, direct, and convenient method and can be applied to other nonlinear PDEs.
 Communications in Theoretical Physics2019年11期
Communications in Theoretical Physics2019年11期
- Communications in Theoretical Physics的其它文章
- Numerical Study on the Whole Process of Fireball Evolution in Strong Explosion?
- Neural-Network Quantum State of Transverse-Field Ising Model?
- Magnetocaloric Effect in Anisotropic Mixed Spin–1 System:Pair Approximation Method
- Structure, Electronic, and Mechanical Properties of Three Fully Hydrogenation h-BN:Theoretical Investigations?
- Similar Early Growth of Out-of-time-ordered Correlators in Quantum Chaotic and Integrable Ising Chains?
- Fractional Angular Momentum of an Atom on a Noncommutative Plane?
