三角形內(nèi)心(內(nèi)切圓)在橢圓中的應(yīng)用舉隅
2020-03-02 06:51:40蘇藝偉
數(shù)理化解題研究 2020年4期
蘇藝偉
(福建省龍海第一中學(xué)新校區(qū) 363100)
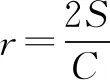
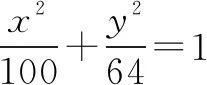
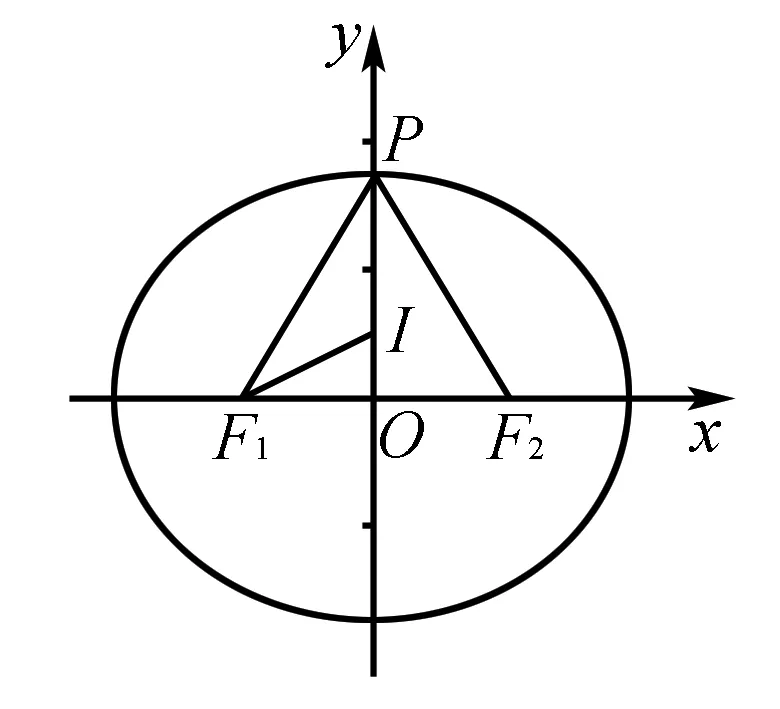
圖1
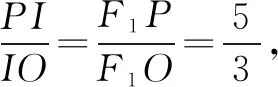
評(píng)析由于點(diǎn)P是橢圓上的一點(diǎn),所以取特殊情況,取點(diǎn)P為短軸端點(diǎn),結(jié)合三角形內(nèi)角平分線定理迅速求解.
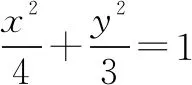
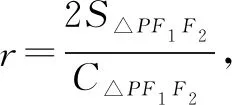
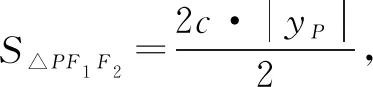
評(píng)析借助內(nèi)切圓半徑公式,結(jié)合橢圓性質(zhì)求解,很快得到答案.

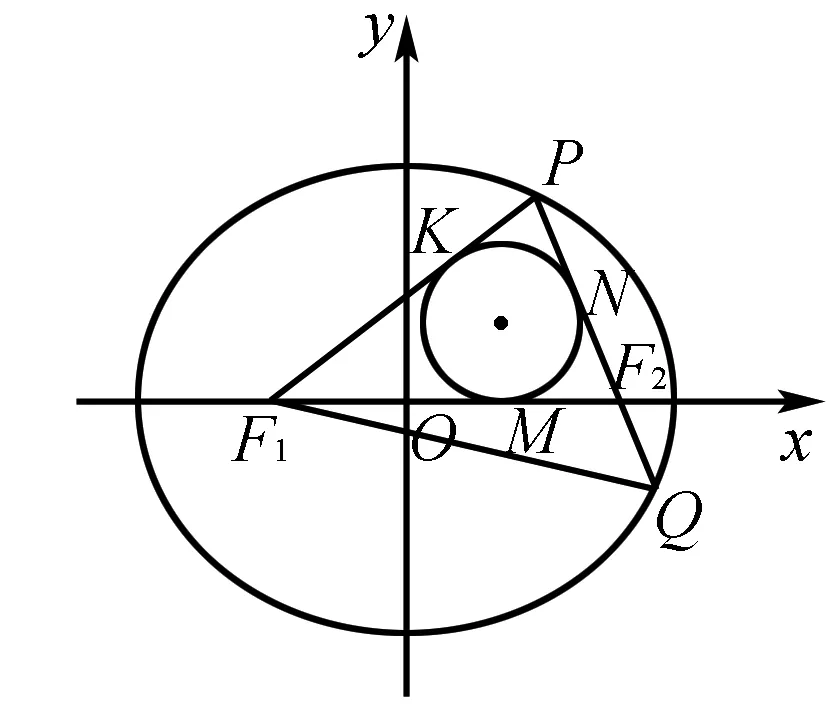
圖2
解析如圖2所示,設(shè)△F1PF2的內(nèi)切圓與該三角形的三邊分別相切于點(diǎn)M,N,K.不妨設(shè)F1M=F1K=x,F2M=F2N=z,PK=PN=y.
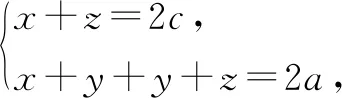
評(píng)析借助內(nèi)切圓與三角形的幾何性質(zhì),結(jié)合題目條件r+c=a,得到PF1⊥PQ,這是解決本道試題的關(guān)鍵.


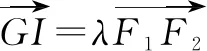
評(píng)析本題涉及到重心與內(nèi)心,準(zhǔn)確地掌握好重心和內(nèi)心的相關(guān)性質(zhì)是解決本道試題的關(guān)鍵.
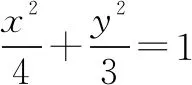
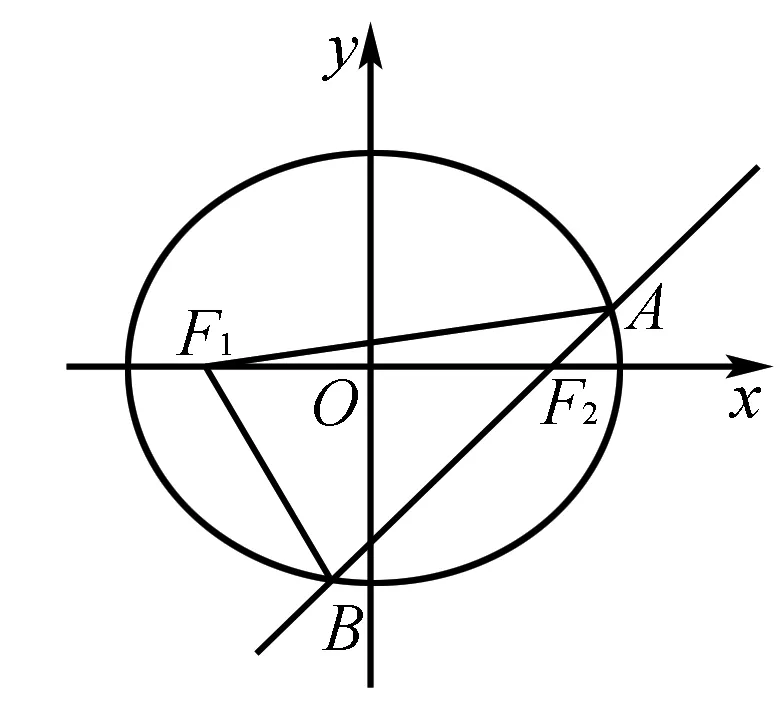
圖3
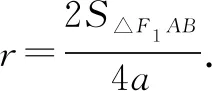
評(píng)析借助內(nèi)切圓半徑公式,聯(lián)立直線和橢圓方程求解.

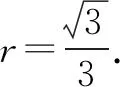
評(píng)析借助內(nèi)切圓半徑公式,結(jié)合橢圓中的等量關(guān)系求解.

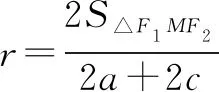
評(píng)析根據(jù)題目條件得到I是△F1MF2的內(nèi)心,結(jié)合內(nèi)切圓半徑公式求出離心率的取值范圍.
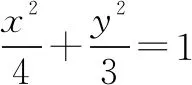
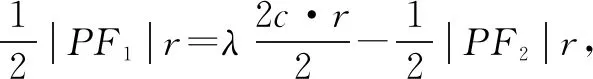

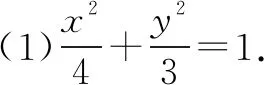
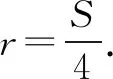
設(shè)直線l方程為x=my+1,
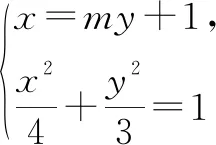
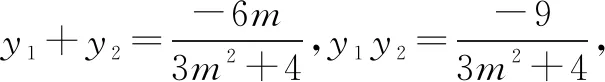
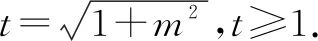
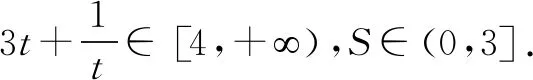
猜你喜歡
數(shù)學(xué)雜志(2022年5期)2022-12-02 08:32:10
音樂(lè)教育與創(chuàng)作(2022年6期)2022-10-11 01:14:20
中學(xué)生數(shù)理化(高中版.高考數(shù)學(xué))(2021年11期)2021-12-21 05:34:28
中等數(shù)學(xué)(2021年2期)2021-07-22 06:21:52
中學(xué)生數(shù)理化(高中版.高二數(shù)學(xué))(2021年12期)2021-04-26 07:43:38
中等數(shù)學(xué)(2020年9期)2020-11-26 08:07:28
中學(xué)數(shù)學(xué)雜志(2019年1期)2019-04-03 00:35:42
中等數(shù)學(xué)(2018年7期)2018-11-10 03:29:04
消費(fèi)導(dǎo)刊(2017年24期)2018-01-31 01:28:30
中學(xué)數(shù)學(xué)雜志(高中版)(2018年1期)2018-01-27 18:49:49

