偏序Menger PSM-空間中的耦合重合點定理

胡品,谷峰

(杭州師范大學理學院,浙江 杭州311121)

1.引言

1942年,Menger[1]用分布函數代替非負實數作為度量值,提出了Menger概率度量空間(簡稱Menger PM-空間)的概念.1960年,Schweizer與Sklar[2?3]在Menger PM-空間中引進t-范數,并討論了該空間的一些性質.1994年,張石生等[4]對Menger PM-空間的一些重要性質進行了總結.2006年,Mustafa和Sims[5]提出了G-度量空間的概念,它是度量空間的一個推廣.在此之后,Sedghi,RAO和Shobe[6]研究了由Dhage[7]提出的D-度量空間,同時引入了D?-度量空間的概念.2012年,Sedghi和Aliouche[8]提出了S-度量空間的概念,它是G-度量空間與D?-度量空間的一個推廣.

2014年,ZHOU等[9]在G-度量空間和Menger PM-空間的基礎上,引入了Menger概率G-度量空間(簡稱為MengerPGM-空間)的概念,并證明了幾個不動點定理.之后,ZHU等[10?11]在MengerPGM-空間中引入了?-壓縮條件和映象對弱相容的概念,建立了若干公共不動點定理.2015年,Hasanvand和Khanehgir[12]提出了Menger概率b-度量空間(簡稱為MengerPbM-空間)的概念,并討論了該空間中的不動點問題.

受上述研究工作的啟發(fā),本文提出一類新的概率度量空間―Menger PSM-空間,討論了該空間的拓撲性質,證明了偏序Menger PSM-空間中新的耦合重合點定理,并給出了一個用以說明新結果有效性的實際例子.

2.預備知識

定義2.8設(X,S?,?)是一個Menger PSM-空間,{xn}是X中的序列,x ∈X.

引理2.3設(X,S?,?)是一個Menger PSM-空間,{xn}是X中的序列,則以下敘述等價:

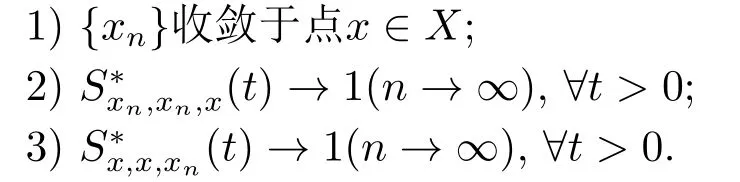
證1)?2).

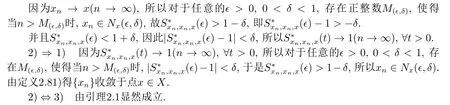
引理2.4設(X,S?,?)是一個具有連續(xù)t-范數?的Menger PSM-空間,則以下敘述等價:

1) 序列{xn}是柯西序列;

2) 對任意的? >0,0<δ <1,存在正整數M(?,δ),使得當n,m >M(?,δ)時,1?δ.

證 1)?2) 由定義2.8中2)直接可得.

定理2.2設(X,S?,?)是一個具有連續(xù)t-范數?的Menger PSM-空間,{xn},{yn}是X中的兩個序列,x,y ∈X.如果xn →x,yn →y(n →∞),則對于任意的t >0,.

證對于任意的t>0,存在δ >0,使得t>2δ,則

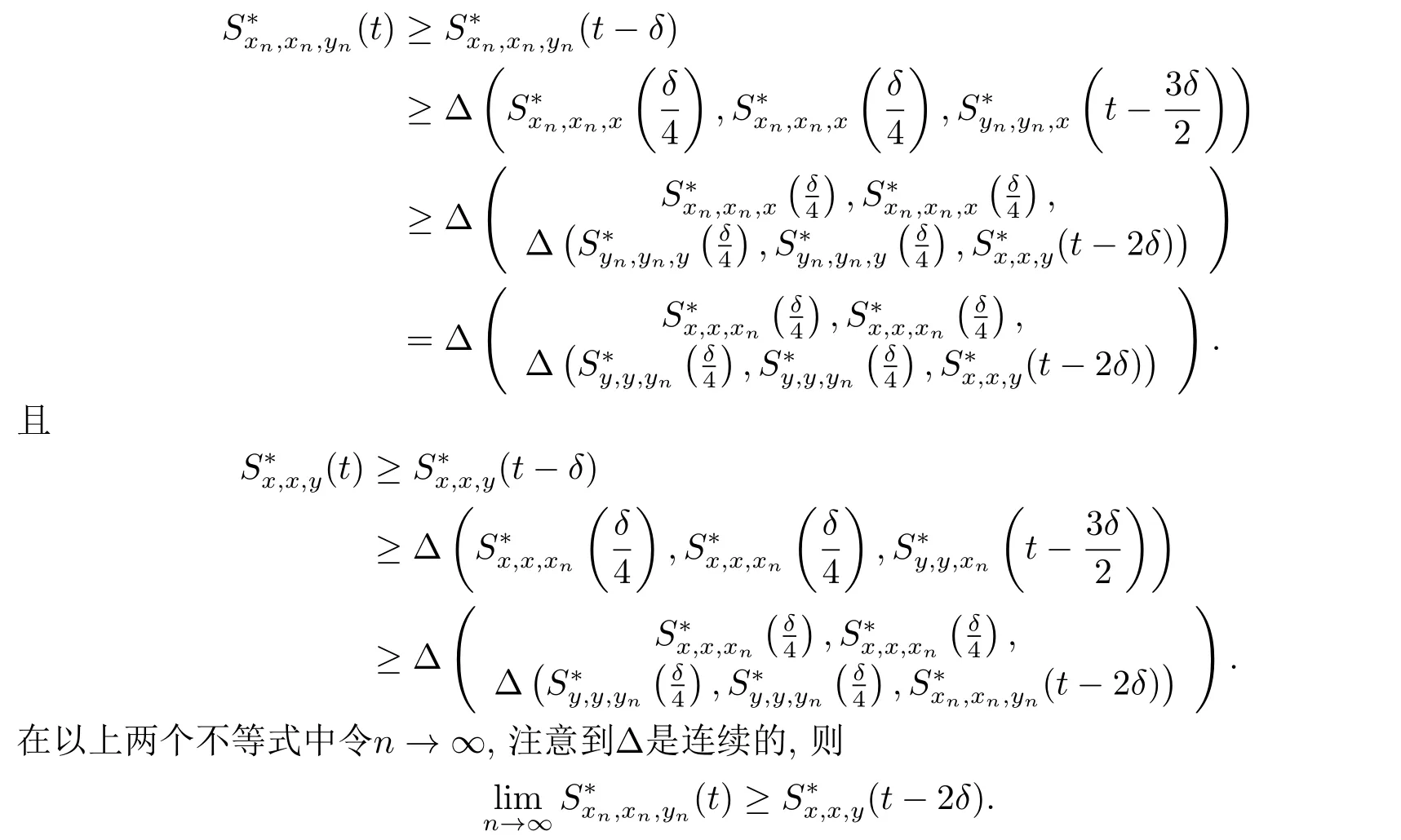
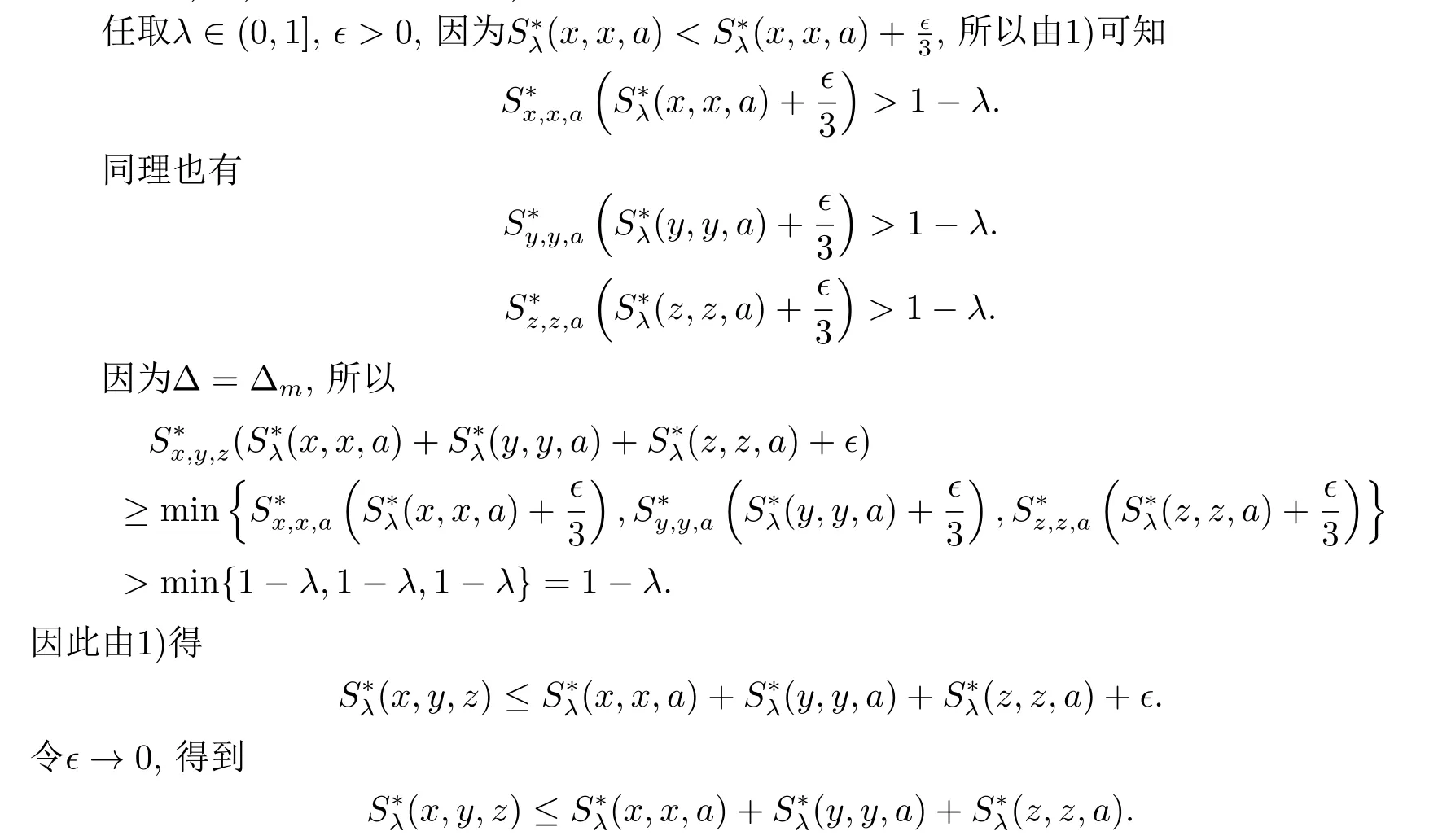
注2.1若映射g是恒等映射,則定義2.11和定義2.13等價.

定義2.14[15]一個元素(x,y)∈X×X被稱為是映射G:X×X →X和g:X →X的耦合重合點,如果G(x,y) =g(x),G(y,x) =g(y).稱(x,y)是G和g的耦合公共不動點,如果G(x,y)=g(x)=x,G(y,x)=g(y)=y.

定義2.15[15]設X是一個非空集合,G:X×X →X,g:X →X.映射G和g被稱為是可交換的,如果對于任意的x,y ∈X,g(G(x,y))=G(g(x),g(y)).

3.主要結果

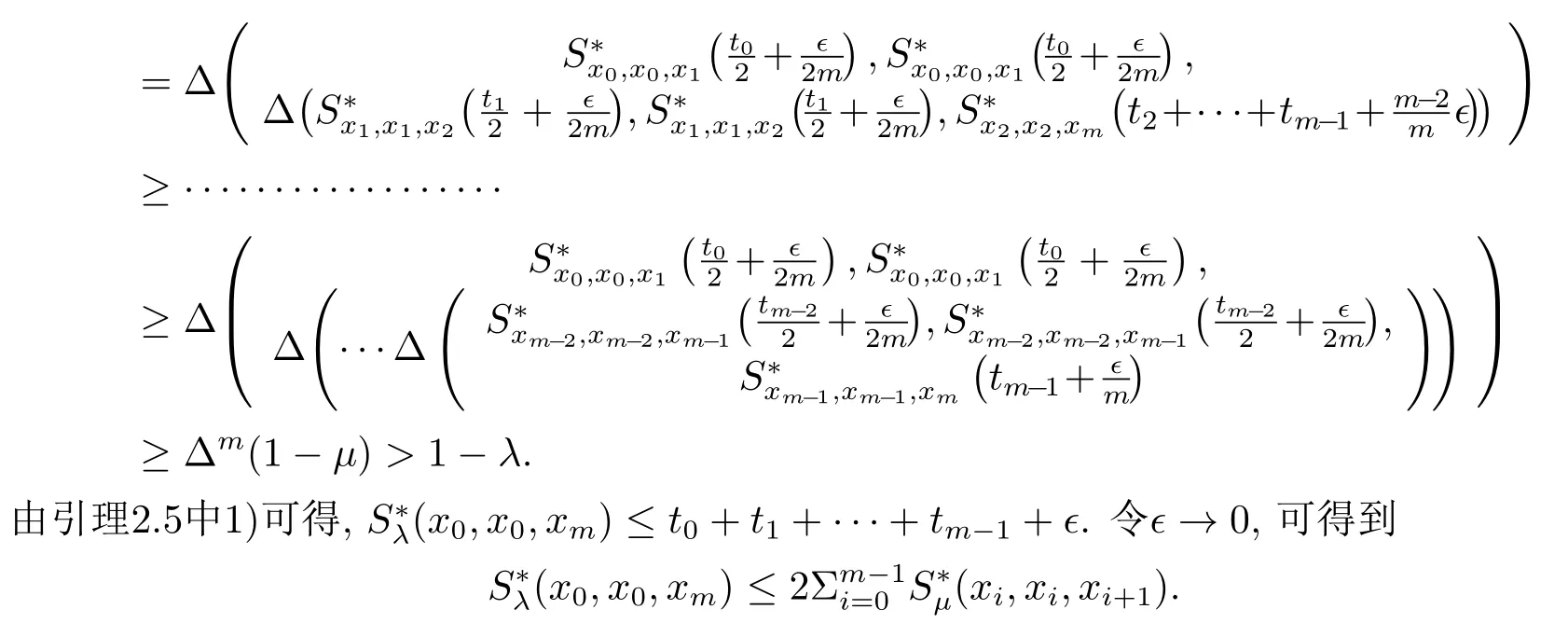
即

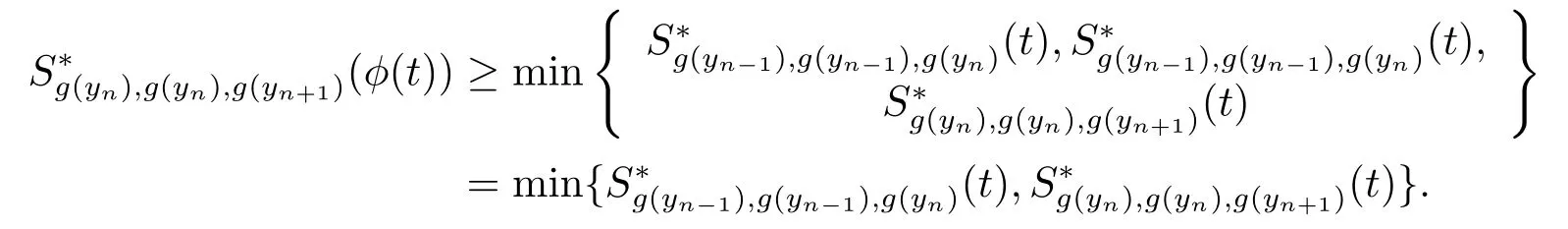
由引理3.2知{g(yn)}也是一個柯西序列.

因為X是完備的,所以存在x,y ∈X,使得

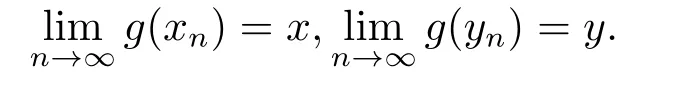
由g的連續(xù)性可得

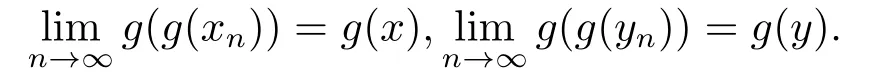
因為G和g是可交換的,所以

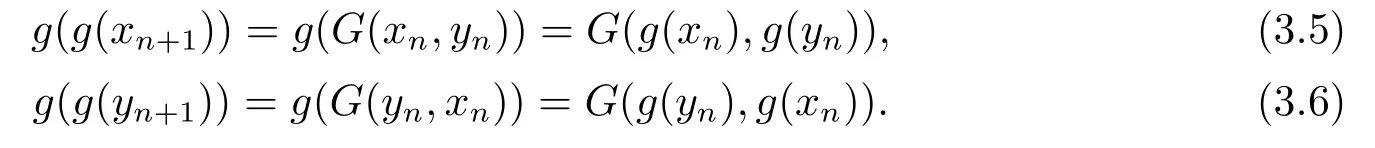
下證g(x)=G(x,y),g(y)=G(y,x).

假設條件(a)滿足,在式(3.5),(3.6)中令n →∞,由G的連續(xù)性可得

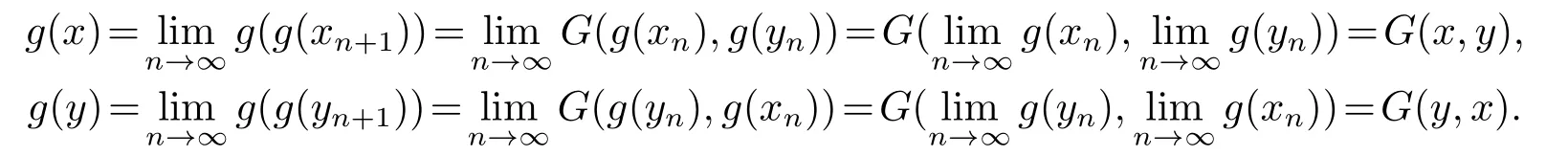
因此,g(x)=G(x,y),g(y)=G(y,x).

假設條件(b)滿足,因為{g(xn)}是不減的,{g(yn)}是不增的,并且當n →∞,g(xn)→x,g(yn)→y,所以由條件(b)可知g(xn)≤x,g(yn)≥y,?n ≥0.則由(PSM-2)和式(3.4)有

同理可得g(y)=G(y,x),因此(x,y)是映射G和g的耦合重合點.

下證討論耦合公共不動點的存在性和唯一性.注意到如果(X,≤)是一個偏序集合,則可在乘積X×X中定義以下偏序關系:

?(x,y),(u,v)∈X×X,(x,y)≤(u,v)?x ≤u,y ≥v.

定理3.2在定理3.1的條件下,如果對每一個(x,y),(x?,y?)∈X×X,都存在(u,v)∈X×X,滿足g(u)≤g(v)或者g(v)≤g(u),使得(G(u,v),G(v,u))∈X×X與(G(x,y),G(y,x))和(G(x?,y?),G(y?,x?))可比較,則G和g有唯一的耦合公共不動點,即存在唯一的(x,y)∈X×X,使得x=g(x)=G(x,y),y=g(y)=G(y,x).

證由定理3.1,耦合重合點構成的集合非空.下證如果(x,y),(x?,y?)是映射G和g的兩個耦合重合點,即g(x)=G(x,y),g(y)=G(y,x)和g(x?)=G(x?,y?)且g(y?)=G(y?,x?),則必有

g(x)=g(x?),g(y)=g(y?).

由假設存在(u,v)∈X×X,使得(G(u,v),G(v,u))∈X×X與(G(x,y),G(y,x))和(G(x?,y?),G(y?,x?))是可比較的,令u0=u,v0=v,則存在u1,v1∈X,使得g(u1)=G(u0,v0),g(v1)=G(v0,u0).類似于定理3.1的證明,可得到序列{g(un)},{g(vn)},滿足

g(un+1)=G(un,vn),g(vn+1)=G(vn,un).

同樣地,類似于定理3.1可證明{g(un)},{g(vn)}存在極限.

更進一步,令x0=x,y0=y,x?0=x?,y?0=y?,同樣地,可得到序列{g(xn)},{g(yn)},{g(x?n)},{g(y?n)}滿足

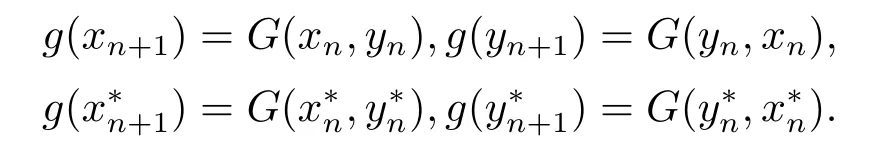
因為

(G(x,y),G(y,x))=(g(x1),g(y1))=(g(x),g(y))

和

(G(u,v),G(v,u))=(g(u1),g(v1))

是可比較的,不妨假設g(x)≤g(u1),g(y)≥g(v1)((g(x)≥g(u1),g(y)≤g(v1)的情況證明類似).容易得到(g(x),g(y))和(g(un),g(vn))是可比較的,即對任意的n ≥1,

g(x)≤g(un),g(y)≥g(vn).

由式(3.4),對于任意的n ≥1有

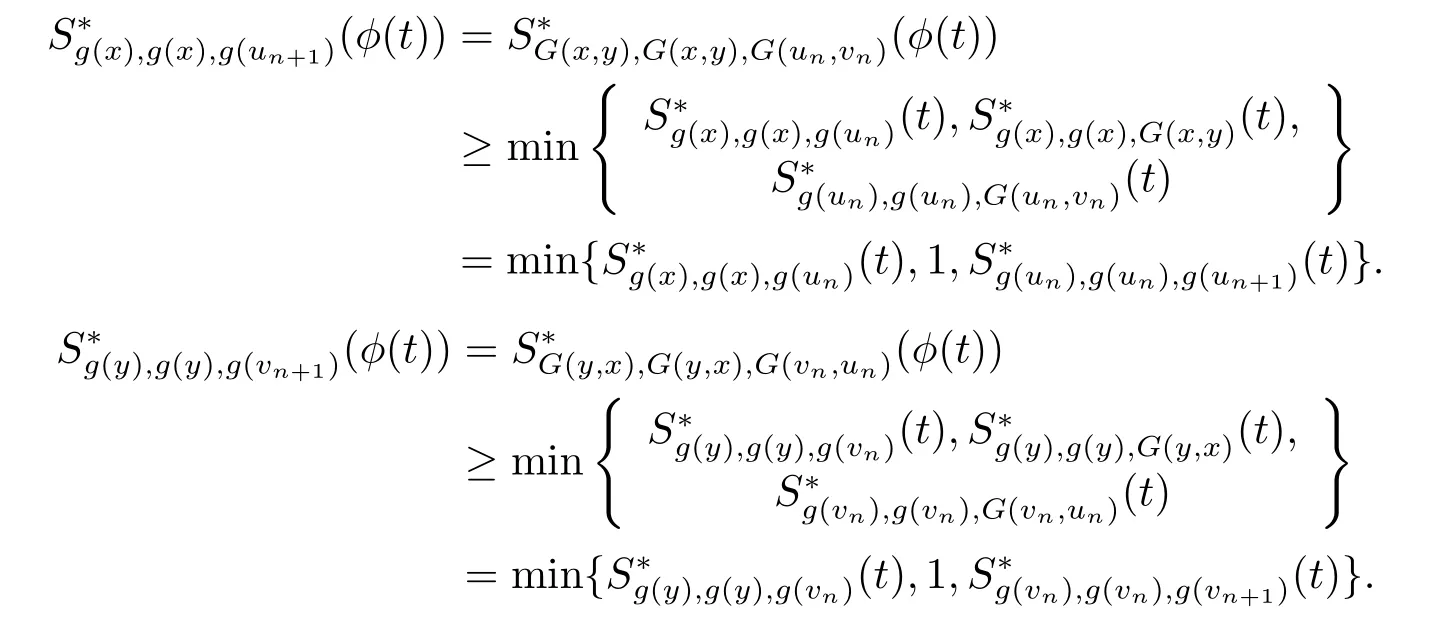
令n →∞,由定理2.2和引理2.6可得

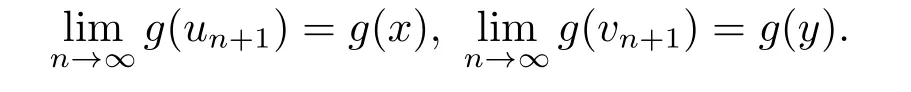
類似地,在定理3.2中令g=I或?(t)=kt,可得相應推論,限于篇幅省略.

4.應用

例4.1設X=[0,1],S(x,y,z)=|x?z|+|y?z|,min{a,b,c},?a,b,c ∈[0,1],則(X,S?,?)是一個完備的Menger PSM-空間.定義g:X →X和G:X×X →X如下: