測(cè)度微分方程的Lipschitz穩(wěn)定性

李寶麟,席 婭

(西北師范大學(xué)數(shù)學(xué)與統(tǒng)計(jì)學(xué)院,甘肅 蘭州 730070)

1 引言

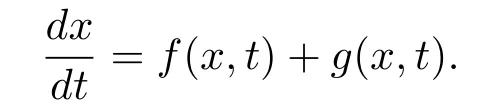
如果擾動(dòng)項(xiàng)g(x,t)是連續(xù)可積的,那么受擾動(dòng)之后的系統(tǒng)仍舊是常微分方程,它的解仍舊是連續(xù)的,如果擾動(dòng)項(xiàng)是脈沖型的,那么擾動(dòng)之后系統(tǒng)的狀態(tài)就不會(huì)隨著時(shí)間連續(xù)變化而變化,而是呈現(xiàn)出一種瞬時(shí)狀態(tài).為了研究這類(lèi)問(wèn)題,我們對(duì)上述方程加上一種脈沖型的擾動(dòng),這就給出如下形式的方程

其中Dx和Du分別表示函數(shù)x和u的分布導(dǎo)數(shù).形如(1.1)的方程叫做測(cè)度微分方程.由于測(cè)度微分方程的解沒(méi)有連續(xù)性,又沒(méi)有隨機(jī)系統(tǒng)那么復(fù)雜,因此,我們可以說(shuō)測(cè)度微分方程是一種不同于經(jīng)典不連續(xù)系統(tǒng)的新的不連續(xù)系統(tǒng).測(cè)度微分方程已經(jīng)被很多學(xué)者研究(見(jiàn)文獻(xiàn)[1–4]).

在文[5]中Dannan和Elaydi研究了常微分方程的Lipschitz穩(wěn)定性;文[6]中作者討論了一類(lèi)脈沖微分系統(tǒng)的Lipschitz穩(wěn)定性;文[7]中作者給出了脈沖泛函微分方程的Lipschitz穩(wěn)定性;文[8]中作者建立了廣義常微分方程的變差一致Lipschitz穩(wěn)定性,一致Lipschitz穩(wěn)定性和一致整體Lipschitz穩(wěn)定性,并通過(guò)滯后型脈沖微分方程在一定條件下與廣義常微分方程的等價(jià)關(guān)系,討論了滯后型脈沖微分方程的Lipschitz穩(wěn)定性.本文是在文[8]的基礎(chǔ)上,通過(guò)測(cè)度微分方程與廣義常微分方程的等價(jià)關(guān)系,定義了測(cè)度微分方程

和擾動(dòng)后的測(cè)度微分方程

的變差一致Lipschitz穩(wěn)定性,一致Lipschitz穩(wěn)定性和一致整體Lipschitz穩(wěn)定性,并建立了測(cè)度微分方程和擾動(dòng)后的測(cè)度微分方程的Lipschitz穩(wěn)定性定理.方程(1.2)和方程(1.3)的等價(jià)方程為

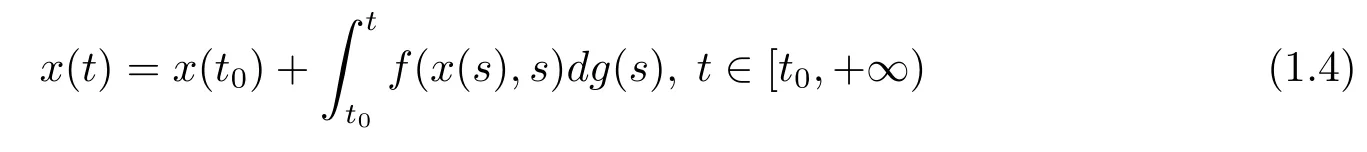
和

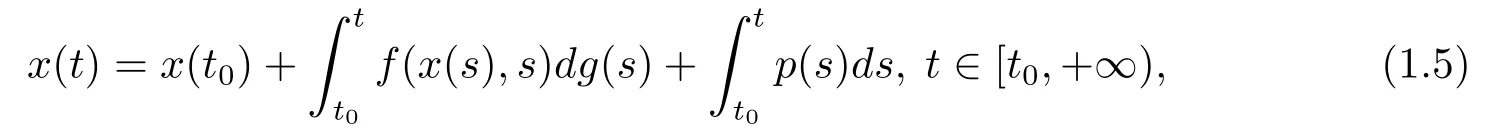
其中f:Bc×[t0,+∞)→Rn,Bc={y∈Rn,‖y‖＜c},g:[t0,+∞)→R,p:[t0,+∞)→Rn是比Lebesgue-Stieltjes可積更廣泛的Kurzweil-Henstock-Stieltjes可積函數(shù)和Kurzweil-Henstock可積函數(shù)(見(jiàn)文[10]).

函數(shù)x:[a,b]→Rn為[a,b]上的正則函數(shù)是指若函數(shù)x的左右極限

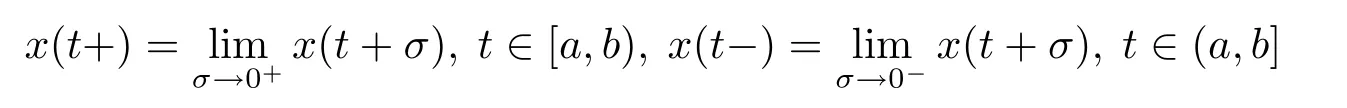
分別存在且有限(正則函數(shù)在有限區(qū)間上有界,在無(wú)窮區(qū)間上不一定有界).記G*([a,b],Rn),[a,b]?[t0,+∞)是定義在[a,b]上的正則函數(shù)全體,并且是左連續(xù)的.G*([t0,+∞),Rn)為關(guān)于函數(shù)x:[t0,+∞)→Rn的一個(gè)向量空間,使得對(duì)所有[a,b]?[t0,+∞),x|[a,b]屬于空間是關(guān)于所有x∈G*([t0,+∞),Rn)的一個(gè)向量空間,使得

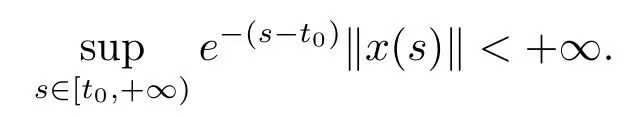
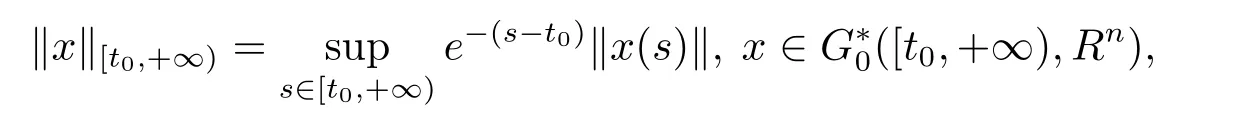
記Ω=Bc×[t0,+∞),本文假定函數(shù)f:Ω→Rn,g:[t0,+∞)→R,p:[t0,+∞)→Rn滿足下列條件

(H1)函數(shù)g:[t0,+∞)→R在[t0,+∞)上是不減的左連續(xù)函數(shù).

(H2)對(duì)每一個(gè)x∈G*([t0,+∞),Rn),s1,s2∈[t0,+∞),Kurzweil-Henstock-Stieltjes積分存在.

(H3)存在一個(gè)關(guān)于g的局部Kurzweil-Henstock-Stieltjes可積函數(shù)M:[t0,+∞)→R+,使得對(duì)任意的x∈G*([t0,+∞),Rn),s1,s2∈[t0,+∞),s1＜s2,

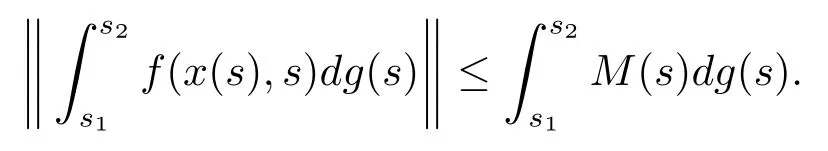
(H4)存在一個(gè)關(guān)于g的局部Kurzweil-Henstock-Stieltjes可積函數(shù)L:[t0,+∞)→R+,使得對(duì)任意的x,,s1,s2∈[t0,+∞),s1＜s2,

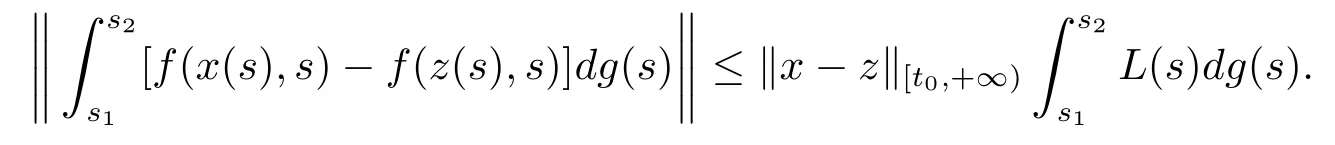
(H5)對(duì)每一個(gè)x∈G*([t0,+∞),Rn),s1,s2∈[t0,+∞),Kurzweil-Henstock積分存在.

(H6)存在一個(gè)局部Kurzweil-Henstock可積函數(shù)N:[t0,+∞)→R+,使得對(duì)任意的x∈G*([t0,+∞),Rn),s1,s2∈[t0,+∞),s1＜s2,

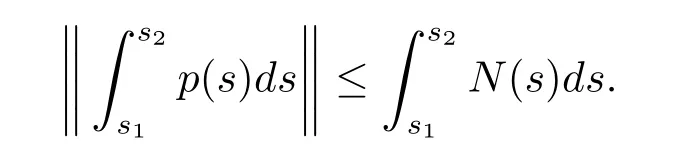
本文主要分為三個(gè)部分.第二部分給出了本文所需要的一些定義和引理,第三部分定義了測(cè)度微分方程和擾動(dòng)后的測(cè)度微分方程的變差一致Lipschitz穩(wěn)定性,一致Lipschitz穩(wěn)定性和一致整體Lipschitz穩(wěn)定性,并建立了測(cè)度微分方程和擾動(dòng)后的測(cè)度微分方程的Lipschitz穩(wěn)定性定理.

2 預(yù)備知識(shí)

本節(jié)介紹了廣義常微分方程的相關(guān)定義和引理及測(cè)度微分方程與廣義常微分方程的等價(jià)關(guān)系.

定義2.1[9]稱(chēng)函數(shù)U:[a,b]×[a,b]→Rn在區(qū)間[a,b]上Kurzweil可積,如果存在I∈Rn,使得對(duì)任意的ε＞0,存在正值函數(shù)δ:[a,b]→(0,+∞),使得對(duì)[a,b]上的任何δ(τ)-精細(xì)分劃D={(τj,[αj-1,αj]),j=1,2,···,k},其中τj∈[αj-1,αj]?[τj-δ(τj),τj+δ(τj)],有

稱(chēng)I為U在[a,b]上的Kurzweil積分,記作特別地,當(dāng)U(τ,t)=f(τ)g(t)時(shí),

定義2.2[9]設(shè)函數(shù)F:Ω→Rn,如果對(duì)所有的t∈[α,β],(x(t),t)∈Ω,且對(duì)任意的s1,s2∈[α,β],有等式成立,則稱(chēng)x:[α,β]→Rn是廣義常微分方程

在區(qū)間 [α,β]?[t0,+∞)上的解.

定義2.3[9]設(shè)不減函數(shù)h:[t0,+∞)→R,函數(shù)F:Ω→Rn屬于函數(shù)族F(Ω,h),是指F滿足以下條件:對(duì)任意的(x,s1),(x,s2)∈Ω,有

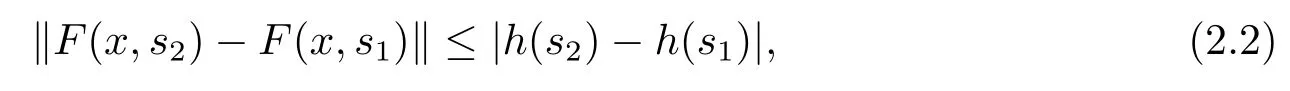
且對(duì)任意的(x,s1),(x,s2),(y,s1),(y,s2)∈Ω,有

引理 2.1[9]設(shè)F:Ω→Rn滿足(2.2)式,如果x:[α,β]→Rn,[α,β]?[t0,+∞)是方程(2.1)的一個(gè)解,則x在 [α,β]上有界變差,且并且在 [α,β]上x(chóng)與函數(shù)h具有相同的連續(xù)性,其中表示x在[α,β]上的全變差.

引理2.2[10]假設(shè)f:Ω→Rn滿足條件(H2),(H3),(H4),并且g:[t0,+∞)→R滿足條件(H1),對(duì)任意的τ0∈[t0,+∞),并且定義函數(shù)F:Ω→Rn為

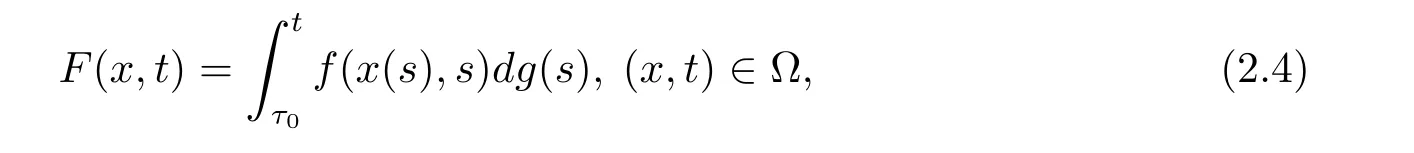
則F∈F(Ω,h),其中h:[t0,+∞)→R是不減的左連續(xù)函數(shù),且

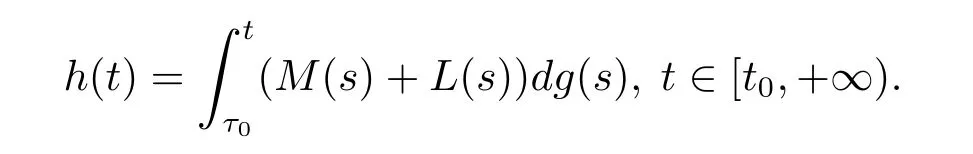
引理2.3[11]假設(shè)f:Ω→Rn滿足條件(H2),(H3),(H4),并且g:[t0,+∞)→R滿足條件(H1),且p:[t0,+∞)→Rn滿足條件(H5)和(H6),對(duì)任意的τ0∈[t0,+∞),并且定義函數(shù)G:Ω→Rn為

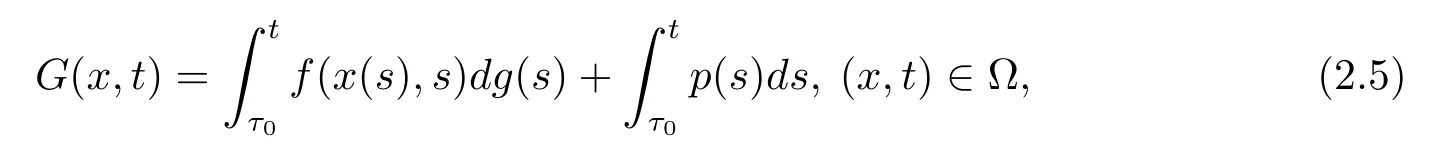
則G∈F(Ω,h),其中h:[t0,+∞)→R是不減的左連續(xù)函數(shù),且

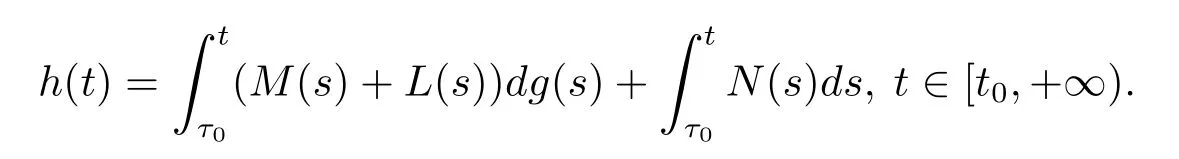
引理2.4[10]假設(shè)f:Ω→Rn滿足條件(H2),(H3),(H4),并且g:[t0,+∞)→R滿足條件(H1),如果函數(shù)x:[a,b]→Rn,[a,b]?[t0,+∞)是測(cè)度微分方程(1.2)的解,當(dāng)且僅當(dāng)x是廣義常微分方程

在[a,b]上的解,其中函數(shù)F由(2.4)式給定.

引理2.5[11]假設(shè)f:Ω→Rn滿足條件(H2),(H3),(H4),并且g:[t0,+∞)→R滿足條件(H1),且p:[t0,+∞)→Rn滿足條件(H5)和(H6),如果函數(shù)x:[a,b]→Rn,[a,b]?[t0,+∞)是測(cè)度微分方程(1.3)的解,當(dāng)且僅當(dāng)x是廣義常微分方程

在[a,b]上的解,其中函數(shù)G由(2.5)式給定.

引理 2.6[9]設(shè)F∈F(Ω,h),假設(shè)x:[α,β]→Rn,[α,β]?[t0,+∞)在 [α,β]上是有界變差函數(shù),使得對(duì)每一個(gè)s∈[α,β],(x(s),s)∈Ω,則積分存在.

引理2.7[9]設(shè)F∈F(Ω,h),假設(shè)V:[t0,+∞)×Rn→R+是使得對(duì)任意的y∈Rn,函數(shù)V(·,y):[t0,+∞)→R+在(t0,+∞)上是左連續(xù)的,假設(shè)以下條件成立

(i)對(duì)任意的(t,x),(t,y)∈[t0,+∞)×Rn,常數(shù)L＞0,有|V(t,x)-V(t,y)|≤L‖x-y‖.

(ii)存在一個(gè)實(shí)函數(shù)Φ:Rn→R,使得對(duì)于廣義常微分方程(2.6)在區(qū)間(a,b)?[t0,+∞)上的每一個(gè)解y:(a,b)→Rn,對(duì)于t∈(a,b),有

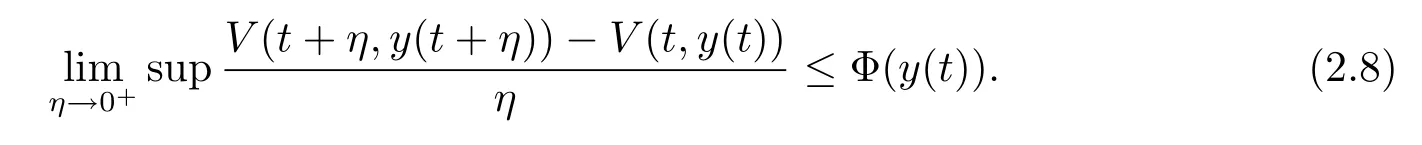
若:[α,β]→Rn,t0≤α＜β＜+∞是區(qū)間 [α,β]上的有界變差函數(shù),并且在 (α,β]上是左連續(xù)的,則不等式

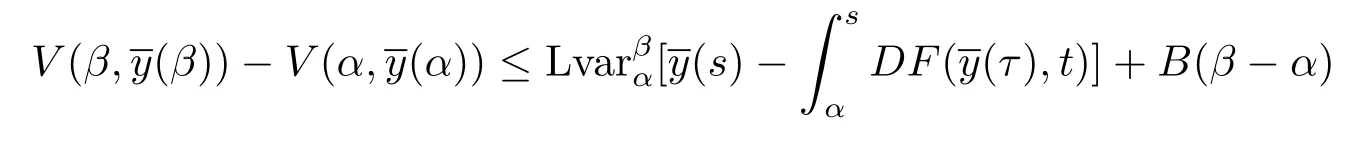
引理2.8[9]設(shè)G∈F(Ω,h),假設(shè)V:[t0,+∞)×Rn→R+是使得對(duì)任意的y∈Rn,函數(shù)V(·,y):[t0,+∞)→R+在(t0,+∞)上是左連續(xù)的,假設(shè)以下條件成立:

(i)對(duì)任意的(t,x),(t,y)∈[t0,+∞)×Rn,常數(shù)L＞0,有|V(t,x)-V(t,y)|≤L‖x-y‖.

(ii)存在一個(gè)實(shí)函數(shù)Φ:Rn→R,使得對(duì)于廣義常微分方程(2.7)在區(qū)間(a,b)?[t0,+∞)上的每一個(gè)解y:(a,b)→Rn,對(duì)于t∈(a,b),有

若:[α,β]→Rn,t0≤α＜β＜+∞是區(qū)間 [α,β]上的有界變差函數(shù),并且在 (α,β]上是左連續(xù)的,則不等式

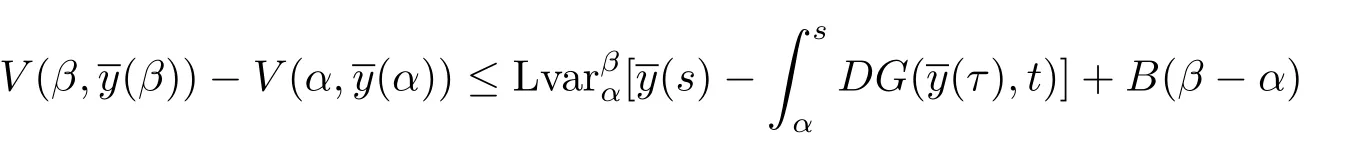
3 主要結(jié)果

本節(jié)定義了測(cè)度微分方程(1.2)及擾動(dòng)后的測(cè)度微分方程(1.3)的變差一致Lipschitz穩(wěn)定性,一致Lipschitz穩(wěn)定性和一致整體Lipschitz穩(wěn)定性.利用廣義常微分方程的Lipschitz穩(wěn)定性結(jié)果給出了測(cè)度微分方程的變差一致Lipschitz穩(wěn)定性,一致整體Lipschitz穩(wěn)定性定理及其證明.

定義3.1測(cè)度微分方程(1.2)的平凡解x≡0是變差一致Lipschitz穩(wěn)定的,若存在A＞0,以及δ＞0,使得若:[α,β]→Bc,t0≤α＜β＜+∞是 [α,β]上的有界變差函數(shù),并且在(α,β]上左連續(xù),當(dāng)(α)‖＜δ和

時(shí),則有

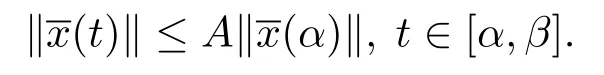
定義3.2測(cè)度微分方程(1.2)的平凡解x≡0是

(i)一致Lipschitz穩(wěn)定的,若存在A＞0,δ＞0,使得若:[α,β]→Bc,t0≤α＜β＜+∞是測(cè)度微分方程(1.2)在[α,β]上的一個(gè)解,當(dāng)(α)‖＜δ時(shí),則(t)‖ ≤(α)‖,t∈[α,β].

(ii)一致整體Lipschitz穩(wěn)定的,若存在A＞0,使得若:[α,β]→Bc,t0≤α＜β＜+∞是測(cè)度微分方程(1.2)在[α,β]上的一個(gè)解,則(t)‖ ≤(α)‖,t∈[α,β].

注若測(cè)度微分方程(1.2)的平凡解x≡0是變差一致Lipschitz穩(wěn)定的,則它是一致Lipschitz穩(wěn)定的.

定義3.3測(cè)度微分方程(1.3)的平凡解x≡0是變差一致Lipschitz穩(wěn)定的,若存在A＞0,以及δ＞0,使得若:[α,β]→Bc,t0≤α＜β＜+∞是 [α,β]上的有界變差函數(shù),并且在(α,β]上左連續(xù),當(dāng)(α)‖＜δ和

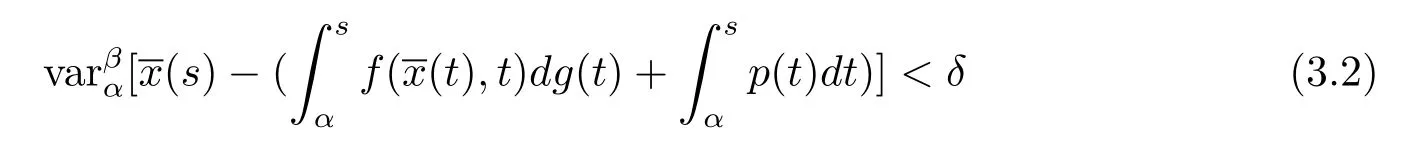
時(shí),則有

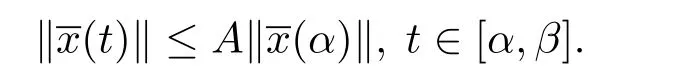
定義3.4測(cè)度微分方程(1.3)的平凡解x≡0是

(i)一致Lipschitz穩(wěn)定的,若存在A＞0,δ＞0,使得若:[α,β]→Bc,t0≤α＜β＜+∞是測(cè)度微分方程(1.3)在[α,β]上的一個(gè)解,當(dāng)(α)‖＜δ時(shí),則

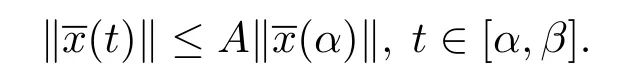
(ii)一致整體Lipschitz穩(wěn)定的,若存在A＞0,使得若:[α,β]→Bc,t0≤α＜β＜+∞是測(cè)度微分方程(1.3)在[α,β]上的一個(gè)解,則

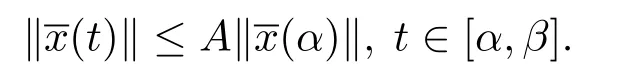
注若測(cè)度微分方程(1.3)的平凡解x≡0是變差一致Lipschitz穩(wěn)定的,則它是一致Lipschitz穩(wěn)定的.

定理3.1設(shè),其中假設(shè)V滿足以下條件

(i)對(duì)所有的t∈[t0,+∞),有V(t,0)=0.

(iii)存在一個(gè)常數(shù)K＞0,使得

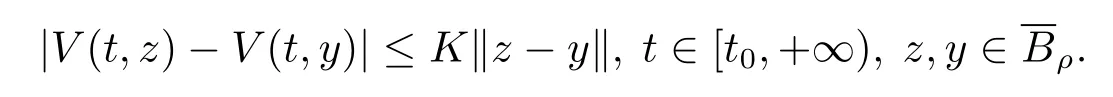
(iv)存在一個(gè)單調(diào)遞增函數(shù)b:[0,+∞)→[0,+∞)滿足b(0)=0,使得對(duì)所有的t∈[t0,+∞),有V(t,x)≥b(‖x‖).

則方程(1.2)的平凡解x≡0是變差一致Lipschitz穩(wěn)定的.

證根據(jù)引理2.2,需驗(yàn)證F∈F(Ω,h),F由(2.4)式給定,Ω=Bc×[t0,+∞).因?yàn)閒:Ω→Rn滿足條件(H2),(H3),(H4),并且g:[t0,+∞)→R滿足條件(H1),使得對(duì)任意的(x,s2),(x,s1)∈Ω,有

且對(duì)任意的(x,s2),(x,s1),(z,s2),(z,s1)∈Ω,由條件(H4),有

所以F∈F(Ω,h),其中τ∈[t,+∞),且h:[t,+∞)→R是000不減的左連續(xù)函數(shù).

由引理2.4可知,測(cè)度微分方程(1.2)的解也是廣義常微分方程(2.6)的解,因此它們的解都是有界變差函數(shù).

以下證明測(cè)度微分方程(1.2)的平凡解x≡0是變差一致Lipschitz穩(wěn)定的.

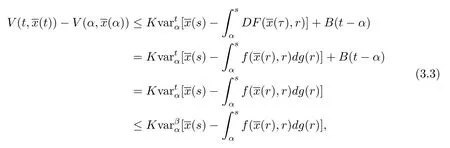
因?yàn)棣怠?,所以且由條件(i)和(iii),有即

對(duì)于ε＞0,使得不等式成立.設(shè)δ＞0,使得 2Kδ＜b(ε).若

因此由(3.3)和(3.4)式,有

由于2Kδ＜b(ε),則有

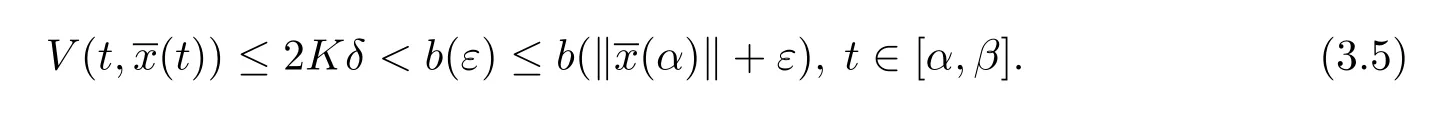
另外,由條件(iv),有

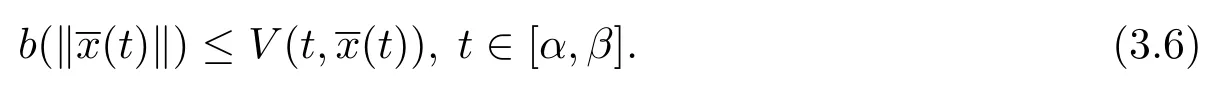
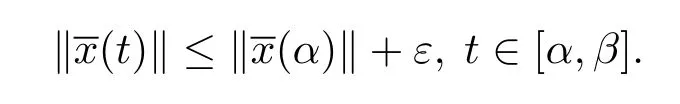
由定義3.1,取A=1,并且由ε的任意性,則滿足,則測(cè)度微分方程(1.2)的平凡解x≡0是變差一致Lipschitz穩(wěn)定的.

定理3.2設(shè)滿足定理3.1中的條件(i),(ii),(iii)和(v),并且滿足條件

(iv′)對(duì)所有的,有V(t,x)≥‖x‖.

則方程(1.2)的平凡解x≡0是一致整體Lipschitz穩(wěn)定的.

證設(shè)是測(cè)度微分方程 (1.2)在 [α,β]上的解.由條件(iii),(v)及引理2.4和引理2.7,其中Φ≡0,所以對(duì)任意的t∈[α,β],有

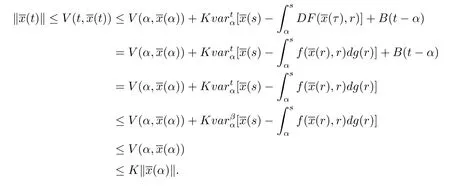
定理3.3設(shè),其中假設(shè)V滿足以下條件

(i)對(duì)所有的t∈[t0,+∞),有V(t,0)=0.

(iii)存在一個(gè)常數(shù)K＞0,使得

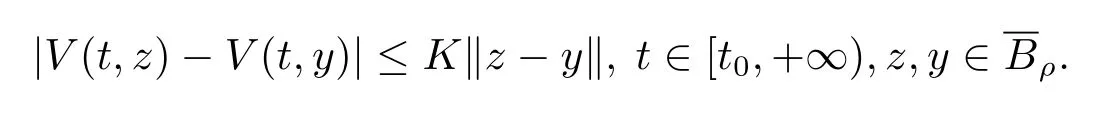
(iv)存在一個(gè)單調(diào)遞增函數(shù)b:[0,+∞)→[0,+∞)滿足b(0)=0,使得對(duì)所有的t∈[t0,+∞),有V(t,x)≥b(‖x‖).

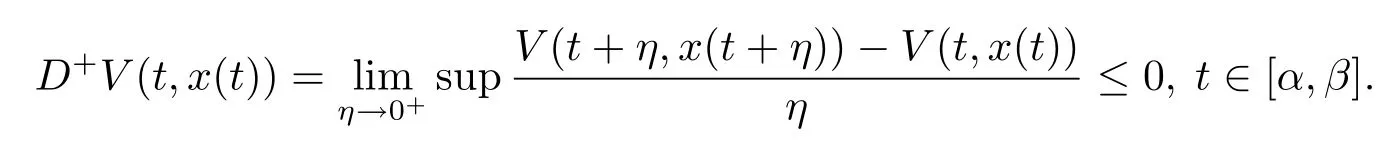
則方程(1.3)的平凡解x≡0是變差一致Lipschitz穩(wěn)定的.

證根據(jù)引理2.3,需驗(yàn)證G∈F(Ω,h),G由(2.5)式給定,Ω=Bc×[t0,+∞).因?yàn)閒:Ω→Rn滿足條件(H2),(H3),(H4),并且g:[t0,+∞)→R滿足條件(H1),p:[t0,+∞)→Rn滿足條件(H5)和(H6),使得對(duì)任意的(x,s2),(x,s1)∈Ω,有

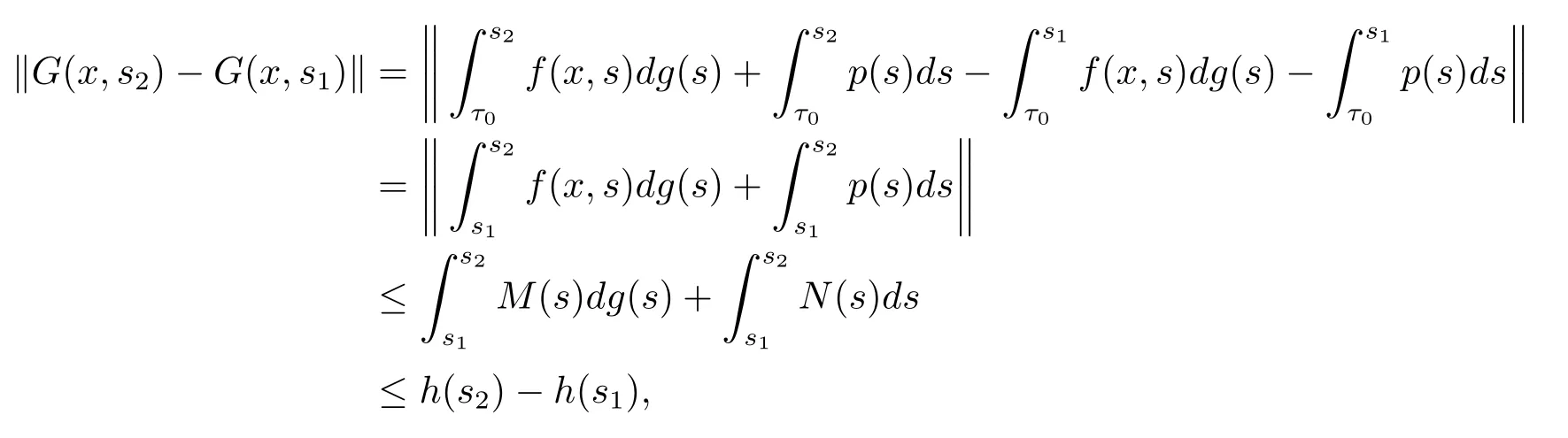
且對(duì)任意的(x,s2),(x,s1),(z,s2),(z,s1)∈Ω,由條件(H4),有

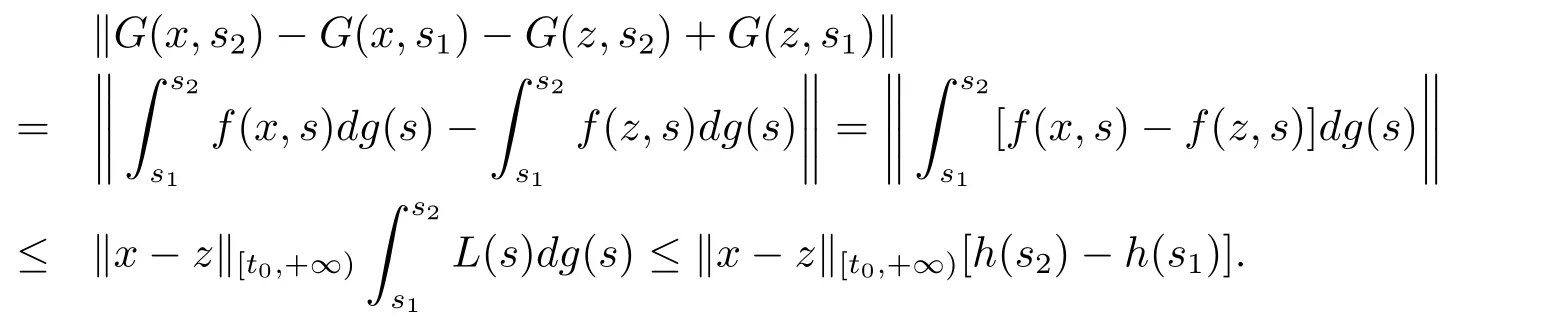
所以G∈F(Ω,h),其中τ0∈[t0,+∞),且h:[t0,+∞)→R是不減的左連續(xù)函數(shù).

由引理2.5可知,測(cè)度微分方程(1.3)的解也是廣義常微分方程(2.7)的解,因此它們的解都是有界變差函數(shù).

以下證明測(cè)度微分方程(1.3)的平凡解x≡0是變差一致Lipschitz穩(wěn)定的.

因?yàn)棣怠?,所以且由條件(i)和(iii),有即

對(duì)于ε＞0,使得不等式成立.設(shè)δ＞0,使得 2Kδ＜b(ε).若

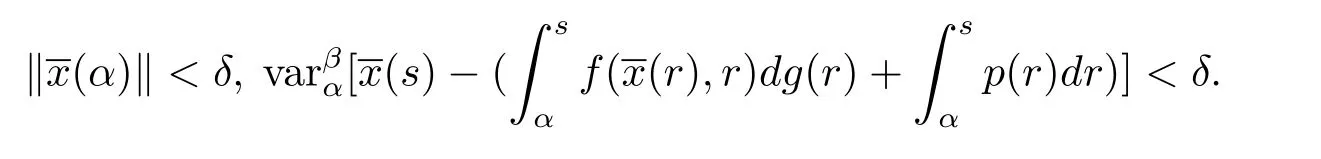
因此由(3.7)和(3.8)式,有

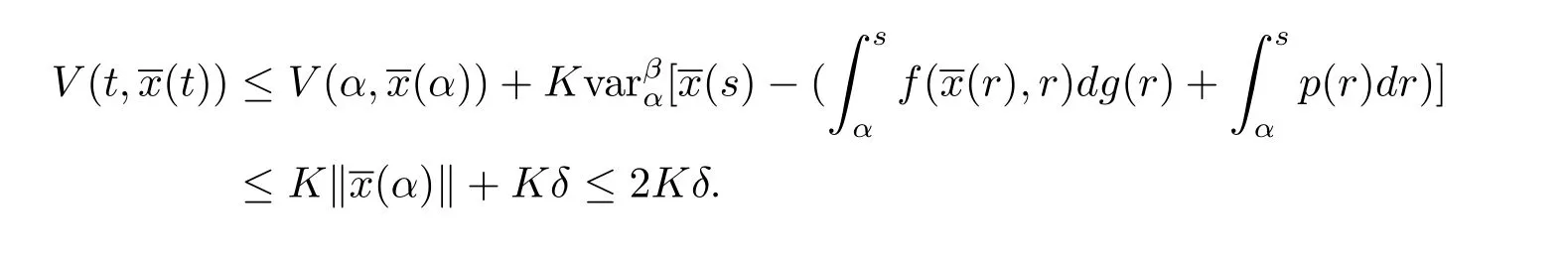
由于2Kδ＜b(ε),則有

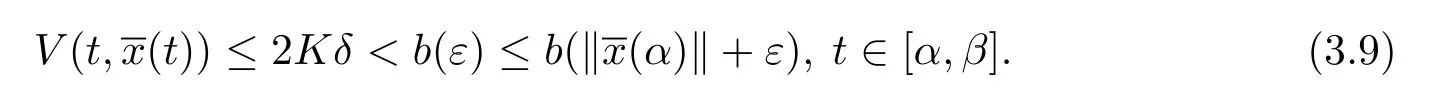
另外,由條件(iv),有

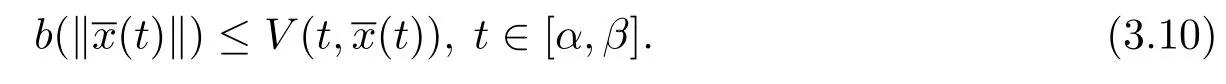
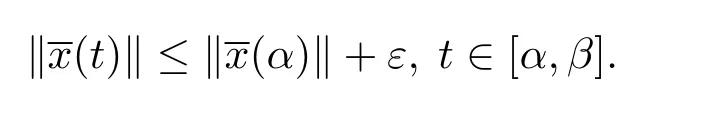
由定義3.3,取A=1,并且由ε的任意性,則滿足,則測(cè)度微分方程(1.3)的平凡解x≡0是變差一致Lipschitz穩(wěn)定的.

定理3.4設(shè)滿足定理3.3中的條件(i),(ii),(iii)和(v),并且滿足條件:

(iv′)對(duì)所有的有V(t,x)≥‖x‖.

則方程(1.3)的平凡解x≡0是一致整體Lipschitz穩(wěn)定的.

證設(shè)是測(cè)度微分方程 (1.3)在 [α,β]上的解.由條件(iii),(v)及引理2.5和引理2.8,其中Φ≡0,所以對(duì)任意的t∈[α,β],有