PARAMETRIC REPRESENTATIONS OF QUASICONFORMAL MAOOINGS*
Zhenlian LIN (林珍連)
School of Mathematical Sciences, Huaqiao University, Quanzhou 362021, China E-mail : zhenlian@hqu.edu.cn
Qingtian SHI (石擎天)
School of Mathematics and Computer Science, Quanzhou Normal University,Quanzhou 362000, China E-mail : shiqingtian2013@gmail.com



2 Two Counterexamples of the Parametric Representations


3 Parametric Representation of
Given a measurable functionμ(z),letfμbe the normal solution of the Beltrami equation?zf=μ?zf.Ifμhas compact support on?,thenfμcan be represented as follows:
Theorem 3.1([2])Letμ(z)be a measurable function which has compact support on??C.If‖μ‖∞≤k<1,then there exists a unique solutionf=fμsuch thatf(0)=0 andfz?1∈Lpforp>2.Moreover,fcan be expressed in the following form:




4 Auxiliary Application of Parametric Representation
Using the parametric representation ofin Theorem 1.1,Eremenko and Hamilton derive the formula(1.6)to prove the area distortion theorem[6].This method is relatively simple compared to others,and the sharp constants in the area distortion inequality are obtained from it,but we find that the parametric representation theorem is false and the area distortion formula(1.6)can not be derived from the equalities(1.3)–(1.5).In this section,by applying Theorem 3.4,we get that the formula(1.6)still holds true for allf∈;that is,the method used by Eremenko and Hamilton in[6]can still be used to prove the area distortion theorem.
In fact,because
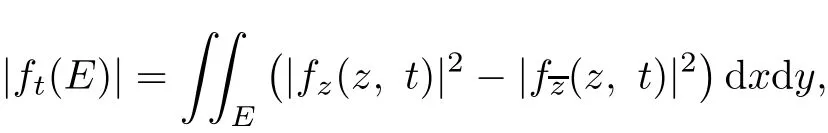
we have that
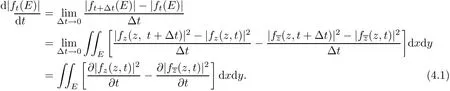
Astis a real variable,then,by applying the parametric representation in(3.3),

Therefore,from(4.2),the relation(4.1)can be simplified to
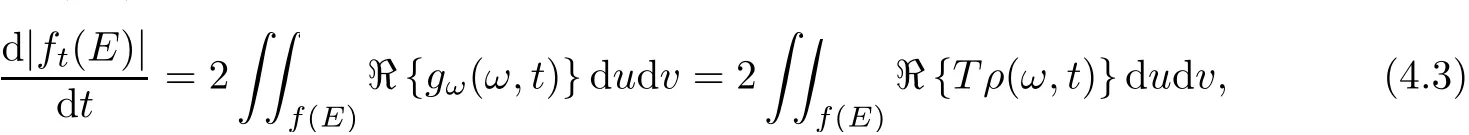
by the fact that(Pρ)ω=Tρ,which implies that the relation(1.6)holds true for the parametric representation in(3.3).
 Acta Mathematica Scientia(English Series)2020年6期
Acta Mathematica Scientia(English Series)2020年6期
- Acta Mathematica Scientia(English Series)的其它文章
- IT?O DIFFERENTIAL REPRESENTATION OF SINGULAR STOCHASTIC VOLTERRA INTEGRAL EQUATIONS?
- ON THE NUCLEARITY OF COMPLETELY 1-SUMMING MAPPING SPACES*
- EXISTENCE AND UNIQUENESS OF THE POSITIVE STEADY STATE SOLUTION FOR A LTKA-VTE PEDPY MD WIH CING*
- ASYMPTOTICS OF THE CROSS-VARIATION OF YOUNG INTEGRALS WITH RESPECT TO A GENERAL SELF-SIMILAR GAUSSIAN PROCESS?
- THE DECAY ESTIMATES FOR MAGNETOHYDRODYNAMIC EQUATIONS WITH COULOMB FORCE*
- VAR AND CTE BASED OPTIMAL REINSURANCE FROM A REINSURER'S PERSPECTIVE*
