Steady-state entanglement and heat current of two-qubit in two heat baths

WANG Meijiao,XIA Yunjie,LI Yingde,CAO Lianzhen,YANG Yang,ZHAO Jiaqiang*

(1 Shandong Provincial Key Laboratory of Multi-Photon Entanglement and Manipulation,Department of Physics and Optoelectronic Engineering,Weifang University,Weifang 261061,China;2 Shandong Provincial Key Laboratory of Laser Polarization and Information Technology,College of Physics and Engineering,Qufu Normal University,Qufu 273165,China)

Abstract:Non-equilibrium environment is one of the most common dissipative factors encountered in the application of quantum system.The dynamic evolution and steady-state solutions of two coupled qubits in both equilibrium and non-equilibrium environments are studied systematically.The results show that in the equilibrium bath,enhancing the coupling strength,increasing the energy detuning and raising the temperature of the heat bath are all beneficial to the enhancement of the entanglement.While in the nonequilibrium bath,the entanglement is enhanced(suppressed)with the increasing of the temperature gradient for the low(high)average temperature.In addition,the relationship between the heat current and the energy detuning,the coupling strength and the temperature of bath is also studied.It is found that for the two qubits in two independent heat baths or in two common heat baths,the influence of parameters on the evolution of the system and the heat current is different.By selecting appropriate coupling strength,energy detuning and temperature gradient,the stable heat current between two heat baths can be obtained,so the steady-state entanglement of the system.

Key words:quantum optics;steady-state entanglement;heat current;independent and common heat baths;equilibrium and non-equilibrium environment

0 Introduction

Non-equilibrium environment is one of the most common dissipative factors in quantum information processing(QIP)[1].With the development of quantum information,the dynamic evolution of open quantum system in the non-equilibrium environment has attracted more researchers’attention.One reason for the concern is that the interaction between open quantum system and external environment will inevitably lead to the transient attenuation of the entanglement.During the evolution process of the system,not only a single heat bath is contacted,but multiple heat baths are contacted[2-8].Different temperatures of the heat baths have different effects on the entanglement.The steady-state entanglement rather than instantaneous entanglement of the system is discussed.The steady-state entanglement can be generated by heat current between high and low temperature gradient of the non-equilibrium thermal baths[9-17].The second reason is that the coupling strengths between each subsystem and the coupling strength between the system and the thermal environment will affect the entanglement of the composite quantum system.The influence of coupling coefficient on the steady-state entanglement and heat current is discussed from the aspects of strong coupling and weak coupling[18,19].

Focusing on the above-mentioned situation,the premise is that the system is weakly coupled to the thermal environment in this paper,and the master equation is established by Born-Markov approximation.The steadystate solution of the equation is obtained under the eigenstate representation[20,21],so as to study the steady-state entanglement of the system in the presence of stable heat current,that is,when there is temperature gradient between high and low temperature heat baths.The two coupled qubits either interact with two independent heat baths(IHB)or interact with two common heat baths(CHB).The steady-state entanglement will be discussed in terms of equilibrium and non-equilibrium cases of two heat baths.And the effects of the energy detuning,the coupling strength and the temperature of bath are also studied.

1 Physical model

ThebasicmodelofthisresearchinFig.1isthattwocoupledqubitsA,Bareincontactwithhightemperature T1of heat bath a and low temperature T2of heat bath b,respectively.We specially analyze two cases:the IHB case and the CHB case.In the former case,the two qubits are immersed in two IHBs,for the latter case,the two qubits are immersed in two CHBs.According to the interaction between the system and the heat baths,the total Hamiltonian can be expressed as

where HSis the Hamiltonian of the system,HBrepresents the Hamiltonian of two heat baths,HIstands for the interaction Hamiltonian between the system and the heat baths.

The Hamiltonian HScan be written as(?=1)

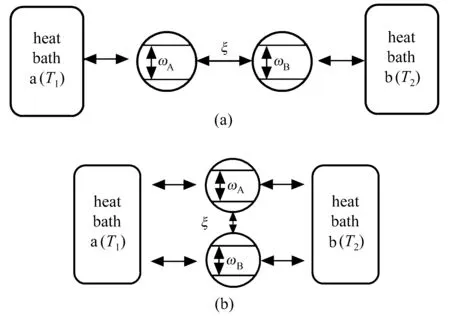
圖1 兩耦合量子比特A和B與兩個(gè)熱庫a和b相互作用的物理模型示意圖Fig.1 Schematic diagram of the physical model with the two coupled qubits A and B interacting with two heat baths a and b

2 The steady-state entanglement and heat current of the system interacting with two IHBs

In this section,we study the quantum thermalization of the two coupled qubits which are immersed in two IHBswithdifferenttemperature.Wedepicttheevolutionofthetwoqubitsintermsofaquantummasterequation.By solving the equations of the motion of the density matrix elements to obtain steady-state solution,we study the steady-state properties and the heat current of the two coupled qubits.

2.1 Equation of motion and steady-state solutions

Due to the system is weakly coupled to the thermal environment and Born-Markov approximation,the principal equation of the system is expressed as

2.2 Steady-state entanglement

The concurrence[23]is

Firstly,we consider the steady-state entanglement of two coupled qubits with T1=T2=T.The concurrence as the function of the temperature thermal baths T for various coupling strengths ξ and energy detunings Δω are plotted in Fig.2(a),Fig.2(b),respectively.Since the steady-state of the system is in the ground state|00〉with no correlation,the concurrence at T=0 is always zero.As the temperature increases,the steady-state entanglement increases and reaches it’s maximal value.Then,the entanglement decreases with a further increase inthetemperatureandeventuallyvanishes.Infact,thestateatthehightemperatureisclosetoacompletelymixed state,which contains no entanglement.Fig.2 shows that the more steady-state entanglement can be created and the larger region of T can sustain the entanglement for a stronger coupling ξ in(a)and a larger energy detuning Δω in(b).We also see the entanglement sudden death(ESD)when the bath temperature increases up to the critical value Tc.The dependences of Tcon the energy detunings Δω and coupling strengths ξ are shown in Fig.2(c).One can see that Tcincreases with Δω (ξ)for a given ξ(Δω )being consistent with the results in Fig.2(a),Fig.2(b).Therefore,one can enhance the steady-state entanglement in high temperature regimes by increasing the energy detuning and coupling strengths.

圖2 平衡熱庫T1=T2=T,(a)不同耦合強(qiáng)度ξ和(b)不同能量失諧Δω下,共生糾纏作為熱庫溫度T的函數(shù);(c)為不同耦合強(qiáng)度ξ下臨界溫度Tc作為能量失諧Δω的函數(shù).假設(shè)(a)Δω=2γ,(b)ξ=10γ,其他參數(shù)為= = = = γ,ωm=20γFig.2 In equilibrium baths with T1=T2=T,the concurrence is the function of the temperature of heat baths T for various coupling strengths ξ in(a)and energy detunings Δω in(b).The critical temperature Tcas a function of the energy detunings Δω for different ξ is shown in(c).Setting Δω =2γ in(a)and ξ=10γ in(b),and other parameters are set as= = = = γ,and ωm=20γ

Secondly,in the non-equilibrium case T1≠ T2,we assume that T1=Tm+ΔT/2 and T2=Tm-ΔT/2,where Tmis the average temperature and ΔT represents the temperature gradient between two heat baths.For ΔT=0,which means the system is in equilibrium case,similar to the results in Fig.2(a),Fig.2(b).But for non-equilibrium case,we are more interested in the relationship between the temperature gradient ΔT of two heat baths and the steady-state entanglement of the system.As shown in Fig.3(a),at some average temperatures Tm,e.g.,Tm=2γ and Tm=2.5γ,the concurrence decreases first and then increases with the increase of the temperature gradient ΔT;in some cases,e.g.,Tm=3.5γ,4γ,4.5γ,5γ,5.5γ,the concurrence decreases when the temperature gradient ΔT increases.Therefore,we understand that the temperature gradient ΔT has a disadvantage for the entanglement.Here,we are also concerned with the critical value ΔTc,which leads to the ESD.The dependence of ΔTcon the average temperature Tmis shown in Fig.3(b).One can see that ΔTcdecreases with Tmincreasing.That is,in the low temperature,the temperature gradient has a wider range of changes so that it may be useful for improving the concurrence as shown in Fig.2(a).

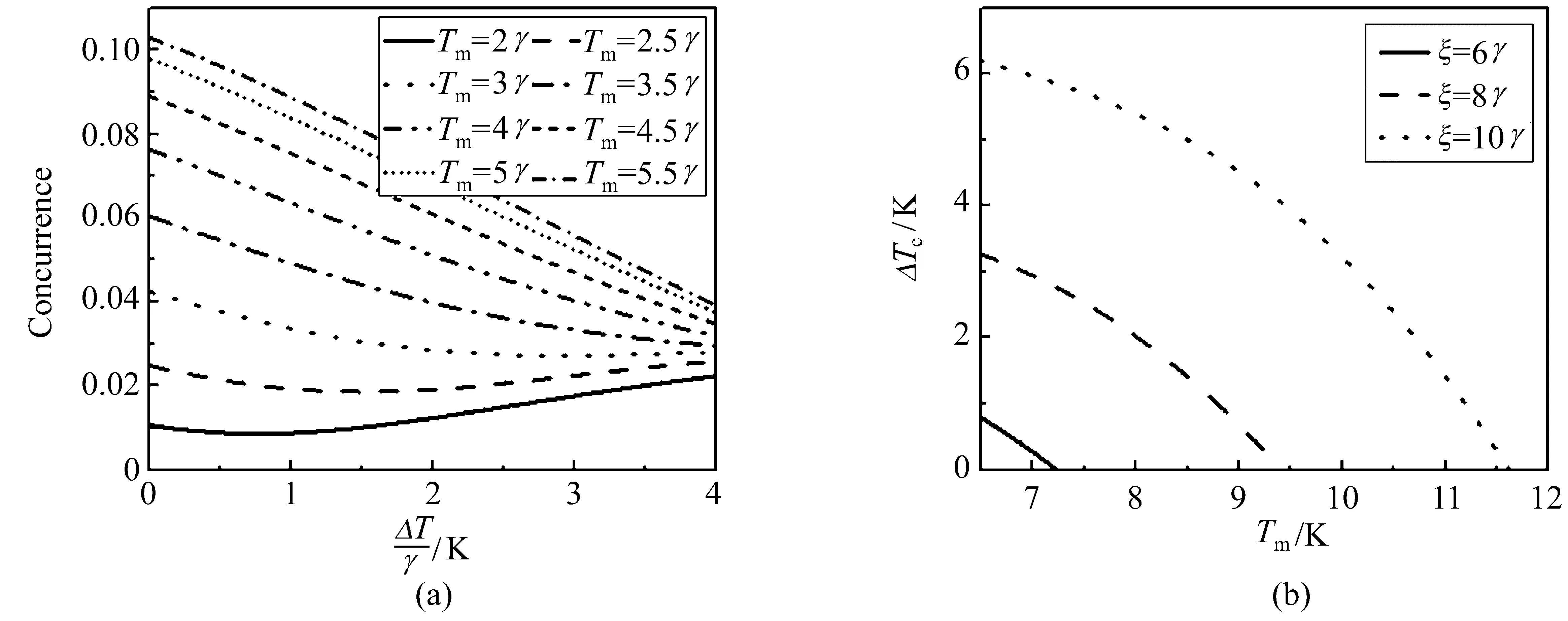
圖3 非平衡熱庫T1≠T2,(a)不同平均溫度Tm下,穩(wěn)態(tài)糾纏作為溫度梯度ΔT的函數(shù);(b)不同耦合強(qiáng)度ξ下,臨界溫度梯度ΔTc作為平均溫度Tm的函數(shù).假設(shè)(a)ξ=10γ,其他參數(shù)設(shè)為= = = = γ,ωm=20γ,Δω =10γFig.3 In non-equilibrium baths with T1 ≠ T2,the steady-state entanglement as a function of the temperature gradient ΔT of two heat baths for different average temperatures Tmis shown in(a).The critical temperature gradient ΔTcas a function of the average temperatures Tmfor different coupling strengths ξ is shown in(b).Setting ξ=10γ in(a),and other parameters are set as= = = = γ,ωm=20γ,and Δω =10γ

2.3 Heat current

From the above discussion,it can be concluded that the temperature gradient between two heat baths has a certain influence on the steady-state entanglement.Next,we further discuss the influence of coupling strength and other factors on heat current.The heat current can be defined as

Fig.4(a)shows that the variations of heat currents Qhand Qcare the function of the high temperature T1.If T1＜2,Qc＞0 means that the heat bath b releases energy through the system to the heat bath a.For T1＞2,the heat current goes in the opposite direction.At the critical temperature T1=2[the small diagram in Fig.4(a)],it means that the whole system is in equilibrium.In Fig.4(b),we obtain that the larger energy detuning Δω leads to a negative effect on the heat current Qh.In Fig.4(c),we observe that heat current Qhincreases with coupling strength ξ(temperature T1)increasing for a given T1(ξ).In Fig.4(d),when Qhis zero,the corresponding temperature is the same as that of the cool bath.The lower temperature is smaller,heat current is larger.

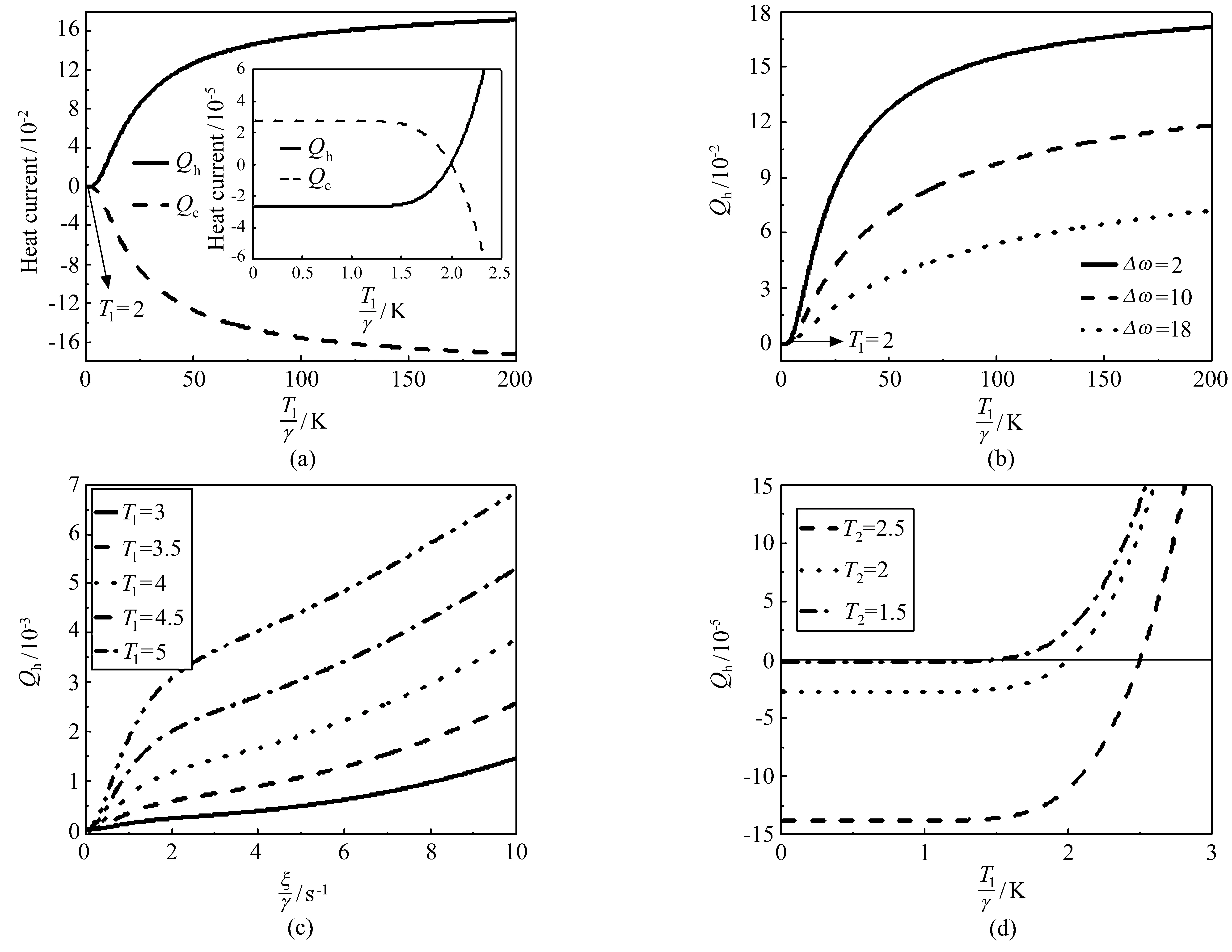
圖4 (a)熱流Qh和Qc為熱庫a的溫度T1的函數(shù);(b)不同能量失諧Δω和(d)不同的熱庫b溫度T2下,Qh作為溫度T1的函數(shù);(c)不同溫度T1下,Qh作為耦合強(qiáng)度ξ的函數(shù).假設(shè)(a),(c),(d)Δω=2;(a),(b),(d)ξ=4;(a),(b),(c)T2=2,其他參數(shù)設(shè)為====0.01和ωm=20Fig.4 Heat currents Qhand Qcare the function of the high temperature T1in(a),Qhis the function of the higher temperatures T1for different energy detunings Δω in(b)and diverse lower temperatures T2in(d).Qhis the function of the coupling strength ξ for various higher temperatures T1in(c).Setting Δω =2 in(a),(c),(d),ξ=4 in(a),(b),(d)and T2=2 in(a),(b),(c),and other parameters are set as=== =0.01 and ωm=20

3 The steady-state entanglement and heat current of the system interacting with two CHBs

In this section,we study the quantum thermalization of two coupled qubits immersed in two CHBs with different temperatures.

3.1 Equations of motion and steady-state solutions

The quantum master equation describing the evolution of the two qubits immersed in two CHBs with different temperature has the same form as Eq.(11),but the CHB case includes correlating terms.So,the master equation and correlation terms can be described as

with

3.2 Steady-state entanglement

No matter how qubits interact with two baths,the concurrence in the equilibrium case are the same as shown in Fig.2.We can draw the conclusion that the entanglement of the system is independent of the baths that qubits touch in the equilibrium case.So we are more interested in the effect of non-equilibrium CHBs on the entanglement.

In the non-equilibrium regime,we note that the concurrence firstly increases and then decreases when the average temperature Tmincreases for ΔT=0 and the optimal concurrence approximately arises in Tm=6γ,which are consist with Fig.2(a),Fig.2(b).The concurrence increases with the temperature gradient ΔT increasing when the average temperature Tmis relatively small(e.g.,for Tm=2γ,Tm=2.5γ and Tm=3γ).The concurrence decreases with ΔT increasing for the larger Tm(e.g.,for Tm=4γ,Tm=4.5γ,Tm=5γ and Tm=5.5γ).We conclude that non-equilibrium condition with ΔT ≠ 0 is beneficial to the concurrence under the low temperature,whereas the optimal entanglement appears at ΔT=0 for the high temperature.Here,we are also concerned with the critical value ΔTc,in which ESD occurs.In Fig.5(b),we note that ΔTcdecreases with Tmon matter what the value of ξ is.And the temperature gradient has a wider range of changes than ΔTcin Fig.3(b).

圖5 非平衡熱庫T1≠T2,(a)不同平均溫度Tm下,穩(wěn)態(tài)糾纏作為溫度梯度ΔT的函數(shù);(b)不同耦合強(qiáng)度ξ下,臨界溫度梯度ΔTc作為平均溫度Tm的函數(shù).假設(shè)(a)ξ=10γ,其他參數(shù)設(shè)為====γ,ωm=20γ和Δω =10γFig.5 In non-equilibrium baths with T1 ≠ T2,the steady-state entanglement as the function of the temperature gradient ΔT of two heat baths for various average temperatures Tmis shown in(a).The critical temperature gradient ΔTcas a function of the average temperatures Tmfor different ξ is shown in(b).Setting ξ=10γ in(a),and other parameters are set as= = = = γ,ωm=20γ,and Δω =10γ

3.3 Heat current

AsshowninFig.6(a),theflowdirectionoftheheatcurrentissimilartothatinFig.4(a),exceptfornumerical differences.In Fig.6(b),the figures show that the larger Δω is beneficial when T1＜ 10,while the larger Δω leads to a negative effect when T1＞ 10.In Fig.6(c),heat current Qhdecreases when coupling strengths ξ increases.Raising the temperature T1or lowering the temperature T2will increase the temperature gradient between two heat baths,resulting in a greater change in heat current in Fig.6(c),Fig.6(d).Fig.6(d)is only a slight variation in the value as shown in Fig.4(d).Selecting the appropriate coupling strength,energy detuning and temperature gradient can make the heat current between two heat baths exist,and thus the steady-state entanglement of the system can be obtained.

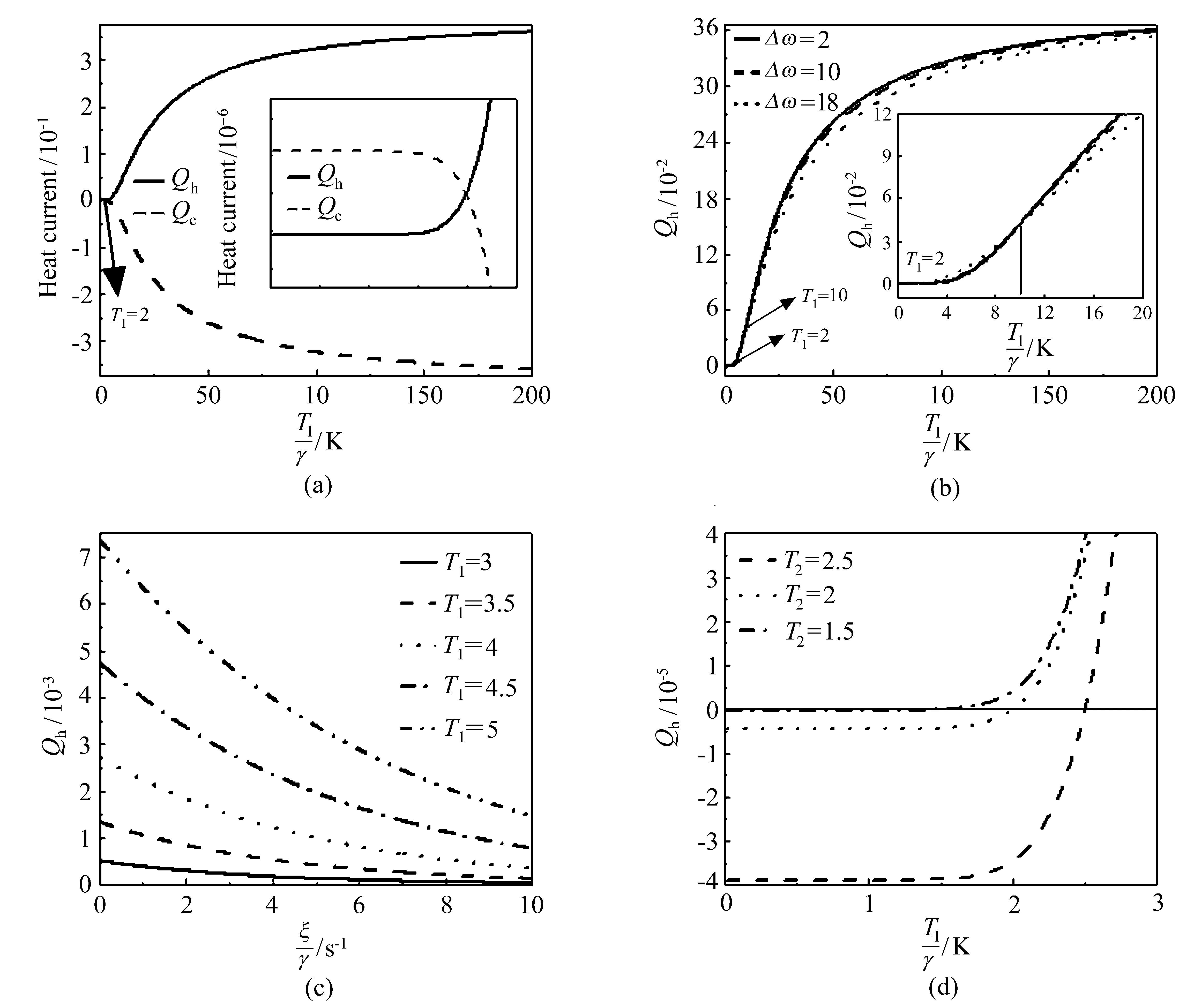
圖6 (a)熱流Qh和Qc為熱庫a的溫度T1的函數(shù);(b)不同能量失諧Δω和(d)不同的熱庫b溫度T2下,Qh作為溫度T1的函數(shù);(c)不同溫度T1下,Qh作為耦合強(qiáng)度ξ的函數(shù).假設(shè)(a),(c),(d)Δω=2;(a),(b),(d)ξ=4;(a),(b),(c)T2=2,其他參數(shù)設(shè)為====0.01和ωm=20Fig.6 Heat currents Qhand Qcare the function of the high temperature T1in(a),Qhis the function of the higher temperatures T1for different energy detunings Δω in(b)and diverse lower temperatures T2in(d).Qhis the function of the coupling strength ξ for various higher temperatures T1in(c).Setting Δω =2 in(a),(c),(d),ξ=4 in(a),(b),(d)and T2=2 in(a),(b),(c),and other parameters are set as = = ==0.01 and ωm=20

4 Conclusion

In conclusion,we investigated the steady-state entanglement and the heat current of two coupled qubits in two independent heat baths and in two common heat baths,respectively.The effects of coupling strength,energy detuning and temperature gradient on the entanglement and heat current are mainly considered when the two heat baths are in equilibrium and non-equilibrium.In the equilibrium bath,enhancing the coupling strength and increasing the energy detuning as well as raising the temperature gradient are beneficial to the enhancement of the entanglement,and the critical temperature Tcincreases with the energy detunings Δω (coupling strengths ξ)for a given ξ(Δω).In the non-equilibrium bath,the entanglement is enhanced(suppressed)by the temperature gradient for the low(high)average temperature,and the critical temperature gradient ΔTcdecreases with the average temperature Tmincreasing.Subsequently,we study the relationship between the heat current and the energy detuning,the coupling strength and the temperature of bath.The stable heat current between two heat baths can be obtained by selecting appropriate coupling strength,energy detuning and temperature gradient.When two qubits are in contact with two independent heat baths,the energy detuning has a negative effect on the heat current,and heat current increases when the coupling strengths increases for a given temperature.While two qubits interact with two common heat baths,the energy detuning has a positive(negative)effect on the heat current in the low(high)temperature and heat current decreases with coupling strengths increasing.It is helpful to analyze or understand the influence of thermal environment on two or multi-entangled system,and the best parameters can be selected to keep the system maximally entangled.