ENERGY CONSERVATION FOR SOLUTIONS OF INCOMPRESSIBLE VISCOELASTIC FLUIDS?
(何一鳴)
School of Mathematics and Statistics,Central China Normal University,Wuhan 430079,China E-mail:18855310582@163.com
Ruizhao ZI (訾瑞昭)?
School of Mathematics and Statistics&Hubei Key Laboratory of Mathematical Sciences,Central China Normal University,Wuhan 430079,China E-mail:rzz@mail.ccnu.edu.cn
Key words Incompressible viscoelastic fluids;weak solutions;energy conservation
1 Introduction
In this paper,we consider the issue of energy conservation for solutions to the incompressible viscoelastic flows
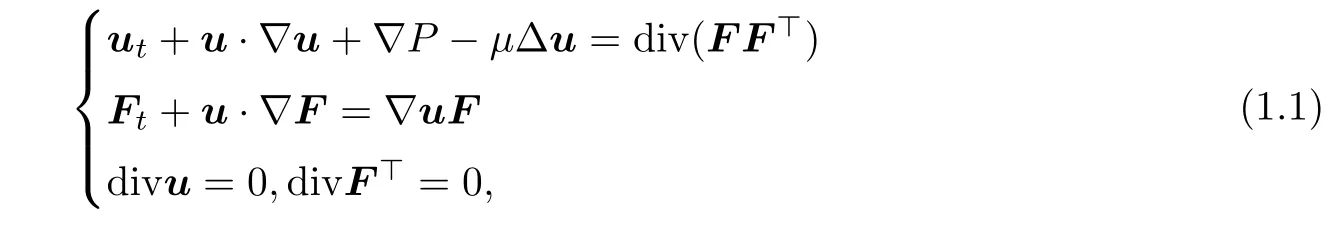
d
×d
matrices with detF=1(that is the incompressible condition),FF
=τ
,which is the Cauchy-Green strain tensor,P
is the pressure of the fluid,andμ
≥0 is the coefficient of viscosity.For a given velocity field u(x,t
)∈R,one de fines the flow mapx
(t,X
)by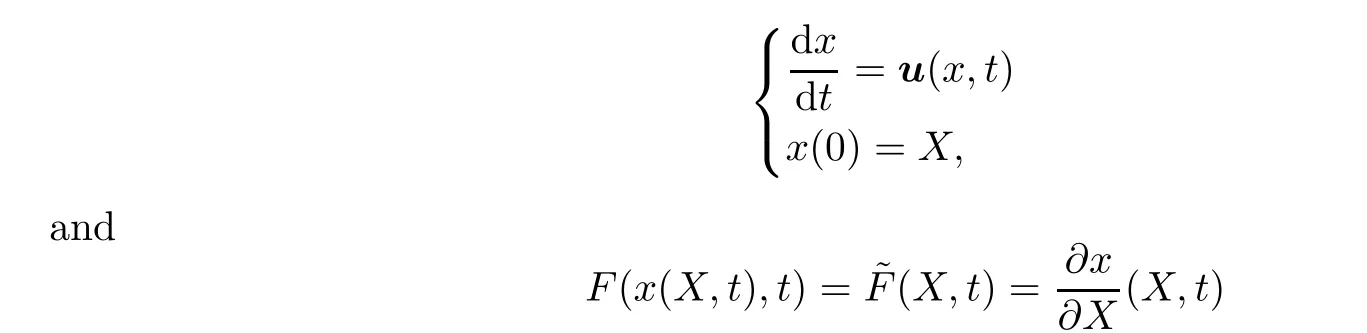
x
(t,X
).Moreover,the initial data satisfy
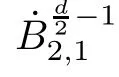
μ
=0,the global existence in 3D whole space was established by Sideris and Thomases in[37,38]by using the generalized energy method of Klainerman[24].The 2D case is more delicate,and here the first non-trivial long time existence result was obtained by Lei,Sideris and Zhou[27]by combining the generalized energy method of Klainerman and Alinhac’s ghost weight method[2].Lei[26]proved the 2D global well-posedness of the classical solution by exploring the strong null condition of the system in the Lagrangian coordinates.Wang[39]gave a new proof in Euler coordinates.In this paper,we are interested in the energy conservation of weak solutions to incompressible viscoelastic fluids(1.1).More precisely,our question is how badly behaved(u,
F)can keep the energy conservation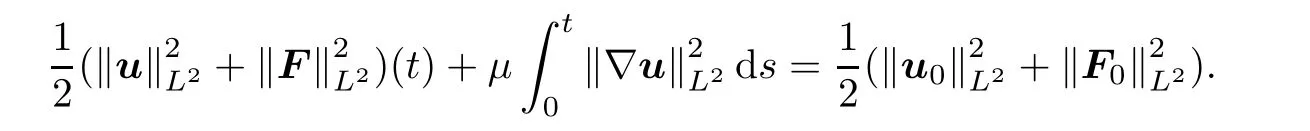
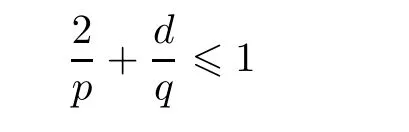
d
is the dimension of space.In[35],Shinbrot showed that Serrin’s condition can be replaced by a condition independent of dimension,that is,u∈L
(0,T
;L
(?)),where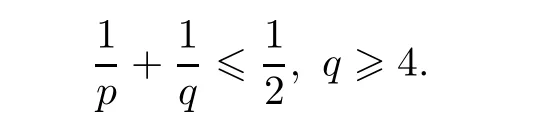
Recently,Yu,in[40],gave a new proof of Shinbrot’s result.

Before proceeding any further,we would like to give some notations which will be used throughout the paper.
Notations
(1)Throughout the paper,C
stands for a positive harmless“constant”.The notationf
?g
means thatf
≤Cg
.(2)Let(divM)=?
M
,whereM
is ad
×d
matrix;(?u)=?
u
;Fis the transpose of the matrix F=(F,
···,
F),where Fis thej
-th column of F.
De finition 1.1
We say that(u,
F)is a weak solution of(1.1)with Cauchy data(1.2),if it satis fies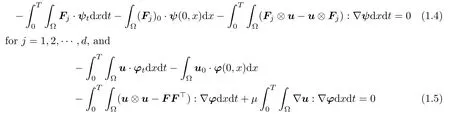
,
ψ∈C
([0,T
)×?;R)with compact support,and div?=0.Our main results are stated as follows:
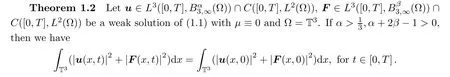
Remark 1.3
Compared with the general result in[21],our result in Theorem 1.2 allowsu
andF
to possess different regularities.Our second result is built on R.

μ>
0 in the torus T.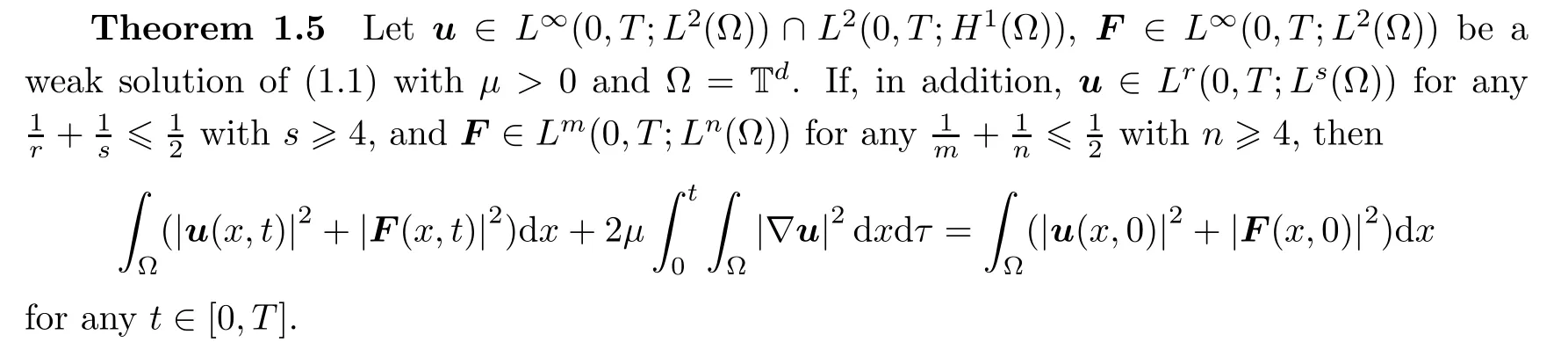
Remark 1.6
It would be very interesting to investigate the boundary effect,and we will consider this problem in the near future.2 Preliminaries
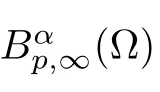
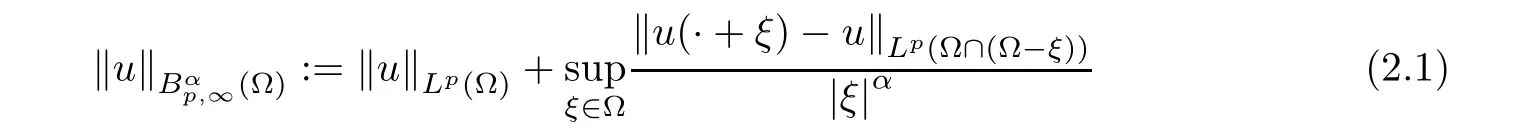
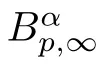

Corollary 2.2
For two functionsu,v
,let us denote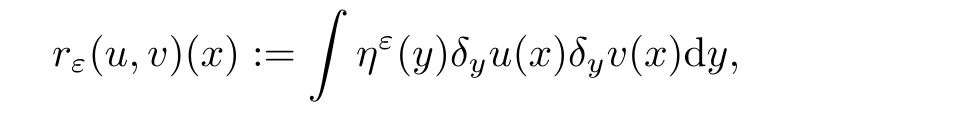
δ
u
(x
)=u
(x
?y
)?u
(x
).Then the identity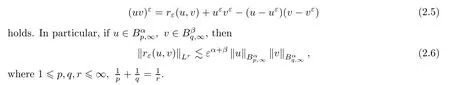
Remark 2.3
(2.5)is a general case of(10)in[11].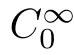

Then,the following is true:

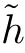
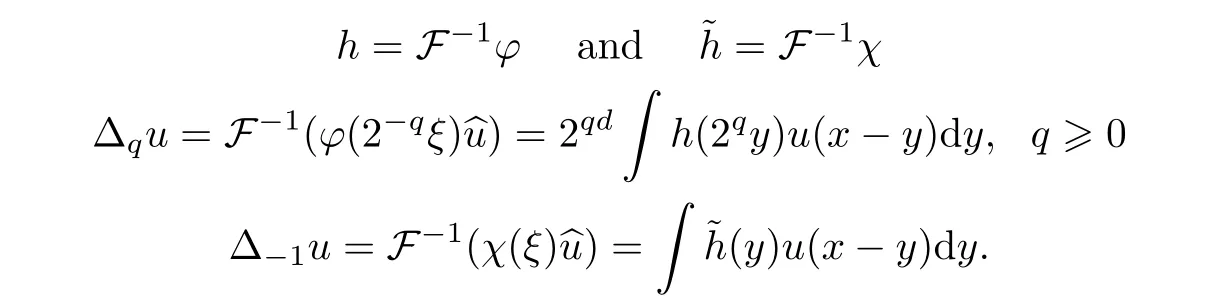
S
u
is de fined by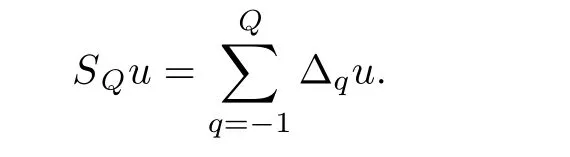
We then have
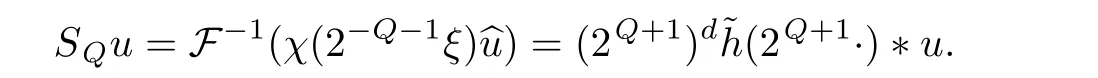
With the aid of the Little wood-Paley decomposition,Besov spaces can also be de fined as follows:
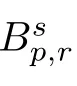
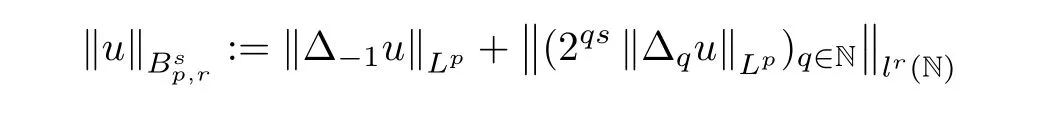
is finite.
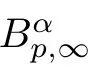
The following lemma describes the way derivatives act on spectrally localized functions:
Lemma 2.6
(Bernstein’s inequalities[3])Letting C be an annulus and B a ball,a constantC
exists such that for any nonnegative integerk
,any couple(p,q
)∈[1,
∞]withq
≥p
≥1,and any functionu
ofL
,we have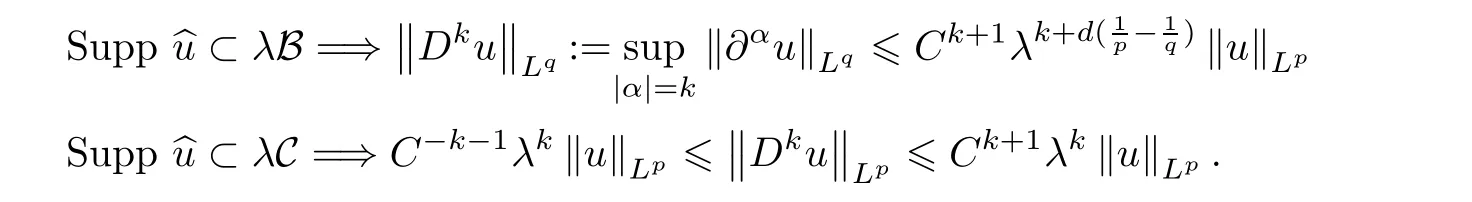
In particular,we have
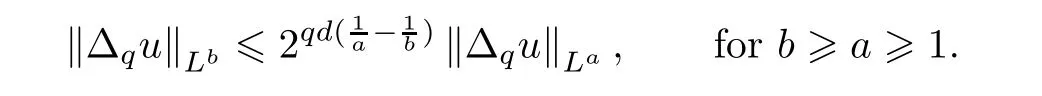
As a consequence,we have the following inclusions:
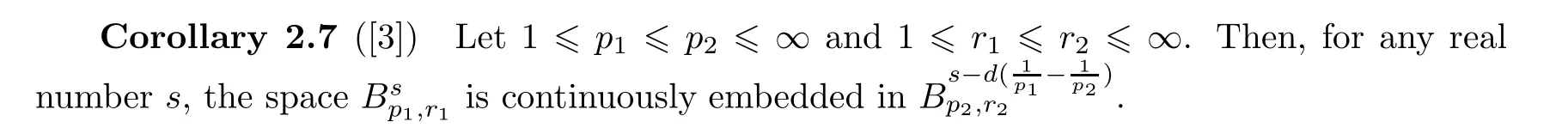
The following space was first introduced by Cheskidov et al.in[10]:
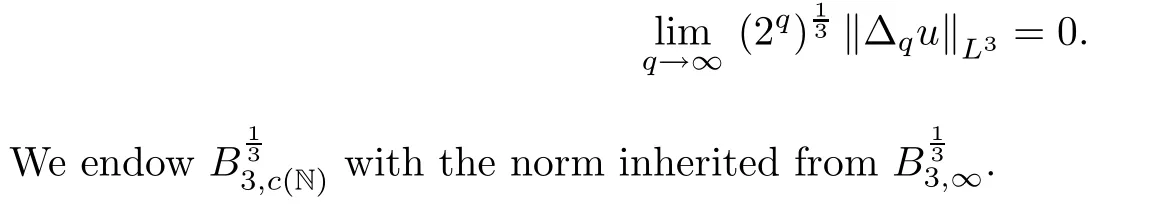
L
.For a proof of this lemma,please refer to[30].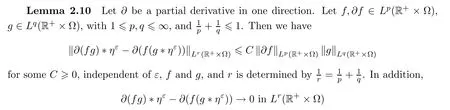
3 Proof of the Results
3.1 Proof of Theorem 1.2
We will use the summation convention for notational convenience.For the sake of simplicity,we will proceed as if the solution is differentiable in time.The extra arguments needed to mollify in time are straightforward.
Now,using(u)and(F)to test the first and second equations of(1.1),one obtains
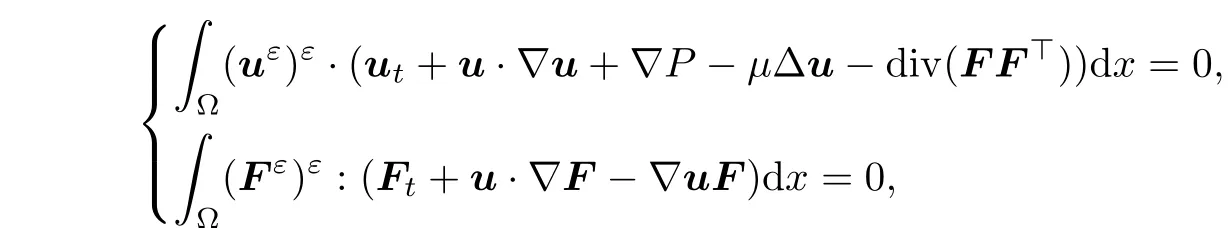
which in turn gives
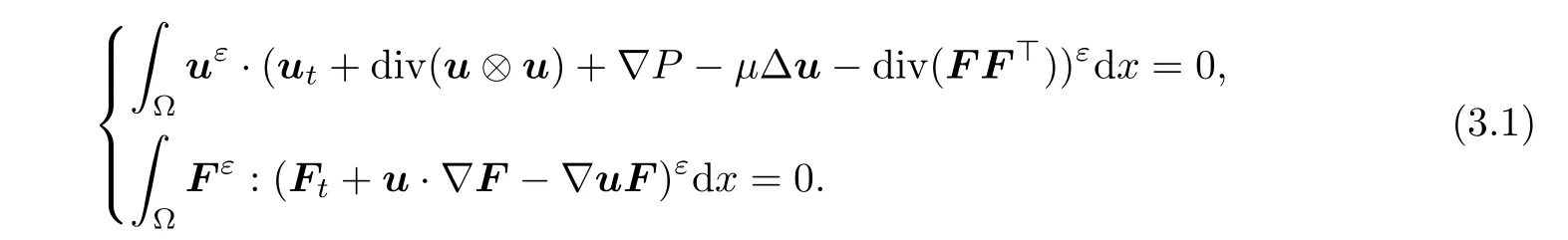
u
=0,we have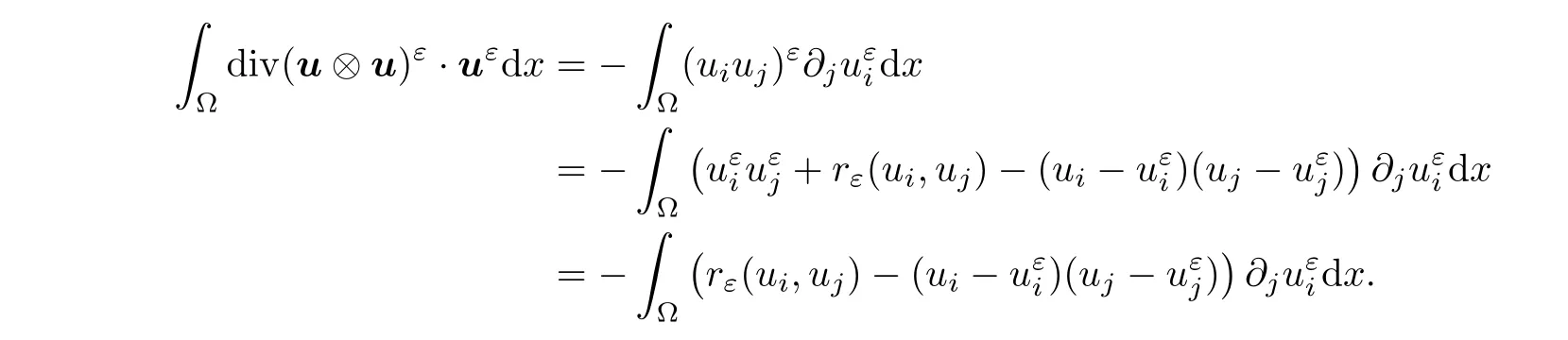
Similarly,we have
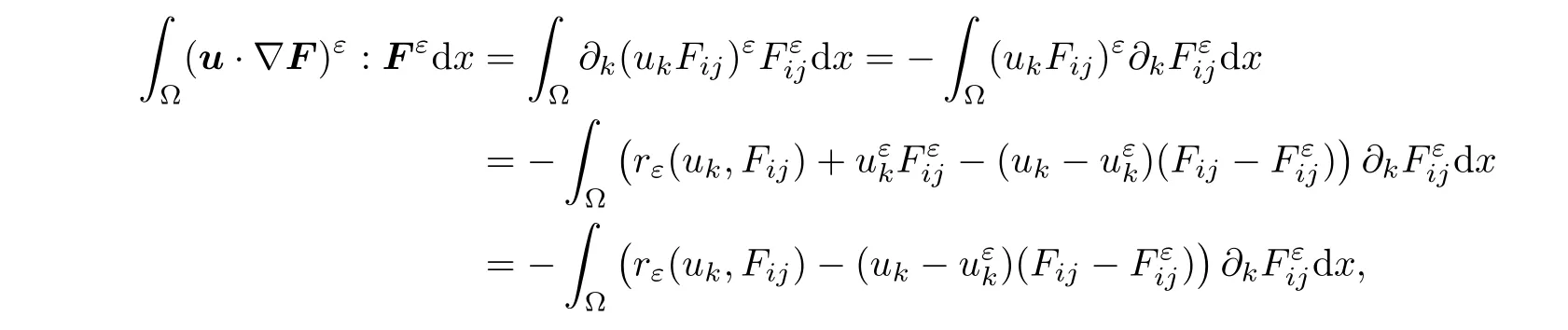
due to the fact that
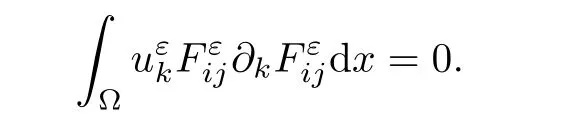
In the same way,we have
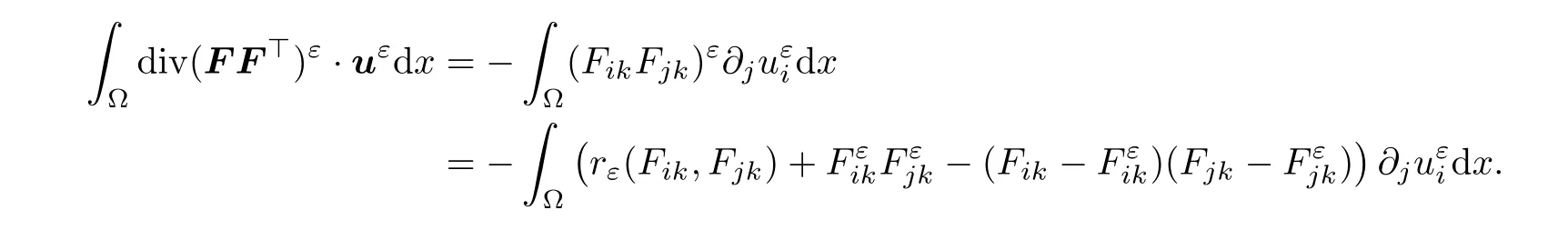
Finally,noting that divF=0,
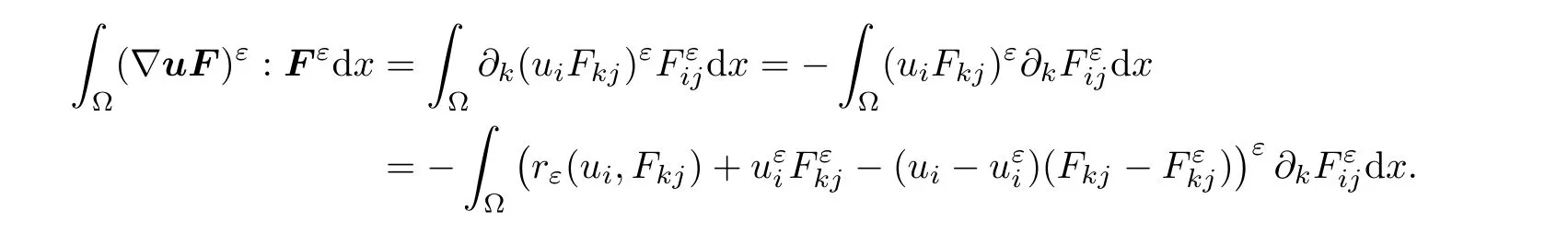
Thanks to the fact that divF=0,integrating by parts,we are led to
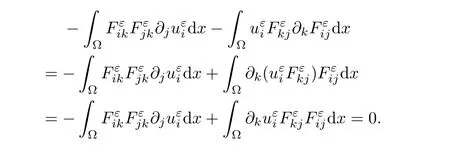
μ
=0,we get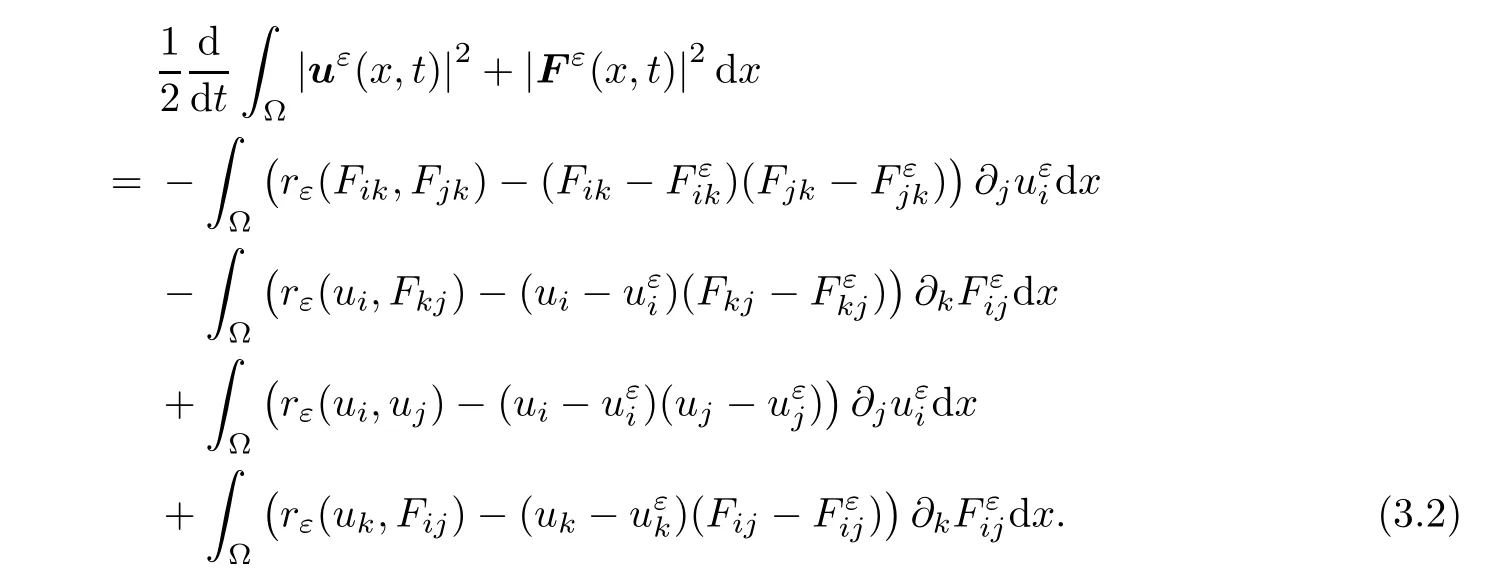
Then,integrating(3.2)w.r.t.the time variable,one deduces that
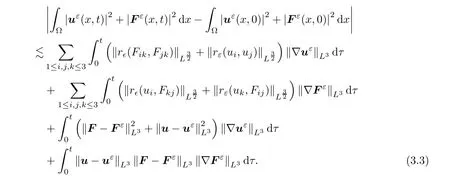
By Corollary 2.2,we have
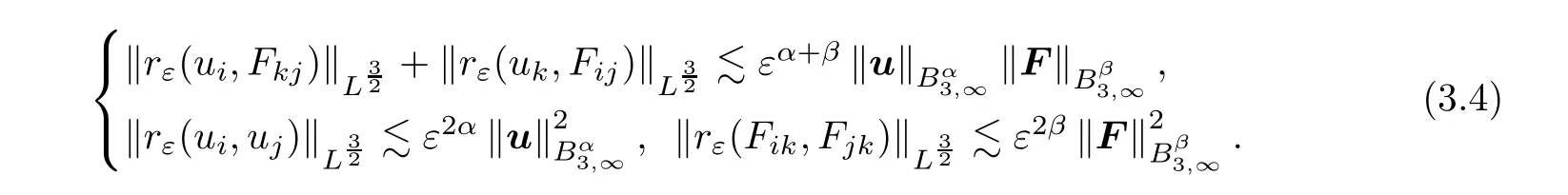
α
?1>
0,α
+2β
?1>
0,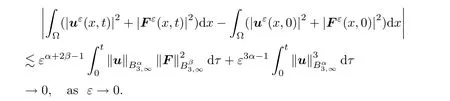
We complete the proof of Theorem 1.2.
3.2 Proof of Theorem 1.4
Let us start this subsection by introducing the following localization kernel as in[10]:
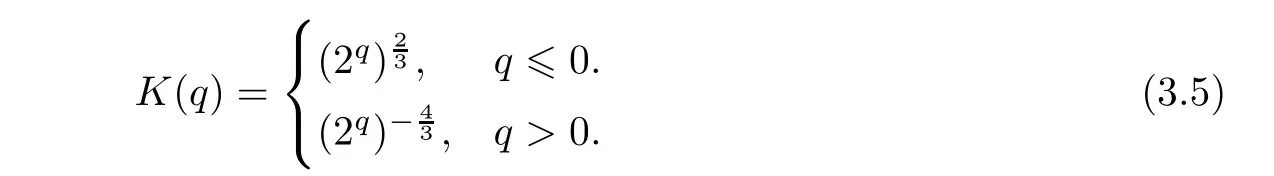
u
andF
in R,denote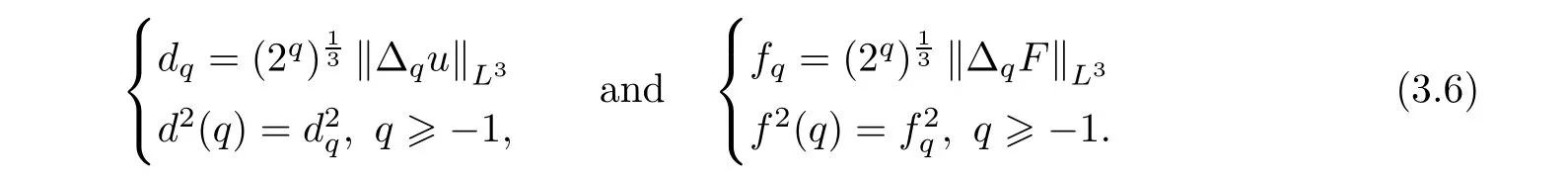
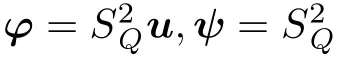
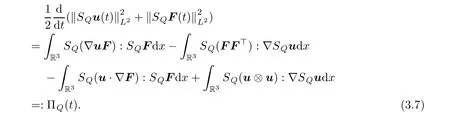
In a fashion similar to(3.2),after cancelation,we arrive at
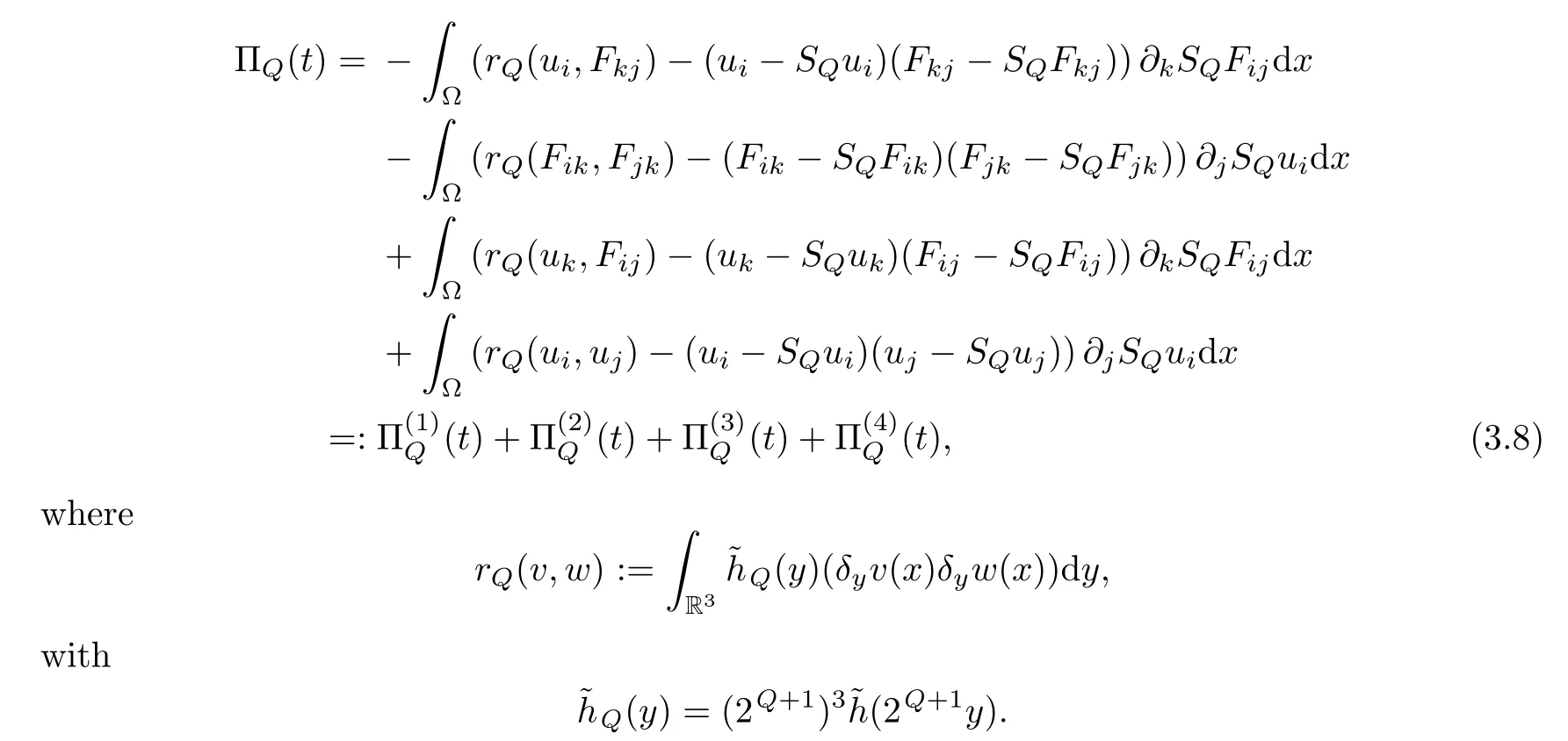
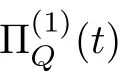
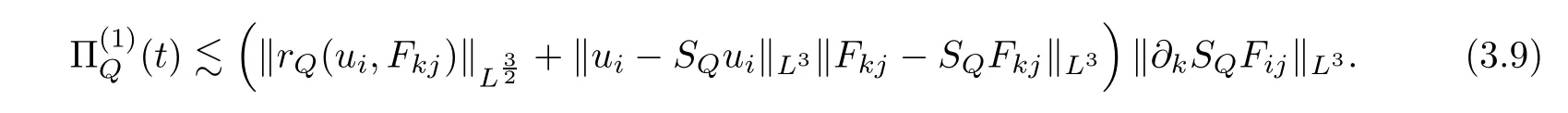
By Minkowski’s inequality,
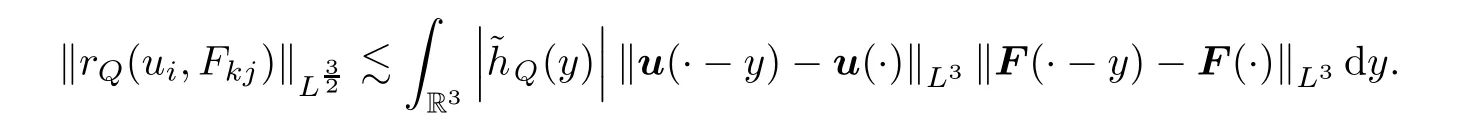
Let us now use Bernstein’s inequalities and Remark 2.8 to estimate
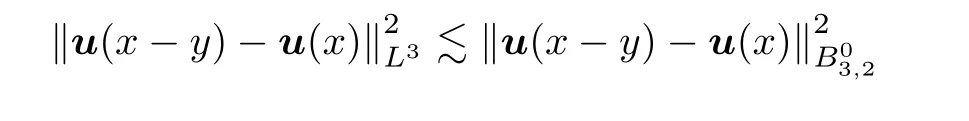
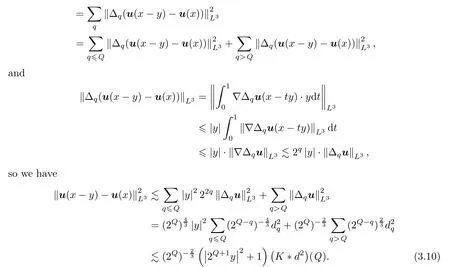
Similarly,it holds that

On the other hand,
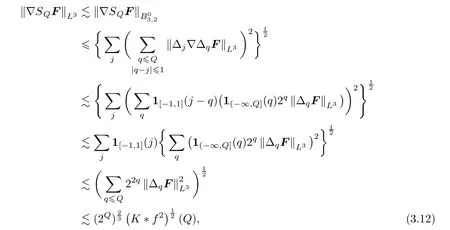
and similarly,
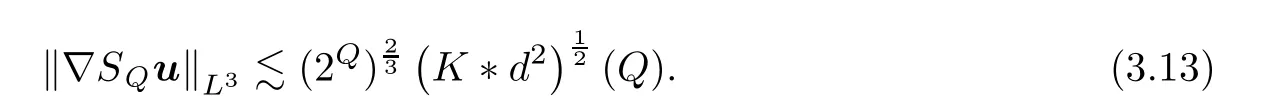
Noting that(3.10)and(3.11)also imply
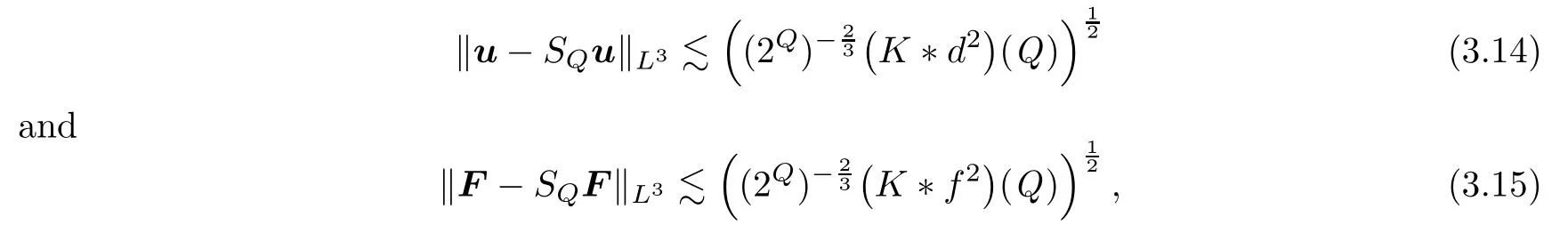
respectively,it then follows from(3.9)–(3.14)that
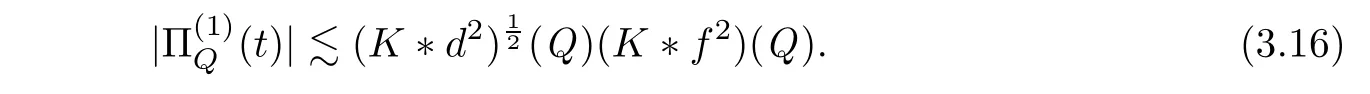
In the same manner,we have
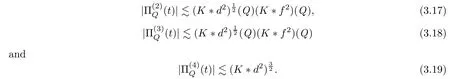
Accordingly,
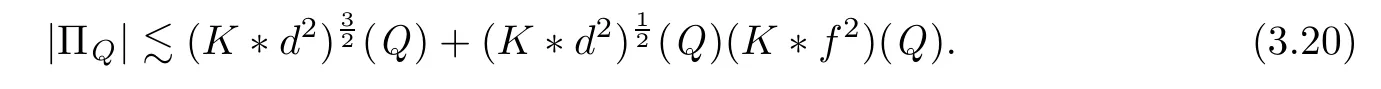
K
‖<
∞,we immediately obtain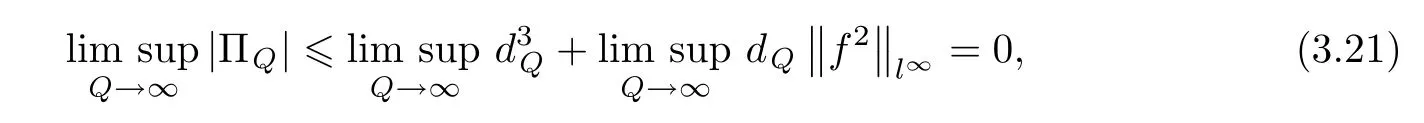
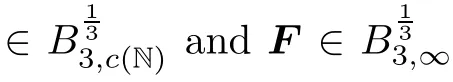
3.3 Proof of Theorem 1.5
We shall complete the proof of Theorem 1.5 by the following two steps:

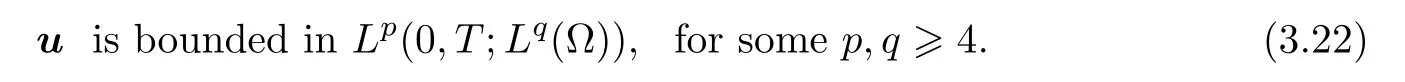
r
≥4,so we only consider the case in which 2≤r<
4 ands>
4.By interpolation,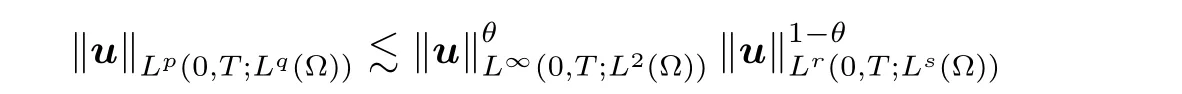
θ
∈(0,
1).It suffices to show that there exists aθ
∈(0,
1)such that
θ
satisfying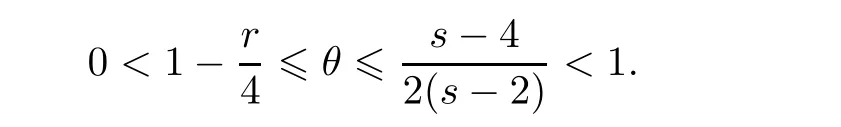
r<
4 ands>
4,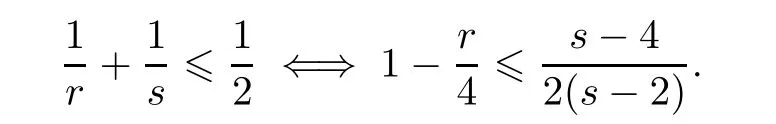

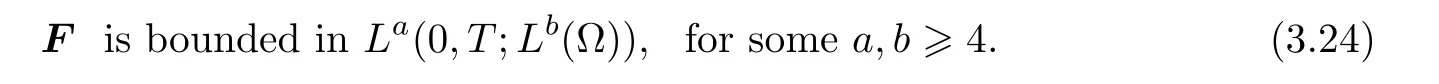
We will use(3.22)and(3.24)frequently in the next proof.
Step(II)
By(3.1),it is easy to verify that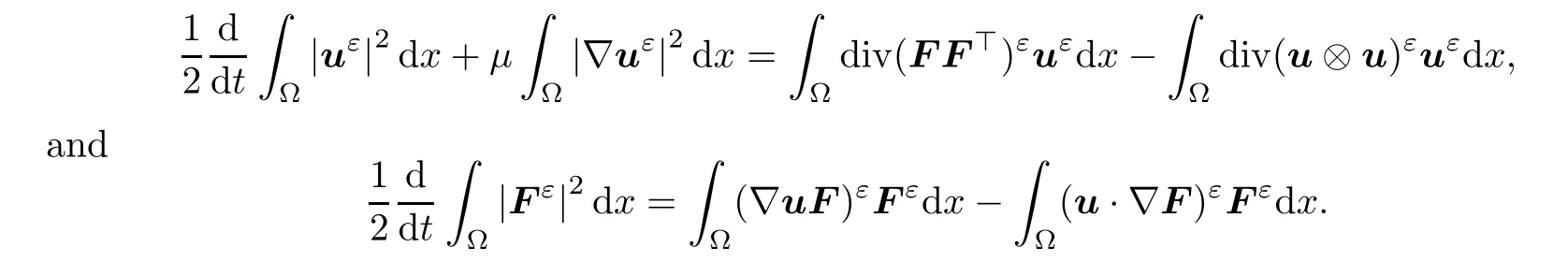
Integrating in time and adding the two equations together,we have
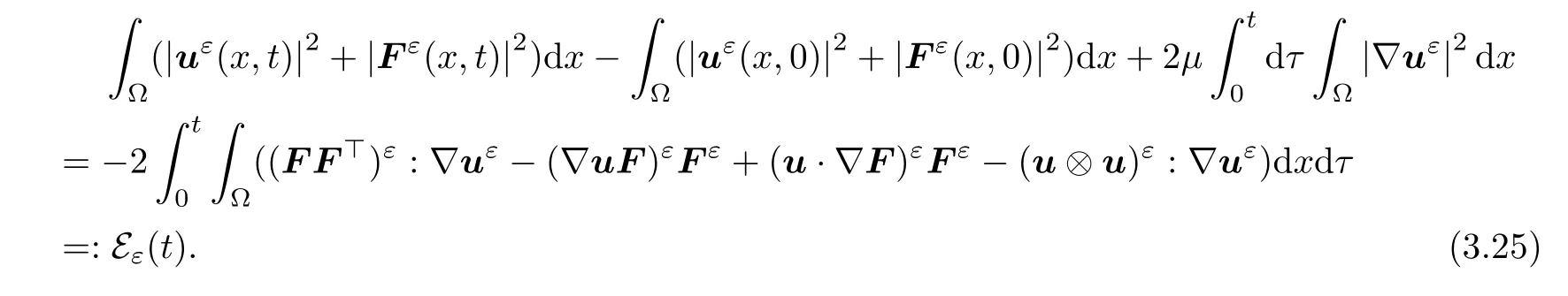
We next rewrite
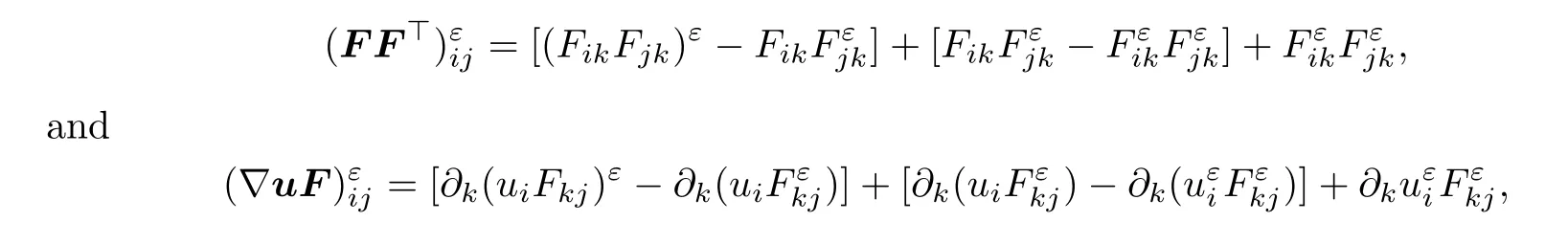
due to the fact that divF=0.Moreover,
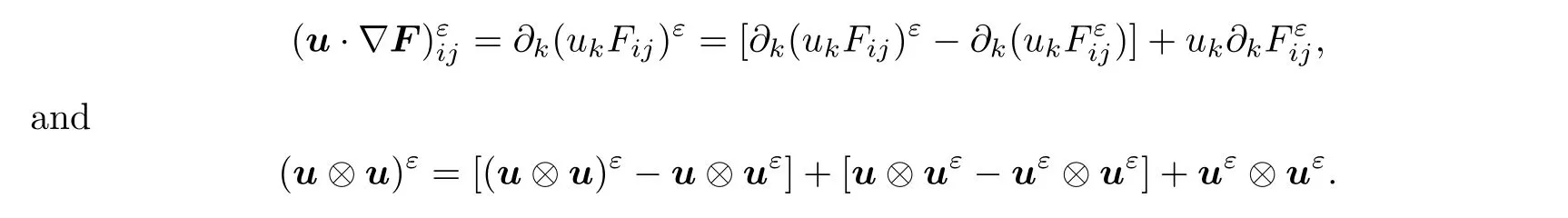
Substituting the above four equalities into(3.25),thanks to divu=0,we find that
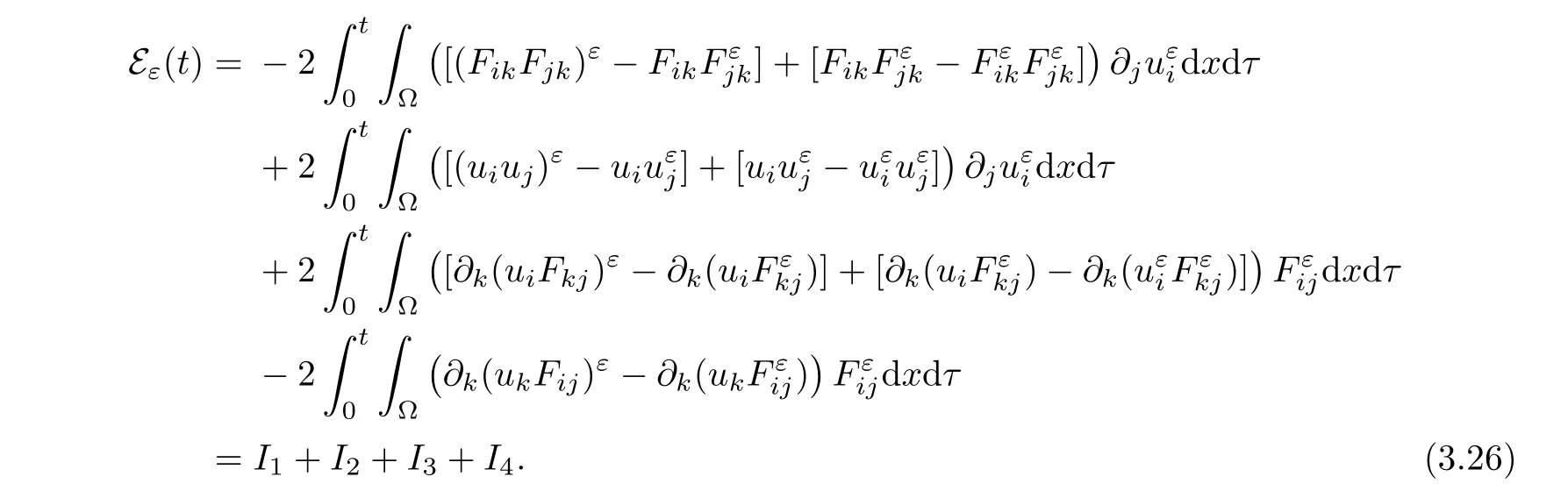
ε
tends to zero,and that
ε
→0.It follows that
In the same way,we obtain

I
,Lemma 2.10 ensures that
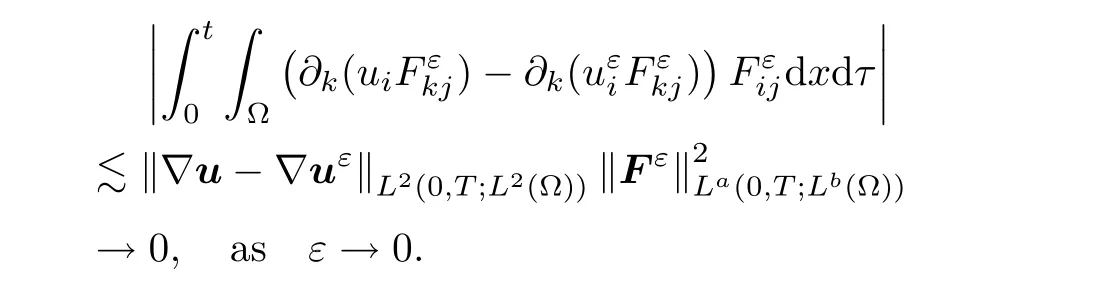
It follows that

Finally,in view of Lemma 2.10,
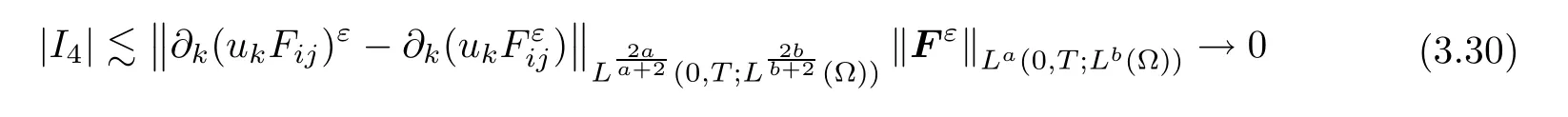
ε
→0.Lettingε
go to zero in(3.25),and using(3.27)–(3.30),we obtain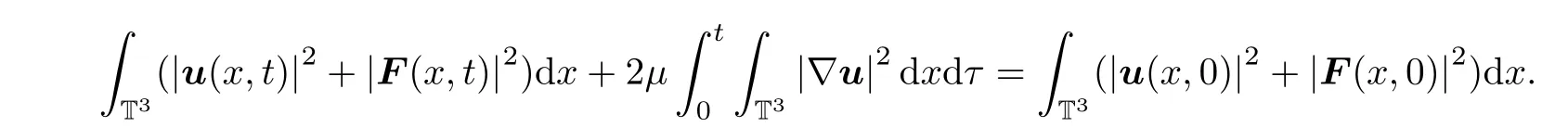
This completes the proof of Theorem 1.5.
 Acta Mathematica Scientia(English Series)2021年4期
Acta Mathematica Scientia(English Series)2021年4期
- Acta Mathematica Scientia(English Series)的其它文章
- REGULARITY OF WEAK SOLUTIONS TO A CLASS OF NONLINEAR PROBLEM?
- EXISTENCE TO FRACTIONAL CRITICAL EQUATION WITH HARDY-LITTLEWOOD-SOBOLEV NONLINEARITIES?
- A DIFFUSIVE SVEIR EPIDEMIC MODEL WITH TIME DELAY AND GENERAL INCIDENCE?
- ON A COUPLED INTEGRO-DIFFERENTIAL SYSTEM INVOLVING MIXED FRACTIONAL DERIVATIVES AND INTEGRALS OF DIFFERENT ORDERS?
- CLASSIFICATION OF SOLUTIONS TO HIGHER FRACTIONAL ORDER SYSTEMS?
- JULIA LIMITING DIRECTIONS OF ENTIRE SOLUTIONS OF COMPLEX DIFFERENTIAL EQUATIONS?
