差分可辨性隱私參數(shù)的迭代分配方法*

任旭杰, 尚 濤, 劉建偉

北京航空航天大學(xué) 網(wǎng)絡(luò)空間安全學(xué)院, 北京100083

1 引言

隨著大數(shù)據(jù)和云計算時代的到來, 各種數(shù)據(jù)挖掘算法得到了飛速發(fā)展. 例如聚類算法, 通過幾輪迭代將一個數(shù)據(jù)集劃分為多個簇, 同一簇中的數(shù)據(jù)相似性較高, 不同簇之間相似性較低, 以此實現(xiàn)對數(shù)據(jù)的無標簽分類, 可以對數(shù)據(jù)隱含未知信息進行挖掘, 對大數(shù)據(jù)的潛在價值有重要作用. 但在聚類為數(shù)據(jù)帶來應(yīng)用前景的同時, 也出現(xiàn)了一些敏感信息的隱私泄露問題. 近些年, 對隱私保護的研究已成為學(xué)術(shù)界的熱門方向.

2006 年, Dwork[1]提出差分隱私的概念, 具有嚴格的數(shù)學(xué)理論基礎(chǔ), 不依賴攻擊者的背景知識, 把對敏感數(shù)據(jù)的保護程度參數(shù)化為一個隱私預(yù)算值?; 2005 年, Blum 等人[2]在SuLQ 平臺上設(shè)計實現(xiàn)了一種差分隱私k-means 算法, 在計算聚類中心的過程中, 在求和函數(shù)和計數(shù)函數(shù)的查詢結(jié)果中加入少量噪聲來保證隱私, 但是該算法并未給出設(shè)置隱私預(yù)算?的方式. 2006 年, Aggarwal 等人[3]提出先對原始數(shù)據(jù)集進行聚類操作, 用簇中心替換所有記錄連同簇特征一起發(fā)布實現(xiàn)隱私保護的方法, 但這種處理方式使大多數(shù)數(shù)據(jù)遭到破壞, 降低了數(shù)據(jù)可用性. 2007 年, Nissim[4]提出PK-means 算法, 給出了如何計算誤差下界和函數(shù)敏感度的方法, 使最終聚類模型滿足差分隱私的要求. 2011 年, Dwork[5]分析了k-means 算法中敏感度的詳細計算方法, 并給出了隱私預(yù)算?的設(shè)置方式. 2013 年, 李楊等人[6]提出IDPk-means算法, 該算法經(jīng)過一個對初始中心點的處理, 解決了經(jīng)過差分隱私加噪后的初始中心點偏離過大導(dǎo)致聚類結(jié)果不可用的問題. 2016 年, 鄭劍等[7]提出了一種針對線性回歸的分析的差分隱私算法Diff-LR, 將線性回歸模型的目標函數(shù)分解, 并將隱私預(yù)算分配為兩部分對子函數(shù)進行擾動, 降低了算法的敏感度, 提升了模型精度. 2018 年, 楊庚等[8]提出一種面向差分隱私的隱私預(yù)算分配和數(shù)據(jù)發(fā)布方法, 利用泊松機制實現(xiàn)了差分隱私預(yù)算在數(shù)據(jù)發(fā)布中的應(yīng)用, 可以達到隱私預(yù)算無窮分配的目的. 2019 年, 尚濤等[9]提出了一種等差隱私預(yù)算分配方法, 相比等比隱私預(yù)算分配, 該方法在保證了模型可用性的同時提升了精度, 但等差分配的方式不能實現(xiàn)隱私預(yù)算的任意分配, 只能應(yīng)用于迭代次數(shù)固定或已知的模型訓(xùn)練中.

2012 年, Lee 和Clifton[10]認為差分隱私不關(guān)注攻擊者背景知識, 只關(guān)注個體對數(shù)據(jù)庫輸出影響, 這不符合隱私相關(guān)的法律定義, 因此提出差分可辨性的概念, 它提供與差分隱私相當?shù)碾[私保護能力, 旨在限制個體被重新識別的概率, 隱私參數(shù)的設(shè)置也為從業(yè)者提供了一個簡單的參數(shù)化方法. 2014 年, 歐洋伶[11]提出新的隱私保護算法Margin-Jump, 為非交互型數(shù)據(jù)列聯(lián)表提供ρ-差分可辨性隱私保護. 通過隨機替換數(shù)據(jù)集的敏感屬性值, 以ρ-差分可辨性作為隱私保護模型. 目前, 對基于差分可辨性的聚類算法研究仍有較大空白.

2020 年, Shang 等人[12]研究了差分可辨性的指數(shù)機制應(yīng)用于非數(shù)值型數(shù)據(jù), 并通過數(shù)學(xué)證明得出差分可辨性的組合性質(zhì), 基于組合性質(zhì)在聚類算法的迭代過程中添加噪聲, 在MapReduce 框架上進行聚類,最終得到滿足ρ-差分可辨性的聚類模型. 但是, 文獻[12] 的方法中添加噪聲的方式基于差分可辨性與差分隱私的映射關(guān)系, 即將差分隱私的隱私參數(shù)設(shè)置為ρ的函數(shù), 并沿用了每輪隱私預(yù)算為上一輪一半的分配方式, 這并未很好地利用差分可辨性的性質(zhì), 本質(zhì)上仍是差分隱私噪聲. 因此, 本文提出基于差分可辨性組合性質(zhì)推出的隱私參數(shù)分配方法, 可以滿足隱私參數(shù)在迭代輪數(shù)固定情況下的平均分配和迭代輪數(shù)不固定時的任意分配, 并且最終得到的模型仍滿足ρ-差分可辨性的要求.

本文結(jié)構(gòu)如下. 第2 節(jié)介紹了差分可辨性的相關(guān)定義及組合性質(zhì). 第3 節(jié)給出了差分可辨性參數(shù)分配方法在聚類中的應(yīng)用. 第4 節(jié)是實驗分析, 驗證本文方法的可行性. 最后, 第5 節(jié)總結(jié)全文, 并討論未來可能的研究方向.

2 相關(guān)知識

Lee 和Clifon[10]認為,?-差分隱私的定義存在一定缺陷: 隱私預(yù)算?是評估安全性的指標, 它旨在限制鄰近數(shù)據(jù)集輸出結(jié)果的差異, 很難將其直接與個體可識別的概念聯(lián)系在一起. 它不符合人們對于隱私安全的理解和相關(guān)法律對隱私的定義. 因此, Lee 和Clifton 提出ρ-差分可辨性的概念,ρ-差分可辨性也可提供強大的隱私保證, 其隱私參數(shù)ρ限制的是重新識別某個個體屬于原始數(shù)據(jù)集的概率, 這與人們對隱私保護的法律意義相符.ρ-差分可辨性假設(shè)攻擊者擁有背景知識L=,D′是原數(shù)據(jù)庫D的相鄰數(shù)據(jù)庫, 即D ?D′=vx,U為所有可能的vx的全集, ID′為D′中所有記錄的標識符集合. 定義I(vi)為記錄vi的標識符或身份信息.

定義1 (ρ-差分可辨性) 給定一個查詢函數(shù)f, 隨機機制M是滿足ρ-差分可辨性的, 當且僅當?D′=D ?vi, 且vi ∈U ?D′, 有

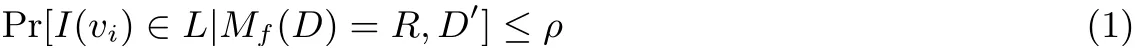
則Δf為查詢函數(shù)f的全局敏感度.

給定查詢函數(shù)f的敏感度, 可借助拉普拉斯機制實現(xiàn)ρ-差分可辨性.

文獻[12] 證明了差分可辨性和差分隱私具有類似的組合性質(zhì), 借助這些組合性質(zhì), 可以在聚類算法中實現(xiàn)差分可辨性.

推論2 (并行組合性) 假設(shè)有n個機制M1,M2,··· ,Mn, 機制Mi(i ∈[1,n]) 提供ρi-差分可辨性,Di是輸入數(shù)據(jù)集D中互不相交的子集, 機制序列Mi(Di) 提供(minρi)- 差分可辨性.

并行組合性說明了,如果有n個隨機機制M1,M2,··· ,Mn,他們均滿足差分可辨性,其中機制Mi(i ∈[1,n]) 提供ρi-差分可辨性. 對一個數(shù)據(jù)集D進行劃分后得到n個互不相交的子集D1,D2,··· ,Dn, 機制Mi對某一子集Di作用, 最終得到的模型序列(M1(D1),M2(D2),···Mn(Dn)) 滿足(minρi)- 差分可辨性.

3 差分可辨性隱私參數(shù)分配方法

3.1 迭代輪數(shù)不固定時的隱私參數(shù)分配

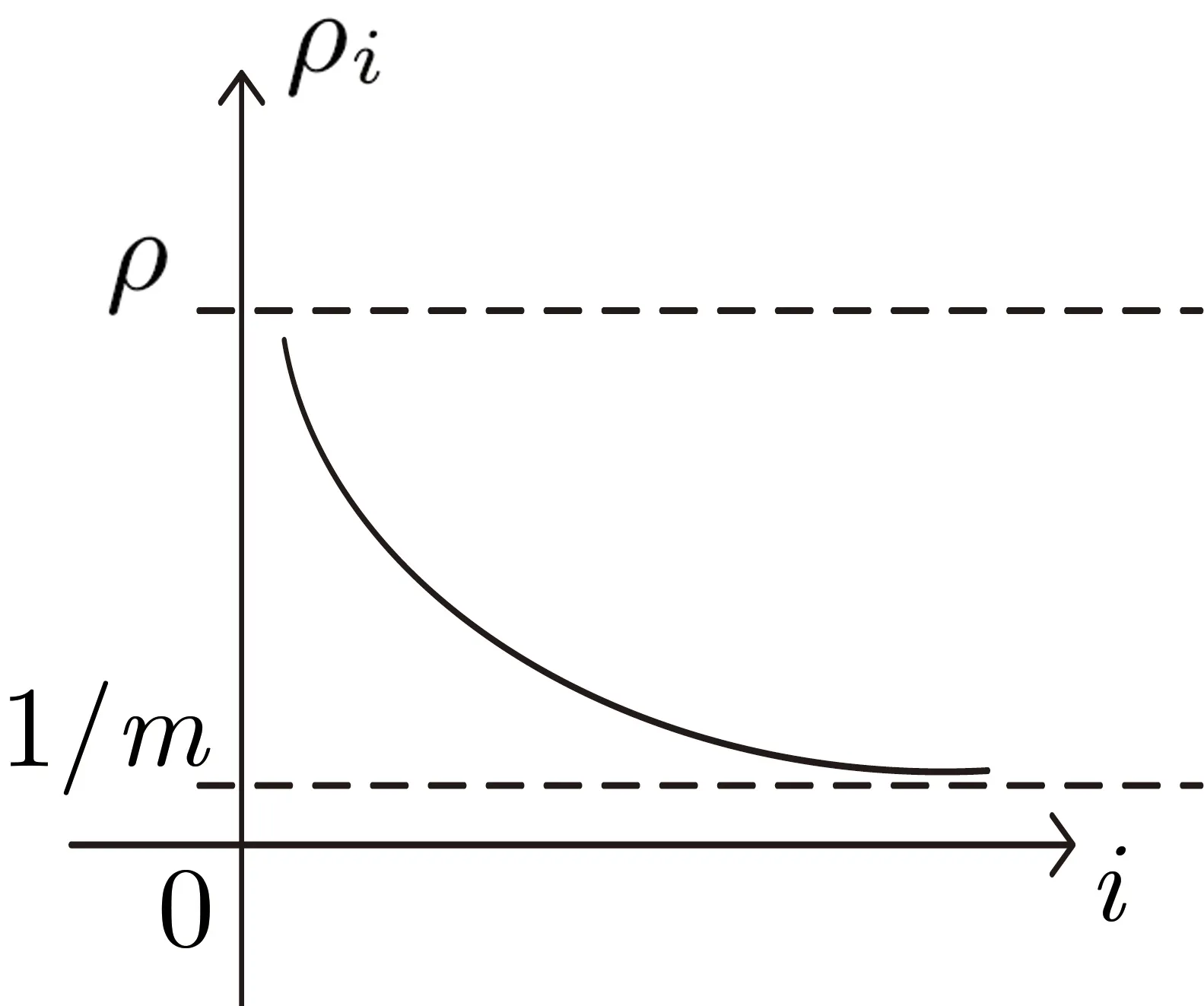
圖1 DI 參數(shù)變化趨勢Figure 1 Variation trend of parameter DI

指數(shù)部分收斂于1, 所以整個式子收斂于ρ.

該分配方法適用于任意輪數(shù)的迭代分配中, 隨著迭代輪數(shù)越多, 最終模型滿足的隱私保護能力越接近預(yù)設(shè)的ρ, 因此這是一種能夠?qū)崿F(xiàn)隱私參數(shù)無窮分配的方法. 但是迭代輪數(shù)較少時, 可能會浪費較多的隱私參數(shù)預(yù)算.

3.2 迭代輪數(shù)固定時的隱私參數(shù)分配

對于迭代輪數(shù)固定的聚類算法, 假設(shè)迭代輪數(shù)為N, 是一個固定值; 希望模型滿足的隱私參數(shù)為ρ, 根據(jù)推論1 的序列組合性, 取每輪分配的隱私參數(shù)相等, 可得每輪迭代滿足的隱私參數(shù)為

3.3 差分可辨性k-means 算法

為驗證本方法的可行性, 本節(jié)給出結(jié)合差分可辨性的k-means 算法, 具體算法如下. 輸入:d維空間[0,1]d的n個數(shù)據(jù)點p1,p2,··· ,pn, 分類個數(shù)k, 差分可辨性隱私參數(shù)ρ, 迭代輪數(shù)閾值N(可選);

輸出:k個聚類中心點c1,c2,··· ,ck.

上述過程第5) 到7) 步循環(huán)執(zhí)行, 直到簇的劃分不再變化, 或迭代次數(shù)達到某一閾值停止.

根據(jù)差分可辨性的序列組合性, 每輪迭代運算滿足差分可辨性, 那么迭代完成后的整體模型仍滿足差分可辨性. 對于加入隱私保護的聚類算法, 由于隱私參數(shù)ρ在迭代過程中的遞減, 添加的拉普拉斯噪聲會逐漸增大, 導(dǎo)致聚類中心點偏移較大, 從而使迭代進入死循環(huán)或使最終的聚類結(jié)果喪失可用性. 文獻[1] 中提出的差分隱私預(yù)算分配方法也有類似的特性. 解決辦法是對迭代輪數(shù)設(shè)置一個較小的閾值, 才能保證較好的可用性.

4 實驗分析

采用大數(shù)據(jù)集和小數(shù)據(jù)集兩組數(shù)據(jù)集進行聚類測試. 小數(shù)據(jù)集是來自KEEL 的banana 數(shù)據(jù)集, 通過兩種屬性將5300 組數(shù)據(jù)劃分為兩個類別, 用于生成可視化的聚類結(jié)果查看分類的性能. 大數(shù)據(jù)集實驗所用數(shù)據(jù)集來自UCI 機器學(xué)習(xí)庫中的magic gamma telescope, 共19 020 條數(shù)據(jù), 11 個特征, 用于對第3 節(jié)中的隱私參數(shù)分配方法進行驗證實驗, 同時與表1 中提到的方法進行性能對比. 實驗環(huán)境為Windows 7 64 bit 操作系統(tǒng), 開發(fā)語言為Python 3.7. 評價聚類性能好壞的指標為F-measure.F-measure 由常用于評價數(shù)據(jù)挖掘結(jié)果的指標準確率P(Precision) 和召回率R(Recall) 組成, 其計算值可用于評價聚類結(jié)果的效用. 準確率P和召回率R是主要參數(shù),F-measure 大小與算法聚類結(jié)果和準確聚類結(jié)果的相似性成正比,F-measure 越大, 表明兩個聚類結(jié)果的相似性越高, 最大值為1.F-measure 可通過下列公式計算.

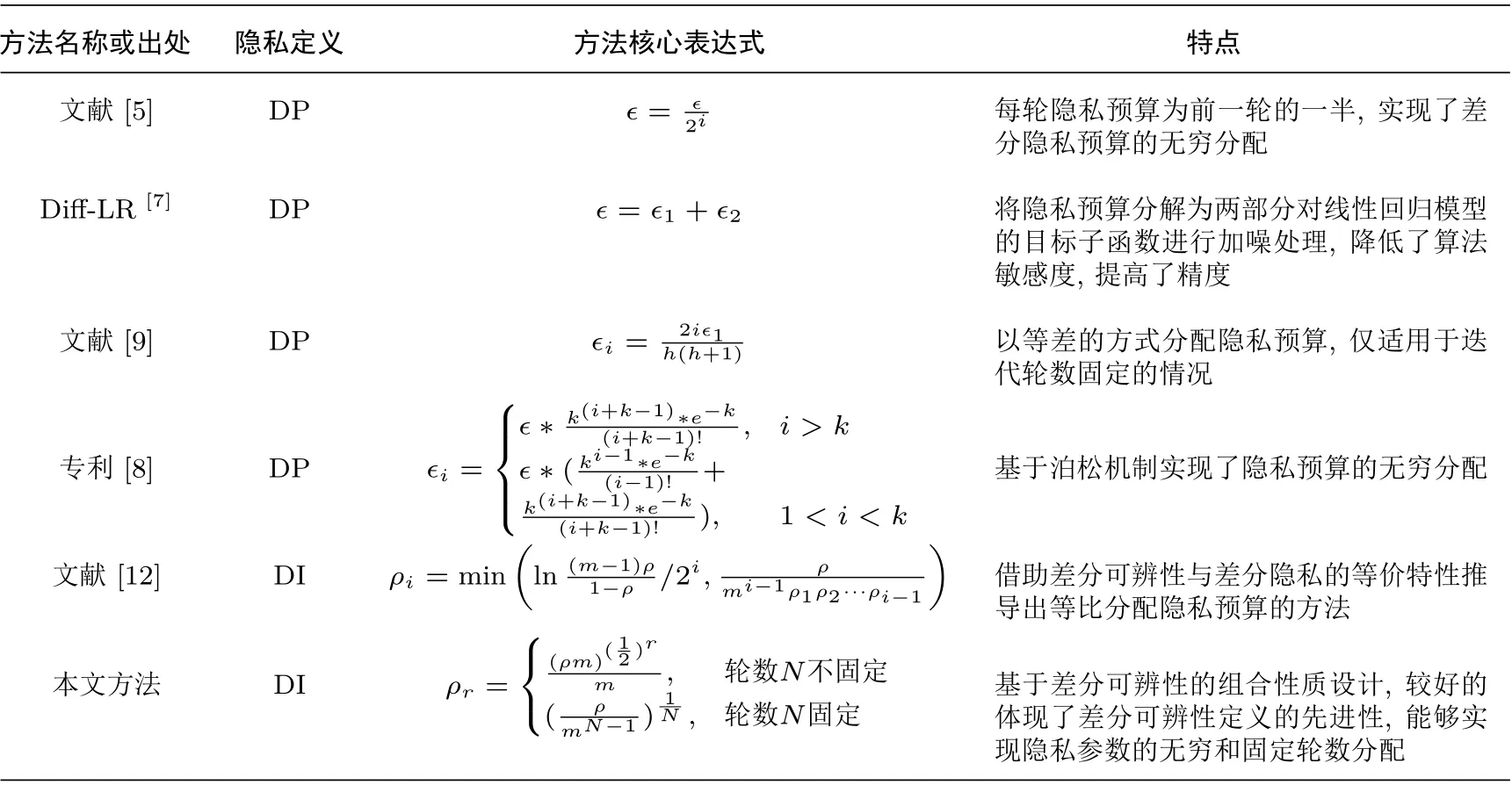
表1 不同隱私參數(shù)分配方法Table 1 Different privacy parameter allocation methods

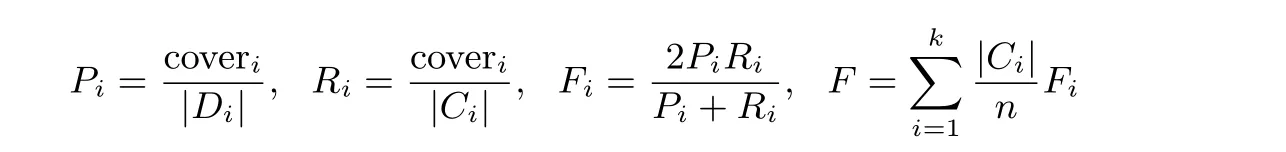
Pi和Ri(1≤k) 是第i個聚類的準確率和召回率, 聚類個數(shù)為k.Ci和Di分別表示數(shù)據(jù)集C和D的第i個聚類,|Ci| 和|Di| 為聚類Ci和Di中數(shù)據(jù)記錄數(shù)目, coveri是聚類Ci和Di中相同數(shù)據(jù)記錄數(shù)目, 計算各個聚類的F-measure 值Fi, 由各個聚類的Fi值加權(quán)平均得到指標F.

4.1 對小數(shù)據(jù)集的聚類實驗

4.1.1 未進行加噪處理的k-means 聚類

實驗設(shè)置k=2. 首先進行不加噪聲處理的k-means 聚類, 結(jié)果如圖2 所示.

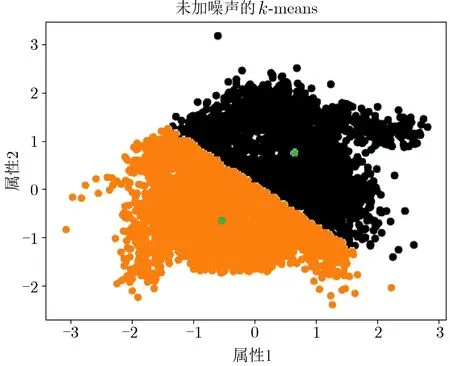
圖2 未經(jīng)加噪處理的k-means 聚類結(jié)果Figure 2 k-means cluster without noise

通過兩種不同的顏色區(qū)分兩種不同類別(某種顏色并不代表特定的類, 僅作類的區(qū)分使用). 兩個聚類中標出的點為聚類迭代過程最終產(chǎn)生的類中心點. 實驗最終聚類模型的F-measure 值計算為48%.

4.1.2 差分隱私k-means 聚類實驗結(jié)果

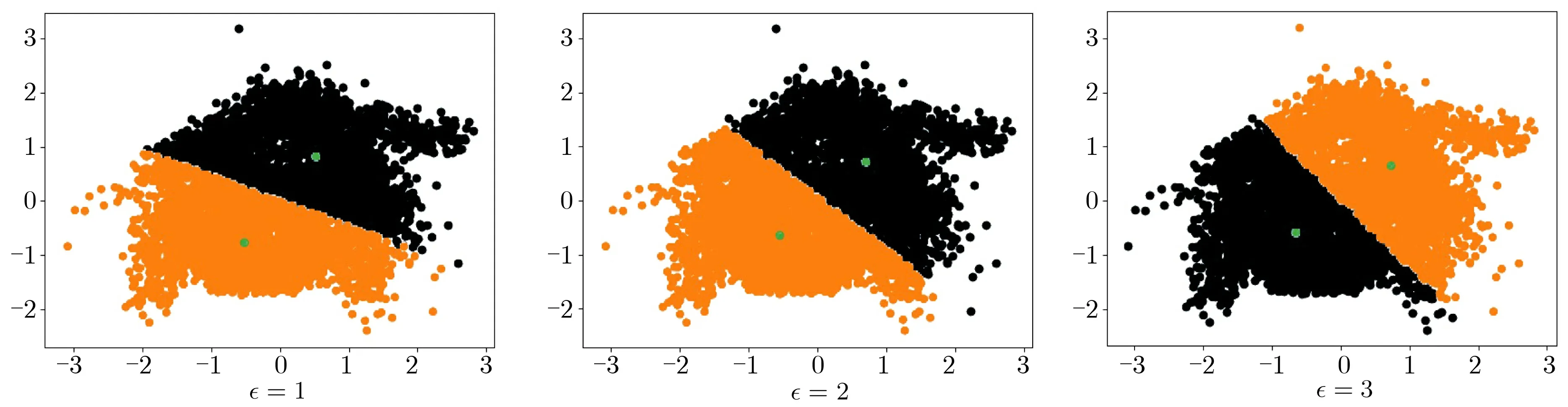
圖3 差分隱私k-means 聚類結(jié)果Figure 3 k-means cluster with noise DP

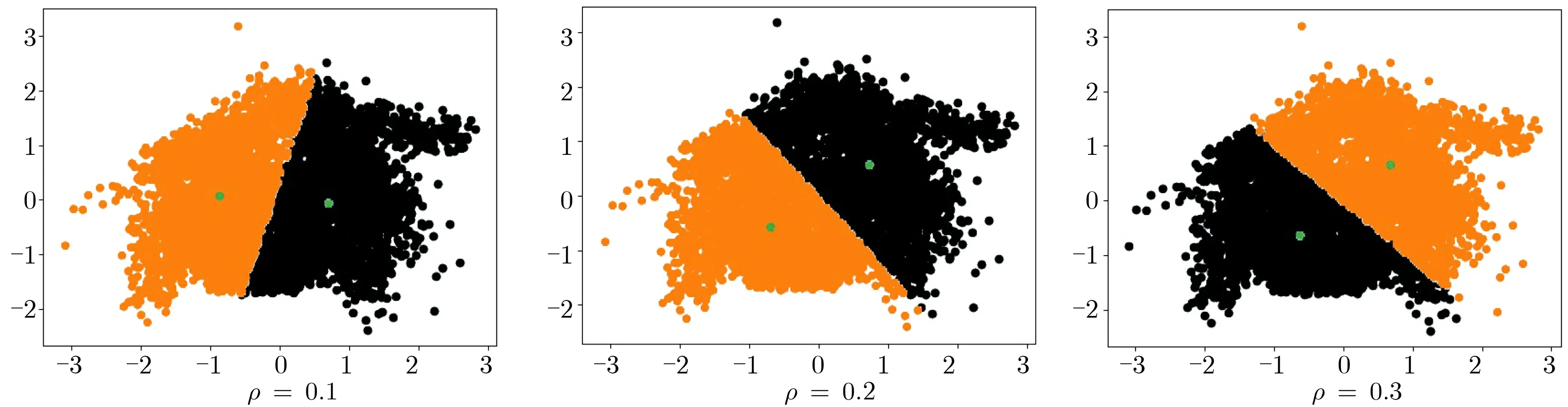
圖4 差分可辨性k-means 聚類結(jié)果Figure 4 k-means cluster with noise DI

根據(jù)第3 節(jié)中給出的隱私參數(shù)分配方法, 以ρ= 0.1 為例, 每輪隱私參數(shù)ρi= 0.003 16,0.000 56,0.000 24,0.000 15,0.000 12. 根據(jù)推論1, 最終模型滿足0.080 58-差分可辨性, 顯然也滿足0.1-差分可辨性,但因迭代輪數(shù)較少而產(chǎn)生了隱私參數(shù)預(yù)算的浪費.

實驗結(jié)果表明, 隱私參數(shù)ρ越小, 模型失真程度越高, 這與理論期待的情況吻合. 當設(shè)置合適的ρ值時, 聚類模型仍滿足一定的可用性.

4.2 對大數(shù)據(jù)集進行k-means 聚類實驗

數(shù)據(jù)集較小時, 對聚類過程中的參數(shù)進行處理可能無法很好體現(xiàn)出對聚類結(jié)果的影響, 因此本節(jié)對較大的數(shù)據(jù)集進行聚類測試. 使用表1 中列出的幾種隱私參數(shù)分配方法, 對數(shù)據(jù)集進行k-means 聚類, 設(shè)置k=11, 此后分別添加差分隱私噪聲和差分可辨性噪聲并計算F-measure. 實驗結(jié)果如圖5 和圖6 所示.

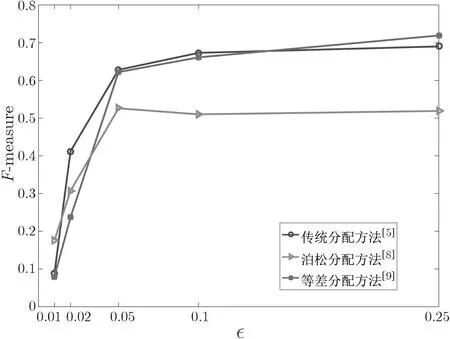
圖5 大數(shù)據(jù)集差分隱私k-means 聚類結(jié)果Figure 5 k-means cluster of big dataset with noise DP

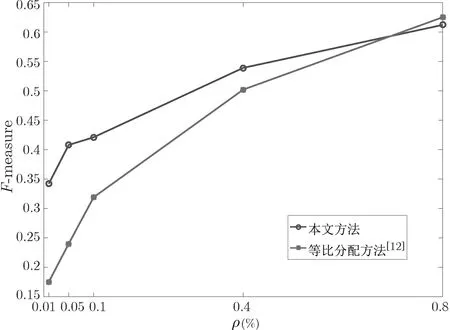
圖6 大數(shù)據(jù)集差分可辨性k-means 聚類結(jié)果Figure 6 k-means cluster of big dataset with noise DI

實驗結(jié)果顯示, 隨著隱私參數(shù)的增大, 差分隱私和差分可辨性方法表現(xiàn)出類似的性質(zhì),F-measure 值都出現(xiàn)了上升, 這與理論設(shè)想情況吻合. 差分可辨性方案分類表現(xiàn)最佳的對應(yīng)F-measure 約為0.6, 略低于差分隱私方案的0.7, 一定程度上保持聚類的可用性.

如圖6 所示, 在與文獻[12] 的方法對比中, 使用本文方法進行的k-means 聚類性能明顯較高.

4.3 迭代輪數(shù)對模型性能的影響

由于隱私參數(shù)在迭代過程中的逐輪遞減, 迭代的同時添加的噪聲也將逐步增大. 因此若不對迭代輪數(shù)進行限制, 到迭代后期對模型添加的噪聲將非常大, 從而對聚類性能產(chǎn)生影響. 本小節(jié)將通過設(shè)置不同k-means 模型構(gòu)建的迭代輪數(shù), 觀察模型性能變化, 討論迭代輪數(shù)對模型性能的影響. 在本節(jié)實驗中, 設(shè)置差分可辨性隱私參數(shù)ρ=0.8, 實驗結(jié)果如圖7 所示.

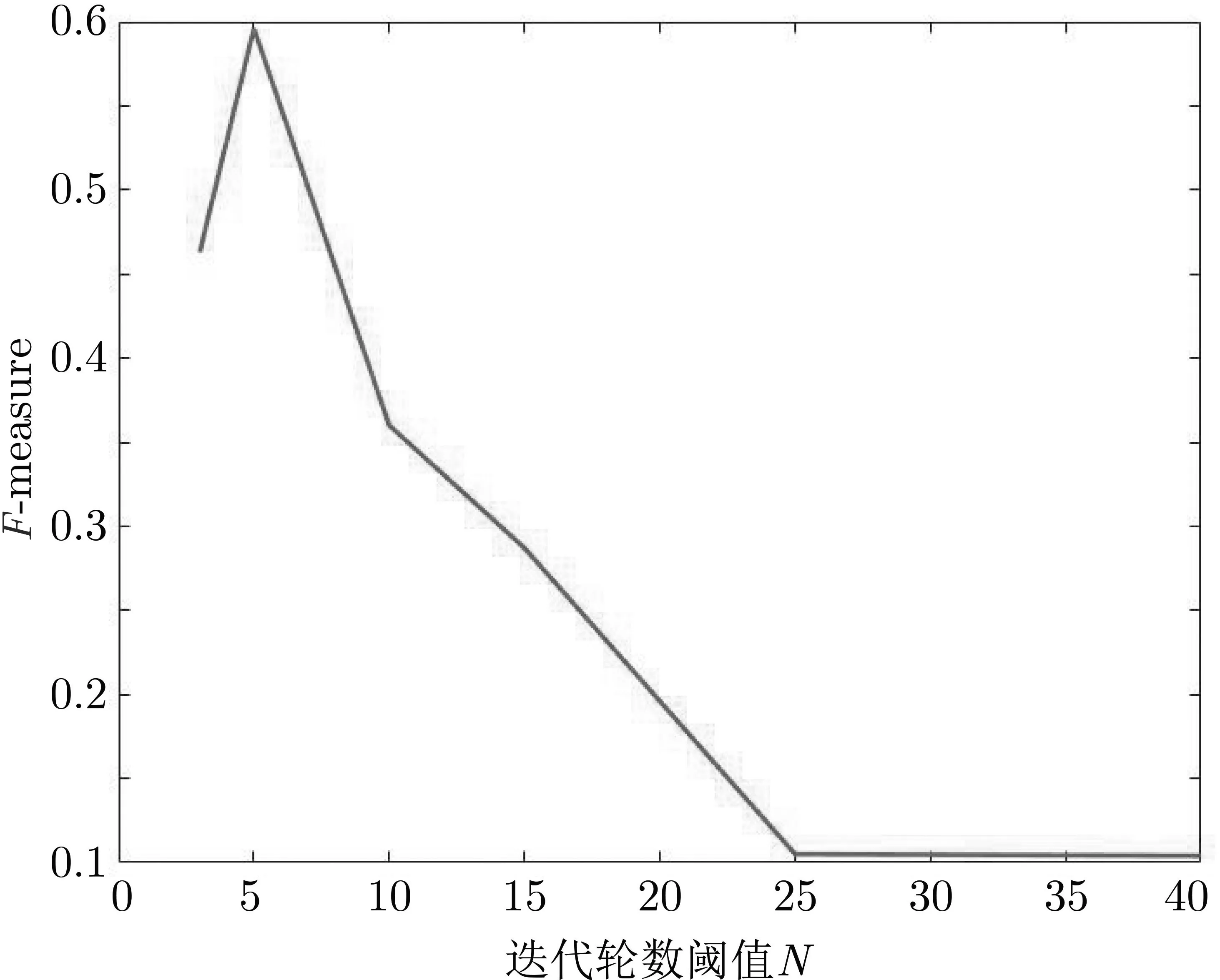
圖7 迭代閾值對模型性能的影響Figure 7 Effect of iteration round threshold on model performance

根據(jù)實驗結(jié)果, 當?shù)啍?shù)設(shè)置一個較小的閾值(5 輪左右) 時, 聚類性能可以得到保證,F-measure值在0.6 附近. 當?shù)啍?shù)增多到15 之后,F-measure 值下降到0.3 以下, 模型基本喪失可用性.

5 總結(jié)

本文針對傳統(tǒng)的大數(shù)據(jù)聚類迭代算法, 基于組合性質(zhì)提出了一種差分可辨性隱私參數(shù)的迭代分配方法, 滿足了迭代輪數(shù)不固定情形下隱私參數(shù)的無窮分配, 也滿足了輪數(shù)固定時隱私參數(shù)的平均分配, 且最終迭代生成的模型滿足差分可辨性, 較好地體現(xiàn)了差分可辨性定義的先進性. 實驗結(jié)果表明, 差分可辨性隱私參數(shù)分配方法適用于k-means 聚類算法, 通過與差分隱私k-means 模型的對比, 可以看出本方法處理后的聚類模型也具有較好的分類效果.

差分可辨性能提供與差分隱私等價的隱私保護能力, 它在隱私保護應(yīng)用上同樣有很大價值. 相較于已有長足發(fā)展的差分隱私保護理論, 差分可辨性的研究目前仍有較大的空白和廣泛的前景.

目前對隱私參數(shù)ρ,m的選取大多依靠人為分析或?qū)嶒瀬頉Q定, 下一步仍需繼續(xù)研究具有科學(xué)性的方法, 針對不同維度、不同規(guī)模的數(shù)據(jù)集制定合理的隱私參數(shù). 除了聚類中的迭代加噪, 針對數(shù)據(jù)發(fā)布和其他機器學(xué)習(xí)等數(shù)據(jù)挖掘方法均有借助差分可辨性參數(shù)化隱私保護的研究前景, 可以探索差分可辨性的更多應(yīng)用.