李光輝,李俊鵬

(凱里學(xué)院理學(xué)院,貴州 凱里 556011)

1 引言

在許多實際問題中都會遇到求解二次型函數(shù)全局最值的問題,由于受到各種條件的限制,有時需要求解二次型函數(shù)在一些特殊約束下的最值.隨著科學(xué)技術(shù)的發(fā)展,人們所遇到的二次型優(yōu)化問題也越來越復(fù)雜.由于約束區(qū)域與函數(shù)向量都更為復(fù)雜,所以難以用統(tǒng)一的數(shù)學(xué)公式給出最優(yōu)化結(jié)果的顯示表達(dá).

約束域上二次型的優(yōu)化問題有著廣泛的應(yīng)用,例如,文獻(xiàn)[1-2]都使用算法搜索出在一些特殊區(qū)域上的二次型的全局最值.著名的Cramér-Rao不等式就是根據(jù)二次型下界所確定的,文獻(xiàn)[3]中第4章詳細(xì)討論了這一問題.文獻(xiàn)[4-5]介紹了關(guān)于二次型優(yōu)化在其他領(lǐng)域中的應(yīng)用.在特殊的約束條件中,單純形是一類常見的約束域,它是由q維空間中q個線性無關(guān)的點z1,z2,···,zq∈Rq所圍成的區(qū)域,將這一區(qū)域記為

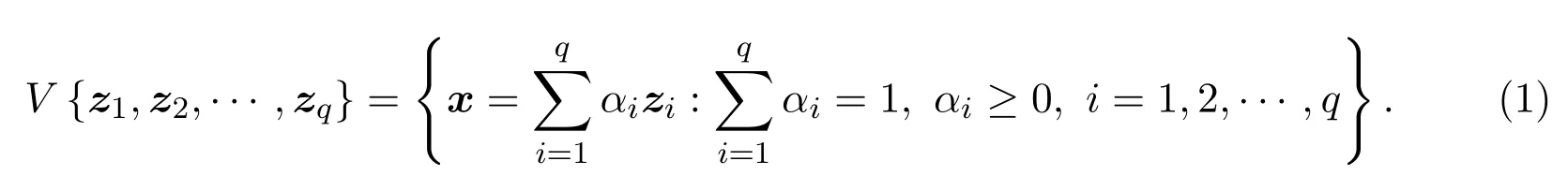
的最值問題.

在單純形約束域上求解二次型最值問題有著重要的背景.例如,在混料試驗設(shè)計中,為了判斷一個設(shè)計是否為最優(yōu),可以通過二次型優(yōu)化確定其方差函數(shù)在約束域上的最值,從而得到結(jié)論.關(guān)于混料設(shè)計中方差函數(shù)的優(yōu)化問題可以參見文獻(xiàn)[6-7].

鑒于此,本文研究在單純形域上二次型的優(yōu)化問題,構(gòu)造了在單純形域上搜索二次型最值的兩類算法.這兩類算法都能實現(xiàn)任意的函數(shù)向量所確定的二次型在單純形上的全局最值搜索.本文首先介紹單純形上二次型函數(shù)的定義;第2節(jié)構(gòu)造了一類適用于單純形上二次型優(yōu)化的Newton-Raphson算法;第3節(jié)討論了隨機搜索算法在搜索二次型函數(shù)最值的應(yīng)用;第4節(jié)通過模擬試驗說明這類算法的有效性;最后提出可進(jìn)一步研究的問題.

2 單純形上的Newton-Raphson算法

由于形如(1)式中的q維空間的單純形可以通過線性變換為標(biāo)準(zhǔn)單純形

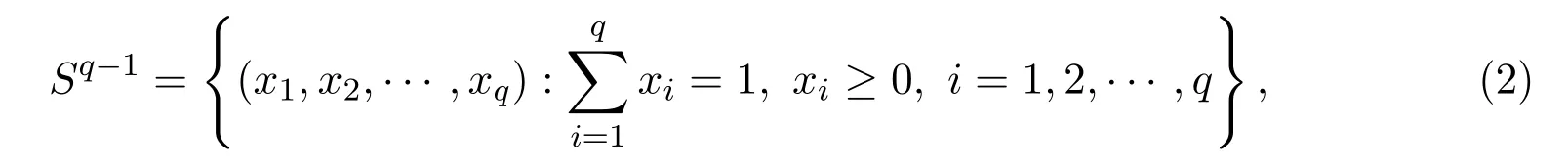
即對于任意的單純形都可以表示為

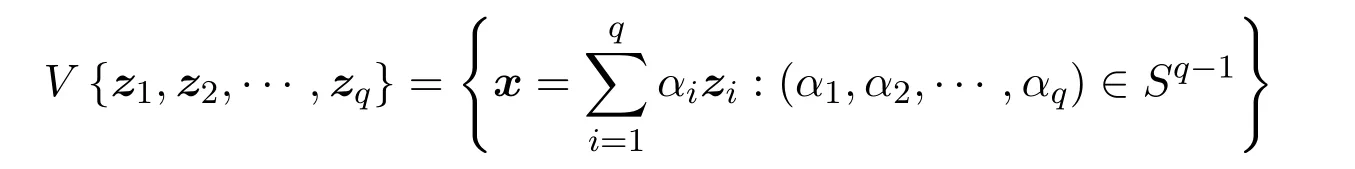
的形式.所以本文主要討論在Sq?1上的二次型優(yōu)化問題.設(shè)D是m階實對稱矩陣,需要優(yōu)化的模型為

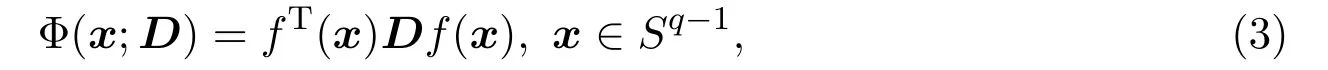
其中f(x)=(f1(x),f2(x),···,fm(x))T是已知的函數(shù)向量.

Newton-Raphson算法的基本思想是由某一點x(0)∈Sq?1的梯度方向確定最優(yōu)步長t,使得下一步迭代值x(1)=x(0)+t·?Φ(x(0);D)能使得 Φ(x;D)達(dá)到最大 (或最小),這里?Φ(x(0);D)表示x(0)點處的梯度向量.下面從梯度搜索方向與邊界點搜索兩方面討論.

為了使得x(0)點下一步搜索方向的向量必須與Sq?1共面,考慮將x(0)處的梯度投影在單純形上.因為二次型函數(shù)Φ(x;D)在任意一點x∈Sq?1的梯度向量為

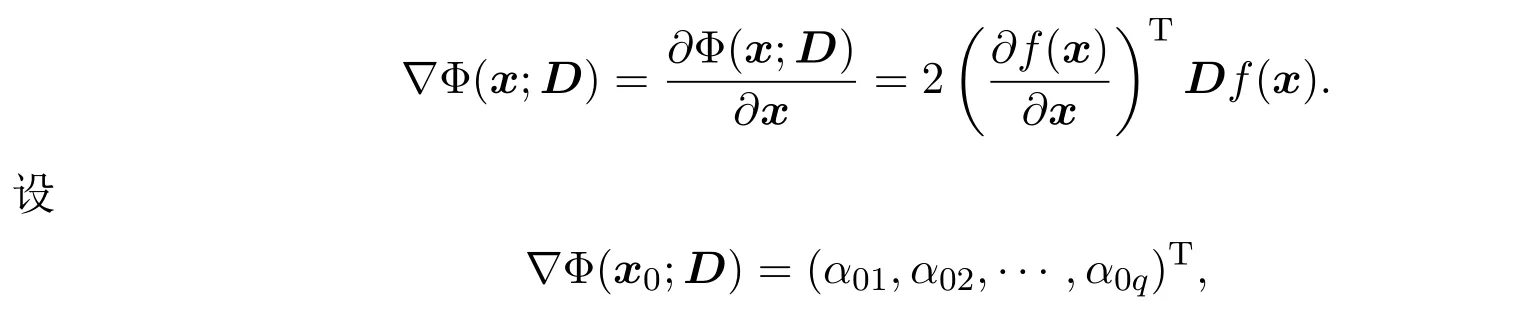
則過x0=(x01,x02,···,x0q)T且方向與?Φ(x0;D)一致的直線為

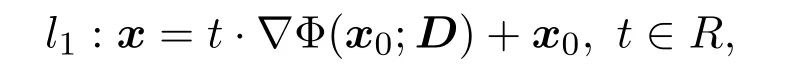
則直線l1上任意點x在Sq?1上的投影可表示為,其中

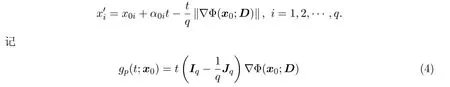
表示由x指向x′的向量,其中Iq為q階單位陣,,1q是元素全為1的q維列向量.

顯然對于任意的t∈R都有‖gp(t;x0)‖=0,即gp(t;x0)與單純形Sq?1是共面的,所以在x0處沿gp(t;x0)移動的點始終位于Sq?1上.gp(t;x0)就是x0點的梯度向量在單純形上的投影,通過控制參數(shù)t可以確定下一步迭代的最優(yōu)解,即下一步迭代點與x0之間存在形如x=x0+gp(t;x0)的關(guān)系.下面討論邊界點搜索的問題.

由于當(dāng)x0點位于Sq?1的邊界時,下一步迭代的最優(yōu)解往往會超出Sq?1.為了更好地實現(xiàn)在邊界上的搜索,設(shè)立一個松弛變量ε>0,令

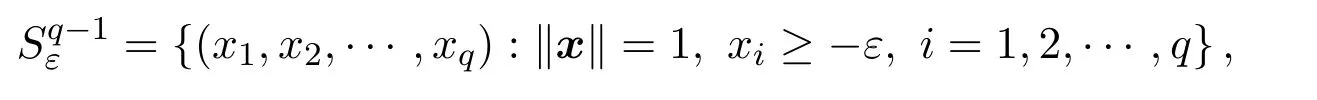
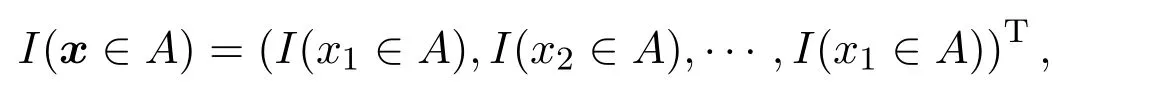
其中I(·)為示性函數(shù).記I+=I(x>1),I?=I(x<0).對于任意點,如果x中所有大于 0的分量為xi1,xi2,···,xik,令,j=1,2,···,k.定義變換系數(shù)

令γ=(γ1,γ2,···,γq)T,定義在邊界上搜索的函數(shù)為

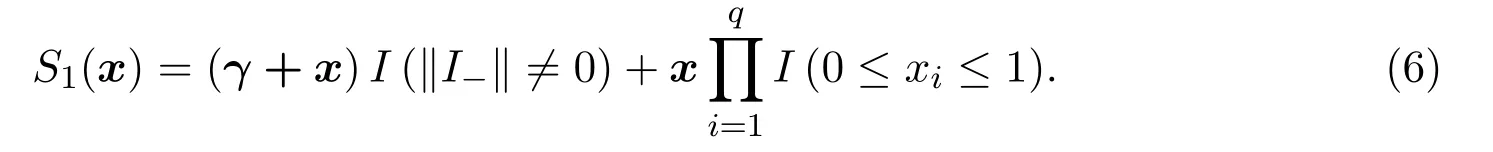
稱(6)式中的S1(x)為I型貼邊函數(shù),其功能主要是將超出Sq?1的點沿梯度投影在邊界上.由于二次型函數(shù)(3)在Sq?1上往往會呈現(xiàn)出多峰的形態(tài),所以為了搜索出全局最值點,可以考慮同時投入若干個初值點,同時進(jìn)行搜索,每個點經(jīng)過形如(4)式的迭代稱為一步搜索,將所有點都經(jīng)過一步搜索的過程稱為一輪搜索.以搜索二次型函數(shù)最大值為例,將搜索過程整理為以下算法.

算法1: 單純形上的Newton-Raphson算法輸入:迭代初值x(0)1,x(0)2,···,x(0)n 以及松弛變量 ε>0 1: For j=1 to N 2: For i=1 to n 3: 確定常數(shù)a(j)i≥0使得x(j)i+gp(t;x(j)i)∈Sq?1ε成立4: t(j)i?opt=arg max 0≤t≤a(j)i{Φ(x(j)i +gp(t;x(j)i))}5: x(j+1)i =S1(x(j)i +gp(t(j)i?opt;x(j)i))6: End for 7: End for

3 單純形上的隨機搜索算法

根據(jù)文獻(xiàn)[8]的思想,首先構(gòu)造單純形區(qū)域上的均勻分布的隨機點集,然后將其映射到一個子區(qū)域,從中選取最優(yōu)點作為迭代的下一步,以此類推,直到所有點都固定.以下從隨機點的產(chǎn)生與迭代過程的進(jìn)行兩方面進(jìn)行討論.

為了使得搜索效率更高,本文采用單純形格點集混合均勻分布的隨機點集作為備選點集.根據(jù)文獻(xiàn)[9]中所介紹的在單純形上生成均勻分布的隨機點集的方法,可以令矩陣

以搜索二次型函數(shù)最大值為例,將以上搜索過程整理為以下算法.

算法2: 單純形上的隨機搜索算法輸入:迭代初值x(0)1,x(0)2,···,x(0)n,擬分量變換參數(shù)序列 λ(M)<···<λ(2)<λ(1),松弛變量ε>0,固定格點集T2=L(q,m).1: For j=1 to M 2: For i=1 to n 3: 產(chǎn)生服從單純形上均勻分布的隨機點集,并按行排列為T(j)1 ～ U(Sq?1)4: T(j+1)C =C([T(j)T 1 ,TT2]T,x(j)i ,λ(j))5: T(j+1)=■■ x(j)i T(j+1)C■■,并記T(j+1)為T(j+1)中各行為點構(gòu)成的集合6: x(j+1)i =argmax x∈T(j+1)Φ(x)7: End for 8: End for

經(jīng)過M輪搜索后,會駐留在Φ(x;D)的各個子區(qū)域的最值處.

4 模擬實例

本節(jié)使用兩種算法搜索三分量二次型函數(shù) Φ(x)=fT(x)Mf(x)?6在S3?1上的最大值,其中f(x)=(x1,x2,x3,x1x2,x1x3,x2x3)T,使用 3分量 2階格子點集L{3,2}={z1,z2,···,z6}.并令

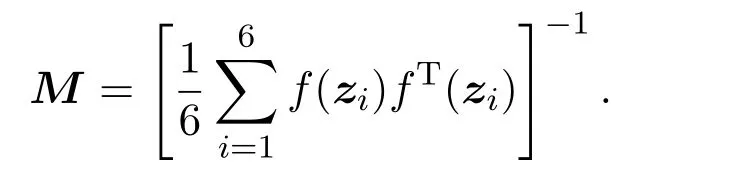
Φ(x)的曲面圖如圖1(a)所示.

使用兩種算法搜索Φ(x)在S3?1上的最大值.首先在S3?1中產(chǎn)生100個均勻分布的隨機點作為初值.使用算法1,取松弛變量ε=0.1,經(jīng)過 35輪迭代即可得到最優(yōu)解.

圖1 (a)二次型曲面圖;(b)算法1搜索過程Φ(x)迭代值;(c)算法2搜索過程Φ(x)迭代值

不論使用哪種算法,最終搜索得到的最值點都相同,100個初值最終都重合到7個點處,分別是S3?1上的3個頂點z1=(1,0,0),z2=(0,1,0),z3=(0,0,1)和三個棱中點z4=(0.5,0.5,0),z5=(0.5,0,0.5),z6=(0,0.5,0.5).從圖1(a)中也可見,z0是Φ(x)函數(shù)的一個極大值點.算法1之所以會確定該點是因為搜索過程中,在該點處的梯度向量始終為0,所以后續(xù)的迭代都無法進(jìn)行.算法2則是因為該點是極大值點,在以該點為中心的一個子單純形領(lǐng)域內(nèi),再無法產(chǎn)生使得函數(shù)值更大的備選點.所以,這兩類算法不僅可以搜索得到二次型函數(shù)在單純形域上的全局最值,還可以搜索出各個極值點.

5 討論

通過實例可以驗證這兩種算法的有效性,并且這類算法對于單純形域上的其他函數(shù)也同樣適用.一般的,如果Φ(x)在任一點x∈Sq?1處的梯度都存在,那么使用算法1的收斂速度會更快.而如果Φ(x)形式復(fù)雜,梯度向量沒有顯示表達(dá),則使用算法2更為穩(wěn)健.總體而言,算法2易于實施,不用關(guān)心迭代點的搜索方向,只考慮備選點集分布的均勻性即可.

此外,如果搜索區(qū)域是單純形內(nèi)部的一個子區(qū)域,特別當(dāng)約束條件過多,區(qū)域形式較為復(fù)雜的時候,如何在邊界上執(zhí)行搜索過程就是一個難題,并且對于初值的選取十分敏感.為此,可以考慮在約束區(qū)域內(nèi)產(chǎn)生均勻足夠高階的格子點集,并且使得這個格子點集合能夠包含這一區(qū)域各個頂點與棱中點,由此可以確定出一組較好的搜索初值.

這兩類算法在單純形上的二次型函數(shù)的搜索是十分有效的,如果約束過多,函數(shù)復(fù)雜,使用算法2來搜索函數(shù)最值是比較有效的方法.