Zakharov VE

1 正則變量

考慮均勻重力場中無限深理想流體的有勢流動, 選擇如下坐標系:xy平面與未受擾動的流體表面重合, 而z軸則沿著遠離該平面的方向. 在下文中, 所有矢量均為xy平面中的二維矢量.

記η(r,t)為 流體表面的波形函數(shù),Φ(r,z,t)為速度勢函數(shù). 流體的流動可用Laplace方程描述

在自由面上滿足兩個條件

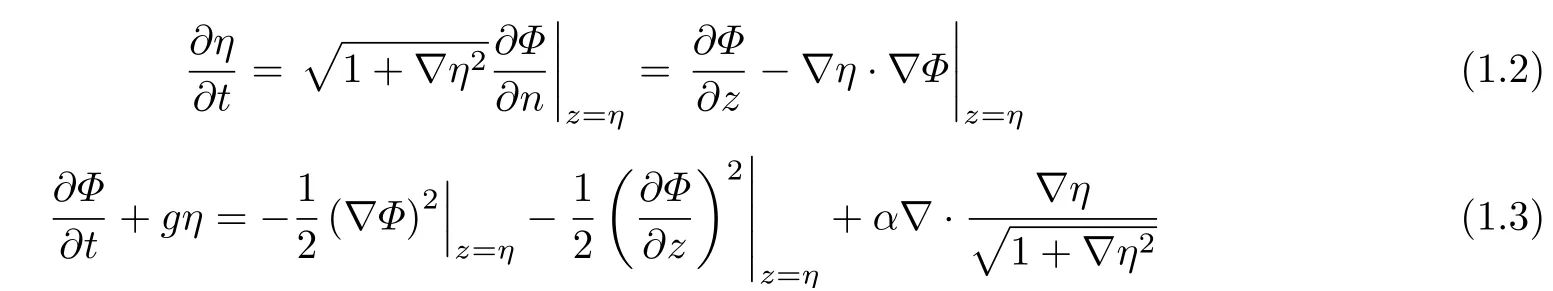
以及在無窮遠處有條件

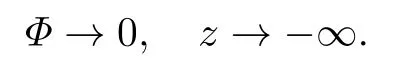
式中g為重力加速度,α為表面張力系數(shù).

方程(1.1) ~ (1.3)滿足流體的總能量守恒

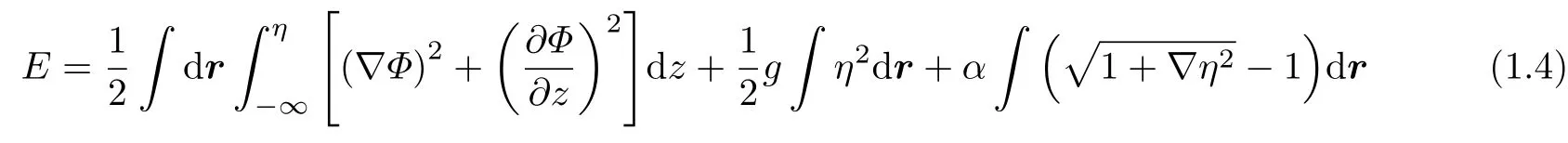
式中, 等號右邊第一項為動能, 第二項為重力勢能, 第三項為表面張力勢能. 引入物理量Ψ(r,t)=Φ(z=η(r,t),r,t). 由于拉普拉斯方程的邊值問題有唯一解, 因此只需要兩個物理量η與Ψ即可以確定流體的流動. 考慮到

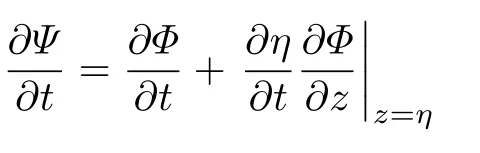
可得到

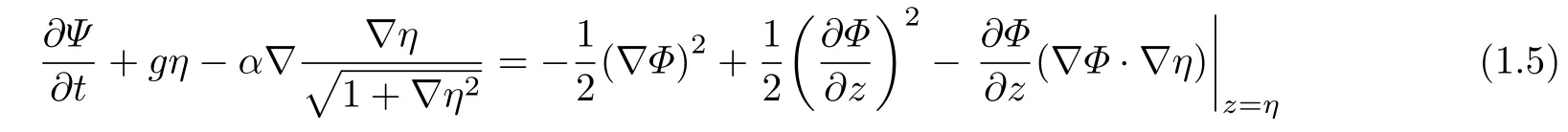
方程(1.2)和(1.5), 連同拉普拉斯方程, 等價于方程(1.1) ~ (1.3). 可以證明方程(1.1)和(1.5)可以寫

式中E是能 量, 符號表示變分導數(shù).

首先考慮關于Ψ的變分. 顯然, 勢能對Ψ的變分為0. 利用格林公式, 動能可改寫成

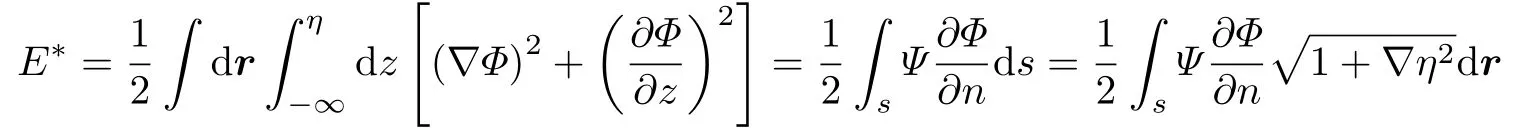
式中 ds是 面積微元, 可以利用拉普拉斯方程邊值問題的格林函數(shù), 將法向?qū)?shù)?Φ/?n與Ψ聯(lián)系起來

式中s和s1是 表面上的點. 格林函數(shù)G是 對稱的, 即動能的變分有兩項

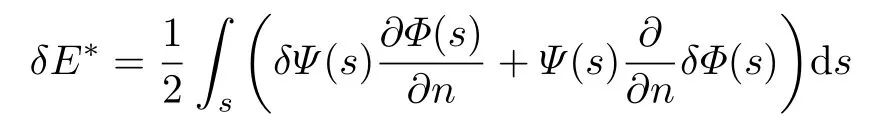
根據(jù)式(1.7)和格林函數(shù)的對稱性, 可以發(fā)現(xiàn)這兩項是相等的

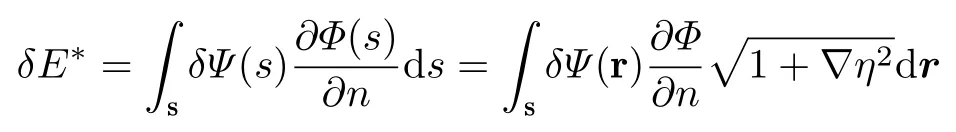
由此立即得到式(1.2).

現(xiàn)在考慮對η的變分 (這個簡單的證明由Garipov R M給出) .

對勢能做變分立即給出式(1.5)①譯者注: 原文為式(2.5), 應為式(1.5).的左側(cè)項. 動能的變分給出

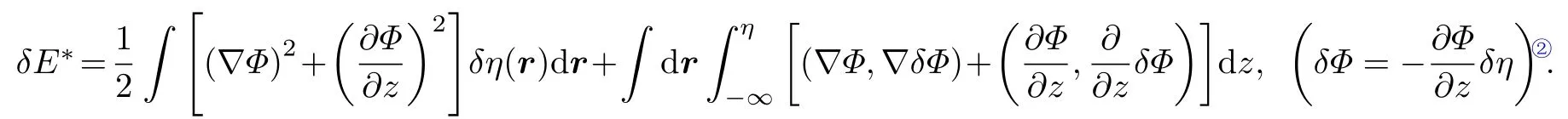
式中,δΦ為 邊界的改變而引起的變分. 由于Φ滿足拉普拉斯方程, 可以對第二個積分使用格林定理

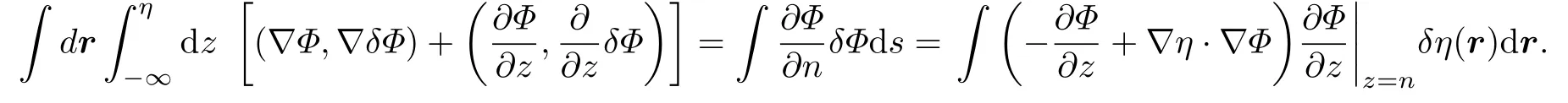
最后我們有

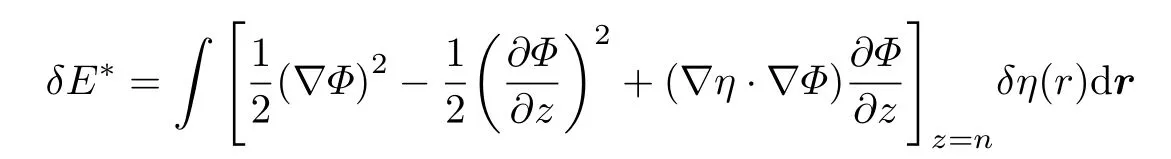
于是得到式(1.5).

因此, 方程(1.2)和方程(1.5)是哈密頓方程,Ψ和η為 正則變量, 其中Ψ為廣義坐標, 而η為廣義動量. 流體的能量E為哈密頓量.

為了使方程(1.1)和(1.5)封閉, 必須求解拉普拉斯方程的邊值問題, 找到該問題關于η的冪級數(shù)形式的解. 如果對變量x和y作傅里葉變換

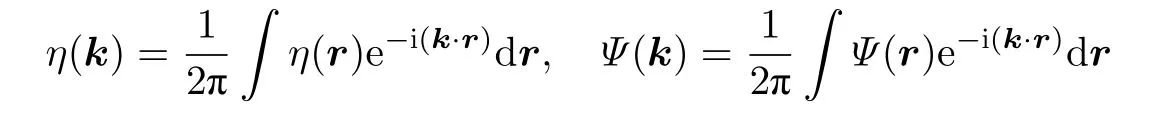
將得到更為合適的級數(shù)形式.

省略細節(jié), 立即給出展開的結果 (展到二階項)

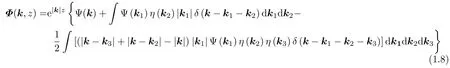
式中δ為狄拉克函數(shù).

如果線性化式(1.2)和式(1.5)并僅考慮式(1.8)中的第一項, 將獲得流體的小振幅表面波理論, 用于描述具備如下色散關系的波傳播

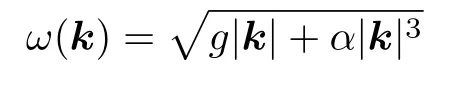
通過下面的方程實現(xiàn)到復變量的變換

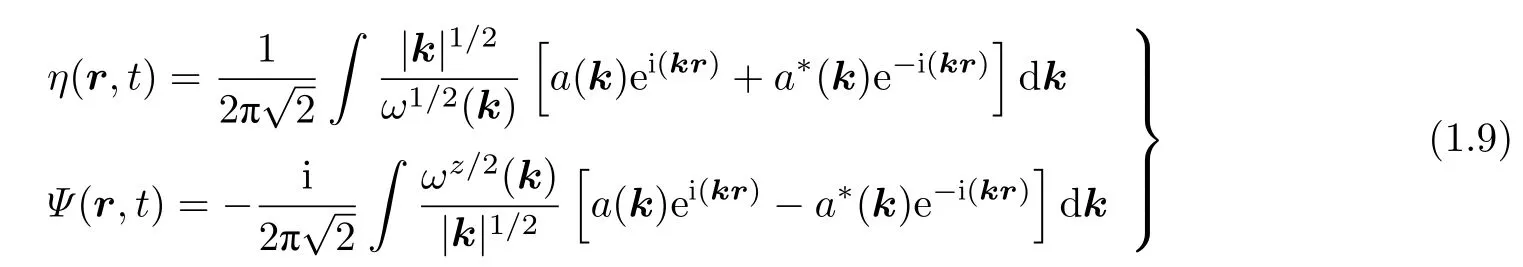
于是

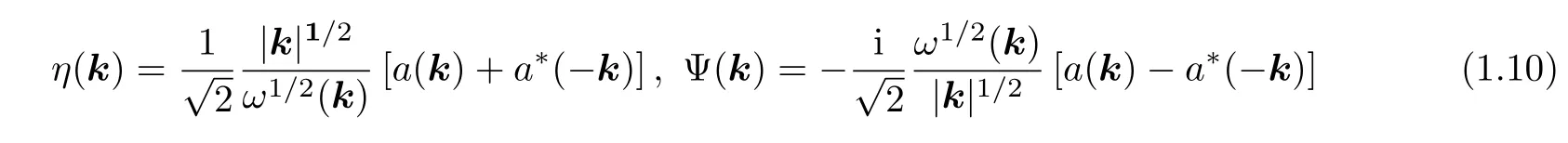
變換(1.9)可視為到變量 ia?(k)和a?(k)的正則變換 (帶有復系數(shù)) ; 則哈密頓方程(1.6)變?yōu)閱蝹€方程

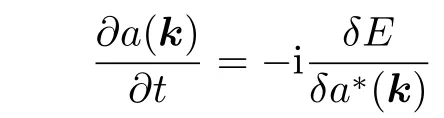
利用方程(1.4), (1.8)和(1.10), 可以將能量表示為關于a(k)和a?(k)的級數(shù)形式

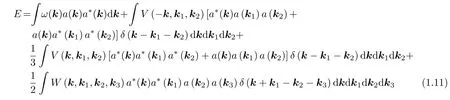
其中

式中還有關于其他的四階項, 與α?ααα和αααα形式的乘積及其共軛成正比. 如第3節(jié)所示, 由于這些項的貢獻很小, 因此將會被忽略掉.

注意到函數(shù)V和W滿足以下方程

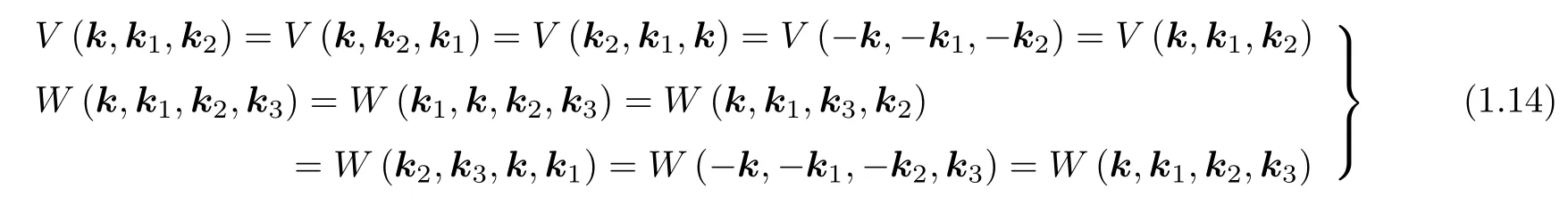
因此關于a(k)的方程具有如下形式

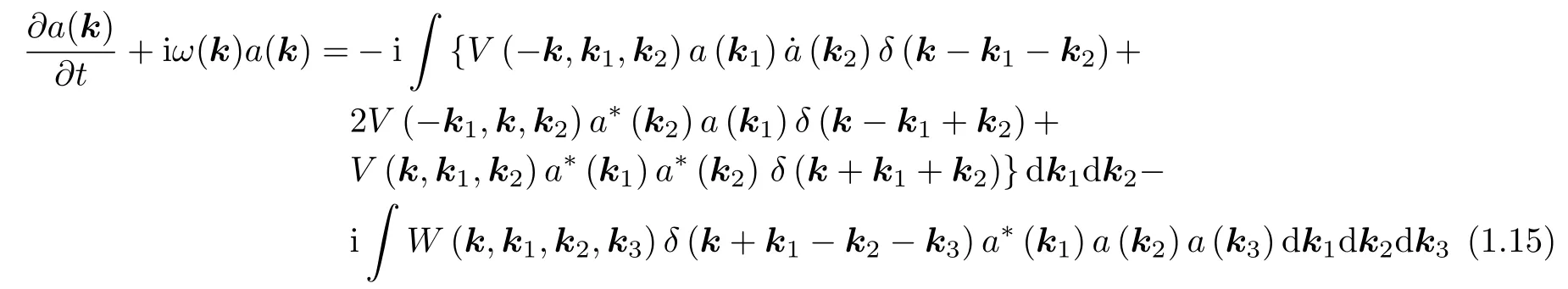
從 式(1.15)中可以看出,a(k)是小振幅問題的正態(tài)變量.

2 簡化方程

方程(1.15)是一個適用于弱非線性的近似方程. 粗略地講, 該方程適用于a/λ?1的情況, 其中a為波的特征振幅,λ為特征波長. 在這種近似中, 可以對方程(1.12)進行簡化. 為此, 將a(k)寫為

顯然, 哈密頓量(1.11)中忽略的那些項對式(2.4)沒有貢獻.

在使用式(2.3)時, 必須假設f?A. 為使這一條件成立, 式(2.2)和式(2.4)中的分母不為 0是必須的. 當方程

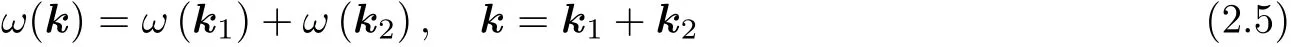
有解時, 分母為0.

如果ω(k)是單調(diào)函數(shù), 注意到方程(2.5)有解的一個充分條件是

其中k和k1共 線. 事實上, 如果式(2.6)成立, 可以通過把垂直于k的k1分 量添加到k1中, 放大方程(2.6)的右側(cè)從而將其轉(zhuǎn)化為等式. 另一方面, 如果與式(2.6)相反的不等式成立, 則該條件即為方程(2.5)無解的充分條件. 對于重力波, 有色散關系

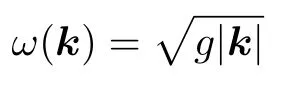
為了進一步簡化方程, 引入變量ξ=x?ct(這相當于轉(zhuǎn)換到一個以群速度移動的坐標系); 假設解僅依賴于t和z=ξcosα+ysinα; 于是得到

方程(2.3)具有精確解

式中b0為 任意常數(shù). 對于變量η和Ψ, 解式(2.10)具有如下形式

通過計算可以得到

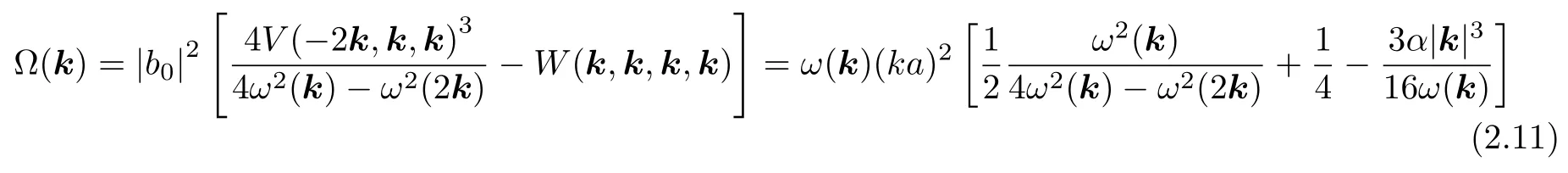
在極限情況下, 對于k值較小時有?(k)=1/2(ka)2ω(k), 這與Stokes在1847年獲得的表達式一致.因此, 解式(2.9)近似為一個有限振幅的周期波.

當

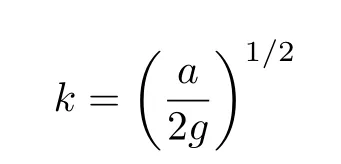
頻率的偏移變?yōu)闊o窮大; 對于k值較大時, 頻率偏移為負值.

在極限情形k→∞下, 可得

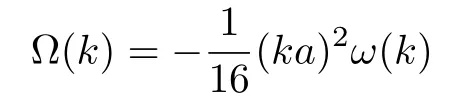
3 有限振幅波的穩(wěn)定性

考慮在定常周期波背景下小擾動的發(fā)展. 尋找以下形式的a(k)

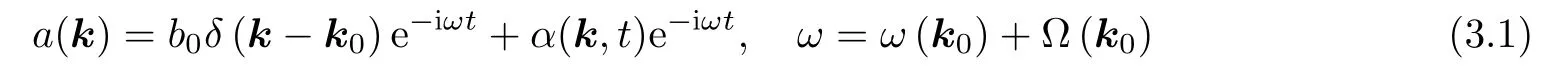
假設α在如下不等式中足夠小

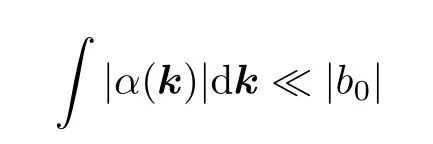
現(xiàn)將方程(1.15)對α(k)線性化. 為此僅考慮方程右側(cè)隨時間緩慢變化的項. 可得

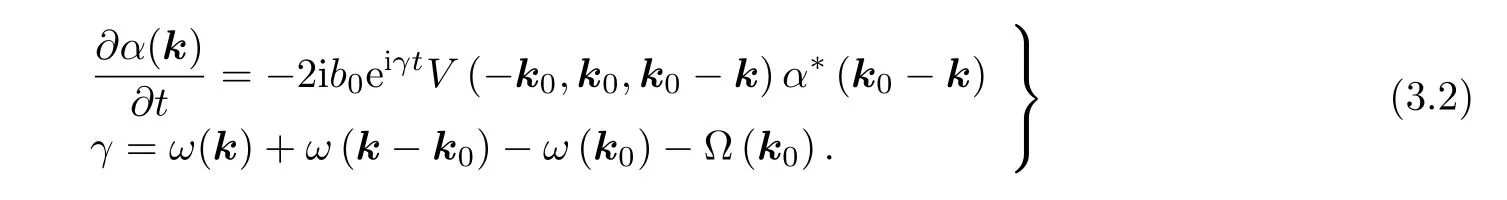
從式(3.2)中消去α?(k0?k), 可得

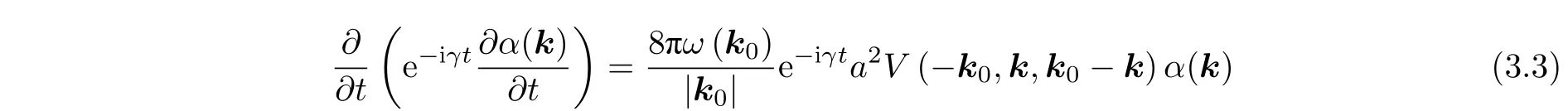
方程(3.3)有以下形式的解

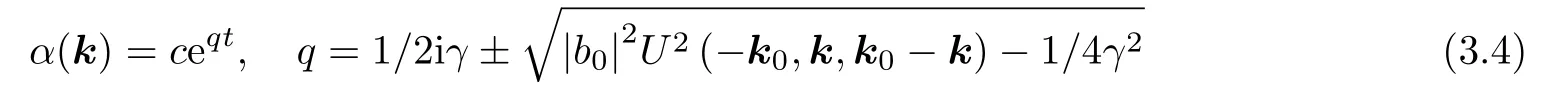
如果根號內(nèi)的表達式為正, 則將會產(chǎn)生不穩(wěn)定. 為了使對于任意小的b0系統(tǒng)都會產(chǎn)生不穩(wěn)定,方程γ=0應 當有一個解. 如果忽略了方程中的小量?(k0), 可得到方程組(2.5). 如第二節(jié)中建立的那樣, 該系統(tǒng)對于毛細波問題可解; 因此, 該類型的不穩(wěn)定性會在毛細波中產(chǎn)生. 不穩(wěn)定的波矢量集中在面ω(k)=ω(k1)+ω(k?k1)附近的薄層中, 其厚度與振幅成比例. 不穩(wěn)定性的最大增量的量階為Req～(ka)ω(k).

對重力波而言, 這種類型的不穩(wěn)定性是不存在的. 但是重力波可能會出現(xiàn)較為緩慢的不穩(wěn)定.將具有如下形式的A(k)代入方程(2.3)

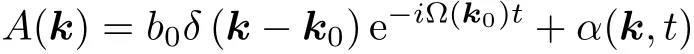
如果對α(k)線性化, 有

該式可以簡化為式(3.2)形式的方程; 該方程存在一個與 exp(qt)成比例的解, 其中q為

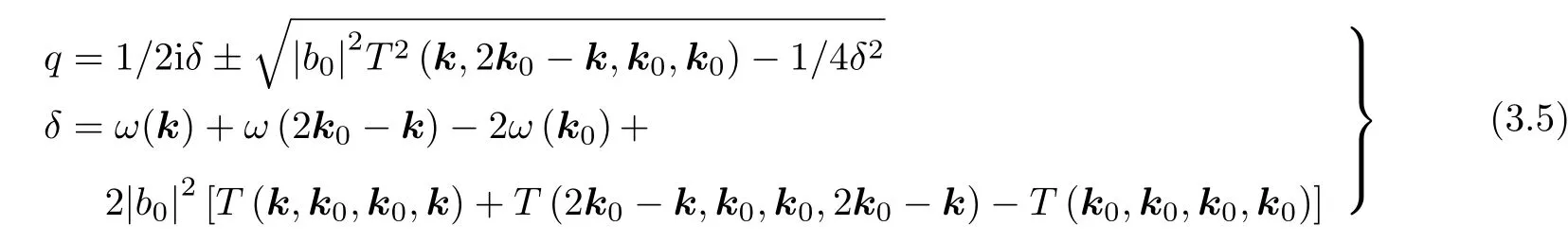
考慮第一種情況

與b2成 比例的項可從式(3.5)中舍棄. 對于任意小振幅, 存在不穩(wěn)定性的條件是δ=0, 該條件等價于下面方程解的存在性條件

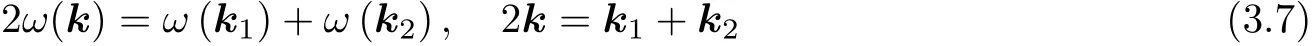
顯然, 這些方程有解的一個充分條件為

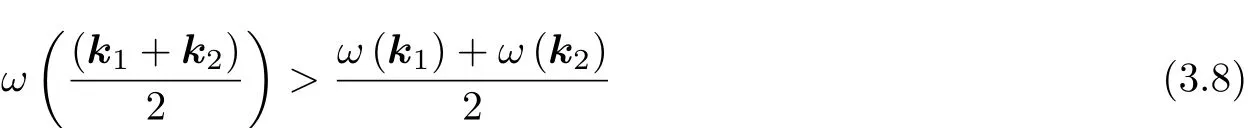
其中式中向量k1與k2平 行. 不等式(3.8)要求ω(k)是上凸的. 對于重力波

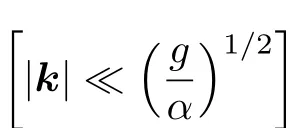
該不等式必然成立.

相反地, 對于毛細波, 反向不等式成立, 表明該類型的不穩(wěn)定性是不可能的.

方程(3.7)在k空間中定義了一個面. 不穩(wěn)定的波矢位于該面附近, 其厚與b2成比例. 重力波不穩(wěn)定性的最大增長率的量階為

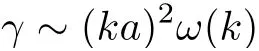
存在與n的守恒律相對應的高階不穩(wěn)定性

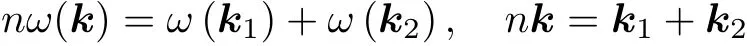
這種不穩(wěn)定性增長率的量階為γ～(ka)nω(k).

以上這些不穩(wěn)定性都可以稱為破壞性的.

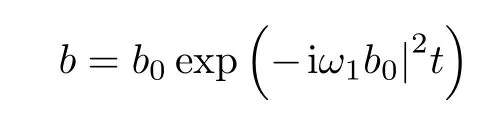
對應于一個有限的振幅.

尋找以下形式的解

對于ω有

從式(3.9)可以看出, 如果ωλ<0, 則可能產(chǎn)生不穩(wěn)定性, 但是只有足夠小的波矢才會激發(fā)不穩(wěn)定

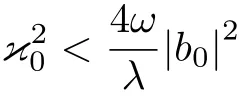
考慮表面波在不同波數(shù)下的情況.

(1) 波數(shù)區(qū)間

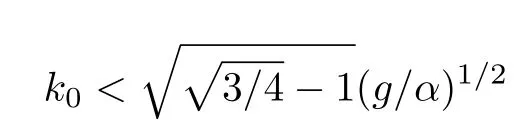
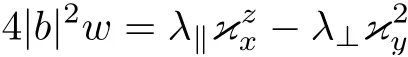
及其漸近線之間.

(2) 波數(shù)區(qū)間

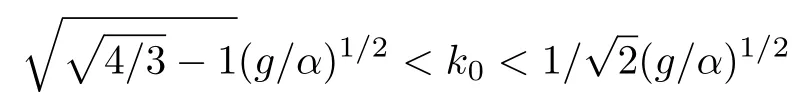
其中w>0,λ⊥>0,λ∥>0, 此時不穩(wěn)定性一般不可能產(chǎn)生.

(3) 毛細波區(qū)間

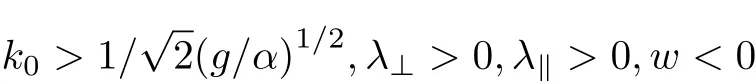
不穩(wěn)定的區(qū)域為橢圓內(nèi)部

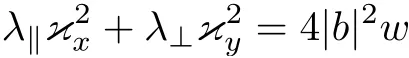
可以對方程(2.9)作變量變換

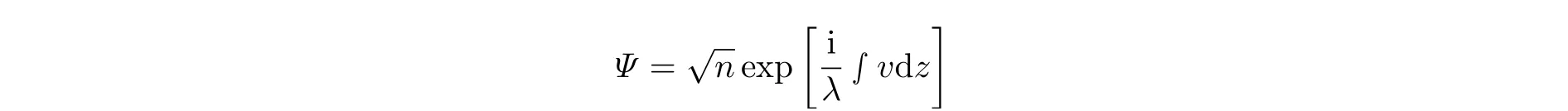
方程(2.9)可化為

這些方程與壓力和密度具有絕熱關系的氣體動力學方程

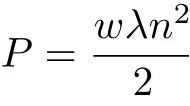
類似, 它們的區(qū)別在于毛細波包含了對z的三階導數(shù)項. 如果考慮特征尺度為L的充分大尺度的運動, 則對于

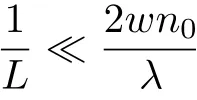
三階導數(shù)項即可被忽略. 對于正壓力wλ>0 , 方程(3.10)描述了波速為的聲波. 對于負壓力, 此時聲波的速度為虛數(shù), 這意味著初始擾動會呈指數(shù)增長

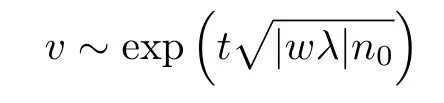
由此, 得到了負壓型不穩(wěn)定性的情況.

注意到如果在式(3.6)中令k→k0, 則式(3.9)可從負壓不穩(wěn)定性的增量得到. 因此, 負壓不穩(wěn)定性是重力波緩慢破壞不穩(wěn)定性的極限情況.

感謝與Ovsyannikov L V和Sagdeev R Z收獲頗豐的討論.