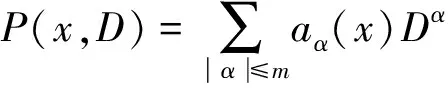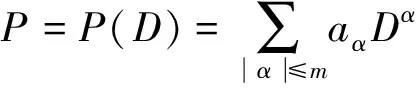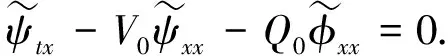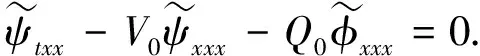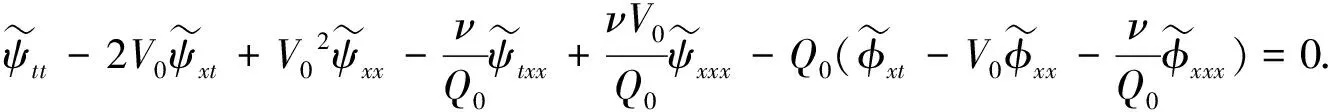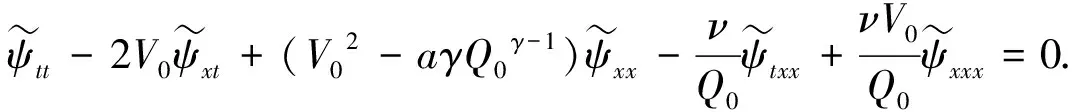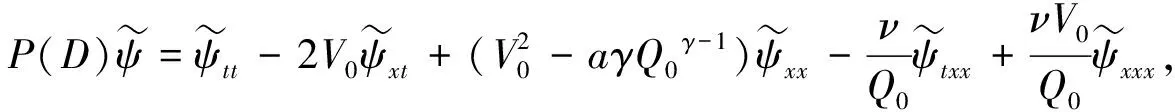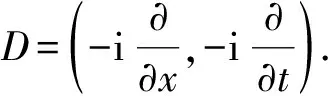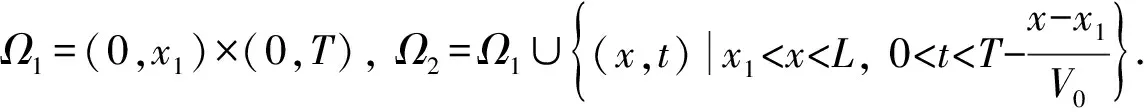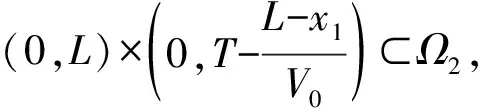一維線性化可壓縮Navier-Stokes方程組的近似能控性
杜潤梅, 呂曉娜
(長春工業(yè)大學(xué) 數(shù)學(xué)與統(tǒng)計學(xué)院, 長春 130012)
0 引 言
Navier-Stokes方程組是流體力學(xué)方程中描述黏性牛頓流體的方程. 一維的可壓縮等熵Navier-Stokes方程組為
其中ρ(x,t)表示流體的密度,v(x,t)表示流體的速度, 正數(shù)ν表示流體的黏性,f表示質(zhì)量源,g表示外力, 壓力p滿足p(ρ)=aργ,a>0,γ≥1.
目前, 關(guān)于可壓縮Navier-Stokes方程組的性質(zhì)研究已取得了很多成果[1-8].其中, 文獻[5-6]研究了線性化可壓縮Navier-Stokes方程組的一些可控性結(jié)果.本文考慮在常數(shù)穩(wěn)態(tài)(Q0,V0)附近線性化的Navier-Stokes方程, 其中Q0>0,V0>0.先考慮如下初邊值問題:
其中Q0>0,V0>0, (x,t)∈QT=(0,L)×(0,T),ω=(0,x1), 0 類似于文獻[5]中定理2.3和文獻[6]中命題2.1, 由半群理論可得系統(tǒng)(1)-(4)的適定性: 命題1對任意(σ0,u0)∈L2(0,L)×L2(0,L), 系統(tǒng)(1)-(4)存在唯一弱解(σ,u)∈X, 滿足ut∈L2(0,T;H-1(0,L)), 其中 X=C([0,T];L2(0,L))×[L2(0,T;H01(0,L))∩C([0,T];L2(0,L))]. 令Z=L2(0,L)×L2(0,L), 在Z上定義其內(nèi)積和范數(shù)分別為 在Z上, 方程組(1)-(4)的對偶問題為 下面給出對偶問題(9)-(12)的唯一延拓性: (13) 則有 由定理1, 可得對偶問題(5)-(8)的唯一延拓性: 由對偶問題(5)-(8)的唯一延拓性, 可得(1)-(4)的近似能控性: ‖(σ(x,T),u(x,T))-(σd(x),ud(x))‖L2(0,L)×L2(0,L)≤ε. 下面證明對偶問題(9)-(12)的唯一延拓性. 定義1設(shè)曲面S?N是C1的, 且曲面S在點x處的法向量為ξ.如果Pm(x,ξ)=0, 則稱曲面S在點x處對于P(x,D)是特征的.如果曲面S在所有點處都是特征的, 則稱曲面S為P(x,D)的特征曲面. 1) 設(shè)在分布意義下,Θ∈D′(Ω2)滿足P(D)Θ=0且Θ(x)在Ω1上為0, 則Θ(x)在Ω2上也為0; 2) 每個與Ω2相交的P(D)的特征超平面一定與Ω1相交. (14) (15) 對式(15)中x求導(dǎo), 得 (16) 由式(14)~(16), 得 即 (17) 把式(10)代入式(17), 得 (18) 定義算子 (19) 引理2P(D)的特征超平面是t=C1和t+x/V0=C2, 其中C1和C2都是常數(shù). 證明: 假設(shè)Π={(x,t):ξx+ηt=C}是P(D)具有法向量(ξ,η)≠(0,0)的特征超平面.根據(jù)定義1, 可知 因此ξ=0或η=V0ξ.從而特征超平面Π的法向量是(0,1)和(1/V0,1).于是P(D)的特征超平面是t=C1和t+x/V0=C2.證畢. 下面證明定理1. 證畢.1 線性化系統(tǒng)的近似能控性
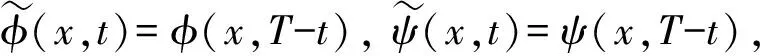
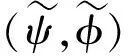
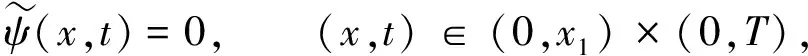
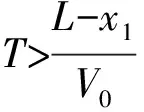
2 定理1的證明