Zhi-Da Bai(白志達) Zhen-Xiang Zhong(鐘振祥) Zong-Chao Yan(嚴宗朝) and Ting-Yun Shi(史庭云)

1State Key Laboratory of Magnetic Resonance and Atomic and Molecular Physics,Wuhan Institute of Physics and Mathematics,Innovation Academy for Precision Measurement Science and Technology,Chinese Academy of Sciences,Wuhan 430071,China

2University of Chinese Academy of Sciences,Beijing 100049,China

3Department of Physics,University of New Brunswick,Fredericton,New Brunswick,E3B 5A3,Canada

Keywords: exotic atom,pionic helium,fine structure,hyperfine structure

1.Introduction

The pionic heliumπHe+is a quasi-bound three-body atomic system consisting of a helium nucleus, an electron in the 1s orbital, and aπ-meson occupying a Rydberg state of large principal quantum numbern～16 and orbital angular momentum?～n-1.These states ofπHe+are predicted to have a nanosecond-scale lifetime,[1]allowing for laser spectroscopy measurements.Recently, the transition(n,?) = (17,16)→(17,15) inπ4He+was detected experimentally for the first time at Paul Scherrer Institute (PSI).[2]The next phase work of spectroscopy measurements at PSI is to push the measurement accuracy to the level of parts per billion (ppb),[3,4]so that a much improved value ofπ-mass at ppb level could be derived in combination with high-precision quantum electrodynamic(QED)calculations.At this level of precision, knowledge about fine and hyperfine structures (forπ3He+) is essential for correctly determining the “central”spin-averaged transition frequency.So far, the study of the fine structure ofπ4He+andπ3He+has been done in Ref.[1],but the hyperfine structure ofπ3He+has not yet been reported.The purpose of this paper is to conduct a comprehensive study of fine and hyperfine structures of some metastable states inπ3,4He+.

The structure of this paper is as follows.Section 2 describes the variational calculations of the wave functions under the closed-channel approximation.[5]Section 3 presents the theory of fine and hyperfine structures and numerical calculations of the associated coupling coefficients.Finally, a summary is given in Section 4.Atomic units (e= ˉh=me=1) are used throughout, unless otherwise stated.In order to facilitate a comparison with the previous calculations in Ref.[1], the same masses ofπ-and3,4He nuclei are used,mπ= 273.1320me,[6,7]mh= 5495.8852754me, andmα=7294.2995361me,[7]without considering their uncertainties.

2.Variational wave functions

After removing the center of mass motion, the nonrelativistic Hamiltonian of a three-body Coulombic system can be written in the form of

Here the helium nucleus of massm0is taken as the zeroth particle sitting at the origin of the reference frame,indices 1 and 2 are designated, respectively, for the electron and pionπ-,μ1andμ2are their reduced masses with respect to the helium nucleus,z0,z1, andz2are the charges of the three particles,andr12=r1-r2.

Since any pion-excited states inπHe+are embedded in the singly excited electron continuum, these states are quasistable resonance states against Auger decay.Here we apply the Feshbach projection formalism[9,10]to seek the closedchannel quasi-bound solutions ofH0, using the variational principle.[11]The Rayleigh-Schr¨odinger variational principle can be extended to the excited states by Hylleraas-Undheim-McDonald theorem.[12]We introduce a pair of projection operatorsPandQ,which satisfy

wherePandQare the usual open and closed channel operators, respectively.OnlyL2-type wave functions are used to diagonalize the HamiltoniansQH0Qand no open channel components are included.[13]The resonance eigenvalues deduced in above truncated diagonalization procedure would be upper bounds to the eigenvalues ofQH0Q.[13]In particular,the eigenvalue problem ofQH0Q,

The uncertainty is taken to be the difference betweenE0(∞)andE0(ΩMax).Our calculated energy agrees with the value of Horiet al.[1]The convergence study for the other energy levels is similar to the(17,16)state.It should be noted that the precision of closed-channel approximation within Feshbach formalism is limited by the width of the metastable states.[11]Thus, for some short-lived state such as (15,14), the present results have less converged digits.The accuracy of expectation values of other operators is limited by the precision of nonrelativistic wave functions.

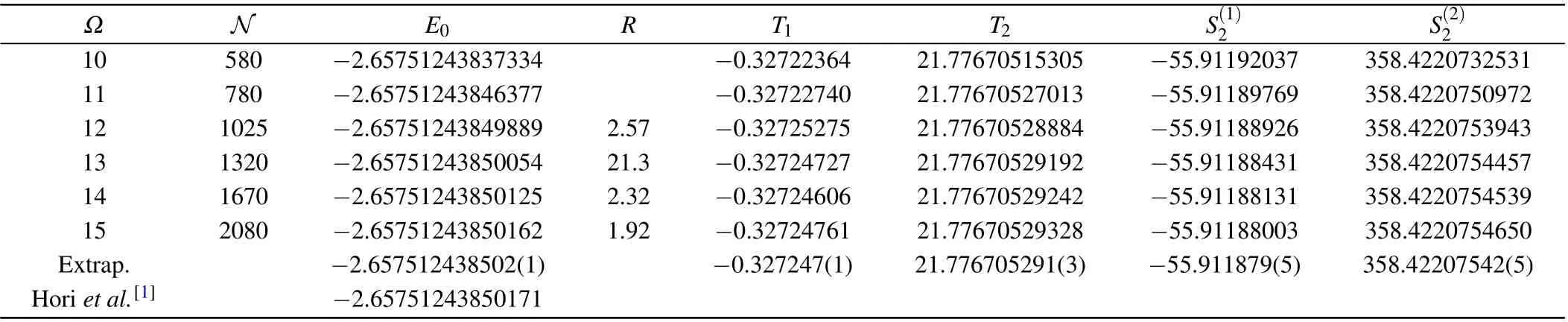
Table 1.Convergence study of the energy eigenvalue and some reduced matrix elements for the state(17,16)of π4He+.

3.Fine and hyperfine structures

The spin dependent part of the Breit-Pauli Hamiltonian[20,21]is responsible for the leading-order fine and hyperfine structures.For a pionic helium where the spin of pion is zero,the spin-orbital interaction is

and the spin-spin one is

wherep0=-p1-p2,s0is the helion spin, ands1is the electron spin.In the above,g0=gh(mh/mp) =-12.736614736(50)anda0=g0/4-1=-4.184153684(12),withghbeing the helion’sg-factor,mh/mpthe heloinproton mass ratio, anda0the helion’s magnetic moment anomaly.[7]Similarly, the electrong-factor isg1=ge=-2.00231930436153(53)and the magnetic moment anomaly isa1=ae=1.15965218076(27)×10-3.[7]The corrections due to the finite nuclear size effect is negligible at the current accuracy.[8]

Table 2.Expectation values of various operators for π4He+.

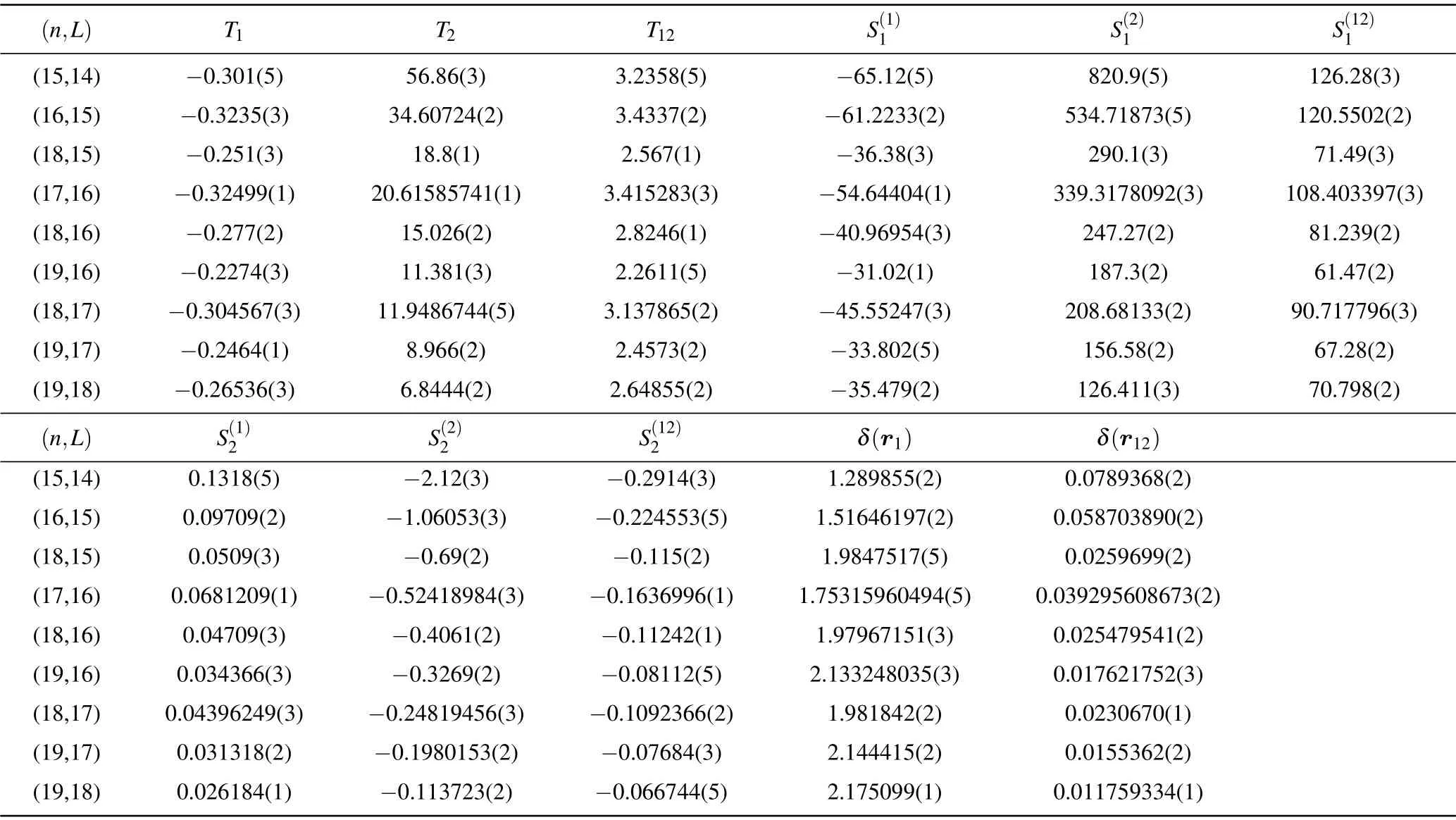
Table 3.Expectation values of various operators for π3He+.

Since the4He nucleus also has zero spin, the effective Hamiltonian of the fine-structure ofπ4He+is

where the fine-structure coefficientε1can be calculated by integrating Eq.(9)over spatial degrees of freedom.On the other hand,the effective Hamiltonian of the fine and hyperfine structures ofπ3He+is

where the corresponding fine- and hyperfine-structure coefficients areε1,ε2,ε3,andε4.The relevant reduced matrix elements involved in calculatingεiare

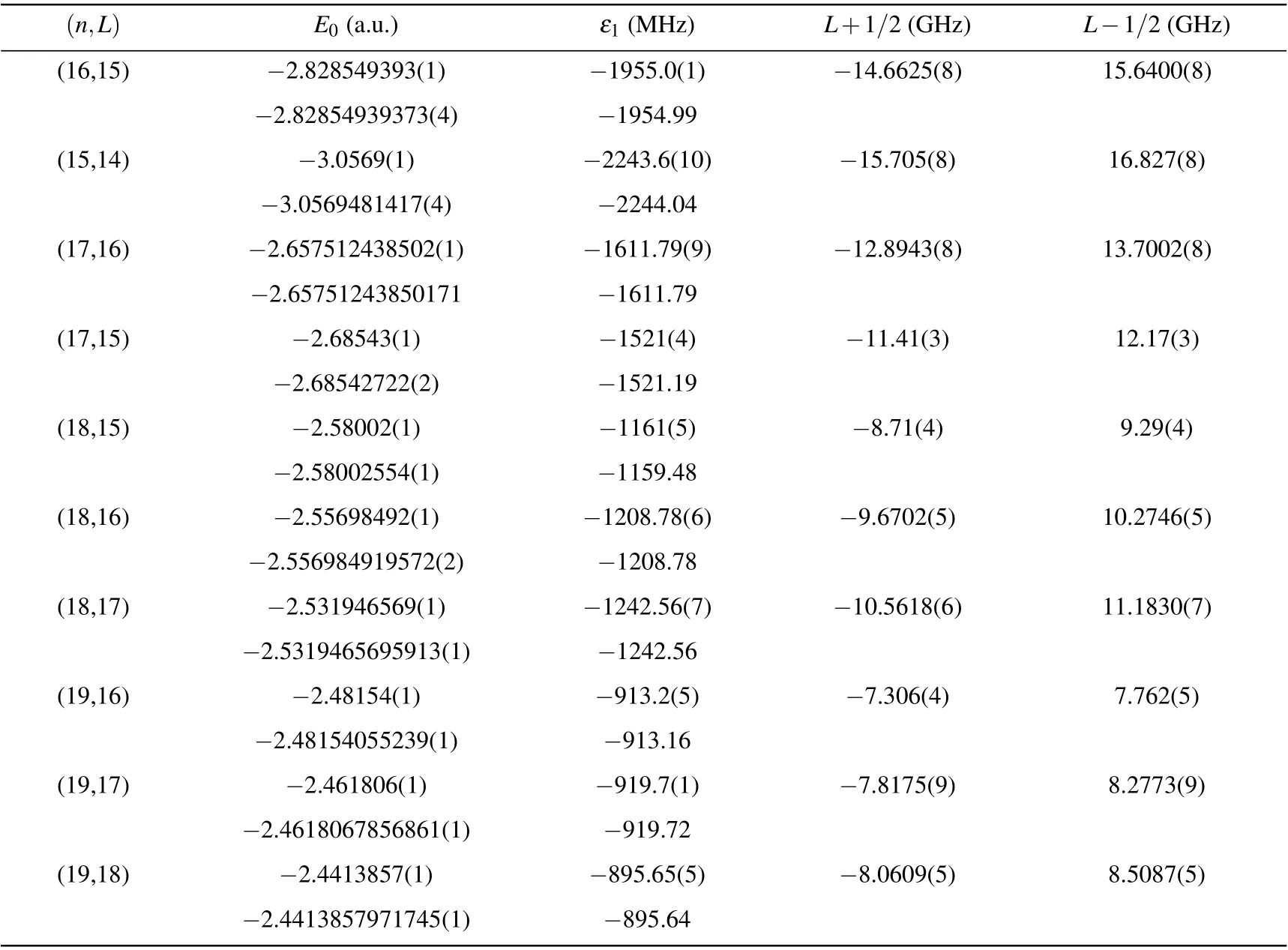
Table 4.Nonrelativistic energies E0, fine-structure coefficients ε1, and fine-structure state energies relative to E0, designated by the total angular momentum J=L±1/2,for the case of π4He+.The second entries are from Ref.[1]for comparison.

Table 5.Nonrelativistic energies E0 and fine and hyperfine-structure coefficients εi,i=1,2,3,4,for the case of π3He+.The second entries are from Ref.[1]for comparison.

Table 6.Hyperfine structure state energies(in units of GHz),relative to the nonrelativistic energies,for the case of π3He+,where the hyperfine states are designated by(J,F).

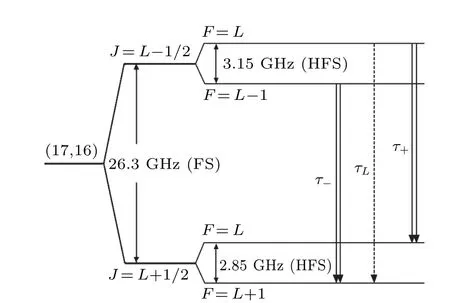
Fig.1.Schematic diagram of hyperfine sublevels of the(17,16)state of π3He+ atom.

Figure 1 shows three transitions within the(17,16)manifold ofπ3He+.Using the values listed in Table 6, one can obtain the theoretical values for the transition frequencies

The difference betweenτ+andτ-is nearly proportional to the helion magnetic moment[22]and has a value

It is noted that measurements of hyperfine structure in antiprotonic helium ˉp4He+have been performed by the ASACUSA group,[23,24]which agree with QED calculations[22]of ordermα6.Thus, our theoretical prediction in Eq.(14) forπ3He+may provide a reference for future experiments at PSI.However, in order to achieve improved theoretical results forτ+andτ-,a complete QED calculation of ordermα6is required to provide corrections to the coefficientsε1-ε4.

4.Summary

In conclusion, the wave functions along with the corresponding nonrelativistic energies were calculated variationally by using Hylleraas-type basis sets within the Feshbach closedchannel approximation.For long-lived states, energy eigenvalues were calculated to a precision of 10-10.But for shortlived states, the numerical uncertainties were quite large due to large widths.In this case, the CCR method can be used to improve the numerical accuracy.[25,26]The expectation values of the Breit operators were evaluated perturbatively.We presented the results of the fine and hyperfine structures for some experimentally relevant metastable states ofπ3,4He+within the framework of the Breit-Pauli Hamiltonian, at 10-4level of accuracy.In particular, the hyperfine-structure coefficients ofπ3He+were calculated for the first time.Our work will provide useful information for future precision measurements on pionic helium systems.

Acknowledgements

Project supported by the National Natural Science Foundation of China(Grant Nos.11974382 and 11474316).ZCY acknowledges the support from NSERC and SHARCnet of Canada.