Yang-He Chen(陳洋河), Bo Ji(季波), Nian-Qin Li(李念芹), Zhen Jiang(姜震), Wei Li(李維),Yu-Dong Li(李昱東), Liang-Sen Feng(馮梁森), Teng-Fei Wu(武騰飛), and Guang-Qiang He(何廣強),?

1SJTU Pinghu Institute of Intelligent Optoelectronics,Department of Electronic Engineering,Shanghai Jiao Tong University,Shanghai 200240,China

2State Key Laboratory of Advanced Optical Communication Systems and Networks,Department of Electronic Engineering,Shanghai Jiao Tong University,Shanghai 200240,China

3Science and Technology on Metrology and Calibration Laboratory,Changcheng Institute of Metrology&Measurement,Aviation Industry Corporation of China,Beijing 100095,China

Keywords: hyperentanglement,nonlinear photonic crystal,quasi-phase-matching

1.Introduction

Quantum entanglement is a fascinating and captivating phenomenon in quantum mechanics.It plays a crucial role in areas such as quantum computing,[1-3]quantum communication,[4-7]quantum cryptography,[8,9]quantum imaging,[10,11]and quantum precision measurement.[12]By harnessing quantum entanglement, we can achieve faster and more secure communication,[13,14]efficient computational methods,[15]and breakthroughs in encryption technology.[16]

Hyperentanglement is an intriguing extension of the phenomenon of quantum entanglement that pushes the boundaries of our understanding and exploration of the quantum world.Hyperentanglement refers to a quantum state with entanglement in multiple degrees of freedom,such as polarization,frequency,path,time,and orbital angular momentum.[17]This intricate entanglement creates a vast and intricate quantum state space, offering unprecedented opportunities for information processing and communication.[18]One of the most fascinating aspects of hyperentanglement is its potential for enhancing quantum communication protocols.By exploiting multiple degrees of freedom, hyperentanglement allows for more efficient transmission of information and increases resistance to noise.[19]Such advancements pave the way for significant applications in secure quantum key distribution,[20,21]quantum teleportation,[22]and quantum cryptography.[23,24]

The generation of hyperentangled photon pairs through the spontaneous parametric down-conversion(SPDC)process in nonlinear photonic crystals(NPC)[25-28]with second-order susceptibilityχ(2)is widely employed in research.Specifically,photonic crystals such as periodically poled lithium niobate (PPLN) and periodically poled potassium titanyl phosphate(PPKTP),designed using quasi-phase matching(QPM)technology, enable a range of optical parametric processes,possessing both high efficiency and flexibility.[29-31]This versatility facilitates advanced scientific investigations into novel quantum entanglement sources, contributing to cutting-edge research in the field.

The state of art technique for fabricating two-dimensional NPCs involves a combination of advanced lithography techniques, materials engineering, and nanofabrication methods.Electron beam(EB)lithography is a high-resolution patterning technique that uses a focused beam of electrons to selectively expose a material.[32]Without any static bias, Heet al.realized the fabrication of two-dimensional ferroelectric domainreversed structures in lithium niobate using EB lithography at room temperature.[33]In addition, ultrafast laser writing is also a promising fabrication technique for controlling precise two-dimensional NPC structures,and it can achieve threedimensional NPC fabrication with nanoscale resolution by either writing or erasing domain structures in the crystal.[34,35]Another commonly used technique in NPC fabrication is electrical poling,which involves applying a high voltage to a specific region of the crystal, resulting in the flipping of itsχ(2).In our work, considering that the two-dimensional NPC we designed only has a resolution at the micrometer scale,it can be easily achieved through electrical poling.

In this paper, we first introduce our compact pathfrequency hyperentanglement scheme and basic parameters of the designed nonlinear photonic crystal.Then we give the theoretical model of our hyperentangled source using quantum optics theory.Finally the joint-spectral amplitude (JSA) of the generated photon pair is calculated,with Schmidt decomposition on it, demonstrating a strong frequency correlation between the generated two photons.

2.Overall hyperentanglement scheme

We plan and design specific spontaneous parametric down-conversion processes to generate path-frequency hyperentangled photon pair.SPDC processes will take place when both energy conservation and momentum conservation are satisfied.We design a two-dimensional periodicalχ(2)nonlinear photonic crystal to compensate for the phase mismatch in the SPDC processes,i.e.,to satisfy quasi-phase-match conditions in the plane perpendicular to the pump beam.Our theoretical scheme is shown in Fig.1(a).A type-I (e→o+o)phase-matched 5%MgO-doped lithium niobate is selected as the material of our NPC and the temperature is set as room temperature(25?C).

Our scheme of path-frequency hyperentanglement totally includes 6 different paths and 2 different frequencies.As shown in Fig.1(b), each path is labeled by a unique angleθi(i= 1,2,3,4,5,6) on thexOyplane, and two generated frequenciesω1andω2satisfy the energy conservationωP=ω1+ω2.

Along thez-axis,the momentum is fully conserved which means a perfect phase match

where the subscriptzrefers to thezcomponent and?is the angle between the signal (or idler) photon’s momentum andz-axis.The angle?can be deduced after the frequencies of pump,signal,and idler are chosen.

However,because of the difference between the frequencies of signal and idler photons,momentum mismatch appears in thexOyplane as follows:

In our scheme,we set the wavelength of the pump beam asλP=775 nm (in vacuum, same below), and chooseλS=1530 nm,λI= 1570.5 nm, which belong to the communication band.Then we can calculatef1=c/λI=190.9 THz andf2=c/λS= 195.9 THz.The corresponding refractive indices of pump light, signal light, and idler light arenP=2.1707,nS=2.2095, andnI=2.2082, respectively.According to Eqs.(1) and (2), we can obtain?= 0.186 rad and?k=0.0443μm-1.

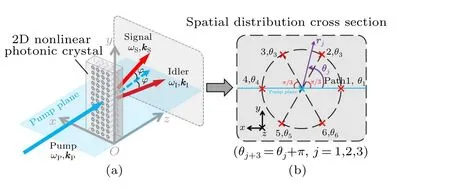
Fig.1.(a) Our scheme of path-frequency hyperentanglement using a designed two-dimensional NPC.The second order susceptibility χ(2) of NPC is periodically modified in the xOy plane in order to compensate the momentum mismatch perpendicular to the pump beam.Perfect phase match is achieved along the z axis.(b)Spatial distribution cross section.

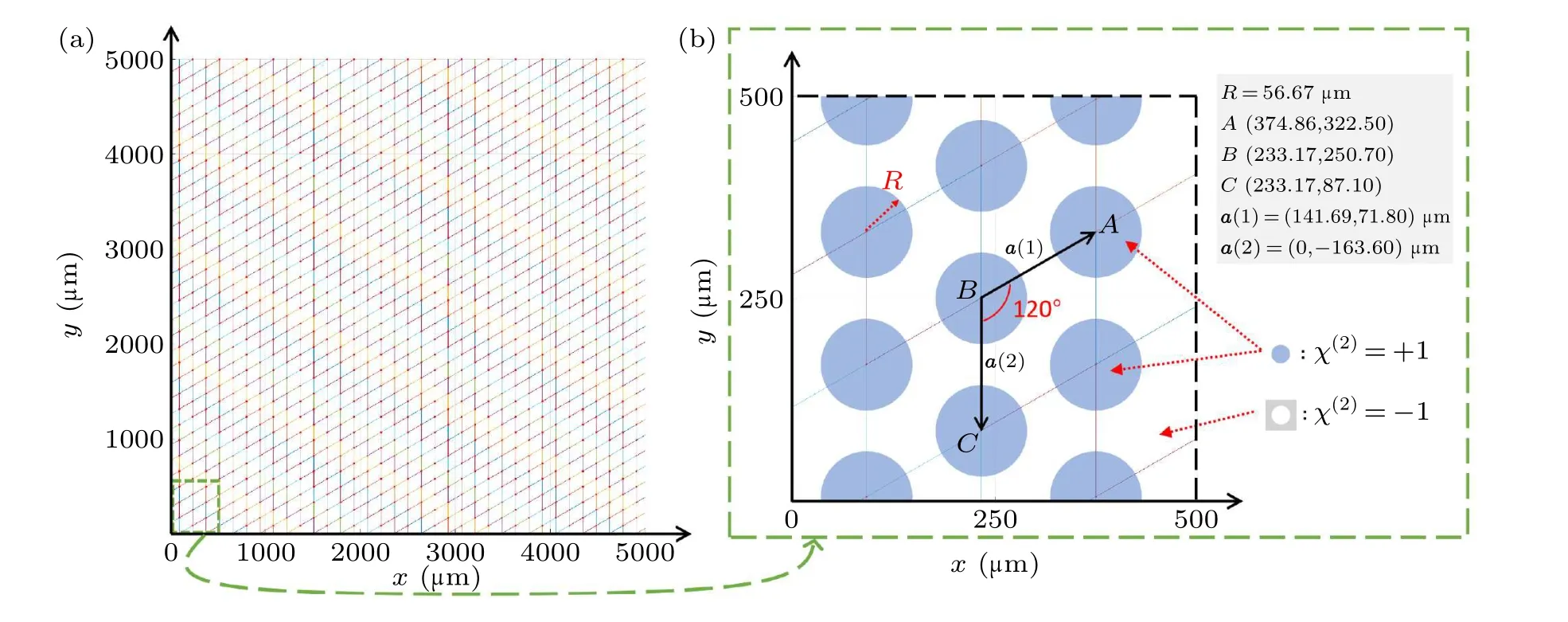
Fig.2.(a)Lattice structure of the χ(2) susceptibility design example of our NPC(i.e.,u(r)).(b)Convolution of lattice and circular motif(i.e.,u(r)?s(r)),indicating the distribution of χ(2) in the xOy plane with accurate structure parameters.

The momentum mismatches of the six SPDC processes have the same numerical value and each possesses a unique direction.That is,the momentum mismatch vectors are evenly distributed on one circumference

whereθis the directed angles between the projection of the signal’s(or idler’s)momentum on thexOyplane and the positive direction of thex-axis,and the subscriptirefers to theith angle of the corresponding SPDC process.

The momentum mismatches can be perfectly compensated through the periodic poling method.[36,37]By periodically modifying the susceptibility of NPC in real space,we can obtain six peak values in its Fourier space (reciprocal space)to perform QPM.The designed distribution of NPC’sχ(2)is shown in Fig.2.

The second order susceptibilityχ(2)of our NPC can be mathematically expressed asg(r)=a(r)×(u(r)?s(r)),wherea(r)denotes the area of the NPC,u(r)is a sum of delta functions referring to the lattice structure of NPC,ands(r)is the motif function.

Circular motif with a radius of 56.67μm-1is selected.In the motifχ(2)=+1, whileχ(2)=-1 in the rest area of the NPC.We fix the relative radius of motifR/a=0.2.

We then further check our design by viewing the NPC in the Fourier domain,as shown in Fig.3.The six arrows indicate the six mismatch vectors of six SPDC processes.We conclude that the QPM conditions are satisfied using the design.

Using the design example above,we are going to make a brief discussion on the relationship between the direction and frequency of the generated photons.We first fix the azimuth angle of the emitted signal(idler)photons:θS=0,θI=π,and use the QPM conditions to calculate the relationship between?m(m=S,I)and signal photon’s wavelength.The results are shown in Fig.4.

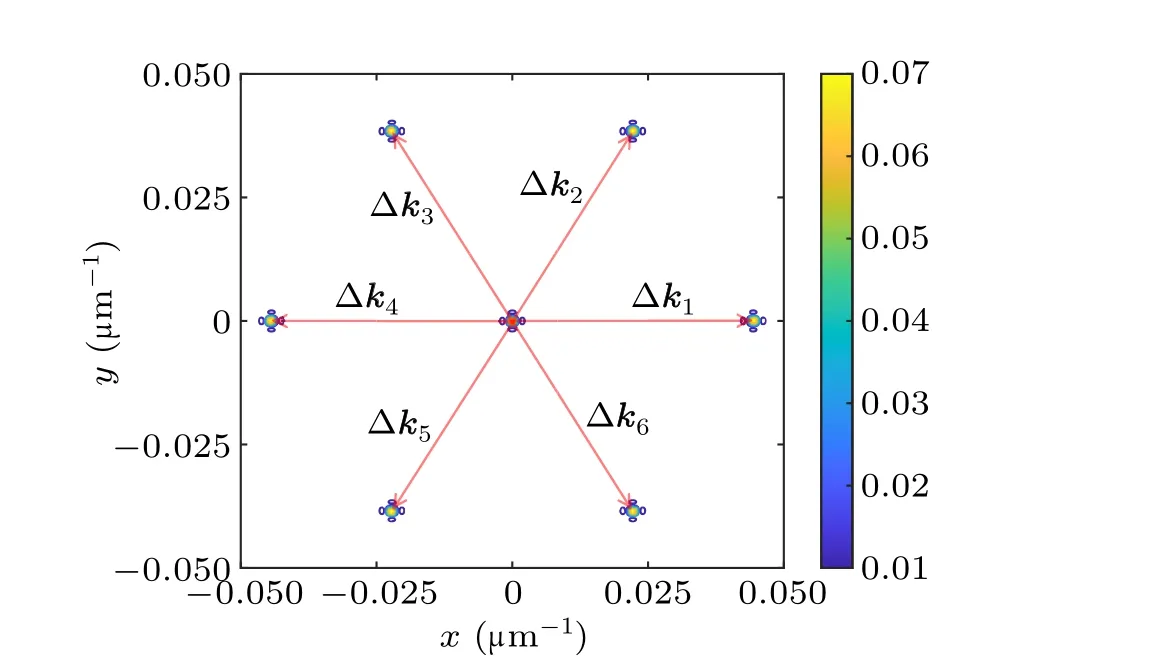
Fig.3.The χ(2) susceptibility distribution of designed NPC in Fourier space.The six peaks correspond to six momentum mismatches of expected SPDC processes, which means the QPM conditions are satisfied through the designed NPC.

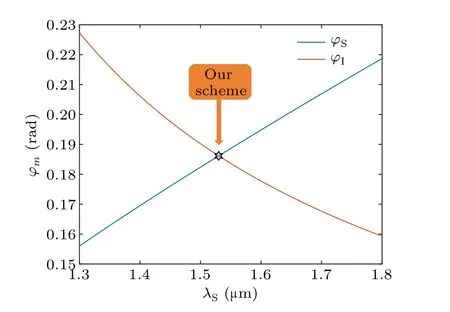
Fig.4.Relationship between ?m (m=S,I) and signal photon’s wavelength. ?m (m=S,I) refers to the angle between the pump beam and signal(idler).In our scheme,?S=?I ensures the symmetry of signal and idler.

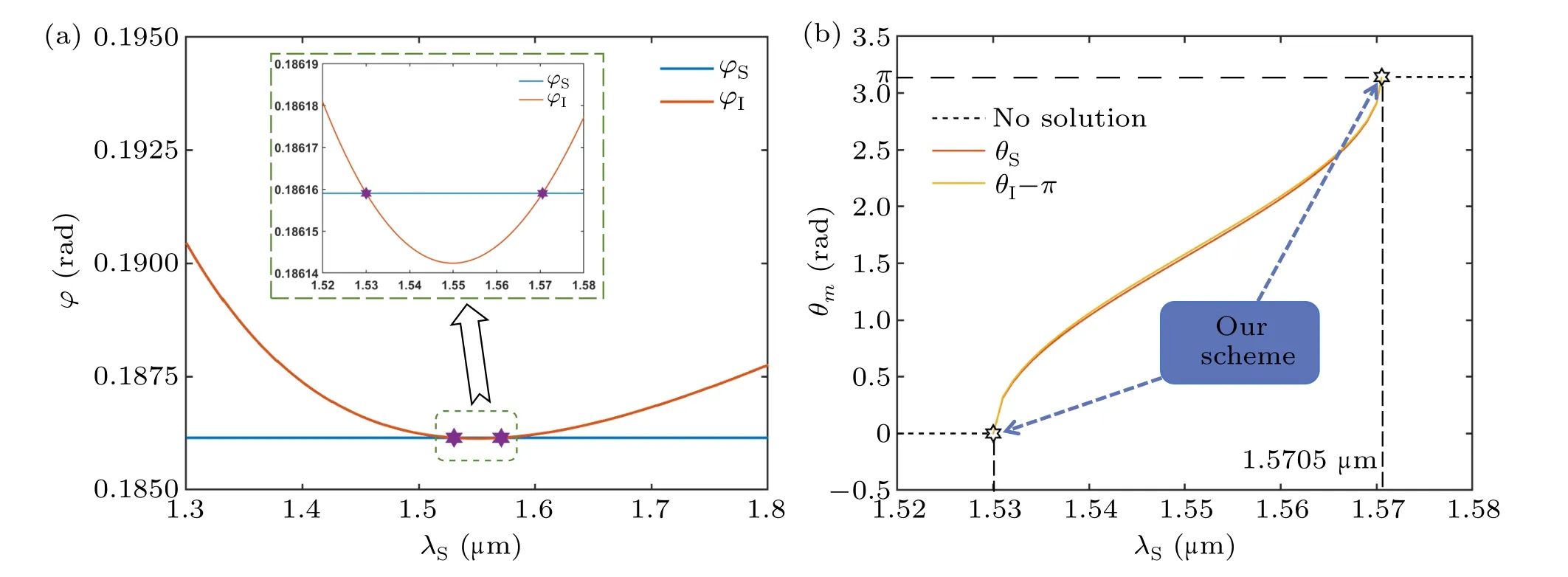
Fig.5.(a) The angle between pump beam and idler (?I) varies with the signal’s wavelength (λS) when ?S is fixed, where the perfect phase matching condition is always maintained.The intersection of two curves corresponds to our scheme.Due to the symmetry of f1 and f2 with respect to fP/2, there are two intersections in the graph.(b) The azimuth angles of generated photons (θm, m=S,I) vary with the signal’s wavelength(λS)when ? is fixed.Two curves are approximately coincident because the signal and idler’s wave vectors are much larger than the momentum mismatch compensated by the designed NPC.Both ends of the curve correspond to two of the six expected SPDC processes in our scheme.

Then we fix the angle?S=0.186 rad to analyze the relationship between other direction angles and signal photon’s wavelength.The other three angles are obtained using the three-dimensional vector equation of phase match.The results are shown in Fig.5.

The analysis above indicates the path-frequency relationship along two orthogonal directions.In fact,our scheme has good scalability and can be easily extended to the case of signal light and idler light at different frequencies,while the calculation and design processes are similar.The angle?and value of mismatch vector ?kwill be different.Therefore, it is necessary to change the poling period of nonlinear photonic crystals.At this point, the NPC’s lattice structureu(r)needs to be correspondingly reduced or amplified.If we want to expand the number of paths to more than six,we need to utilize quasi-periodic poling nonlinear photonic crystals to compensate for more wave vector mismatches and meet more quasiphase-matching conditions.However, at this point, due to its Fourier transform domain having smaller peaks at the corresponding mismatch than in the case of periodic poling, and having peaks at other mismatches, the conversion efficiency will decrease.

3.Theoretical model

We will derive the theoretical expression of the generated path-frequency hyperentangled biphoton state.In the interaction picture, the evolution of the quantum state with time satisfies the following equation:[38]is JSA for the process where the signal photon propagates along pathθ1and the idler photon propagates along pathθ1+π,|S,θ1,ωS〉= ?a?S,kS,θ1|0〉S,and|I,θ1+π,ωI〉= ?a?I,kI,θ1+π|0〉I.The phase mismatch on thexOyplane for this process is denoted as ?k⊥1.A2(ωS,ωI),...,A6(ωS,ωI) can be obtained similarly.

The photon flux can be estimated by[39-41]

Equation(13)is the final expression of our path-frequency hyperentangled biphoton state.

4.Frequency correlations of two-photon pairs

We theoretically calculate the JSA of the generated photon pair,as shown in Fig.6.Specifically,we set the full width at half maxima (FWHM) of the input continuous pump light to 0.1 nm.The frequency center of the simulated JSA isfP/2,the bandwidth is 8 THz, and the momentum mismatch ?kis fixed at 0.0443μm-1.We should note that the FWHM of the pump light needs to be narrow enough to ensure high degree of entanglement.In practice, the lattice structure parameters of nonlinear photonic crystals require very precise fabrication,as it directly affects ?kthat the crystal can provide, thereby affecting the conversion efficiency of nonlinear processes.

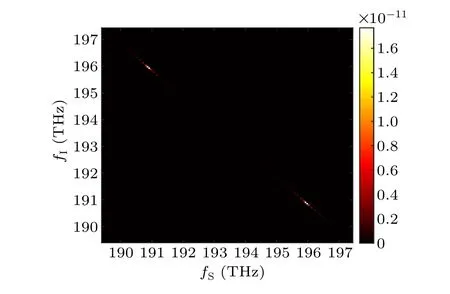
Fig.6.JSA(A(ωS,ωI))of the generated hyperentangled photon pair.

To investigate frequency entanglement property, we can perform Schmidt decomposition onA(ωS,ωI), that is,[42]

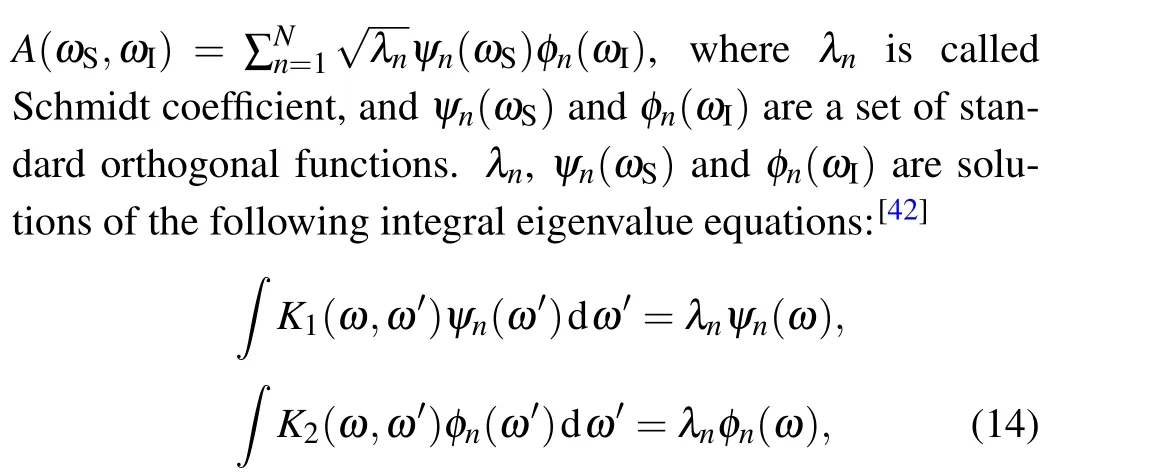
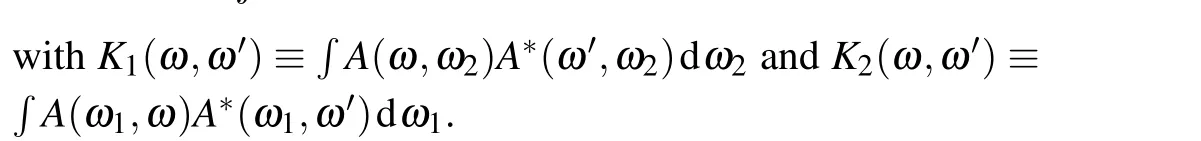
The first 12 Schmidt coefficients, arranged from largest to smallest, are shown in Fig.7(a).Note that the latter coefficients are close to 0 and their contributions to the degree of entanglement are negligible.BecauseA(ωS,ωI)is symmetric with respect tofP/2, Schmidt coefficients always appear in pairs,that is,λ2k=λ2k+1(k ∈Z).Based on the eigenvalueλnobtained from the Schmidt decomposition, we can calculate the entropySof entanglement and effective Schmidt rankKto characterize the degree of frequency entanglement,which are defined as

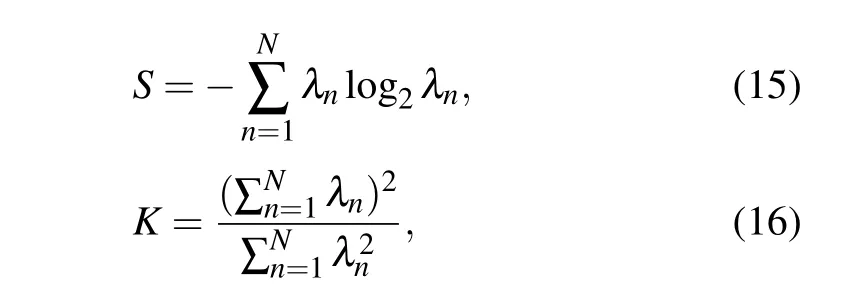
respectively.S>0 andK>1 both indicate the presence of entanglement,and the larger value indicates the higher degree of entanglement.The JSA is first normalized and then solved to obtain the Schmidt coefficients in the Schmidt decomposition.The calculated effective Schmidt rankK=6.4675>1,andSfinally converges to 3.2789, demonstrating strong frequency correlation between the generated two photons around two discrete frequenciesf1andf2.Figure 7(b)shows the first 30 iterations ofS.

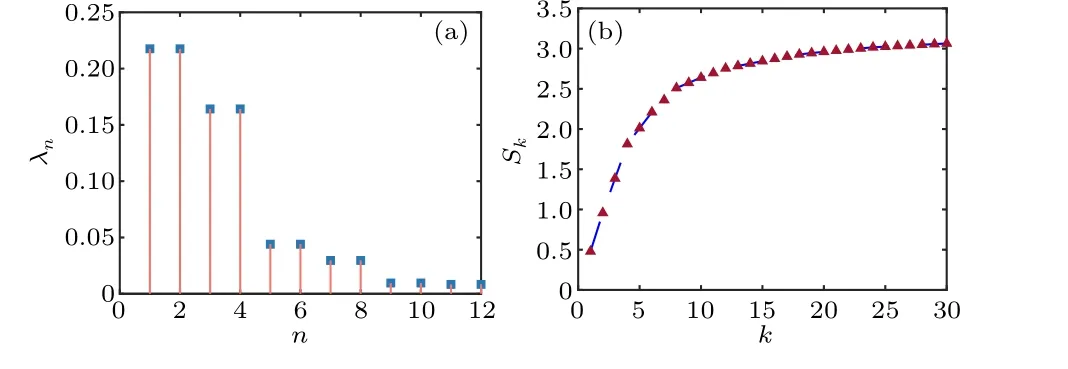
Fig.7.(a) The maximum 12 Schmidt coefficients.Schmidt coefficients appear in pairs because of the symmetry with respect to fP/2 of A(ωS,ωI).(b)The first 30 iterations of entropy S of entanglement.

The first eight basis functions in the Schmidt decomposition are shown in Fig.8,from which we can see the orthogonality of each basis function.Because of the symmetry with respect tofP/2 ofA(ωS,ωI),ψnandφnare divided into two groups,distributed aroundf1andf2,respectively.It is worth mentioning thatψnandφnhave the same shape due to type-I quasi-phase-matching conditions, which means that both signal and idler photons have the same ordinary field mode.

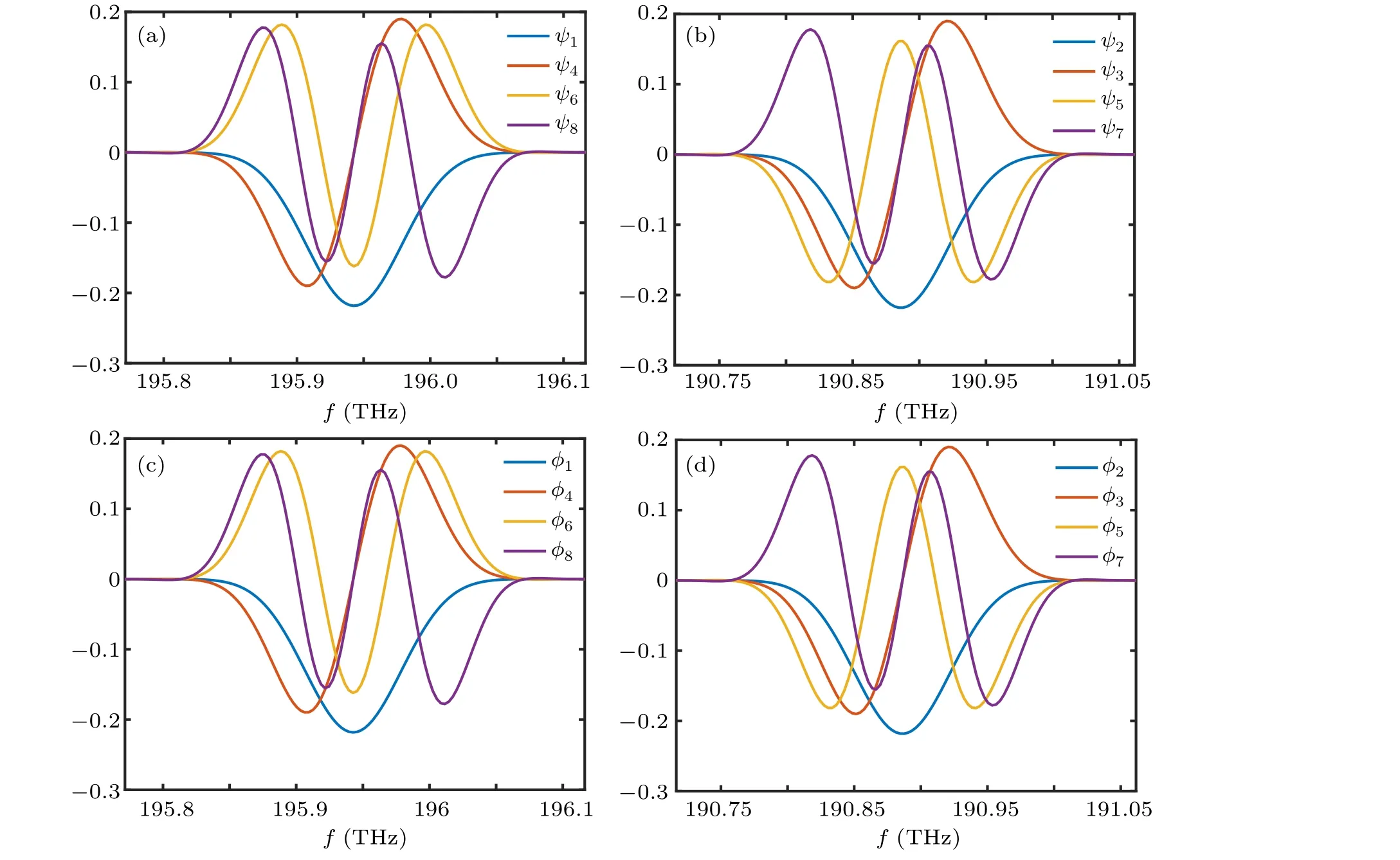
Fig.8.The first eight basis functions(a)and(b)ψn and(c)and(d)φn.

5.Conclusion

We propose a compact path-frequency hyperentangled quantum light source based on type-I quasi-phase-matched NPC.A two-dimensional periodicalχ(2)NPC is designed to realize quasi-phase-matching in the plane perpendicular to the incident pump beam, including six different paths and two different frequencies.We derive the theoretical expression for the generated two-photon state in detail and estimate the photon flux of our source, which can reach 2.068×105pairs·s-1·mm-2.JSA has been calculated and the resulting entropySof entanglement and effective Schmidt rankKare 3.2789 and 6.4675, respectively, indicating strong frequency correlation between the generated two photons.As NPC manufacturing technology continues to advance,the possibilities for our two-dimensional NPC scheme are expanding into three dimensions.[34]This advancement opens up promising avenues for future applications in quantum holography,quantum information processing, and long-distance quantum communication.

Acknowledgments

Project supported by the Key-Area Research and Development Program of Guangdong Province of China (Grant No.2018B030325002), the National Natural Science Foundation of China (Grant No.62075129), the Open Project Program of SJTU-Pinghu Institute of Intelligent Optoelectronics (Grant No.2022SPIOE204), the Science and Technology on Metrology and Calibration Laboratory (Grant No.JLJK2022001B002),and the Sichuan Provincial Key Laboratory of Microwave Photonics(Grant No.2023-04).