Xin Liu(劉欣), Meng-Yu Tian(田夢(mèng)雨), Xiao-Ning Cui(崔曉寧), and Xin-He Zhang(張馨鶴)

1School of Physics and Technology,University of Jinan,Jinan 250022,China

2Marketing Service Center(Center of Metrology),State Grid ShanDong Electric Power Company,Jinan 250001,China

Keywords: photon blockade,single photon source,quantum interference

1.Introduction

Single photon is an important resource in secure quantum key distribution,[1]quantum network,[2]and quantum computation.[3]In decades, great efforts have been devoted to generation of single photons, including parametric driven nonlinear media[4–6]and manipulation of single trapped quantum emitter.[7–9]Among these methods,single photon source based on photon blockade (PB) is an promising approach, which get great advantage both in theories and experiments.[10–21]Proposes in circuit-QED systems,[22]Kerr-type nonlinear cavities,[23]and optomechanical systems[24]have been developed and experimentally demonstrated.[25–27]A PB based single photon source is usually divided into three types: conventional photon blockade (CPB), which emerges due to the nonlinearity of the system eigenvalues,[13]unconventional photon blockade(UPB),which occurs due to destructive interferences between different transition pathways,[28]and photon blockade induced by truncation of Hilbert space, as observed in quantum linear scissors.[29]UPB was found first by Liew and Savona,[30,31]and has been studied in a optical cavity with a quantum dot,[32,33]weakly nonlinear photonicmolecules,[34]coupled optomechanical systems,[35]coupled cavities with second-order nonlinearity,[36]coupled cavities with thirdorder nonlinearity,[37]spinning anharmonic resonator.[38]Recently,UPB in two-photon transition processes have triggered much attention,[39–42]and other multi-photon processes have been discovered in these processes.[43]In this work,we study a system of two-photon Jaynes–Cummings model with twofrequency cavity drivings and atom driving.It is found that by setting the driving strengths properly, the photons in the cavity mode exhibit antibunching property.The zero-delay second-order correlation function isg(2)(0)≈0.05, which is lower than that in Ref.[42].Analytical and numerical results reveal that antibunching phenomena are due to interference between different transition pathways.Smooth variations ofg(2)(0)with variations of driving strengths manifest that these UPB phenomena are robust with small fluctuations of driving strengths.

The rest of the paper is organized as follows.In Section 2,we introduce the setup and Hamiltonian of the system.In Section 3, we analytically calculate the expression of the zerodelay second-order correlation function and obtain an optimal condition for the photon blockade.Numerical simulation and discussion of experimental feasibility are present in Section 4 with a brief conclusion in Section 5.

2.Setup and model

We consider a setup composed of a cavity coupled to a two-level atom via a two-photon interaction, with the cavity driven by laser of frequencyωrand laser of frequency 2ωrand the atom driven by laser of frequencyωqas illustrated in Fig.1(a).The system Hamiltonian reads(hereafter ˉh=1)

wherea?andadenote the creation and annihilation operators of the cavity mode of frequencyωr;σ+andσ-denote the rasing and lowering operators of the two-level atom with an energy separation ofωqbetween the excited state|e〉and the ground state|g〉.The third term represents the two-photon interaction between the cavity mode and the atom with interaction strengthg.The cavity is driven by a laser of frequencyωrwith strengthE/2 and a laser of frequency 2ωrwith strengthF/2 and phase differenceθcompared to the first laser,which can be implemented by a second-order nonlinearity process.[42]The atom is driven by another laser of frequencyωqwith strength?/2 and phase difference?compared to the first laser.We choose the frequencies of the cavity and the atom in a two-photon resonant case, i.e.,ωq=2ωr.Thus,the Hamiltonian in the interaction picture reads

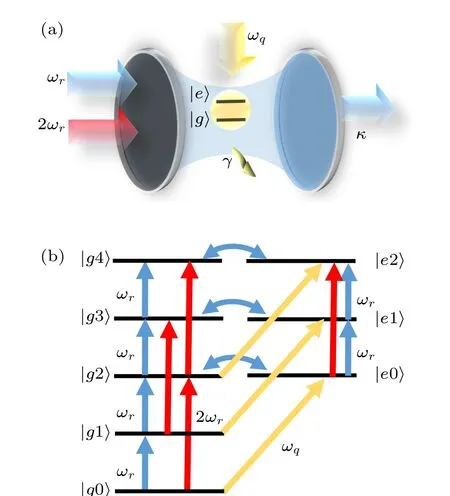
Fig.1.(a)Schematic of the setup considered,which consists of a cavity coupled to a two-level atom via a two-photon interaction, with the cavity driven by laser of frequency ωr and laser of frequency 2ωr and the atom driven by laser of frequency ωq.The cavity decays with rate κ and the atom decays with rate γ.(b) Eight lowest bare-state energy levels of the system and their transition pathways.

We consider the weak driving and bad cavity case, i.e.,κ ?F,E,?,g.In this situation the higher states are rarely populated, so we can only consider the lowest energy levels.In Fig.1(b),eight lowest bare-state energy levels of the system and their transition pathways are depicted.When the transition pathways|g0〉→|g1〉→|g2〉,|g0〉→|g2〉, and|g0〉→|e0〉→|g2〉 destructively interfere, the two-photon state|g2〉cannot be occupied and the unconventional photon blockade occurs.To evaluate the strength of the unconventional photon blockade and the purity of single photons, the zero-delay second-order correlation functiong(2)(0)=〈a?a?aa〉/〈a?a〉2in steady state is usually used.Wheng(2)(0)?1,the photons are antibunching and a single-photon source is realized.

3.Analytical expression of zero-delay secondorder correlation function

To obtain an analytical expression of the zero-delay second-order correlation function, we introduce the non-Hermite Hamiltonian

Under the weak driving condition, the probability amplitudes scale asC1(t)?{C2(t),C4(t)} ?{C3(t),C6(t)} ?C5(t),C8(t)?C7(t).The equations of motion forCi(t) can be approximately solved by a perturbation method, i.e., discard the higher-order terms in the equations of motion for the lower-order variables.By assumingC1(t)=1,the steady-state solutions of the probability amplitudes can be obtained by setting?Ci(t)/?t=0 as

A case corresponding to a perfect photon blockade isC3=0,which means that there is no two-photon probability in the cavity mode.A further suppression of the multi-photon excitation could be realized by minimizing the probability amplitudeC5of state|g3〉.Unfortunately, the probability amplitudesC3andC5cannot be zero simultaneously due to the same component 2ig?ei?-Fγeiθ.To reduceC7andC8under the conditionC3=0, the two parts arising from the high frequency driving of cavity mode and driving of atom should have opposite symbols.Without loss of generality,we chooseθ=π/2,?=0, thus an optimal parameter condition can be obtained as

4.Simulation and discussion

To verify our analytical results, we perform numerical simulation base on a master equation method.Assuming that the cavity and the atom are connected with two individual vacuum baths, the system evolution is governed by the master equation

whereκ(γ) is the decay rate of the cavity (atom).By solving Eq.(25) numerically, a steady state density matrixρssis obtained and the zero-delay second-order correlation function is calculated asg(2)(0)=Tr[a?a?aaρss]/(Tr[a?aρss])2.In the same way,we can calculate occupied probability of each state as|Ci|2= Tr[|j〉〈j|ρss] for|j〉 representing|g0〉,|g1〉,|g2〉,|e0〉,|g3〉,|e2〉,|g4〉 or|e2〉.The average photon number of the cavity mode can also be calculated asn=Tr[a?aρss].

In our simulation,we truncated the photon number states space up to five photons under the weak driving assumption and the parameters are chosen to beωq=2ωr=8×2πGHz,g=0.01ωr,F=0.36g,?=10g,θ=π/2,?=0,κ=γ=100g,Evaries between 0 and 20g.In Fig.2(a), we plot the occupied probabilities of the lowest eight states as functions of the driving strengthE.It is verified that the probability amplitudes obeyC1≈1 andC1?{C2,C4} ?{C3,C6} ?{C5,C8} ?C7.The occupied probabilities|C2|2,|C6|2increase with the increase of driving strengthE.|C4|2depends on the driving strength?and the atom decay rateγ.|C5|2cannot be suppressed under the conditionC3=0.|C7|2and|C8|2are partly suppressed as shown in the figure by small dips of the lines.In Fig.2(b),we plot the correlation functiong(2)(0)and the average photon number〈a?a〉 of the cavity mode as functions of the driving strengthE.The red dotted line isg(2)(0) with cavity mode driven by lasers of two frequencies and without atom driving.The dot-dashed line isg(2)(0)with atom driving and low frequency cavity driving.The solid line isg(2)(0)with three drivings.It can be found that three transition pathways have effect on suppressing higher excitations.There is a dip ofg(2)(0)≈0.05 at a value ofEdetermined by Eq.(24).The dip ofg(2)(0)is at the same value ofEwith the dip of occupied probability|C3|2,which indicates that the optimal photon blockade occurs due to the quantum interference of different transition pathways.The inset in Fig.2(b) describes the increase of the average photon number〈a?a〉with the increase of the driving strengthEas a natural result.

To verify the optimal condition for the photon blockade,i.e., Eq.(24) and photon blockade robustness with parameter fluctuations,we plot theg(2)(0)as functions ofE,F,and?in Fig.3.The black dashed lines indicate the optimal condition of the photon blockade determined by Eq.(24).In Figs.3(a)–3(c), the lines of optimal condition match well with the numerical results obtained by the master equation in most of the region.The higherg(2)(0) in some regions with very small driving strengths are due to the constant strength of the third driving,which induces a bunching effect of the photons in the cavity mode.The simulations indicate that the photon blockade in our system is robust with small parameter fluctuations.

Our proposal can be implemented in a superconducting quantum circuit, which can realize a coupling strengthg=0.01ωr=40×2πMHz.[40]The frequency of a transmissionline resonator can vary between 1×2πGHz to 10×2πGHz.[44]The superconducting qubit acting as a twolevel atom can be addressed and driven individually by microwave.A large decay rate of the cavity mode can be realized by designing of coupling inductance,[45]and a Hanbury–Brown–Twiss test of the quantum correlation of emitted photons can be realized by measuring the moments of the two quadratures.[46]Our scheme can also be implemented by a Fabry–P′erot cavity as described in Ref.[47].

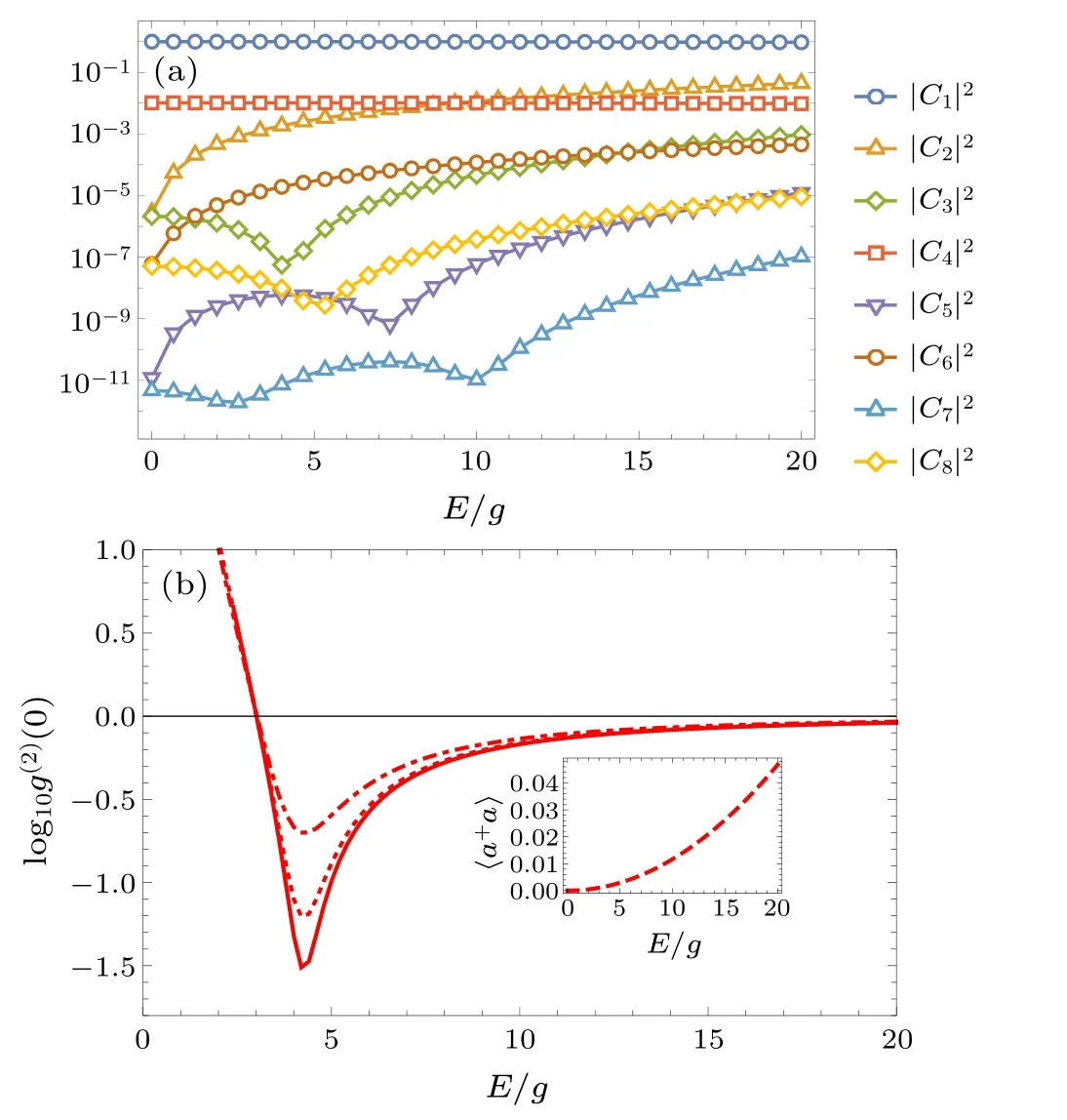
Fig.2.(a) The occupied probabilities of states |Ci|2 versus the driving strength E.(b) The zero-decay second-order correlation function g(2)(0)versus the driving strength E.The dotted line is g(2)(0)without atom driving,the dot-dashed line is g(2)(0)without high frequency cavity driving and the solid line is g(2)(0)with two-frequency cavity drivings and atom driving.The inset is the average photon number 〈a?a〉 versus the driving strength E.The parameters are ωq =2ωr =8×2π GHz, g=0.01ωr, F =0.36g,? =10g,θ =π/2,? =0,and κ =γ =100g.

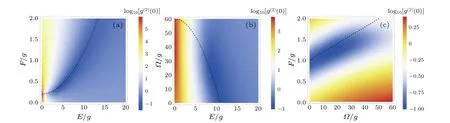
Fig.3.(a)The g(2)(0)versus the driving strength F and E.The other parameters are ωq=2ωr=8×2π GHz,g=0.01ωr,? =10g,θ =π/2, ? =0, and κ =γ =100g.(b) The g(2)(0) versus the driving strength ? and E.The other parameters are ωq =2ωr =8×2π GHz, g=0.01ωr, F =1.2g, θ =π/2, ? =0, and κ =γ =100g.(c)The g(2)(0)versus the driving strength F and ?.The other parameters are ωq=2ωr=8×2π GHz,g=0.01ωr,E=10g,θ =π/2,?=0,and κ=γ=100g.The black lines indicate the optimal condition determined by Eq.(24).

5.Conclusion

In summary, we have studied a system consisting of an atom coupled to a cavity with two-photon interaction.By choosing proper strength of atom driving and strengths of twofrequency cavity drivings, a prominent photon blockade can be obtained.We have analytically calculated the optimal condition for the photon blockade and found that three transition pathways can further reduce the zero-delay second-order correlation function compared with the cases of two transition pathways.Analytical results match well with the numerical results obtained by the master equation.The numerical results also reveal that the photon blockade in this system is robust against small fluctuations of parameters.The system can act as a single photon source.

Acknowledgment

Project supported by the National Natural Science Foundation of China(Grant No.61601196).