非齊型齊次Morrey-Herz空間中某些次線性算子和交換子的有界性

武江龍

(牡丹江師范學院數(shù)學系,黑龍江牡丹江 157012)

非齊型齊次Morrey-Herz空間中某些次線性算子和交換子的有界性

武江龍

(牡丹江師范學院數(shù)學系,黑龍江牡丹江 157012)

在非齊型齊次Morrey-Herz空間(μ)中建立了某些次線性算子的有界性,同時利用Calder′on-Zygmund算子的L2(μ)有界性,在(μ)上證明了由Calder′on-Zygmund算子和RBMO(μ)函數(shù)生成的交換子的有界性.

交換子;齊次Morrey-Herz空間;非二倍測度;RBMO(μ);次線性算子

1 引言

在經典調和分析中,一個關鍵的假設是測度滿足二倍條件.我們稱測度μ滿足二倍條件,是指如果存在常數(shù)C,使得對x∈suppμ,r＞0,有μ(B(x,2r))≤Cμ(B(x,r)),其中B(x,r)={y∈Rd:|y?x|＜r}.然而,最近幾年的研究表明,定義在歐氏空間Rd上的非負Radon測度μ不滿足二倍條件時,許多經典的結果仍然成立[15].對μ僅有的假設條件是增長性條件,即存在常數(shù)C0＞0,使得對任意的x∈Rd,r＞0,有

其中n為固定的數(shù)且0＜n≤d.如果歐氏空間Rd上賦予的Radon測度僅滿足增長性條件(1),則稱它為非齊型空間.眾所周知,二倍條件在齊型空間的分析中起著關鍵作用,這表明齊型空間上調和分析理論和非二倍測度下的結果是截然不同的[14].

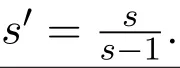
2 次線性算子在非齊型齊次Morrey-Herz空間中的有界性

在敘述主要結果之前,首先回顧一些基本概念.

對于k∈Z,令Bk={x∈Rd:|x|≤2k},Ak=BkBk?1和χk=χAk,其中χAk表示集合Ak的特征函數(shù).

其中Q?Rd為各邊平行于坐標軸的閉方體,l(Q)表示其邊長.文[11]證明了極大函數(shù)M在Lq(μ)(1＜q＜∞)中有界.并且容易驗證M滿足定理2.1中的尺寸條件(i)和(ii).從而有

推論2.2設α,λ,p和q如定理2.1中所述,則由(4)式定義的極大函數(shù)M在中有界.

注當λ=0時,上面的結果和文[8]中得到的結果是一致的.

3 交換子在非齊型齊次Morrey-Herz空間中的有界性

本節(jié)主要討論Calder′on-Zygmund算子和RBMO(μ)函數(shù)生成的交換子在齊次Morrey-Herz空間中的有界性.

對于給定的常數(shù)γ＞1,β＞γn及βd=2inf β,稱某個方體Q?Rd是一個(γ,β)倍方體是指Q滿足μ(γQ)≤βμ(Q),其中γQ表示與Q同心,邊長為γl(Q)的方體.對于Rd中給定的兩個方體Q1?Q2,定義

從而由引理3.1得

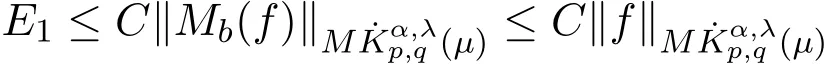
對E3,注意到,當x∈Ak,j≥k+2以及y∈Aj時,有|x?y|～|y|,因此,對j≥k+2,運用RBMO(μ)函數(shù)的性質,H¨older不等式,K?Qk,?Qj≤C(j?k?1),(a),增長性條件(1)及文[4]中的推論3.5,有

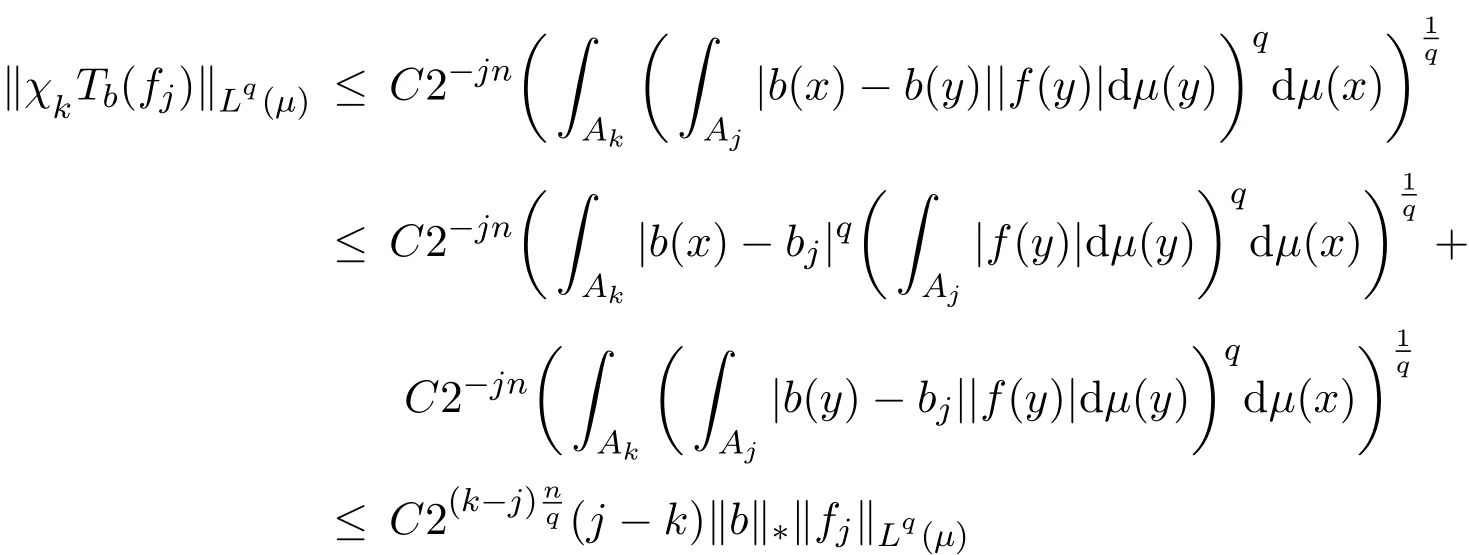
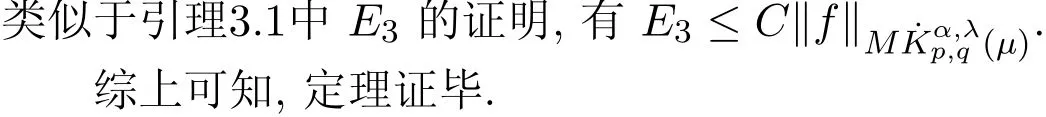
注當λ=0時,上面的結果和文[8]中得到的結果是一致的.

[1]Orobitg J,P′erez C.Apweights for non doubling measures in Rnand applications[J].Trans.Amer.Math. Soc.,2002,354:2013-2033.

[2]Hu Guoen,Meng Yan,Yang Dachun.New atomic characterization of H1space with non-doubling measures and its applications[J].Math.Proc.Cambridge Philos.Soc.,2005,138(1):151-171.

[3]Hu Guoen,Meng Yan,Yang Dachun.Multilinear commutators of singular integrals with non doubling measures[J].Integral Equations Operator Theory,2005,51(2):235-255.

[4]Tolsa X.BMO,H1and Calder′on-Zygmund operators for non doubling measures[J].Math.Ann.,2001, 319:89-149.

[5]Tolsa X.Littlewood-Paley theory and the T(1)theorem with non-doubling measures[J].Adv.Math.,2001, 164:57-116.

[6]Li Xinwei,Yang Dachun.Boundedness of some subinear operators on Herz spaces[J].Illinois J.of Math., 1996,40:485-501.

[7]Lu Shanzhen,Yang Dachun.The continucity of commutators on Herz-type spaces[J].Michigan Math.J., 1997,44:255-281.

[8]郭燕,孟巖.某些次線性算子和交換子在非齊型空間上的Herz空間中的有界性[J].北京師范大學學報:自然科學版,2004,40(6):725-731.

[9]趙向青,高文華.線性算子在Herz-Morrey空間上的有界性[J].高校應用數(shù)學學報:A輯,2005,20(1):55-62.

[10]孟巖.非倍測度空間上極大交換子有界性的新證明[J].北京師范大學學報:自然科學版,2004,40(3):309-314.

[11]Garc′?a-Cuerva J,Martell J M.Two-weight norm inequalities for maximal operators and fractionals on non-homogeneous spaces[J].Indiana Univ.Math.J.,2001,50:1241-1280.

Boundedness of some sublinear operators and commutators on homogeneous Morrey-Herz spaces with non doubling measures

WU Jiang-long
(Department of Mathematics,Mudanjiang Normal College,Mudanjiang157012,China)

The boundedness of some sublinear operators is established on homogeneous Morrey-Herz spaces with non-doubling measures.At the same time,this paper using the L2(μ)boundedness of Calder′on-Zygmund operators to prove the boundedness of commutators generated by Calder′on-Zygmund operators with RBMO(μ) functions on

commutator,homogeneous Morrey-Herz space,non-doubling measure,RBMO(μ),sublinear operator

O174

A

1008-5513(2009)03-0586-09

2007-06-21.

牡丹江師范學院科研項目(KZ2008001).

武江龍(1980-),碩士,研究方向：調和分析.

2000MSC:42B25