賦廣義Orlicz范數(shù)的Orlicz空間中kx的兩個特征

許 晶,崔云安,莊彩彩

(1.通化師范學(xué)院 數(shù)學(xué)系,吉林 通化 134002;2.哈爾濱理工大學(xué) 應(yīng)用科學(xué)學(xué)院,黑龍江 哈爾濱 150080)

1 引 言

2 定義及符號

稱N-函數(shù)M(u)滿足△2條件,如果存在常數(shù)K≥2和u0≥0滿足M(2u)≤KM(u)(u≥u0).我們總用M(u)∈△2表示M(u)滿足△2條件;用M(u)∈▽2表示它的余函數(shù)N(v)∈△2.

3 主要結(jié)果及證明

定理1 inf{kx∶‖x‖M,p=1}>1的充要條件是M∈△2.

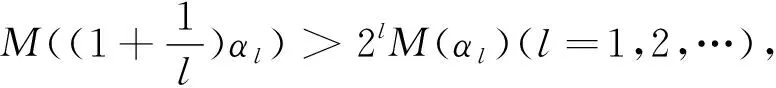
(1)

充分性 若M∈△2,則根據(jù)[5]的定理1.23和[1]的定理1，存在δ>0,使得‖x‖M,p=1蘊含ρM(x)≥δ.因此,對任何x∈S(LM,p),有kx>1所以

定理2 對任何b≥a>0,集合Q={kx∶a≤‖x‖M,p≤b}都為有界集的充要條件是M∈▽2.

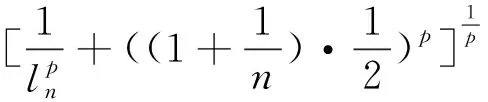
令n→∞,則kn→∞,與已知矛盾.

參考文獻(xiàn)：

[1]段麗芬,崔云安.廣義Orlicz范數(shù)和廣義Luxemburg范數(shù)[J].蘭州理工大學(xué)學(xué)報,2006,32(2):131-134.

[2]ORLICZ W.über Eine Gewisse Klasse Von R?umen Vom Typus B[M].Poland:Bull Acad Polonaise A,1932.

[3]LUXEMBURG W A J.Banach Function Spaces[D].Delft-Netherland:Technische Hogeschoolte Delft,1955.

[4]段麗芬,崔云安.賦廣義Orlicz范數(shù)的Orlicz空間的端點.[J].浙江大學(xué)學(xué)報:理學(xué)版,2007,34(3):252-256.

[5]CHEN S T.Geometry of Orlicz Spaces[M].Warszawa:Dissertations Math,1996.