李洪梅

(泰山學院數(shù)學與系統(tǒng)科學學院,山東泰安 271021)

二階奇異邊值問題正解的存在性

李洪梅

(泰山學院數(shù)學與系統(tǒng)科學學院,山東泰安 271021)

討論奇異邊值問題u"+f(t,u)=0,αu(0)-βu’(0)=0,γu(1)+δu’(1)=0正解的存在性.通過使用錐上的不動點定理得出一個和多個正解的存在性.

奇異邊值問題;正解;不動點定理

0 引言

本文考慮二階奇異邊值問題

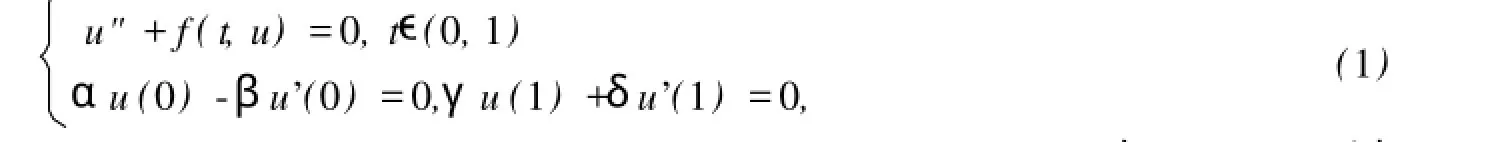
現(xiàn)在這方面的文章相對較多,例如文獻[1-2].其中文獻[1]是利用范數(shù)形式的錐拉伸和壓縮不動點定理得出存在性,文獻[2]在極限條件和可積條件下得出結論.本文利用另外的錐上不動點定理建立了邊值問題存在多個正解的充分條件.我們的結論推廣并豐富了文獻[1-2]的主要結果.

1 預備知識和引理

設E是實Banach空間,P是E中的錐,P導出E中的半序,即:x≤y?y-x∈P.

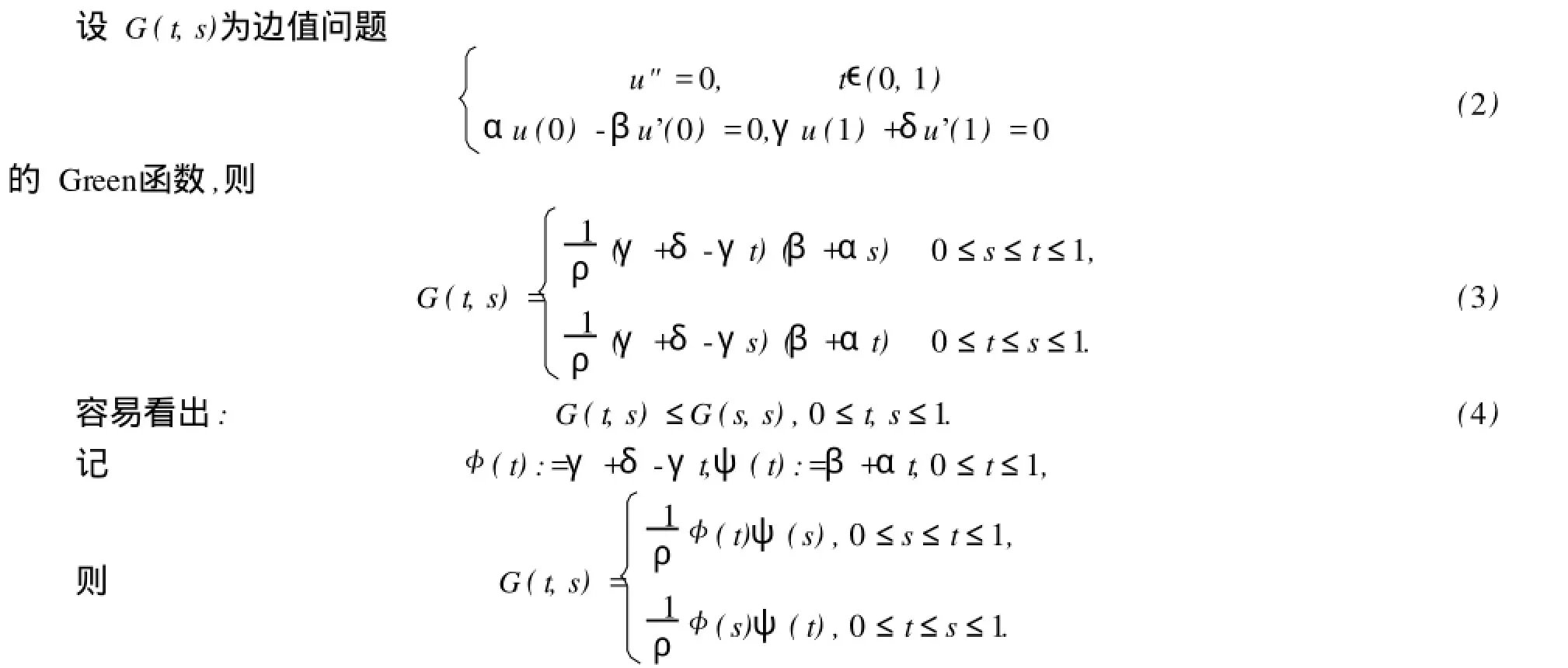
進一步,對t:θ≤t≤1-θ有

引理3[4]設K是實Banach空間E中的錐,是全連續(xù)算子.假定下列條件成立:

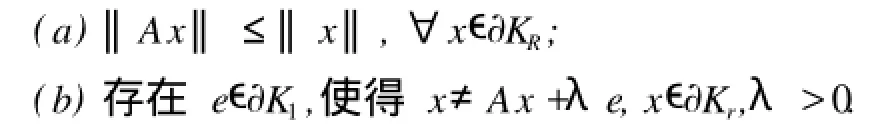
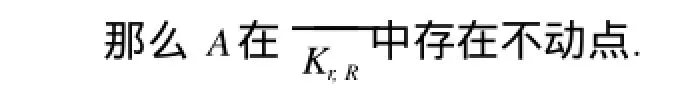
注1 如果(a)在?Kr上成立,且(b)在?KR上成立,則結論仍然成立.

2 正解的存在性

定理1 假設存在兩個不同的正常數(shù)λ和η,使得

那么,邊值問題(1)至少存在一個解u(t)介于λ和η之間.

對(8)式,分兩種情況討論:

注2 推論1包含f是超線性和次線性的情形.

3 多個正解的存在性

定理2 假設存在λ>0,使得條件(h1)成立,且滿足下列條件

故由定理1知,存在兩個解u1,u2,使得0<λ1‖u1‖<λ<‖u2‖<λ2.

定理3 假設存在η>0,使得條件(h2)成立,且滿足條件

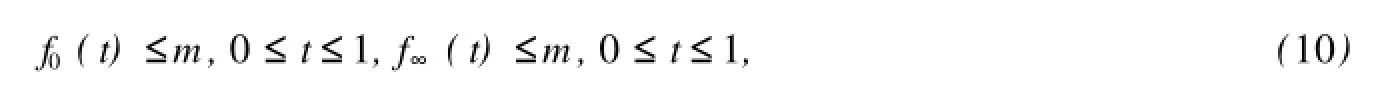
那么邊值問題(1)至少存在兩個解u1,u2,使得0<‖u1‖<η<‖u2‖.

定理4 假設條件(H1),(H2)成立,且存在常數(shù)0<λ1<λ2使得條件(h1)對于λ=λ2(或λ=λ1)成立,條件(h2)對于η=λ1(或η=λ2)成立,那么邊值問題(1)至少存在三個正解u1,u2,u3,滿足

定理3、定理4的證法與定理2,推論1的證法類似,從略.

注3 由定理2-定理4可見,當條件(h1),(h2),(H1),(H2)適當組合,我們可以得到邊值問題(1)存在任意多個正解,具體地說,我們有

定理5 令n=2k+1,k∈N,假設(H1),(H2)成立,并存在常數(shù)0<λ1<λ2<…<λn-1,使得條件(h2) (或(h1))對于λ2i-1,1≤i≤k成立,條件(h1)(或(h2))對于λi2,1≤i≤k成立,那么邊值問題(1)至少存在n個正解u1,u2,…,un,滿足0<‖u1‖<λ1<‖u2‖<λ2<…<‖un-1‖<λn-1<‖un‖.

定理6 令n=2k,k∈N,假設(9),(10)成立,并存在常數(shù)0<λ1<λ2<…<λn-1,使得條件(h1)(或(h2))對于λ2i-1,1≤i≤k成立,條件(h2)(或(h1))對于λ2i,1≤i≤k成立,那么邊值問題(1)至少存在n個正解u1,u2,…,un滿足0<‖u1‖<λ1<‖u2‖<λ2<…<‖un-1‖<λn-1<‖un‖.

[1]馬如云.奇異二階邊值問題的正解[J].數(shù)學學報,1998,41(6):1225-1230.

[2]李仁貴,劉立山.二階奇異非線性微分方程邊值問題的正解[J].應用數(shù)學和力學,2001,22(4):435-440.

[3]JunyuW ang.Theexistenceofpositive solutions for theone-dim ensionalp-lap lacian[J].Proceedingsof theAm ericanM athem aticalSociety,1997,125(8):2275-2283.

[4]Am ann H.Fixed po intequations and nonlinear eigenvalue p roblem s in o rdered Banach spaces[J].SIAM Rev,1976,18(4):620-709.

The Ex istence of Positive Solu tion s for Second O rder Singu lar Boundary Va lue Prob lem s

L IHong-m ei
(Schoo lofM athem atics and System s Science,Taishan University,Tai’an,271021,China)

Thispaper discussed the existence ofpositive so lutions for singu larboundary value p rob lem sof the form u"+f(t,u)=c,αu(0)-βu’(0)=0,γu(1)+δu’(1)=0.Them u ltip licity of positive so lutions is estab lished by using fixed point theorem in cones.

singu lar boundary value p rob lem;positive so lution;fixed point theo rem

O175.8

A

1672-2590(2010)03-0022-04

2010-03-25

李洪梅(1982-),女,山東泰安人,泰山學院數(shù)學與系統(tǒng)科學學院助教.