Optimal Upper and Lower Bounds for Logarithmic Mean*

HOU Shou-w ei ,XU Yan-w u ,CHU Yu-ming

(1.Department of Mathematics,Hangzhou Normal University,Hangzhou 310012,China;2.School of Economics,Shanghai University of Finance and Economic,Shanghai 200433,China;3.Faculty of Science,Huzhou Teachers College,Huzhou 313000,China)

Optimal Upper and Lower Bounds for Logarithmic Mean*

HOU Shou-w ei1,XU Yan-w u2,CHU Yu-ming3

(1.Department of Mathematics,Hangzhou Normal University,Hangzhou 310012,China;2.School of Economics,Shanghai University of Finance and Economic,Shanghai 200433,China;3.Faculty of Science,Huzhou Teachers College,Huzhou 313000,China)

M aking use of elementary differential calculus,we compare the logarithmic mean w ith the convex combination of root-square and harmonic root-squaremeans,and find the greatest valueαand the least valuesβsuch that the double inequalityholds fo r all a,b＞0 w ithare the rootsquare,harmonic root-square,and Logarithmic meansof two positive numbers a and b,w ith a≠b,respectively.

root-squaremean;harmonic root-squaremean;Logarithmic mean

MSC 2000:26E60 26D20

0 In troduction

Fo r p∈R,the p-th pow er mean Mp(a,b)and logarithm ic mean L(a,b)of two positive num bers a and b is defined by respectively.

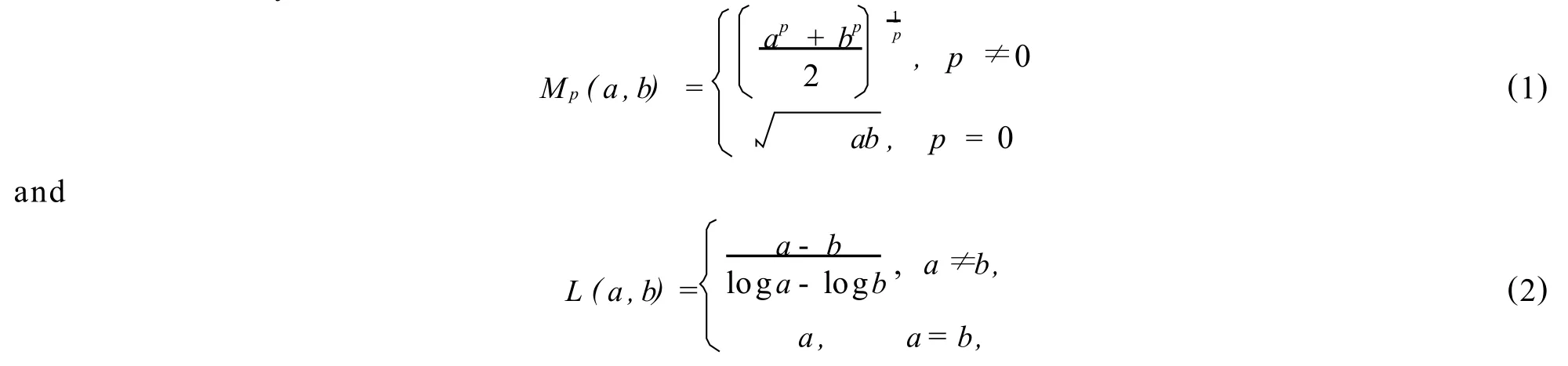
Recently,both mean values have been the subject of intensive research.In particular,many remarkable inequalities for Mp(a,b)and L(a,b)can be found in the literature[1～17].It iswell know n that Mp(a,b)is continuous and strictly increasing w ith respect to p∈R fo r fixed a,b＞0 w ith a≠b,and many means are special cases of the power mean,for examp le,

are the harmonic root-square,harmonic,geometric,arithmetic,and root-square means of a and b,respectively.

Lin[13]p resent the op timal double inequality

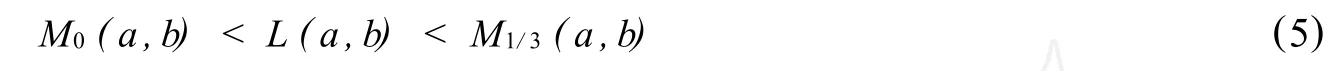
fo r all a,b＞0 w ith a ≠b.

In[6],Long and Chu answer the question:w hat are the greatest value p=p(α,β)and least value q=q(α,β)such that the double inequality

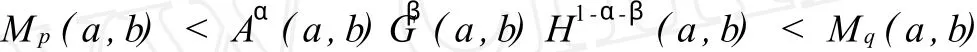
holds fo r all a,b＞0 w ith a≠b andα,β＞0 w ithα+β＜1?

The follow ing sharp bounds for the combination of arithmetic and logarithmic means in term s ofpower mean are given in[7]:

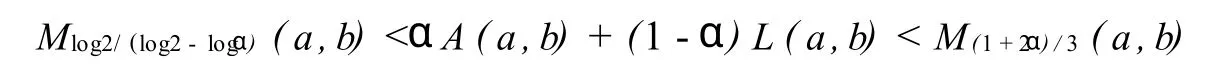
fo r allα∈(0,1)and a,b＞0 w ith a ≠b.

The main purpose of thispaper is to answer the question:w hat are the greatest valueαand least valueβsuch that the double inequality

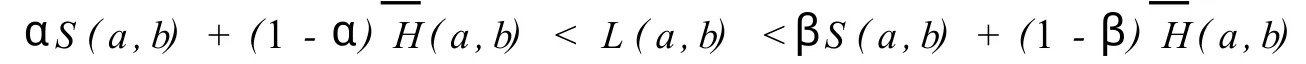
holds fo r all a,b＞0 w ith a≠b.

1 Lemma

In order to establish our main result we need a lemma,w hich we p resent in this section.

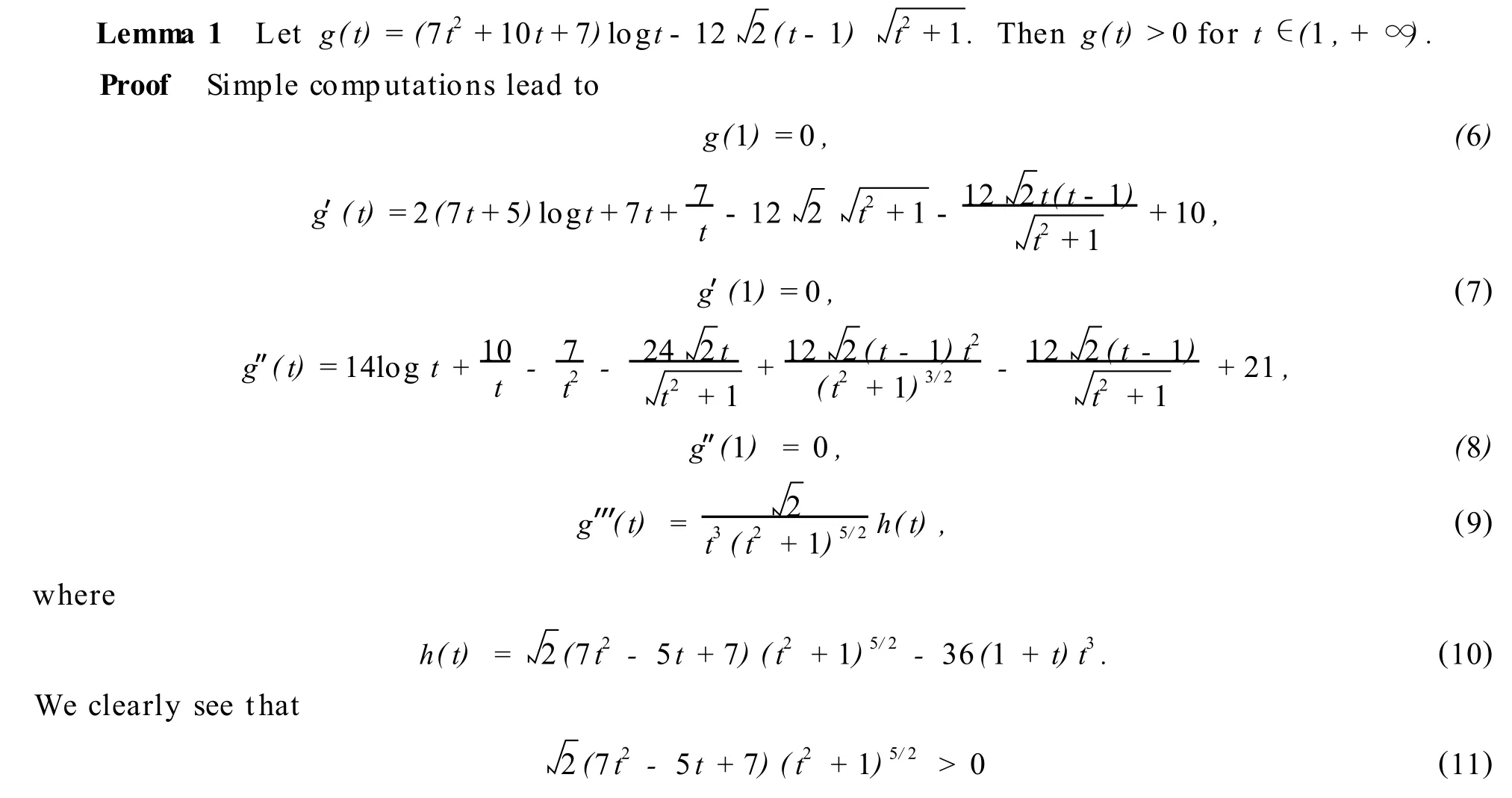
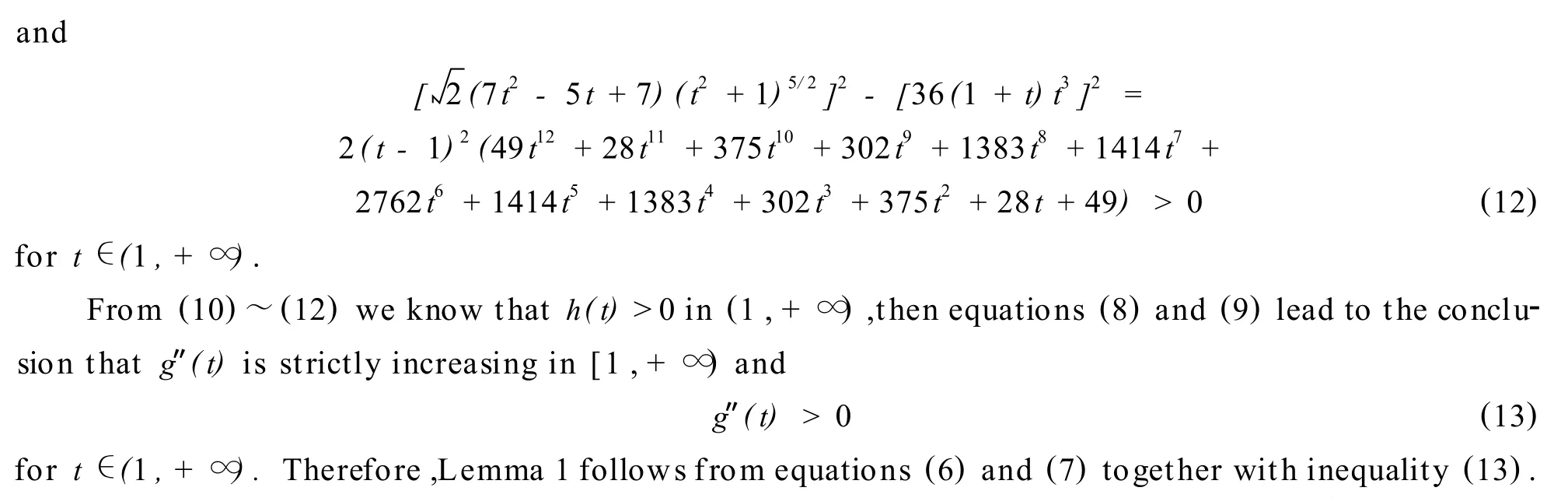
2 Main Result

[1]SH IM Y,CHU Y M,JIANG Y P.Op timal inequalities among varousmeansof two arguments[J].Abstr Appl Anal,2009,2009:1～10.

[2]SH IM Y,CHU Y M,JIANG Y P.Three best inequalities fo r means[J].Int Math Fo rum,2010,5(22):1059～1066.

[3]CHU Y M,XIA W F.Two sharp inequalities fo r powermean,geometricmean,and harmonicmean[J].J Inequal App l,2009,2009:1～6.

[4]CHU YM,XIA W F.Inequalities for generalized logarithmic means[J].J Inequal Appl,2009,2009:1～7.

[5]LONGB Y,CHU Y M.Op timal inequalities for generalized logarithmic,arithmetic,and geometric means[J].J Inequal App l,2010,2010:1～10.

[6]LONGB Y,CHU Y M.Op timal powermean bounds for the weighted geometric mean of classicalmeans[J].J Inequal App l,2010,2010:1～6.

[7]XIA W F,CHU Y M,WANG GD.The op timal upper and lower power mean bounds for a convex combination of the arithmetic and logarithmic means[J].Abstr Appl Anal,2010,2010:1～9.

[8]CHU Y M,LONGB Y.Best possible inequalities between generalized logarithmic mean and classicalmeans[J].Abstr App l Anal,2010,2010:1～13.

[9]CHU Y M,XIA W F.Two op timal double inequalities between power mean and logarithmic mean[J].Comput Math App l,2010,60(1):83～89.

[10]LONGB Y,XIA W F,CHU YM.An op timal inequality for powermean,geometric mean and harmonic mean[J].Int J Mod Math,2010,5(2):149～155.

[11]CHU Y M,Q IU Y F,WANG M K.Sharp power mean bounds fo r the combination of Seiffert and geometric means[J].Abstr Appl Anal,2010,2010:1～12.

[12]Wang M K,Chu Y M,Qiu Y F,et al.An op timal power mean inequality for the comp lete ellip tic integrals[J].App l Math Letters,2011,24:887～890.

[13]L IN T P.The power and the logarithmic mean[J].Amer Math Monthly,1974,81:879～883.

[14]STOLARSKY K B.The power and generalized logarithmic means[J].Amer Math Monthly,1980,87(7):545～548.

[15]IMORU C O.the power mean and the logarithmic mean[J].Internat J Math Math Sci,1982,5(2):337～343.

[16]BURK F.The geometric,logarithmic,and arithmetic mean inequality[J].Amer Math Monthly,1987,94(6):527～528.

[17]ALZER H,Q IU SL.Inequalities for means in two variables[J].A rch Math,2003,80(2):201～215.

MSC 2000:26E60 26D20

對(duì)數(shù)平均的最佳上下界

候守偉1,徐言午2,褚玉明3

(1.杭州師范大學(xué)數(shù)學(xué)系,浙江杭州310012;2.上海財(cái)經(jīng)大學(xué)經(jīng)濟(jì)學(xué)院,上海200433;3.湖州師范學(xué)院理學(xué)院,浙江湖州 313000)

利用初等微分學(xué)比較了對(duì)數(shù)平均與平方根平均和調(diào)和平方根平均的凸組合,發(fā)現(xiàn)了使得雙向不等式αS(a,b)+(1對(duì)所有 a,b＞0且 a≠b成立的α的最大值和β的最小值,其中 S(a,b)分別表示二個(gè)正數(shù) a與b的平方根平均、調(diào)和平方根平均和對(duì)數(shù)平均.

平方根平均;調(diào)和平方根平均;對(duì)數(shù)平均

O174.1

O174.1 Document code:A Article ID:1009-1734(2011)01-0007-04

date:2011-01-21

s:This research is suppo rted by the Natural Science Foundation of China(11071067)and the Innovation Team Foundation of the Department of Education of Zhejiang Porvince(T200924).

Biography:Hou Shou-wei,Postgraduate student of grade 2009,Department of Mathematics,Hangzhou Normal U-niversity,Research Interest:Comp lex Analysis.