Ostrowski定理的推廣與非奇異H-矩陣的實(shí)用判定
韓貴春,錢茜,張俊麗
(1.內(nèi)蒙古民族大學(xué)數(shù)學(xué)學(xué)院,內(nèi)蒙古通遼 028043;2.電子科技大學(xué)成都學(xué)院文理系,四川成都 611731)
Ostrowski定理的推廣與非奇異H-矩陣的實(shí)用判定
韓貴春1,錢茜2,張俊麗1
(1.內(nèi)蒙古民族大學(xué)數(shù)學(xué)學(xué)院,內(nèi)蒙古通遼 028043;2.電子科技大學(xué)成都學(xué)院文理系,四川成都 611731)
利用α2-雙對角占優(yōu)理論,給出了幾個(gè)判定非奇異H-矩陣的充分條件,擴(kuò)大了非奇異H-矩陣的判定范圍,并給出了相應(yīng)的數(shù)值算例說明結(jié)果的有效性.
非奇異H-矩陣;雙對角占優(yōu)矩陣;非零元素鏈
1 引言


2 預(yù)備知識(shí)

3 主要結(jié)果






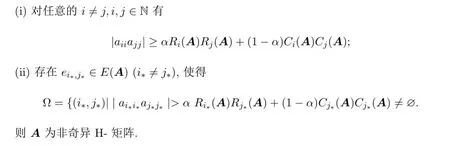
[1]Huang T Z,Li W,Lei G Y.Contributions to Nonsingular H-matrices[J].ZAMM Z.Angew.Math.Mech., 2000,80(1):493-496.
[2]孫玉祥.廣義對角占優(yōu)矩陣的充分條件[J].高等學(xué)校計(jì)算數(shù)學(xué)學(xué)報(bào),1997,19(3):216-223.
[3]Sun Y.An improvement on a theorem by Ostrowski and its applications[J].Northeast Math,1991,7(4):497-502.
[4]黃廷祝.Ostrowski定理的推廣與非奇異矩陣的條件[J].計(jì)算數(shù)學(xué),1994,16(1):19-24.
[5]沈光星.連對角占優(yōu)矩陣的一些性質(zhì)[J].計(jì)算數(shù)學(xué),1990,12(2):132-135.
[6]宋乾坤.廣義嚴(yán)格對角占優(yōu)矩陣與M-矩陣的充分判據(jù)[J].高等學(xué)校計(jì)算數(shù)學(xué)學(xué)報(bào),2004,26(4):298-305.
[7]房秀芬,黃廷祝.α-雙對角占優(yōu)矩陣與M-矩陣的刻畫[J].工程數(shù)學(xué)學(xué)報(bào),2005,22(1):123-127.
[8]李敏,孫玉祥.α-對角占優(yōu)矩陣的討論及其應(yīng)用[J].工程數(shù)學(xué)學(xué)報(bào),2009,26(5):941-945.
[9]郭微,孫玉祥.H-矩陣的實(shí)用判定[J].工程數(shù)學(xué)學(xué)報(bào),2010,27(2):347-352.
[10]徐成賢,徐宗本.矩陣分析[M].西安:西北工業(yè)大學(xué)出版社,1991.
[11]黃政.非奇異H-矩陣的一組充分條件[J].吉首大學(xué)學(xué)報(bào),2006,27(3):12-14.
[12]程云鵬,張凱院,徐仲.矩陣論[M].2版.西安:西北工業(yè)大學(xué)出版社,1991.
[13]李陽,宋岱山,路永潔.α-雙對角占優(yōu)與非奇異H-矩陣的判定[J].合肥工業(yè)大學(xué)學(xué)報(bào),2005,28(12):1624-1626.
Generalizations Ostrowski′s theorem and practical criteria for H-matrices
Han Guichun1,Qian Qian2,Zhang Junli1
(1.School of Mathematics,Inner Mongolia University for the Nationalities,Tongliao028043,China;
2.Department of Arts and Science,College of University of Electronic Science and Technology of China, Chengdu611731,China)
In this paper,we give some sufcient conditions for nonsingular H-matrices by the theory of α2-double diagonally dominant matrices.The criteria for nonsingular H-matrices are expended,and efectiveness of the criteria is illustrated by numerical examples.
nonsingular H-matrix,double diagonally dominant matrix,chain of nonzero elements
O151.21
A
1008-5513(2013)06-0601-08
10.3969/j.issn.1008-5513.2013.06.008
2012-12-05.
內(nèi)蒙古民族大學(xué)科學(xué)研究基金(NMD1226).
韓貴春(1978-),碩士,講師,研究方向:數(shù)值代數(shù).
2010 MSC:15A57

