汪賢華

(北京石油化工學(xué)院數(shù)理系,北京 102617)

局部θ-連通空間的幾個(gè)性質(zhì)

汪賢華

(北京石油化工學(xué)院數(shù)理系,北京 102617)

拓?fù)淇臻g;連通空間;θ-連通空間;局部θ-連通空間;θ-連通分支

DO I：10.3969/j.issn.1008-5513.2013.04.005

1 引言

連通空間是拓?fù)淇臻g中一類非常重要的拓?fù)淇臻g[1],它是用分離集來(lái)定義的,即拓?fù)淇臻gX稱為連通的是指如果X不能表示為兩個(gè)非空的分離子集的并集.對(duì)連通空間的研究是一般拓?fù)鋵W(xué)研究的一個(gè)重要課題,文獻(xiàn)[2]研究了δ-連通空間.文獻(xiàn)[3]研究了θ-連通空間及其相關(guān)的一些性質(zhì),隨后文獻(xiàn)[4-5]對(duì)局部θ-連通空間和弱θ-連通空間做了一些相關(guān)的研究,本文在此基礎(chǔ)上進(jìn)一步討論了局部θ-連通空間的充要條件,并研究了在商映射下的不變性,最后討論了局部θ-連通空間的可和性與可積性,從而進(jìn)一步完善了θ-連通空間及θ-連通性等理論.

2 基本定義

假設(shè)(X,τ(X))是一拓?fù)淇臻g,A是X的子集,C lX(A)表示A在X中的閉包.文中未給出的定義請(qǐng)參閱文獻(xiàn)[1].在文獻(xiàn)[6-7]中,關(guān)于θ-閉集的定義如下:

定義1[6-7]拓?fù)淇臻gX的子集A稱為X的θ-閉集是指如果對(duì)于任意的p∈XA,都存在U∈τ(X),使得

類似于閉包的定義,有下面的定義:

定義2[3]假設(shè)A是拓?fù)淇臻gX的子集,稱x∈X是A的θ-聚點(diǎn)是指如果對(duì)任意的包含x的U∈τ(X),都有

定義3[3]假設(shè)A是拓?fù)淇臻gX的子集,集A的一切θ-聚點(diǎn)構(gòu)成的集合稱為A的θ-閉包,記作[A]θ.

定義4[3]拓?fù)淇臻gX的子集P,Q稱為θ-分離的是指

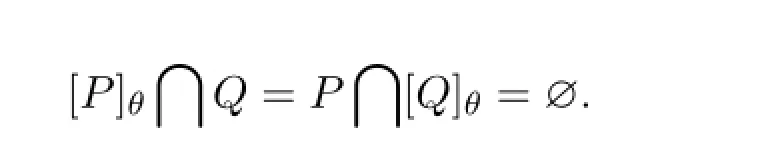
定義5[3]設(shè)X是一拓?fù)淇臻g,如果X不能表示為兩個(gè)非空的θ-分離子集的并集,則稱X是θ-連通空間.設(shè)S是X的子集,如果S作為子空間是θ-連通的,則稱S是X的θ-連通子集.

定義6[4-5]設(shè)x是拓?fù)淇臻gX中的一點(diǎn),如果對(duì)X中任意包含x的開(kāi)集U,都存在X中的一個(gè)θ-連通的開(kāi)集V,滿足x∈V?U,則稱X在x點(diǎn)處是局部θ-連通的.若X在每一點(diǎn)處都是局部θ-連通的,則稱X是一個(gè)局部θ-連通空間.若拓?fù)淇臻gX的子集Y作為X的子空間是局部θ-連通的,則稱Y是X的局部θ-連通子集.

定義7[5]設(shè)(X,τ(X))是一拓?fù)淇臻g,B是τ的一個(gè)基,若B中每一個(gè)元素都是θ-連通的,則稱B為X的θ-連通基.

定義8[3]拓?fù)淇臻gX的一個(gè)子集稱為X的θ-連通分支是指如果它是θ-連通的,并且不是X其它θ-連通子集的真子集.

3 主要結(jié)論

在文獻(xiàn)[3]中,得到了性質(zhì):設(shè)A是拓?fù)淇臻gX的子集,如果A是連通的,則A一定是θ-連通的.也就是θ-連通空間是比連通空間更廣泛的一類空間.在文獻(xiàn)[5]中作者證明了局部連通空間是局部θ-連通空間.說(shuō)明局部θ-連通空間是比局部連通空間更廣泛的一類空間.

局部連通性對(duì)于開(kāi)子集有遺傳性,在局部θ-連通空間中,對(duì)于開(kāi)子集也有:

定理1若X是局部θ-連通空間,A?X是X的開(kāi)子集,則A是局部θ-連通空間.

證明對(duì)于A中的任意一點(diǎn)x,設(shè)U是A中包含x的任意開(kāi)集,則由于A是X的開(kāi)子集,所以U也是X的開(kāi)集,x∈U,再由X是局部θ-連通空間,故存在X中的θ-連通開(kāi)集W,使得:x∈W?U,而W?A,A是X的開(kāi)子集,所以W亦是A中的θ-連通開(kāi)集,因此A是局部θ-連通空間.

定理2局部θ-連通空間的θ-連通分支是開(kāi)集.

證明設(shè)X是局部θ-連通空間,A是X的θ-連通分支.對(duì)于任意的x∈A,x有一個(gè)θ-連通鄰域,它也必含在A中,所以x是A的內(nèi)點(diǎn),因此A是開(kāi)集,即局部θ-連通空間的θ-連通分支是開(kāi)集.

定理3設(shè)(X,τ(X))是一拓?fù)淇臻g,則下列命題等價(jià):

(1)X是局部θ-連通空間;

(2)X的任意開(kāi)集的任意θ-連通分支都是開(kāi)集;

(3)X有一個(gè)θ-連通基;

(4)對(duì)于任意的x∈X,x有一個(gè)θ-連通的鄰域基B(x).

證明(1)?(2)?(3)見(jiàn)文獻(xiàn)[4]定理2.

(3)?(4)設(shè)X有一個(gè)θ-連通基B,則對(duì)于任意x∈X,令

由于連通基B中每一元素都是θ-連通的,故B(x)就是x的一個(gè)θ-連通的鄰域基.

(4)?(1)假設(shè)對(duì)于任意的x∈X,x有一個(gè)θ-連通的鄰域基B(x),U是X中包含x的任意開(kāi)集,則由鄰域基的定義存在θ-連通開(kāi)集V∈B(x),使得x∈V,令Vx≡U∩V,則Vx是θ-連通的,且x∈Vx?U,所以X是局部θ-連通空間.

對(duì)于局部連通空間,在商映射下是保持不變的,對(duì)于局部θ-連通空間同樣也有:

定理4設(shè)f:X1→X2為商映射,若X1是局部θ-連通空間,則X2也是局部θ-連通空間.

證明設(shè)A是X2中的任意開(kāi)集,B是A的θ-連通分支,由定理3知,只需證明B是開(kāi)集即可.設(shè)x∈f-1(B),則x∈f-1(A)=U,由于f是商映射,故U是開(kāi)集.設(shè)K是U的θ-連通分支,由于X1是局部θ-連通空間,故x∈K?U,K是θ-連通的開(kāi)集,f(K)是θ-連通的,且f(x)∈f(K),由f(x)∈B知f(K)∩B/=?,故f(K)∪B是A中的θ-連通子集,因此

所以x∈K?f-1(B),也就是f-1(B)是開(kāi)集,再由f是商映射,則B是開(kāi)集,故X2也是局部θ-連通空間.

推論1設(shè)f:X1→X2是連續(xù)且滿的開(kāi)(或閉)映射,若X1是局部θ-連通空間,則X2也是局部θ-連通空間.

在文獻(xiàn)[1]中有,局部連通空間具有可和性,對(duì)于局部θ-連通空間的可和性,同樣也有下面的定理:

定理5設(shè)A是一指標(biāo)集,{Xα}α∈A是一組兩兩不相交的拓?fù)淇臻g族,則和空間

是局部θ-連通空間當(dāng)且僅當(dāng)對(duì)任意α∈A,Xα是局部θ-連通空間.

證明令

充分性設(shè)對(duì)任意α∈A,Xα是局部θ-連通空間.任給x∈X,U為X中任意包含x的開(kāi)集,則存在α0∈A使得x∈Xα0,則U∩Xα0即為Xα0中的開(kāi)集.而Xα0是局部θ-連通空

間,故存在Xα0中的θ-連通開(kāi)集V,使得:

由Xα0是X中的開(kāi)集,易知V也是X中的θ-連通開(kāi)集,所以:

是局部θ-連通空間.

必要性設(shè)X是局部θ-連通空間.對(duì)任意α∈A,設(shè)x∈Xα,U為Xα中包含x的任意開(kāi)集,則x∈X,且U亦是X中包含x的開(kāi)集,由于X是局部θ-連通空間,故存在X中的θ-連通開(kāi)集V,使得:x∈V?U,而Xα是X的既開(kāi)又閉的子空間,所以V亦是Xα中的θ-連通開(kāi)集.即:Xα是局部θ-連通空間.

即局部θ-連通空間也具有可和性.

對(duì)于可積性,也有類似于局部連通空間的性質(zhì):

定理6設(shè)S是一指標(biāo)集,對(duì)于任意的s∈S,Xs是非空的,則乘積空間

是局部θ-連通空間當(dāng)且僅當(dāng)對(duì)于任意的s∈S,Xs是局部θ-連通空間,且除了有限個(gè)以外還是θ-連通空間.

證明充分性假設(shè)對(duì)于任意的s∈S,Xs是局部θ-連通空間,且當(dāng)s∈S{s1,s2,…,sn},Xs是θ-連通空間.當(dāng)s/∈S{s1,s2,…,sn},由于Xs是局部θ-連通空間,故由定理3知Xs有一個(gè)θ-連通基Bs,令

其中當(dāng)s/∈S{s1,s2,…,sn}時(shí),Ws∈Bs,當(dāng)s∈S{s1,s2,…,sn}時(shí),Ws=Xs,則B是X的一個(gè)θ-連通基,由定理3知積空間

是局部θ-連通空間.

必要性假設(shè)積空間

是局部θ-連通空間,則對(duì)于任意的s∈S,ps:X→Xs是投影映射,則每個(gè)ps都是連續(xù)開(kāi)映射,由推論1可得對(duì)于任意的s∈S,Xs是局部θ-連通空間.

現(xiàn)取任意x∈X,由X是局部θ-連通空間,設(shè)U是包含x的θ-連通開(kāi)集,于是存在積拓?fù)渲械幕?/p>

其中s∈S{s1,s2,…,sn}時(shí),Ys=Xs,使得

于是當(dāng)s∈S{s1,s2,…,sn}時(shí),ps(U)?Ys=Xs,故Xs=ps(U)是θ-連通空間.

推論2[4]若X1,X2,…,Xn都是局部θ-連通空間,則X=X1×X2×…×Xn也是局部θ-連通空間.

通過(guò)以上的研究,不難發(fā)現(xiàn)局部θ-連通空間與局部連通空間有著非常類似的拓?fù)湫再|(zhì),對(duì)于局部連通空間的其他一些性質(zhì),例如和緊空間有關(guān)的性質(zhì),是否也可以推廣到局部θ-連通空間還有待于進(jìn)一步的研究.

[1]Engelking R.General Topology[M].Warszawa:PWN,1977.

[2]汪賢華.δ-連通空間[J].純粹數(shù)學(xué)與應(yīng)用數(shù)學(xué),2004,20(3):243-247.

[3]汪賢華,高汝林.θ-連通空間及其性質(zhì)[J].北京石油化工學(xué)院學(xué)報(bào),2005,13(1):61-64.

[4]姜金平,王小霞.局部θ-連通空間[J].江西科學(xué),2008,26(1):11-12.

[5]姜金平,王小霞.弱θ-連通空間及其性質(zhì)[J].西南民族大學(xué)學(xué)報(bào):自然科學(xué)版,2008,34(1):36-38.

[6]D ikran jan D,G iu li E.S(n)-θ-closed spaces[J].Top.and its A pp l.,1988(28):59-74.

[7]Filippo Cammaroto,G iovanni Lo Faro,Jack Porter R.N-Sets and near com pact spaces[J].Bollettino U.M.I,1999,(8,2-B):291-298

The several p roperties of localθ-connected space

Wang Xianhua
(Department of Mathematics and Physics,Beijing Institute of Petrochem ical Technology, Beijing 102617,China)

topological space,connected space,θ-connected space,localθ-connected space,θ-com ponent 2010 M SC:54D 05,54B10

O189.11

A

1008-5513(2013)04-0359-05

2013-05-09.

北京市教育委員會(huì)科技計(jì)劃面上項(xiàng)目(Z2011-008).

汪賢華(1977-),碩士,講師,研究方向：一般拓?fù)鋵W(xué).