薛豐剛,丁丹平

(江蘇大學(xué)理學(xué)院數(shù)學(xué)系,江蘇鎮(zhèn)江 212013)

高階Cam assa-H olm方程的一類(lèi)行波解

薛豐剛,丁丹平

(江蘇大學(xué)理學(xué)院數(shù)學(xué)系,江蘇鎮(zhèn)江 212013)

研究高階Camassa-Holm方程的行波解,采用一種新的方法求解行波方程,獲得了高階Cam assa-Holm方程的一類(lèi)行波解.

高階Cam assa-Holm方程;行波方程;行波解

DO I：10.3969/j.issn.1008-5513.2013.04.009

1 引言

2003 年,文獻(xiàn)[1]首先得到了這個(gè)高階Cam assa-Holm方程.具體形式如下:

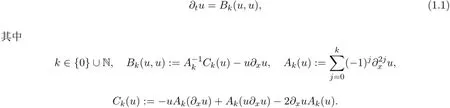
2009 年,文獻(xiàn)[2]研究了高階Cam assa-Holm方程的全局適定性,得到了一個(gè)弱解.

2010 年,文獻(xiàn)[3]研究高階Camassa-Holm方程全局解的存在性.通過(guò)對(duì)局部頻率方程采用小粘度方法確定了全局解.特別是全局解在給定的有限數(shù)值范圍內(nèi)是能量守恒的;文獻(xiàn)[4]利用Kato定理證明了高階Camassa-Holm方程解的存在唯一性及連續(xù)性的局部適定性定理,得到了方程的守恒量和解的先驗(yàn)估計(jì),在此基礎(chǔ)上得到了解的整體存在性.

本文主要研究高階Cam assa-Holm行波方程,給出了行波解的具體表達(dá).第二節(jié)介紹高階Camassa-Holm行波方程的形式解;第三節(jié)討論形式解的能量守恒;第四節(jié)給出本文的主要定理及證明.

2 高階Cam assa-Holm行波方程的形式解

3 形式解的能量守恒

4 行波解

附錄A.1

附錄A.2

附錄A.3

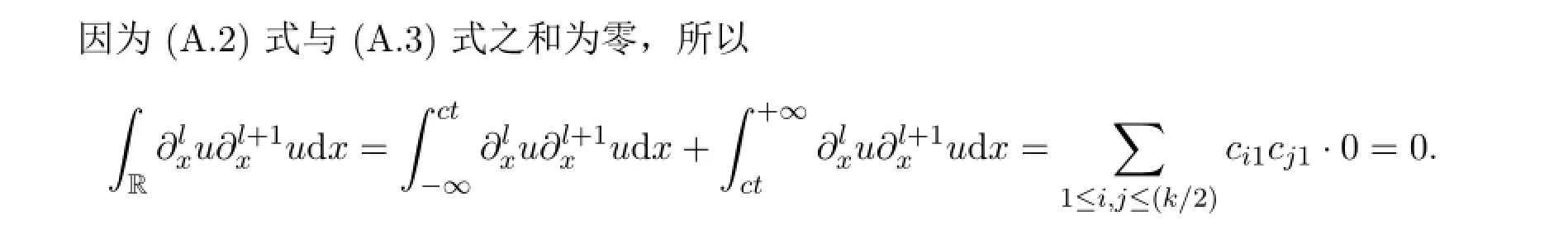
[1]Constantin A,Kolev B.Geodesic fow on the d if eom orphism group of the circle[J].Comm ent.M ath.Helv., 2003,78(4):787-804.

[2]Coclite G M,Holden H,Karlsen K H.Well-posedness of higher-order Camassa-Holm equations[J].Journal of Dif erential Equations,2009,246:929-963.

[3]D ing Danp ing,L¨u Peng.Conservative solu tions for higher-order Cam assa-Holm equations[J].J.M ath. Phys.,2010,51(7):323-327.

[4]張榀.一類(lèi)高階淺水波方程的適定性和爆破理論[D].鎮(zhèn)江:江蘇大學(xué)圖書(shū)館,2010.

[5]Temam R.In f nite Dimensional Dynam ical System s in M echanical and Physics[M].New York:Sp ringer Verlag,1997.

[6]謝元喜,唐駕時(shí).求一類(lèi)非線性偏微分方程解析解的一種簡(jiǎn)潔方法[J].物理學(xué)報(bào),2004,53(9):2828-2830.

[7]祁新雷,李金花.(1+1)維Burgers方程新的行波解[J].純粹數(shù)學(xué)與應(yīng)用數(shù)學(xué),2008,24(4):90-93.

[8]Cam assa R,Holm D D.An integrab le shallow water equation w ith peaked solu tions[J].Phys.Rev.Lett., 1993,71:1661-1664.

[9]楊宗培.實(shí)系數(shù)一元偶次代數(shù)方程無(wú)實(shí)根的判別法則[J].南昌大學(xué)學(xué)報(bào):工科版,1982,4(1):43-49.

[10]韓永東.關(guān)于倒數(shù)方程的解法的探究[J].吉林廣播電視大學(xué)學(xué)報(bào),2011,09:24-25.

[11]安敏,彭亞綿.數(shù)學(xué)中特殊高次方程的解法研究[J].科技信息,2007,12:134-135.

[12]尚德泉.一種求高次代數(shù)方程全部根的矩陣方法[J].數(shù)學(xué)教學(xué)研究,2009,28(5):57-58.

A type of travelling w ave solu tions of h igher-order Cam assa-Holm equations

Xue Fenggang,Ding Danping

(College of Sciences,Jiangsu University,Zhen jiang 212013,China)

This paper researches the travelling wave solutions of higher-order Cam assa-Holm equations.A new method is used to solve the travelling wave equation,and a type of travelling wave solutions are obtained.

higher-order Camassa-Holm equations,travelling wave equation,travelling wave solutions

O175.29

A

1008-5513(2013)04-0387-10

2013-04-19.

薛豐剛(1980-),碩士生,研究方向：非線性偏微分方程.

2010 M SC:35A05