關(guān)于廣義齊性Cochrane和的加權(quán)均值

白文,任剛練

(1.西北大學(xué)數(shù)學(xué)系,陜西西安 710069;2.咸陽(yáng)師范學(xué)院數(shù)學(xué)與信息科學(xué)學(xué)院,陜西咸陽(yáng) 712000)

關(guān)于廣義齊性Cochrane和的加權(quán)均值

白文1,任剛練2

(1.西北大學(xué)數(shù)學(xué)系,陜西西安 710069;2.咸陽(yáng)師范學(xué)院數(shù)學(xué)與信息科學(xué)學(xué)院,陜西咸陽(yáng) 712000)

研究了廣義齊性Cochrane和的一些加權(quán)均值,并利用不完全區(qū)間上特征和的性質(zhì),Dirichlet函數(shù)的均值估計(jì)以及周期Bernoulli多項(xiàng)式的性質(zhì),得到一些較強(qiáng)的漸近公式.

廣義齊性Cochrane和;周期Bernoulli多項(xiàng)式;Dirichlet L-函數(shù);特征和

1 引言及定理

2000年,Todd Cochrane引入下面的和式[1]:

十分類(lèi)似,許多作者對(duì)它作了深入研究并獲得許多優(yōu)美的結(jié)果.

2 幾個(gè)引理

為了完成定理的證明,需要以下幾個(gè)引理:

引理1令m為任意給定常數(shù),n為非負(fù)整數(shù),p為素?cái)?shù).對(duì)于模p的任意奇特征χ,即χ(-1)=-1,則有

3 定理的證明

現(xiàn)在來(lái)完成定理的證明.

根據(jù)引理2,引理4可得

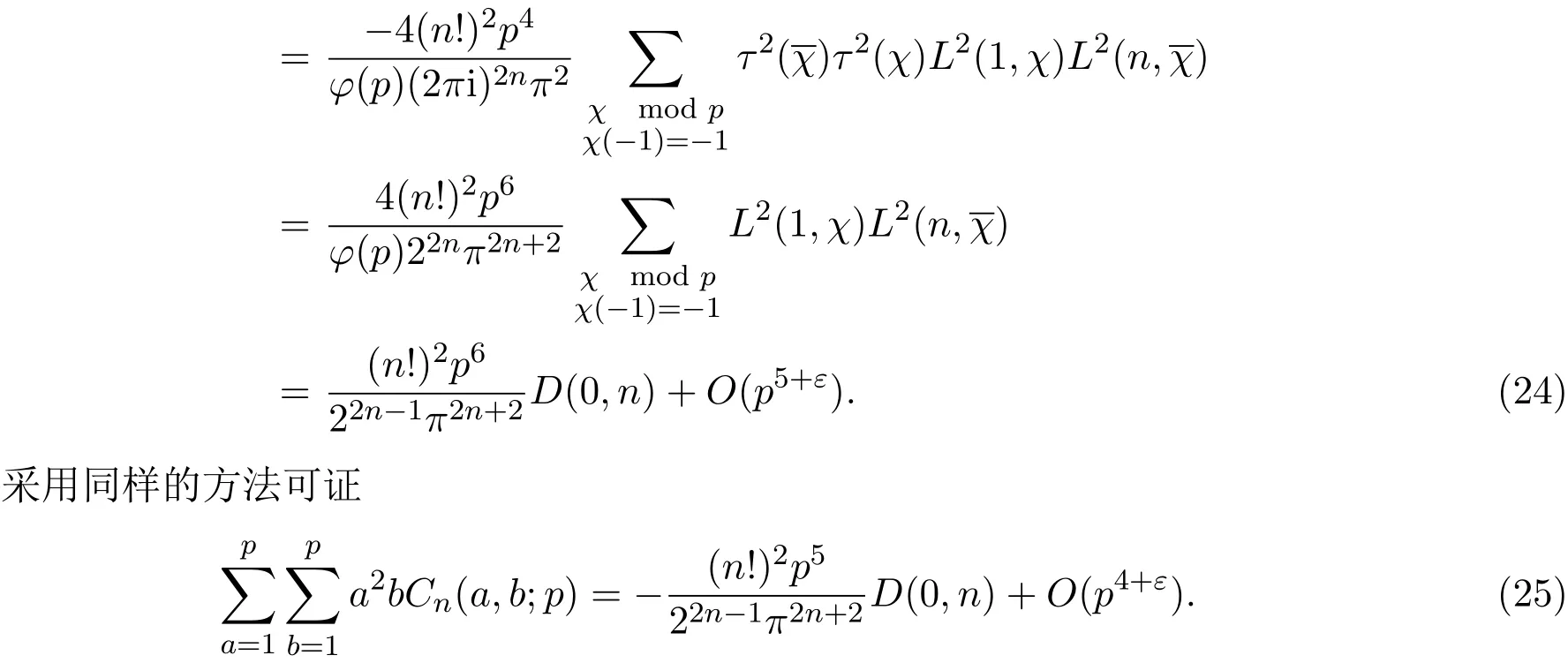
這樣就完成定理2的證明.由(24)式和(25)式可得出推論.

[1]徐哲峰,張文鵬.Dirichlet特征及其應(yīng)用[M].北京:科學(xué)出版社,2008.

[2]Zhang Wenpeng.On a sum analogous to Dedekind sum and its mean square value formula[J].International Journal of Mathematics and Mathematical Sciences,2002,32(1):47-55.

[3]Xu Zhefeng.A mean value of Cochrane sum[J].Acta Mathematica Sinica,2009,25(2):223-234.

[4]Liu Hongyan,Zhang Wenpeng.On a generalized cochrane sum and its hybrid mean value formula[J].The Ramanujan Journal,2005,9(3):373-380.

[5]任剛練,白文.廣義Cochrane和在四分之一區(qū)間上的分布[J].內(nèi)蒙古師范大學(xué)學(xué)報(bào),2013,42(1):1-4.

[6]Xu Zhefeng.A note on the 2k-th power mean of character sums over the quarter interval[J].Proceedings of American Mathematical Society,2008,136:4175-4184.

[7]Toyoizumi M.On certain character sums[J].Acta.Arithmeica,1990,55:229-232.

[8]Zhang Wenpeng,Yi Yuan,He Xiali.On the 2k-th power mean of Dirichlet L-functions with the weight of general Kloosterman sums[J].Journal of Number Theory,2000,84:199-213.

On the weighted mean of generalized homogeneous Cochrane sum

Bai Wen1,Ren Ganglian2
(1.Department of Mathematics,Northwest University,Xi′an710069,China; 2.College of Mathematics and Information Science,Xianyang Normal University,Xianyang712000,China)

The weighted mean of generalized homogeneous Cochrane sum is studied.By using the properties of character sum over the incomplete intervals,mean value estimate of Dirichlet L-functions,and the periodic Bernoulli polynomial,some related asymptotic formulas are obtained.

generalized homogeneous Cochrane sum,periodic Bernoulli polynomial,L-functions, character sum

O156.2

A

1008-5513(2013)02-0190-07

10.3969/j.issn.1008-5513.2013.02.013

2012-12-10.

國(guó)家自然科學(xué)基金(2009JQ1009);陜西省教育廳自然科學(xué)專(zhuān)項(xiàng)基金(09JK803).

白文(1986-),碩士生,研究方向：數(shù)論.

2010 MSC:11N05