朱偉杰,劉素英,趙凱,江修田

(青島大學數(shù)學科學學院,山東青島 266071)

一類奇異積分算子的加權估計

朱偉杰,劉素英,趙凱,江修田

(青島大學數(shù)學科學學院,山東青島 266071)

假設A是一個Young函數(shù),M#D為廣義sharp極大函數(shù).本文首先引進了LA-H¨ormander條件,對于滿足LA-H¨ormander條件的算子T,得到了與T相關的廣義sharp極大函數(shù)的估計.然后,再利用該估計得到了算子T的加權Lp范數(shù)被Hardy-Littlewood極大函數(shù)和與ˉA相關的極大函數(shù)的加權Lp范數(shù)所控制(0＜p＜∞).

sharp極大函數(shù);Young函數(shù);Hardy-Littlewood極大函數(shù);奇異積分算子

1 引言

眾所周知,奇異積分算子在調(diào)和分析中起著非常重要的作用,并得到了廣泛的研究.1970年,文獻[1]研究了經(jīng)典奇異積分算子的Lp估計.1972年,文獻[2]得到了經(jīng)典奇異積分算子的加權Lp估計,即:對于0＜p＜∞和ω∈A∞,T的加權Lp范數(shù)被Hardy-Littlewood極大函數(shù)的加權Lp范數(shù)所控制.1989年,文獻[3]研究了光滑面積函數(shù)的加權范數(shù)不等式及加權Sobolev不等式.1997年,文獻[4]證明了1＜p≤∞時線性及非線性的奇異積分算子交換子的sharp加權估計.文獻[5]證明了分數(shù)次Orlicz極大算子在齊型空間中的局部加權端點估計.2005年,文獻[6]對于經(jīng)典奇異積分算子T的核引進了LA-H¨ormander條件,在該條件下得到了算子T的加權Lp范數(shù)被與相關的極大函數(shù)的加權Lp范數(shù)所控制(0＜p＜∞).文獻[7]引進了廣義sharp極大函數(shù),得到了類似于經(jīng)典sharp極大函數(shù)的Fefferman-Stein估計.

自然地,可以考慮具有非光滑核的奇異積分算子的類似問題,這里研究了文獻[8]中的在L2上有界的具有非光滑核的奇異積分算子的加權估計.首先引進了非光滑核所滿足的LA-H¨ormander條件,得到估計

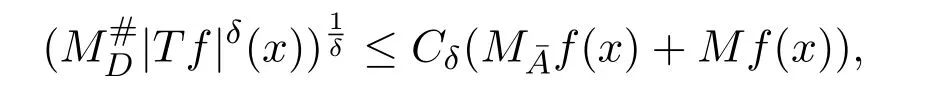
2 預備知識

定義2.1[7]若對集合X賦予距離d及非負Borel測度μ,且對x∈X和r＞0,μ滿足雙倍條件:

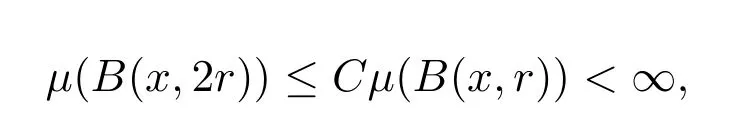
其中B(x,r)={y∈X:d(x,y)＜r},則稱(X,d,μ)為齊型空間.

由雙倍條件可得,對x,y∈X和r＞0,存在cμ≥1和0≤N≤n,使得

3 主要結(jié)果及其證明

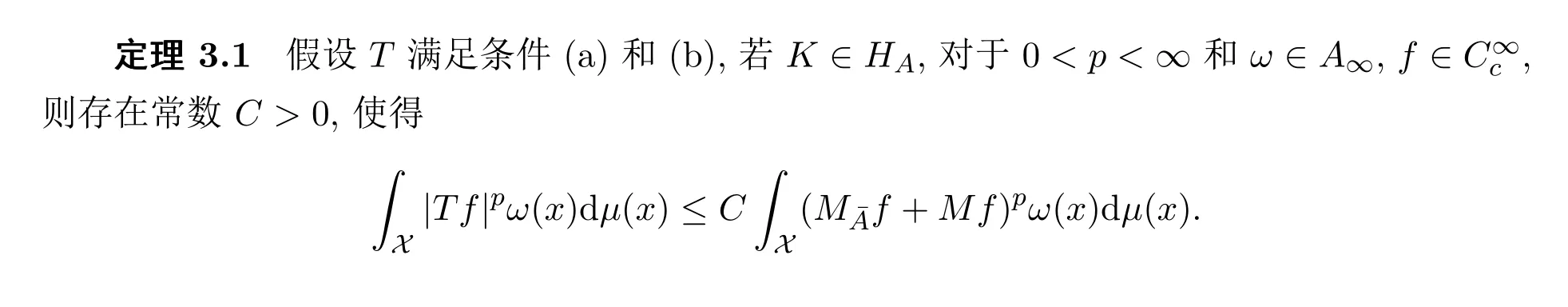
[1]Stein E M.Singular Integral and Diffrentiability Properties of Functions[M].Princeton:Princeton Univ. Press,1970.

[2]Coifman R.Distribution function inequalities for singular integrals[J].Proc.Natl.Acad.Sci.,1972,69(10): 2838-2839.

[3]Wilson J M.Weighted norm inequalities for the continuos square functions[J].Trans.Amer.Math.Soc., 1989,314(2):661-692.

[4]P′erez C.Sharp estimates for commutators of singular integrals via iterations of the Hardy-Littlewood Maximal functin[J].Fourier Anal.Appl.,1997,3(6):74-756.

[5]田茂茜.分數(shù)次Orlicz極大算子在齊型空間中的局部加權端點估計[J].純粹數(shù)學與應用數(shù)學,2011,27(5): 622-627.

[6]Lorente M,Riveros M S,de la Torre A.Weighted estimates for singular integral operators satisfying H¨ormander conditions of Young type[J].Fourier Anal.Appl.,2005,11(5):497-509.

[7]Martell J M.Sharp maximal functions associated with approximations of the identity in spaces of homogeneous type and applications[J].Studia Mathematica,2002,161(2):1-28.

[8]Duong X T,McIntosh A.Singular integral operators with non-smooth kernel on irregular domains[J].Rev. Mat.Iberoamericana,1999,15(2):233-265.

[9]Rao M M,Ren Z D.Theory of Orlicz Spaces,Monographs and Textbooks in Pure and Applied Mathematics[M].New York:Marcel Dekker Inc.,1991.

Weighted estimates for a class of sigular integral operator

Zhu Weijie,Liu Suying,Zhao Kai,Jiang Xiutian
(College of Mathematics,Qingdao University,Qingdao266071,China)

In this paper,suppose that A is a Young function and M#Dis a new sharp maximal function.First, we introduce LA-H¨ormander condition.For the operator T satisfying LA-H¨ormander condition,we obtain the weighted estimates for the new sharp maximal function associated with operator T.Then,we use this result to prove that the Lp(ω)norm of the operator can be dominated by the Lp(ω)norm of a maximal function associated to the complementary function of A and a maximal function,for any weight ω in A∞and 0＜p＜∞.

sharp maximal function,Young function,Hardy-Littlewood maximal function, singular integral operator

O174.2

A

1008-5513(2013)03-0293-06

10.3969/j.issn.1008-5513.2013.03.011

2013-01-03.

國家自然科學基金(11041004);山東省自然科學基金(ZR2010AM032).

朱偉杰(1990-),碩士生,研究方向：調(diào)和分析.

趙凱(1960-),博士,教授,研究方向：調(diào)和分析和小波分析.

2010 MSC:42B20