ADDITIVE PERTURBATIONS OF LOCAL C-SEMIGROUPS?
Department of Mathematics,Fu Jen University,New Taipei City 24205,China
E-mail:cckuo@math.fju.edu.tw
ADDITIVE PERTURBATIONS OF LOCAL C-SEMIGROUPS?
Chung-Cheng KUO
Department of Mathematics,Fu Jen University,New Taipei City 24205,China
E-mail:cckuo@math.fju.edu.tw
In this paper,we apply the contraction mapping theorem to establish some bounded and unbounded additive perturbation theorems concerning local C-semigroups. Some growth conditions of perturbations of local C-semigroups are also established.
local C-semigroup;generator;abstract Cauchy problem;perturbation
2010 MR Subject Classifcation47D60;47D62
1 Introduction
Let X be a Banach space over F(=R or C)with norm‖·‖,and let L(X)denote the set of all bounded linear operators on X.For each 0<T0≤∞and each injection C∈L(X),a family S(·)(={S(t)|0≤t<T0})in L(X)is called a local C-semigroup on X if it is strongly continuous,S(0)=C on X and satisfes
(see[4,10-12,14,16-18]).In this case,the generator of S(·)is a linear operator A in X defned by
Moreover,we say that S(·)is locally Lipschitz continuous,if for each 0<t0<T0there exists a Kt0>0 such that
exponentially bounded,if T0=∞and there exist K,ω≥0 such that
exponentially Lipschitz continuous,if T0=∞and there exist K,ω≥0 such that
In general,the generator of a local C-semigroup may not be densely defned and a local C-semigroup may not be exponentially bounded,and is also called a C-semigroup if T0=∞(see[2,3,13]).Moreover,a local C-semigroup is not necessarily extendable to the half line [0,∞)(see[11])except for C=I,the case of C0-semigroup,that is,C=I and T0=∞(see [1,5,15]).Here I denotes the identity operator on X.Perturbation of local C-semigroups is one of the subjects in theory of semigroup which has been extensively studied by many authors appearing in[3,6-8,10-12,14,16-18].Some interesting applications of this topic are also illustrated there.In particular,Kuo[7]showed that A+B generates a local C-semigroup T(·) on X if A generates a local C-semigroup S(·)on X and one of following cases(i)-(iii)holds:

(ii)B is a bounded linear operator on X and S(·)B=BS(·);which is also established by Li and Shaw in[10]when S(·)is a C-semigroup on X.



2 Perturbation Theorems
In this section,we frst note some basic properties of a local C-semigroup and known results about connections between the generator of a local C-semigroup and strong solutions of the following abstract Cauchy problem:
where x∈X and f is an X-valued function defned on a subset of[0,T0).
Proposition 2.1(see[11])Let A be the generator of a local C-semigroup S(·)on X. Then
A is closed and
S(t)x∈D(A)and
Defnition 2.2Let A:D(A)?X→X be a closed linear operator in a Banach space X with domain D(A)and range R(A).A function u:[0,T0)→X is called a(strong)solution of ACP(A,f,x)if u∈C1((0,T0),X)∩C([0,T0),X)∩C((0,T0),[D(A)])and satisfes ACP(A,f,x). Here[D(A)]denotes the Banach space D(A)with norm|·|defned by|x|=‖x‖+‖Ax‖for all x∈D(A).
Remark 2.3u∈C([0,T0),[D(A)]),if f∈C([0,T0),X)and u is a(strong)solution of ACP(A,f,x)in C1([0,T0),X).
Theorem 2.4(see[11])A generates a local C-semigroup S(·)on X if and only if C-1AC=A and for each x∈X ACP(A,Cx,0)has a unique(strong)solution u(·,x)in C1([0,T0),X).In this case,we have
for all x∈X.Here jk(t)=tk/k!for t≥0 and k∈N∪{0}.

Lemma 2.6Let V(·)and Z(·)be strongly continuous families of bounded linear operators from X into a Banach space Y,and let W(·)be a strongly continuous family in L(Y)such that Z(·)x=V(·)x+W?Z(·)x on[0,T0)for all x∈X.Then Z(·)is exponentially bounded(resp., norm continuous,locally Lipschitz continuous,or exponentially Lipschitz continuous)if V(·) and W(·)both are.
ProofIt is easy to see from Gronwall’s inequality that Z(·)is exponentially bounded if V(·)and W(·)both are.Applying the decomposition
for 0≤t,h≤t+h<T0and x∈X,we get that Z(·)is also norm continuous(resp.,locally Lipschitz continuous or exponentially Lipschitz continuous)if V(·)and W(·)both are.?
The next result is a bounded perturbation theorem concerning local C-semigroups which is an extension of classical C0-semigroups as results in[1,5],and has been established by Shaw, Kuo and Li in[12]except for the growth conditions of T(·)when B is a bounded linear operator from X into R(C),and Xiao and Liang in[18]when B is a bounded linear operator from X into R(C)and S(·)is exponentially bounded.

for all x∈X.Moreover,T(·)is also exponentially bounded(resp.,norm continuous,locally Lipschitz continuous,or exponentially Lipschitz continuous)if S(·)is.
ProofWe frst show that C-1(A+B)C=A+B.Indeed,if x∈D(C-1(A+B)C)is given and C-1(A+B)Cx=y,then Cx∈D(A+B)=D(A)and Cy=(A+B)Cx=ACx+BCx, and so ACx=Cy-BCx∈R(C).Hence x∈D(C-1AC)=D(A)=D(A+B),which together with the assumption CB=BC on D(A)implies that D(C-1(A+B)C)=D(A+B) or equivalently,
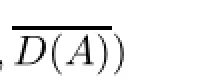
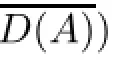
By induction,we have
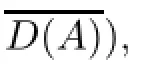

By slightly modifying the proof of Theorem 2.7,we can establish the next unbounded perturbation theorem concerning local C-semigroups on X.
Theorem 2.8Let S(·)be a local C-semigroup on X with generator A.Assume that B is a bounded linear operator from[D(A)]into R(C)such that CB=BC on D(A)and C-1Bx∈D(A)for all x∈D(A),and A+B is a closed linear operator from D(A)into X. Then A+B generates a local C-semigroup T(·)on X satisfying
ProofJust as in the proof of Theorem 2.7,we have C-1(A+B)C=A+B.Now if 0<t0<T0and f∈C([0,t0],[D(A)])are given.By(2.3)-(2.4)and the fact of C-1Bx∈D(A) for all x∈D(A),we have S?C-1Bf(·)∈C1([0,t0],X),AS?C-1Bf(·)=S?AC-1Bf(·)and
Here D1denotes the derivative of a function.Since
for all 0≤t≤t0,we have
for all 0≤t≤t0.Here
For each x∈X and 0<t0<T0we defne U:C([0,t0],[D(A)])→C([0,t0],[D(A)])by U(f)(·)=j0?S(·)x+S?C-1Bf(·)on[0,t0]for all f∈C([0,t0],[D(A)]).By induction,we also have

By slightly modifying the proof of Theorem 2.8,the next new unbounded perturbation theorem concerning locally Lipschitz continuous local C-semigroups on X is also attained.

for all x∈X.
ProofBy the closedness of A,the local Lipschitz continuity of S(·)and the fact of{x∈X|S(·)x∈C1([0,T0),X)}is a closed subspace of X containing D(A),we have S?C-1Bf(·)∈C1([0,T0),X)and

for all 0<t0<T0.Similarly,we can obtain from(2.14)and(2.17)that A+B generates a local C-semigroup T(·)on X satisfying(2.16).
The conclusion of Theorem 2.8 is still true when the assumption that A+B is a closed linear operator from D(A)into X is replaced by assuming that ρC(A)={λ∈F|λ-A is injective,R(C)?R(λ-A),and(λ-A)-1C∈L(X)}is nonempty and AB=BA on D(A2).
Theorem 2.10Let S(·)be a local C-semigroup on X with generator A.Assume that B is a bounded linear operator from[D(A)]into R(C)such that CB=BC on D(A),C-1Bx∈D(A) for all x∈D(A),ρC(A)is nonempty and AB=BA on D(A2).Then A+B generates a local C-semigroup T(·)on X satisfying(2.9).
ProofClearly,it sufces to show that A+B is a closed linear operator from D(A)into X or equivalently,λ-(A+B)is.Here λ∈ρC(A)is fxed.Indeed,if xm∈D(A),xm→x in X and ym=[λ-(A+B)]xm→y in X.Since
on D(A),we have
and so(λ-A)-1Cy+B(λ-A)-1Cx=Cx∈R(C).Hence
Since R(B)?D(A),we also have
and so(λ-A)-1Cx∈D(A2)and
Hence[λ-(A+B)]Cx=Cy∈R(C).This implies that x∈D(C-1[λ-(A+B)]C)= D(λ-(A+B))=D(A)and[λ-(A+B)]x=C-1(λ-(A+B))Cx=y.Consequently, λ-(A+B)is closed.?
Corollary 2.11Let S(·)be a local C-semigroup on X with generator A.Assume that B is a bounded linear operator from[D(A)]into R(C2)such that CB=BC on D(A),C-2Bx∈D(A)for all x∈D(A),ρC(A)is nonempty and AB=BA on D(A2).Then A+B generates a local C-semigroup T(·)on X satisfying
for all x∈X.Here λ∈ρC(A).Moreover,T(·)is also exponentially bounded(resp.,norm continuous,locally Lipschitz continuous,or exponentially Lipschitz continuous)if S(·)is.
ProofIt is easy to see from the assumption AB=BA on D(A2)that we have AC-1Bx= C-1BAx for all x∈D(A2).Just as in the proof of Theorem 2.8,we can show that for each x∈X there exists a unique function wxin C([0,T0),X)such that
and so j0?wxis the unique solution of
in C1([0,T0),X).Hence u=j0?wxis the unique function in C1([0,T0),X)such that u′= Au+Cx+Bu=(A+B)u+Cx on[0,T0)and u(0)=0,which together with Theorem 2.4 implies that A+B generates a local C-semigroup T(·)on X satisfying(2.18)and T(·)x=wx(·) for all x∈X.Applying Lemma 2.6 again,we get that T(·)is also exponentially bounded(resp., norm continuous,locally Lipschitz continuous,or exponentially Lipschitz continuous)if S(·)is. ?
By Theorem 2.9,the next unbounded perturbation result concerning locally Lipschitz continuous local C-semigroups on X is also attained.
Corollary 2.12Let S(·)be a locally Lipschitz continuous local C-semigroup on X with generator A.Assume that B is a bounded linear operator from[D(A)]into R(C2)such that CB=BC on D(A),ρC(A)is nonempty and AB=BA on D(A2),and A+B is a closed linear operator from D(A)into X.Then A+B generates a local C-semigroup T(·)on X satisfying
for all x∈X.Here λ∈ρC(A).
ProofBy Theorem 2.9,A+B generates a local C-semigroup T(·)on X satisfying(2.16). To show that(2.19)holds for all x∈X,we shall frst show that
for all x∈X.Indeed,if x∈X is given.By the assumption of AB=BA on D(A2),we have AC-2B=C-2BA on D(A2).Since
we have

we have
Combining the closedness of λ-A and the boundedness of C-2B(λ-A)-1with the strong continuity of T(·),we have
which implies that D1S?C-1B~T(·)x=(λ-A)S?C-2B(λ-A)-1CT(·)x.Consequently,(2.19) holds for all x∈X.?
By slightly modifying the proofs of Corollaries 2.11 and 2.12,the next two unbounded perturbation results are also attained when the assumptions that B is a bounded linear operator from[D(A)]into R(C2)and ρC(A)is nonempty are replaced by assuming that B is a bounded linear operator from[D(A)]into R(C)and ρ(A)(,resolvent set of A,)is nonempty.
Corollary 2.13Let S(·)be a local C-semigroup on X with generator A.Assume that B is a bounded linear operator from[D(A)]into R(C)such that CB=BC on D(A),C-1Bx∈D(A) for all x∈D(A),ρ(A)is nonempty and AB=BA on D(A2).Then A+B generates a local C-semigroup T(·)on X satisfying
for all x∈X.Here λ∈ρ(A).Moreover,T(·)is also exponentially bounded(resp.,norm continuous,locally Lipschitz continuous,or exponentially Lipschitz continuous)if S(·)is.

for all x∈X.Here λ∈ρ(A).
The conclusions of Theorem 2.10 and Corollary 2.11 are still true when the assumptions that ρC(A)is nonempty and AB=BA on D(A2)are replaced by assuming that ρC(A+B)is nonempty.
Theorem 2.15Let S(·)be a local C-semigroup on X with generator A.Assume that B is a bounded linear operator from[D(A)]into R(C)such that CB=BC on D(A),C-1Bx∈D(A) for all x∈D(A),and ρC(A+B)is nonempty.Then A+B generates a local C-semigroup T(·) on X satisfying(2.9).
ProofClearly,it sufces to show that λ-(A+B)is a closed linear operator from D(A) into X.Here λ∈ρC(A+B)is fxed.Indeed,if xm∈D(A+B)(=D(A)),xm→x in X and ym=[λ-(A+B)]xm→y in X,then(λ-(A+B))-1C(λ-(A+B))xm=Cxm→Cx and(λ-(A+B))-1C(λ-(A+B))xm→(λ-(A+B))-1Cy,so that(λ-(A+B))-1Cy=Cx∈D(λ-(A+B))(=D(A))and(λ-(A+B))Cx=Cy.Hence ACx=Cy-BCx+λCx∈R(C), which implies that x∈D(C-1AC)=D(A)=D(λ-(A+B))and y=(λ-(A+B))x. Consequently,λ-(A+B)is closed.?

Corollary 2.17Let S(·)be a local C-semigroup on X with generator A.Assume that B is a bounded linear operator from[D(A)]into R(C2)such that CB=BC on D(A),C-2Bx∈D(A)for all x∈D(A),and ρC(A+B)is nonempty.Then A+B generates a local C-semigroup T(·)on X satisfying(2.9).Moreover,
for all x∈X if AB=BA on D(A2).Here λ∈ρC(A+B).In this case,T(·)is also exponentially bounded(resp.,norm continuous,locally Lipschitz continuous,or exponentially Lipschitz continuous)if S(·)is.
By Theorem 2.16,the next unbounded perturbation result concerning locally Lipschitz continuous local C-semigroups on X is also attained.
Corollary 2.18Let S(·)be a locally Lipschitz continuous local C-semigroup on X with generator A.Assume that B is a bounded linear operator from[D(A)]into R(C2)such that CB=BC on D(A)and ρC(A+B)is nonempty.Then A+B generates a local C-semigroup T(·)on X satisfying(2.16).Moreover,
for all x∈X if AB=BA on D(A2).Here λ∈ρC(A+B).
Similarly,the next two unbounded perturbation results are also attained when the assumptions that B is a bounded linear operator from[D(A)]into R(C2)and ρC(A+B)is nonempty are replaced by assuming that B is a bounded linear operator from[D(A)]into R(C)and ρ(A+B)is nonempty.
Corollary 2.19Let S(·)be a local C-semigroup on X with generator A.Assume that B is a bounded linear operator from[D(A)]into R(C)such that CB=BC on D(A),C-1Bx∈D(A) for all x∈D(A),and ρ(A+B)is nonempty.Then A+B generates a local C-semigroup T(·) on X satisfying(2.9).Moreover,
for all x∈X if AB=BA on D(A2).Here λ∈ρ(A+B).In this case,T(·)is also exponentially bounded(resp.,norm continuous,locally Lipschitz continuous,or exponentially Lipschitz continuous)if S(·)is.

for all x∈X if AB=BA on D(A2).Here λ∈ρ(A+B).


[1]Arendt W,Batty C J K,Hieber H,Neubrander F.Vecctor-Valued Laplace Transforms and Cauchy Problems 96.Basel,Boston,Berlin:Birkhauser Verlag,2001
[2]Davies E S,Pang M M.The cauchy problem and a generalization of the Hille-Yosida theorem.Proc London Math Soc,1987,55:181-208
[3]DeLaubenfuls R.C-Semigroups and the abstract cauchy problem.J Funct Anal,1993,111:44-61
[4]Gao M.Local C-semigroups and local C-cosine functions.Acta Math Sci,1999,19:201-213
[5]Goldstein J A.Semigroups of Linear Operators and Applications.Oxford,1985
[6]Liang J,Xiao T J,Li F.Multiplicative perturbations of local C-regularized semigroups.Semigroup Forum, 2006,72(3):375-386
[7]Kuo C C.On perturbation of α-times integrated C-semigroups.Taiwanese J Math,2010,14(5):1979-1992
[8]Kuo C C.Multiplicative perturbations of local C-semigroups.Proc Math Sci,2015,125(1):45-55
[9]Kuo C C.On existence and approximation of solutions of abstract cauchy problem.Taiwanese J Math, 2009,13:137-155
[10]Li Y C,Shaw S Y.On characterization and perturbation of local C-semigroups.Proc Amer Math Soc, 2007,135:1097-1106
[11]Shaw S Y,Kuo C C.Generation of local C-semigroups and solvability of the abstract cauchy problems. Taiwanese J Math,2005,9:291-311
[12]Shaw S Y,Kuo C C,Li Y C.Perturbation of local C-semigroups.Nonlinear Analysis,2005,63:2569-2574
[13]Tanaka N,Miyadera I.C-semigroups and the abstract cauchy problem.J Math Anal Appl,1992,170: 196-206
[14]Tanaka N,Okazawa N.Local C-semigroups and local integrated semigroups.Proc London Math Soc,1990, 61:63-90
[15]Xiao T J,Liang J.Laplace transforms and integrated,regularized semigroups in locally convex spaces.J Funct Anal,1997,148(2):448-479
[16]Xiao T J,Liang J.Multiplicative perturbations of C-regularized semigroups.Comput Math Appl,2001, 41:1215-1221
[17]Xiao T J,Liang J,Li F.A perturbation theorem of miyadera type for local C-regularized semigroups. Taiwanese J Math,2006,10:153-162
[18]Xiao T J,Liang J.The cauchy problem for higher-order abstract diferential equations//Lectures Notes in Math,1701.Springer,1998
?Received March 18,2014;revised April 29,2015.Research partially supported by the National Science Council of Taiwan.
 Acta Mathematica Scientia(English Series)2015年6期
Acta Mathematica Scientia(English Series)2015年6期
- Acta Mathematica Scientia(English Series)的其它文章
- THEORY AND APPLICATION OF FRACTIONAL STEP CHARACTERISTIC FINITE DIFFERENCE METHOD IN NUMERICAL SIMULATION OF SECOND ORDER ENHANCED OIL PRODUCTION?
- BLOWING UP AND MULTIPLICITY OF SOLUTIONS FOR A FOURTH-ORDER EQUATION WITH CRITICAL NONLINEARITY?
- QUADRATIC ρ-FUNCTIONAL INEQUALITIES IN BANACH SPACES?
- STABILITY OF SOME POSITIVE LINEAR OPERATORS ON COMPACT DISK?
- A NOTE ON THE REPRESENTATIONS FOR THE GENERALIZED DRAZIN INVERSE OF BLOCK MATRICES?
- ON THE BOUNDEDNESS AND THE NORM OF A CLASS OF INTEGRAL OPERATORS?
