張 超,趙承業(yè)

(中國(guó)計(jì)量學(xué)院 理學(xué)院,浙江 杭州 310018)

計(jì)算樹(shù)的[1,2]-數(shù)的算法研究

張 超,趙承業(yè)

(中國(guó)計(jì)量學(xué)院 理學(xué)院,浙江 杭州 310018)

圖G的一個(gè)點(diǎn)集S是[1,2]-集,若每個(gè)不在S中的點(diǎn)至少與S中的1個(gè)點(diǎn)相鄰且至多與S中的2個(gè)點(diǎn)相鄰.一個(gè)圖的所有[1,2]-集中元素個(gè)數(shù)最小的集合,其元素個(gè)數(shù)稱(chēng)為圖的[1,2]-數(shù).針對(duì)樹(shù)的[1,2]-數(shù)的計(jì)算問(wèn)題進(jìn)行研究.首先,根據(jù)[1,2]-數(shù)的定義給出了一個(gè)0-1規(guī)劃模型,求解這個(gè)0-1規(guī)劃可以得到圖的[1,2]-數(shù)的精確值.然后,基于貪婪策略將樹(shù)進(jìn)行星分解,給出計(jì)算[1,2]-數(shù)的兩個(gè)近似算法.最后,分析了兩個(gè)近似算法的計(jì)算復(fù)雜度和性能.

[1,2]-數(shù);0-1規(guī)劃;貪婪策略;近似算法

一個(gè)集合S?V(G)被稱(chēng)為圖G的支配集(Dominating Set)[1],如果其滿(mǎn)足下面的條件:對(duì)圖G的任意的頂點(diǎn)v,或者屬于S或者與S中的頂點(diǎn)相鄰接.我們把頂點(diǎn)數(shù)目最少的支配集稱(chēng)為圖的最小支配集(Minimum Dominating Set),它的頂點(diǎn)數(shù)目稱(chēng)為圖的支配數(shù)(Dominating Number),記作γ(G).對(duì)于支配集S,若有任意的點(diǎn)v∈V(G)S滿(mǎn)足1≤|N(v)∩S|≤2,則此支配集S為圖G的[1,2]-集[2],其最小階數(shù)即為圖的[1,2]-數(shù)([1,2]-number),記作γ[1,2](G).

支配集在許多計(jì)算機(jī)領(lǐng)域有廣泛的應(yīng)用,例如連通支配集在無(wú)線(xiàn)網(wǎng)絡(luò)的虛擬骨干構(gòu)造中具有很重要的應(yīng)用價(jià)值.[1,2]-集的概念是CHELLALI[2]等人2013年提出的一類(lèi)受限的支配集的概念.他們給出了一般的[j,k]-集的概念,即滿(mǎn)足j≤|N(v)∩S|≤k的集合,并重點(diǎn)討論了j=1,k=2,3情形下的一些問(wèn)題.他們證明了一般二分圖的[1,2]-集問(wèn)題是一個(gè)NPC問(wèn)題,因此計(jì)算圖的[1,2]-數(shù)問(wèn)題是一個(gè)比較復(fù)雜的問(wèn)題.

本文針對(duì)最簡(jiǎn)單的連通圖——樹(shù),考慮樹(shù)的的[1,2]-數(shù)的計(jì)算問(wèn)題.我們首先考慮計(jì)算樹(shù)的[1,2]-數(shù)精確算法,由[1,2]-數(shù)定義我們建立0-1規(guī)劃模型,通過(guò)求解0-1規(guī)劃模型得到樹(shù)的[1,2]-數(shù)的精確值.考慮到0-1規(guī)劃的局限性(能計(jì)算的頂點(diǎn)數(shù)有限),我們基于貪婪策略給出了兩個(gè)近似算法,分析了其計(jì)算復(fù)雜性并通過(guò)實(shí)驗(yàn)分析了這兩個(gè)算法的性能.

1 計(jì)算[1,2]-數(shù)的0-1規(guī)劃模型

對(duì)任意一個(gè)圖G有鄰接矩陣A,I為單位矩陣,令向量X=(x1,x2,…,xn),其中xj表示圖G中的頂點(diǎn),若在[1,2]-集中則賦值為1;反之,不在[1,2]-集中賦值為0,則圖G的[1,2]-數(shù)即為式(1)0-1規(guī)劃模型的解.

(1)

式(1)中：xj=0,1,i=1,2,…,n.

圖1是一棵20個(gè)頂點(diǎn)的樹(shù),利用上面的0-1規(guī)劃模型求解此樹(shù)的[1,2]-數(shù),如圖所示,其中黑色的節(jié)點(diǎn)構(gòu)成了這個(gè)圖的[1,2]-集,其精確值為7.

因?yàn)橐话?-1規(guī)劃的求解,其復(fù)雜性是指數(shù)階的,因此利用上面的0-1規(guī)劃模型求解樹(shù)的[1,2]-數(shù)有很大的局限性.我們使用處理器為ADM Athlon(tm)Ⅱ X3 425@2.7 GHz的計(jì)算機(jī),利用Matlab R2009a中的優(yōu)化工具箱中相關(guān)函數(shù)編寫(xiě)了求解上面0-1規(guī)劃模型的程序.通過(guò)大量的數(shù)據(jù)實(shí)驗(yàn)表明,此模型適用范圍在400個(gè)頂點(diǎn)以下.

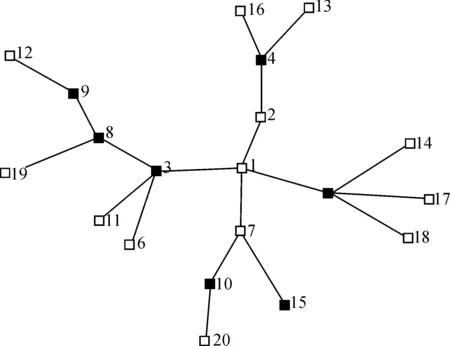
圖1 0-1規(guī)劃模型計(jì)算20個(gè)頂點(diǎn)的樹(shù)的[1,2]-數(shù)Figure 1 0-1 programming model calculating [1,2]-number of tree with 20 vertices

2 基于貪婪策略的計(jì)算樹(shù)的[1,2]-數(shù)的近似算法

借鑒文獻(xiàn)[3]中構(gòu)造連通支配集的近似算法的思想,先利用貪婪策略構(gòu)造一個(gè)圖的支配集,然后再添加一些點(diǎn)到這個(gè)支配集中直到滿(mǎn)足[1,2]-集的條件.基于不同貪婪策略,得到的近似算法也不同.我們下面給出兩個(gè)近似算法:基于頂點(diǎn)的最大度對(duì)樹(shù)進(jìn)行星分解;基于具有最多葉子的節(jié)點(diǎn)對(duì)樹(shù)進(jìn)行星分解.

2.1 基于頂點(diǎn)的最大度MD(Maximum Degree)

對(duì)任意一棵樹(shù)以當(dāng)前最大度頂點(diǎn)為中心進(jìn)行星分解.首先,刪除選擇的最大度點(diǎn)及其相鄰點(diǎn)和邊,樹(shù)的余下部分依次循環(huán)此操作直至剩下的點(diǎn)為孤立點(diǎn)或孤立點(diǎn)集,那么每次找到的最大度點(diǎn)和最后剩下的孤立點(diǎn)就構(gòu)成一個(gè)集合C,并且C之外的點(diǎn)若與C內(nèi)的點(diǎn)相鄰個(gè)數(shù)超過(guò)2時(shí)要把該點(diǎn)加入集合C,從而最終得到的集合C就是這個(gè)樹(shù)的[1,2]-集,其中集合C的節(jié)點(diǎn)元素個(gè)數(shù)即為該算法計(jì)算得到的樹(shù)的[1,2]-數(shù).

算法2.1 基于最大度點(diǎn)的近似算法(MD Algorithm)

輸入:任意一棵樹(shù)T.

輸出:T的[1,2]-集C的階數(shù).

算法描述:

C=φ,W=V;

選取樹(shù)T最大度節(jié)點(diǎn)c,C=C∪{c},W=W-N[c];

WhileW不是孤立點(diǎn)集

do 選取T[W]的最大度節(jié)點(diǎn)c,C=C∪{c},W=W-N[c];

計(jì)算集合C的節(jié)點(diǎn)個(gè)數(shù).

定理2.1 算法2.1的時(shí)間復(fù)雜度是O(n2)的,其中n是樹(shù)的頂點(diǎn)數(shù).

證明:算法2.1的時(shí)間復(fù)雜度主要依賴(lài)兩個(gè)while循環(huán)的時(shí)間復(fù)雜度.

第一個(gè)while循環(huán),判斷W是否為孤立點(diǎn)集的時(shí)間復(fù)雜度是O(n)的;尋找T[W]的最大度節(jié)點(diǎn)的復(fù)雜度也是O(n)的;因此第一個(gè)while循環(huán)的復(fù)雜度是O(n2)的.

第二個(gè)while循環(huán),判斷是否存在滿(mǎn)足要求的u的時(shí)間復(fù)雜度是O(n)的;C和它的補(bǔ)集的增減操作的時(shí)間復(fù)雜度都是O(n)的;因此第二個(gè)while循環(huán)的復(fù)雜度是O(n2)的.

其他操作的時(shí)間復(fù)雜度不超過(guò)O(n)的,因此算法2.1的時(shí)間復(fù)雜度是O(n2)的.

圖2給出對(duì)圖1中的同一棵樹(shù),MD算法的計(jì)算結(jié)果.MD算法計(jì)算速度比0-1規(guī)劃模型有顯著地提高,但相應(yīng)地計(jì)算精度下降了.根據(jù)樹(shù)結(jié)構(gòu)的特點(diǎn),我們進(jìn)行了改進(jìn),給出了基于最多葉子節(jié)點(diǎn)的近似算法.

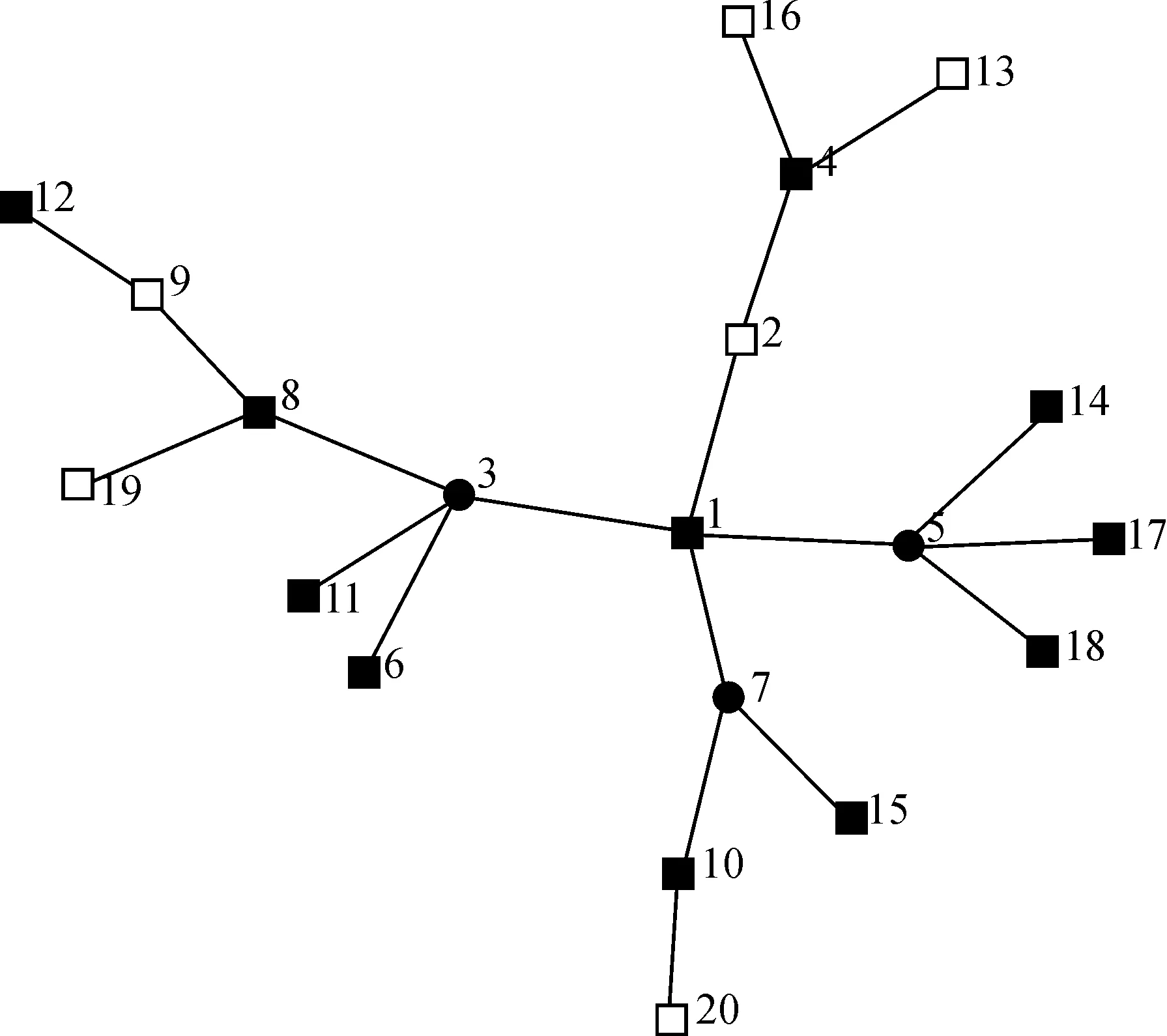
圖2 基于最大度點(diǎn)的近似算法計(jì)算20個(gè)頂點(diǎn)的樹(shù)的[1,2]-數(shù)Figure 2 Calculating [1, 2]-number of tree with 20 vertices by MD Algorithm

2.2 基于最多葉子的節(jié)點(diǎn)ML(Maximum Leaves)

考慮到MD算法可以在刪除節(jié)點(diǎn)時(shí),令許多葉子節(jié)點(diǎn)變成孤立點(diǎn),造成許多不必要的頂點(diǎn)也進(jìn)入到集合C中,我們?cè)谶x擇星結(jié)構(gòu)的中心點(diǎn)時(shí),把最大度改成有最多葉子的節(jié)點(diǎn),就可以避免這種情況,基于這個(gè)思想,我們給出下面的算法:

算法2.2 基于最多葉子節(jié)點(diǎn)的近似算法(ML Algorithm)

輸入:任意一棵樹(shù)T.

輸出:T的[1,2]-集C的階數(shù).

算法描述:

C=φ,W=V;

選取樹(shù)T中葉子最多的節(jié)點(diǎn)c,C=C∪{c},W=W-N[c];

WhileW不是孤立點(diǎn)集

do 選取T[W]中葉子最多的節(jié)點(diǎn)c,C=C∪{c},W=W-N[c];

計(jì)算集合C的節(jié)點(diǎn)個(gè)數(shù).

定理2.2 算法2.2的時(shí)間復(fù)雜度是O(n3)的,其中n是樹(shù)的頂點(diǎn)數(shù).

證明:算法2.2的時(shí)間復(fù)雜度主要依賴(lài)兩個(gè)while循環(huán)的時(shí)間復(fù)雜度.

第一個(gè)while循環(huán),判斷W是否為孤立點(diǎn)集的時(shí)間復(fù)雜度是O(n)的;尋找T[W]的有最多葉子的節(jié)點(diǎn)復(fù)雜度是O(n2)的;因此第一個(gè)while循環(huán)的復(fù)雜度是O(n3)的.

第二個(gè)while循環(huán),判斷是否存在滿(mǎn)足要求的u的時(shí)間復(fù)雜度是O(n)的;C和它的補(bǔ)集的增減操作的時(shí)間復(fù)雜度都是O(n)的;因此第二個(gè)while循環(huán)的復(fù)雜度是O(n2)的.

其他操作的時(shí)間復(fù)雜度不超過(guò)O(n2)的,因此算法2.2的時(shí)間復(fù)雜度是O(n3)的.

圖3給出對(duì)圖1中的同一棵樹(shù)ML算法的計(jì)算結(jié)果.

圖3 基于最多葉子的近似算法計(jì)算20個(gè)頂點(diǎn)的樹(shù)的[1,2]-數(shù)Figure 3 Calculating [1, 2]-number of tree with 20 vertices by ML Algorithm

3 實(shí)驗(yàn)結(jié)果與對(duì)比分析

綜合上述的兩類(lèi)算法,分別為0-1規(guī)劃模型(IP)的精確算法和兩種基于貪婪策略的近似算法,其中近似算法包括基于尋找最大度點(diǎn)圖分解的算法(MD)和基于尋找最多葉子節(jié)點(diǎn)圖分解的算法(ML).本文中所有的實(shí)驗(yàn)均是使用ADM Athlon(tm)Ⅱ X3 425@2.7 GHz處理器在Matlab R2009a環(huán)境下運(yùn)行.下面針對(duì)這三種算法,在算法的時(shí)間復(fù)雜度和結(jié)果的精確性?xún)煞矫嫔线M(jìn)行對(duì)比分析.

3.1 時(shí)間復(fù)雜度對(duì)比分析

表1 計(jì)算不同節(jié)點(diǎn)個(gè)數(shù)的樹(shù)的[1,2]-數(shù)的平均運(yùn)行時(shí)間(s)

Table 1 Average running time calculating [1,2]-number of trees with different vertices (s)

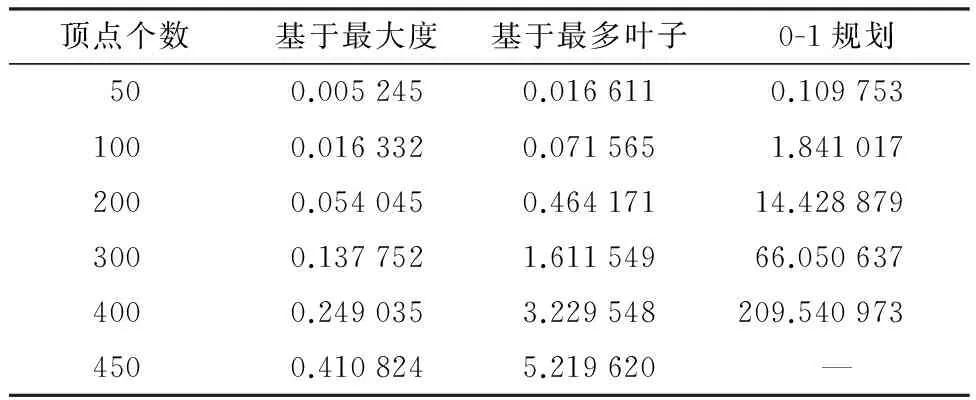
頂點(diǎn)個(gè)數(shù)基于最大度基于最多葉子0-1規(guī)劃500.0052450.0166110.1097531000.0163320.0715651.8410172000.0540450.46417114.4288793000.1377521.61154966.0506374000.2490353.229548209.5409734500.4108245.219620—

3.2 精確性對(duì)比分析

表2 不同節(jié)點(diǎn)個(gè)數(shù)的平均計(jì)算結(jié)果

Table 2 Average calculation results with different vertices

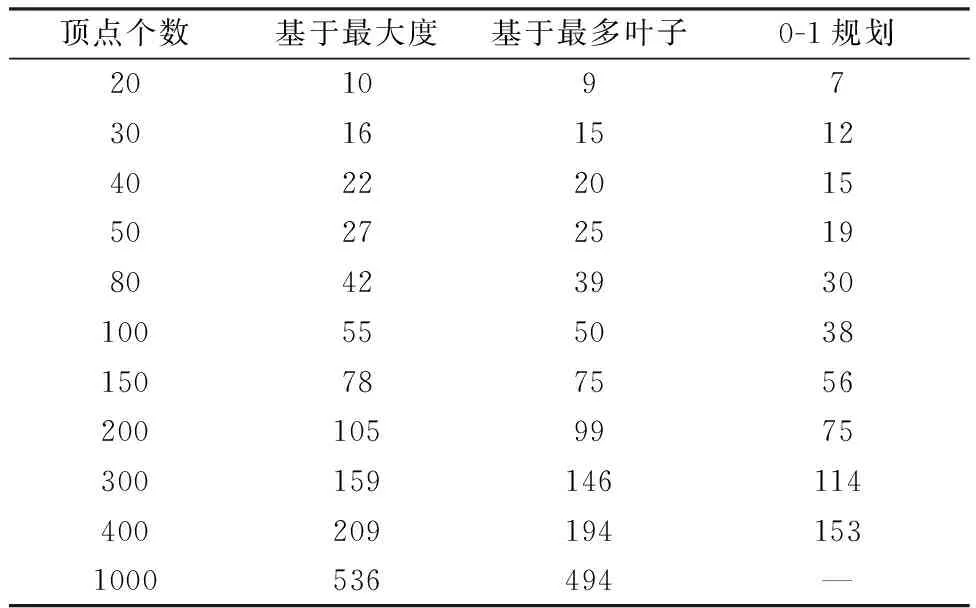
頂點(diǎn)個(gè)數(shù)基于最大度基于最多葉子0-1規(guī)劃2010973016151240222015502725198042393010055503815078755620010599753001591461144002091941531000536494—

4 結(jié) 語(yǔ)

本文給出了計(jì)算樹(shù)的[1,2]-數(shù)的精確算法和兩個(gè)近似算法,分析了近似算法的計(jì)算復(fù)雜性并通過(guò)實(shí)驗(yàn)比較了算法的時(shí)間性能和結(jié)果的精確性.文獻(xiàn)[4]中給出了許多圖的不同類(lèi)型的支配數(shù)的算法,其中對(duì)于樹(shù),很多類(lèi)型的支配數(shù)都有相應(yīng)的線(xiàn)性算法.因此,對(duì)于是否存在計(jì)算樹(shù)的[1,2]-數(shù)的線(xiàn)性算法是一個(gè)值得深入研究的問(wèn)題.通過(guò)我們的分析,這個(gè)問(wèn)題比文獻(xiàn)[4]中的問(wèn)題復(fù)雜得多,因此設(shè)計(jì)比較好的近似算法也是需要重點(diǎn)研究的問(wèn)題之一.

[1] BONDY J A, MURTY U S R. Graph theory with applications[M].New York: Macmillan,1976：53-269.

[2] CHELLALI M, HAYNES T W, HEDETNIEMI S T. [1,2]-sets in graphs[J].Discrete Applied Mathematics,2013,161(18):2885-2893.

[3] GUHA S, KHULLER S. Approximation algorithms for connected dominating sets[J].Algorithmica,1998,20(4):374-387.

[4] HAYNES T W, HEDETNIEMI S T, SLATER P J. Fundamentals of Domination in Graphs[M].New York: Marcel Dekker,1998,32-95.

Research on the algorithms of computing the [1,2]-number of trees

ZHANG Chao, ZHAO Chengye

(College of Sciences, China Jiliang University, Hangzhou 310018, China)

A vertex setSof a graphGis a [1,2]-set. Every vertex which is not inSsatisfies that it is adjacent to at least one vertex, but not more than two vertices inS. The [1,2]-number equals the minimum cardinality of a [1,2]-set in G. The algorithms of calculating the [1,2]-number of trees were studied. Firstly, a 0-1 programming model was constructed according to the definition of the [1,2]-number. The exact [1,2]-number of the tree was got by solving the 0-1 programming model. Through star-decomposition of the tree based on the greedy strategy, two approximate algorithms, which calculated the [1,2]-number of trees, were got. Finally, the computing complexity and the performances of the two approximate algorithms were analyzed.

[1,2]-number; 0-1 programming; greedy strategy; approximate algorithm

1004-1540(2015)02-0243-04

10.3969/j.issn.1004-1540.2015.02.022

2015-03-01 《中國(guó)計(jì)量學(xué)院學(xué)報(bào)》網(wǎng)址：zgjl.cbpt.cnki.net

國(guó)家自然科學(xué)基金面上項(xiàng)目(No.61173002).

O157.5

A