Second Order Estimates for Non-concave Hessian Type Elliptic Equations on Riemannian Manifolds

Heming Jiao

Department of Mathematics,Harbin Institute of Technology,Harbin 150001,Helongjiang Province,P.R.China

Second Order Estimates for Non-concave Hessian Type Elliptic Equations on Riemannian Manifolds

Heming Jiao?

Department of Mathematics,Harbin Institute of Technology,Harbin 150001,Helongjiang Province,P.R.China

.In this paper,we derive second order estimates for a class of non-concave Hessian type elliptic equations on Riemannian manifolds.By applying a new method forC2estimates,we can weaken some conditions,which works for some non-concave equations.Gradient estimates are also obtained.

AMS subject classifications:35J15,58J05,35B45.

Non-concave fully nonlinear elliptic equations,Riemannian manifolds,a priori estimates,Dirichlet problem,subsolutions.

1 Introduction

In this paper we continue our previous work in[5,6]to study the Dirichlet problem for Hessian type equations

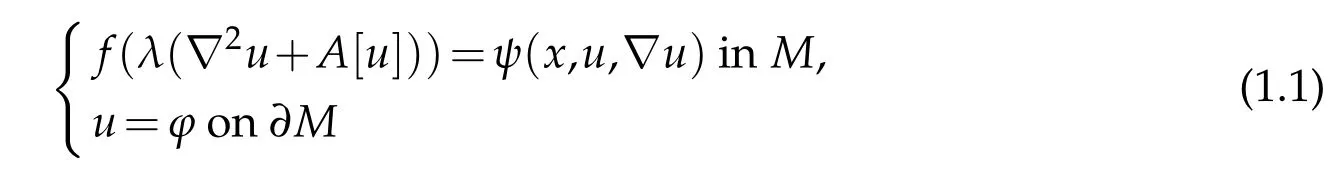
on a compact Riemannian manifold(Mn,g)of dimensionn≥2 with smooth boundary?M,wherefis a symmetric smooth function ofnvariables,?u=duwhich is often identified with the gradient ofu,?2udenotes the Hessian ofu,A[u]=A(x,u,?u)is a(0,2)tensor which may depend onuand?u,and

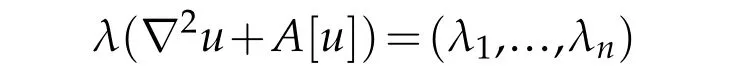
denotes the eigenvalues of?2u+A[u]with respect to the metricg.

Our motivation to study equations(1.1)is mainly from their significant applications in differential geometry(see[5]).

As in[1],the functionf∈C2(Γ)is assumed to be defined in an open,convex,symmetric cone Γ?Rnwith vertex at the origin,

and to satisfy

which implies(1.1)is elliptic for the solutionu∈C2(ˉM)satisfyingλ(?2u+A[u])∈Γ;we shall call such functionsadmissible(see[1]).

Another fundamental assumption is

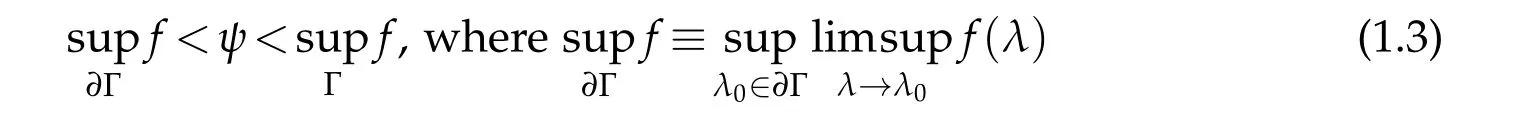
which prevents the degeneracy of(1.1).

We assume in this paper thatA[u]andψ[u]are smooth onˉMforu∈C∞(ˉM)and?∈C∞(?M).As in[5]and[6],we shall use the notations

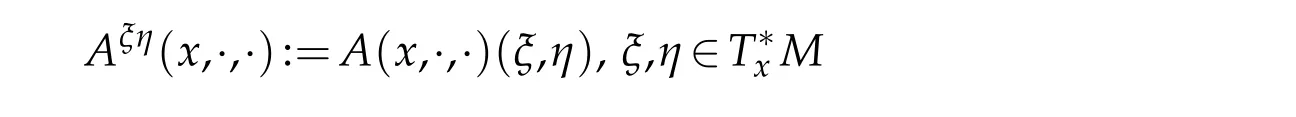
and therefore,Aξη[v]:=Aξη(x,v,?v)for a functionv∈C2(M).

We assume that

and moreover,there exists an admissible subsolutionu∈C2(ˉM)satisfying

Now we can state our main theorem as follows.

For instance,we can choose

in this example.

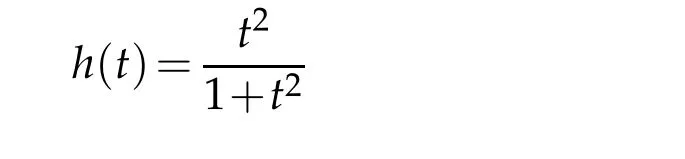
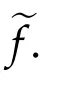
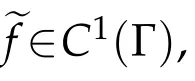
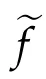
Theorem 1.2.Assume that(1.2),(1.3),(1.5)-(1.7)and(1.9)-(1.10)hold.Let u∈C4(ˉM)be an admissible solution of the Dirichlet problem(1.1)with u≥u onˉM.Then(1.8)is valid.

Remark 1.1.Guan[4]studied the equation

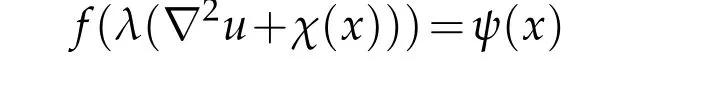
and established the second order estimates under conditions

for someR0＞0 and

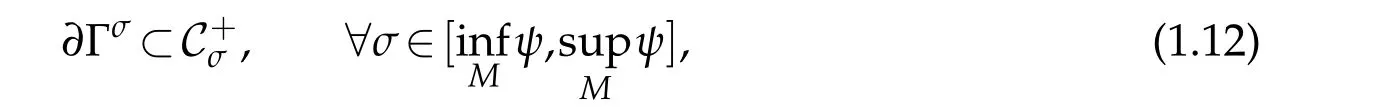
where Γσ={λ∈Γ:f(λ)＞σ}and C+σis the tangent cone at infinity to Γσ(see[4]for the definition).In[4]the author also propose the question whetherone can obtain the second order estimates with

in place of(1.12).

Clearly the condition(1.9)implies(1.11)and(1.13).Another interesting question would be whether(1.9)is equivalent to(1.11)and(1.13).

In this paper,we first prove some useful properties of the concave envelope in Section 2.Theorem 1.1 and Theorem 1.2 are proved in Section 3 which is devoted to the global second order estimates and Section 4 where the boundary estimates are established.In Section 5 we prove some theorems about gradient estimates.

2 Properties of the concave envelope

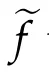
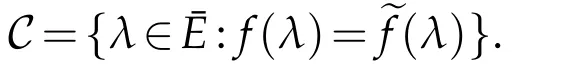
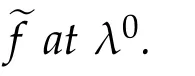
Then there exists at most n+1points λi∈ Csuch that

for

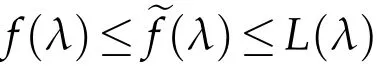
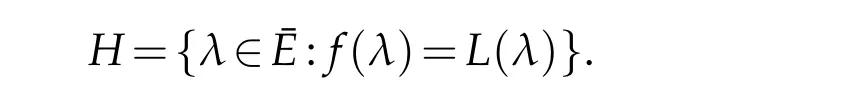
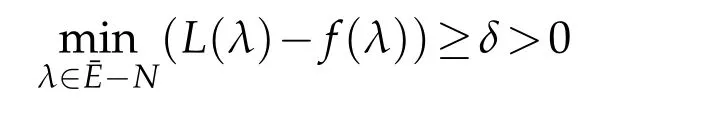
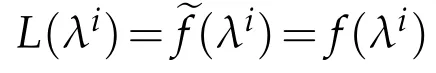
Lemma 2.2.ef∈C1,1(Γ)and(1.4)holds.

Proof.For anyλ0∈Γ we first show that efis derivable atλ0.We may assumeλ0∈E?C and we can find a compact setK?Econtainingλ0.Chooseλias in Lemma 2.1 such that(2.1)holds.

We claim that there exists a compact setK0?ˉEand an indexjsatisfying dist(K0,?Γ)≥c0＞0,λj∈K0andtj≥c1＞0 for some constantsc0andc1.

In fact,letδ0=minKf＞0.There exists a compact setK0?ˉEsuch thatf＜δ0/(n+1)inˉE?K0and dist(K0,?Γ)≥c0＞0 for some constantc0depending onδ0,nandfsincef≤0 on?Γ.We see that

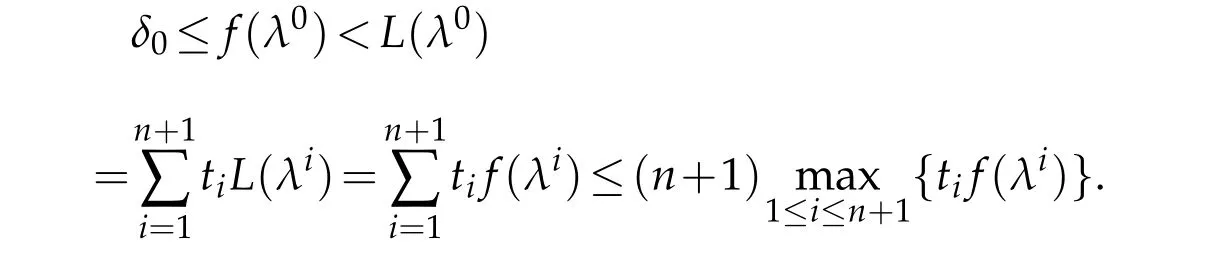
Lettjf(λj)=max1≤i≤n+1{tif(λi)}.Therefore,we have

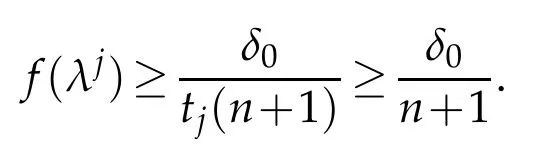
It follows thatλj∈K0by the definition ofK0.On the other hand,

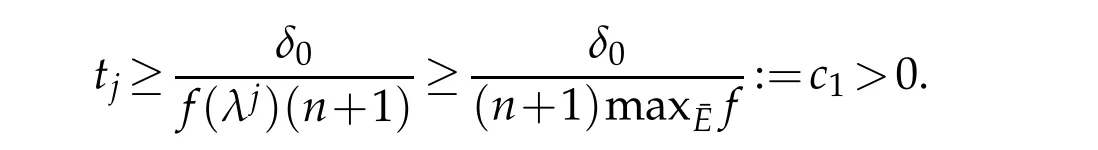
So our claim is correct and we may assumej=1.

Choose another compact setK1?Γ satisfyingK0??K1and dist(K1,?Γ)＞c0/2.Sincef∈C2(K1)we have,for eachi=1,...,n,when|h|＜c1dist(K0,?K1),

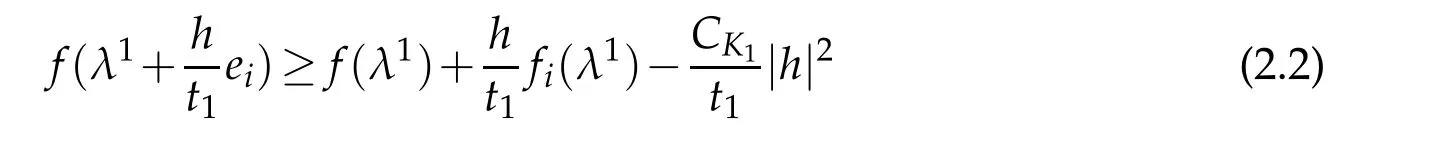
whereCK1=maxK1|D2f|/2.Therefore,by(2.2),

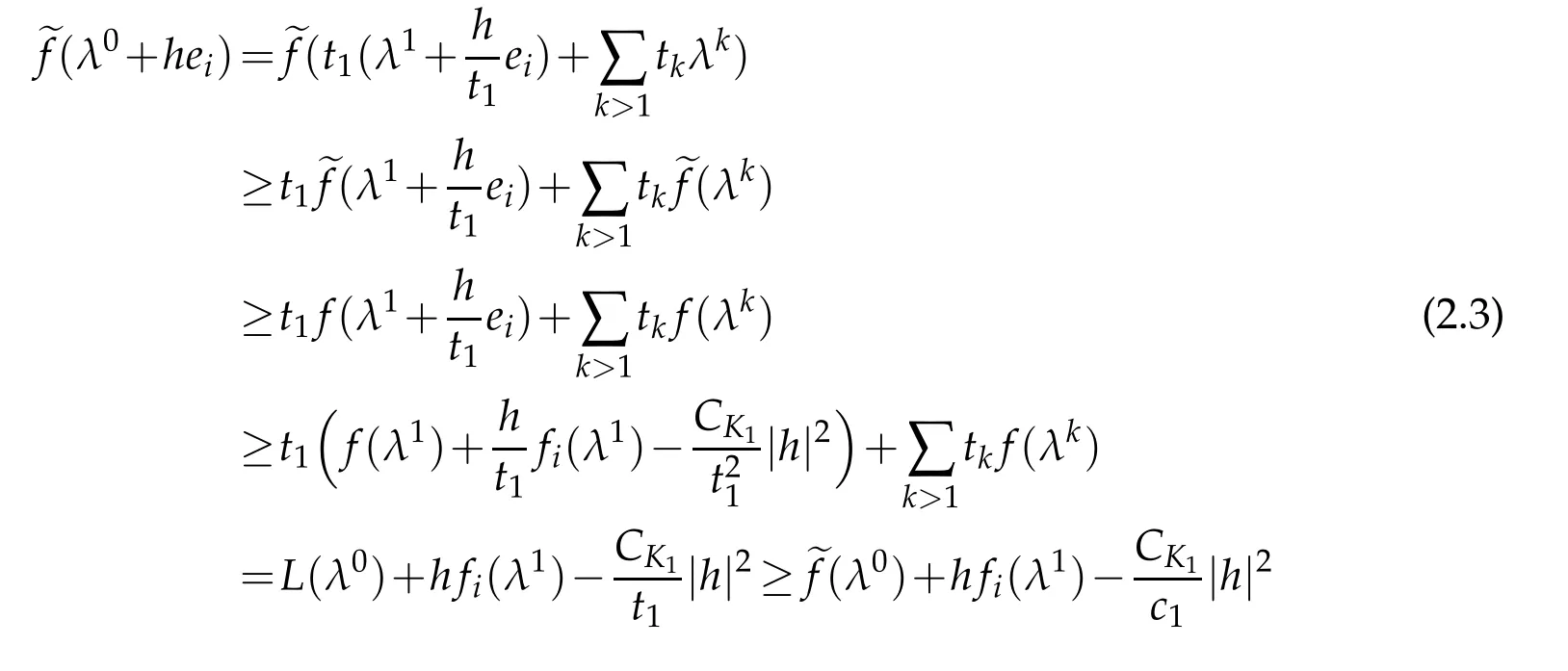
Now we note thatLis a supporting hyperplane tofatλ1which implies thatDf(λ1)=p0.On the other hand,

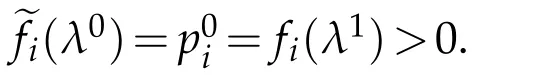
With some simple modifications ofthe above proof,we can show thatfor any compact setK?Γ,there exists a constantC0＞0 such that

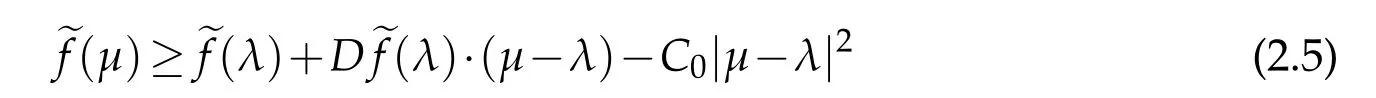
for anyμ,λ∈K.Therefore,it follows from the concavity of efthat ef∈C1,1(Γ).

The following lemma can be derived from(1.4)and the concavity of efwhich is crucial to our estimates.Its proof can be found in[7].

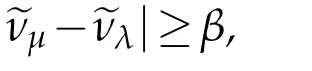
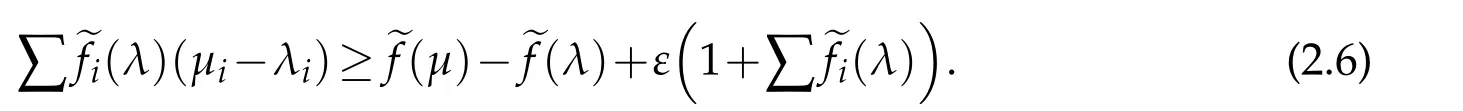
3 Global estimates for second derivatives

In this section we prove the following maximum principle under conditions of Theorem 1.1 or Theorem 1.2.

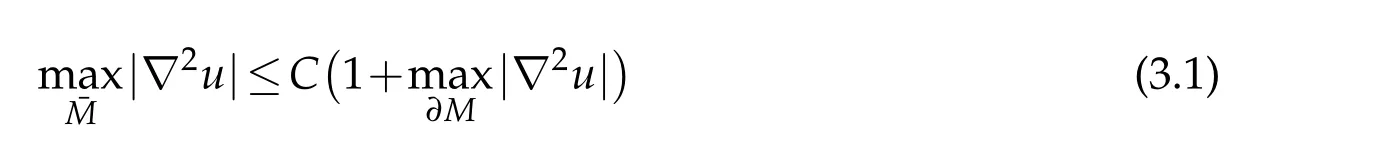
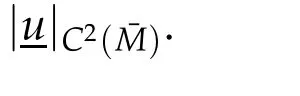
As in[4],we set

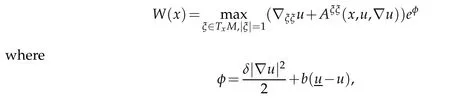
0＜δ?1?bare constants to be determined.Assume thatW(x0)=maxˉMWfor an interior pointx0∈M.Choose a smooth orthonormallocal framee1,...,enaboutx0such that?eiej=0 andUij:=?iju+Aij[u]is diagonal atx0.We may assume

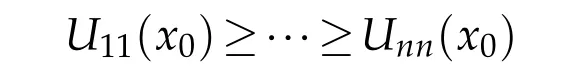
andW(x0)=U11(x0)eφ(x0).

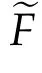
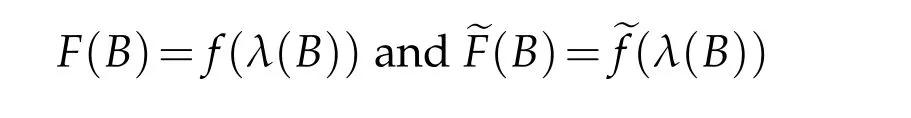
respectively for a symmetric matrixBwithλ(B)∈Γ;throughout the paper we shall use the notations

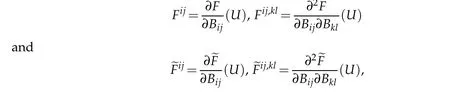
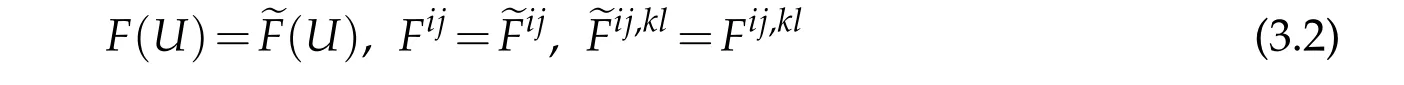
when|λ(U)|is sufficiently large.We see from(1.2)The matrix{Fij}has eigenvaluesf1,...,fnand is positive definite.Moreover,when{Uij}is diagonal so is{Fij},and we have

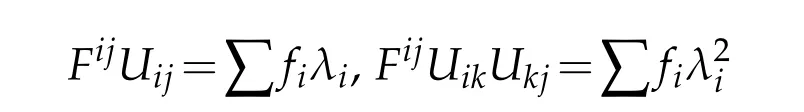
whereλ(U)=(λ1,...,λn).We see

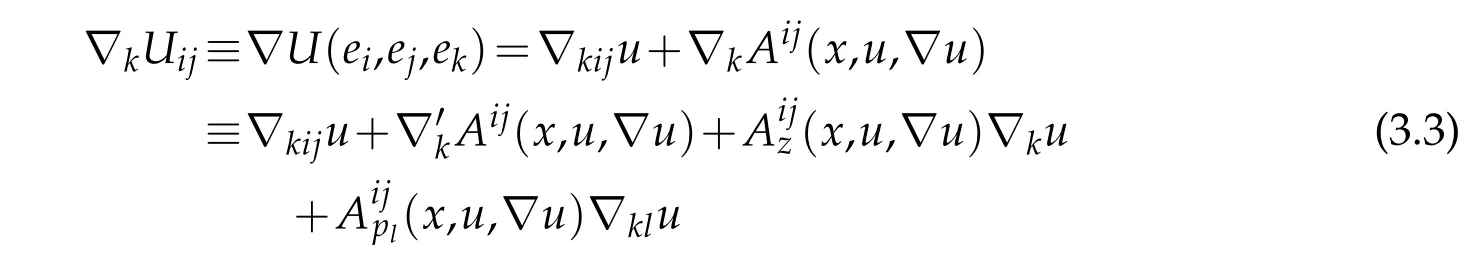
Let

and L be the linear operator locally defined by

whereAijpk≡Aijpk[u]≡Aijpk(x,u,?u),ψpk≡ψpk[u]≡ψpk(x,u,?u).We may assume that|λ(U(x0))|is sufficiently large such that(3.2)holds.Therefore,we can derive as in[5]using an idea of Urbas[10]that atx0,

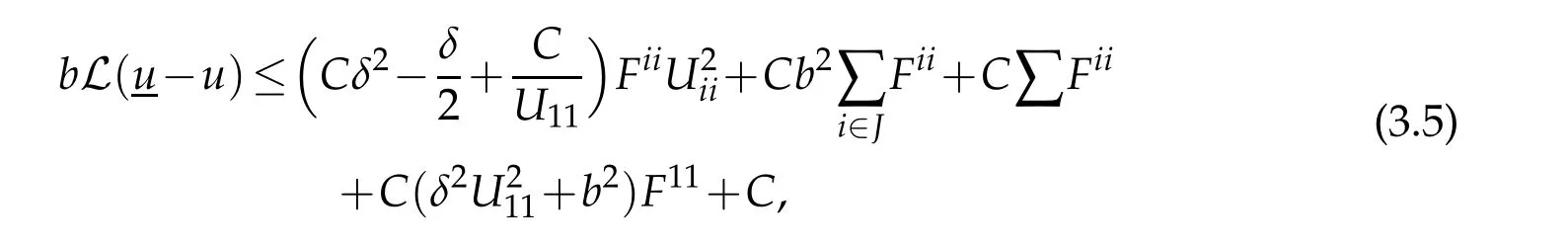
whereCmay depend on|u|C1(ˉM).

where 1=(1,...,1)∈Rn.

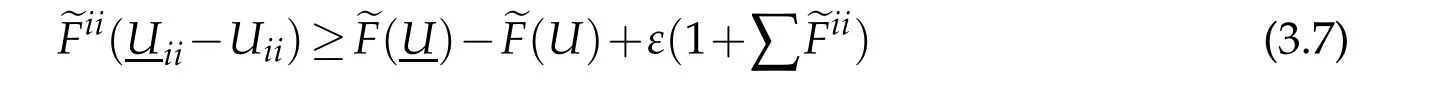
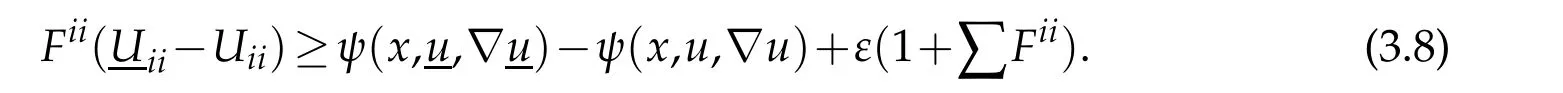
By(3.8),(1.5)and(1.6)we can derive as in[5]that

By(3.5),whenbis sufficiently large,

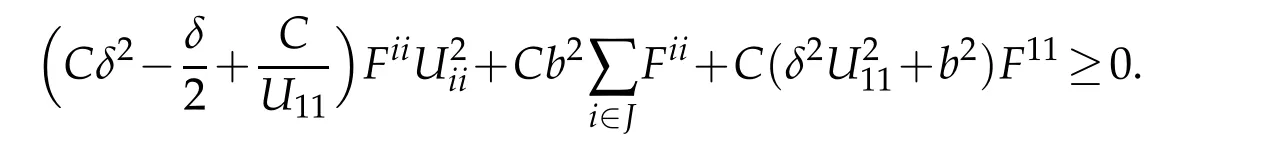
This implies a boundU11(x0)≤Cas otherwise the first term would be negative forδchosen sufficiently small,and|Uii|≥13U11fori∈J.

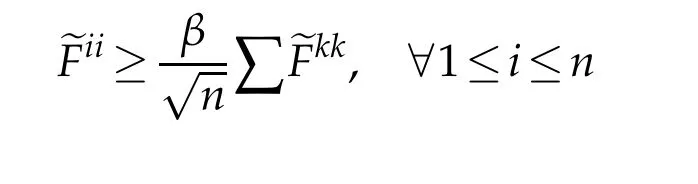
which means

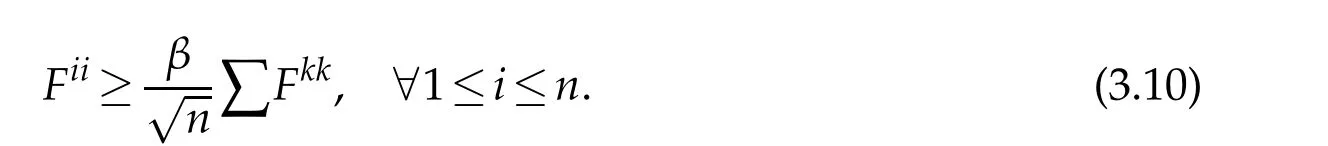
4 Boundary estimates for second derivatives

In this section we establish the estimatesforthe second orderderivatives on the boundary?M.As usual,the key step is to construct barrier functions.

For anyx0∈?M,we choose a smooth orthonormal local framee1,...,enaroundx0such thatenis the interior normal to?Malong the boundary when restricted to?M.

Sinceu?u=0 on?M,we have

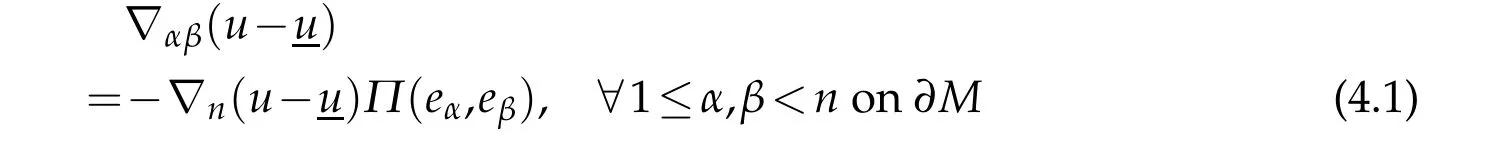
whereΠdenotes the second fundamental form of?M.Therefore,|?αβu|≤C,?1≤α,β＜non?M.

Letρ(x)andd(x)denote the distances fromx∈ˉMtox0and?M,respectively,and setMδ={x∈M:ρ(x)＜δ}.We may assumeρanddare smooth inMδby takingδsmall.

For the mixed tangential-normal and pure normal second derivatives atx0,we shall use the following barrier function as in[3],

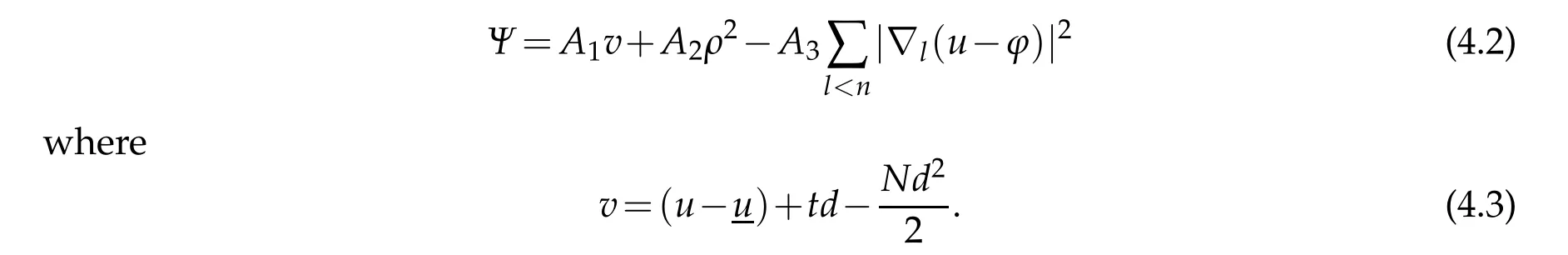
By differentiating the equation(1.1)and straightforward calculation,we have

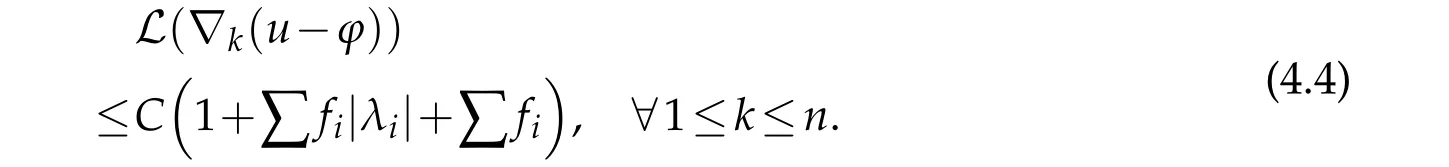
The following lemma is crucial to our proof.

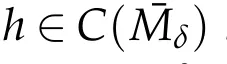
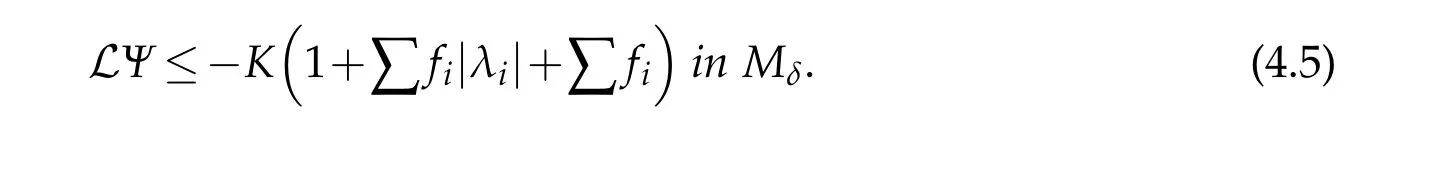
Proof.Forx∈Mδ,assume thatUijandFijare both diagonal atx.Letμ=λ(U(x))andλ=λ(U(x)).We first assume that|λ|≥R＞R0andRis sufficiently large.We consider two cases(a)|νμ?νλ|＜βand(b)|νμ?νλ|≥βas before.Note that(3.2)holds atxby(1.9)since|λ|＞R0.It follows that(3.10)holds in case(a)and(3.9)holds in case(b).So we can chooseA1?A2?A3?1 as in[6]to obtain that(see(3.23)in[6])

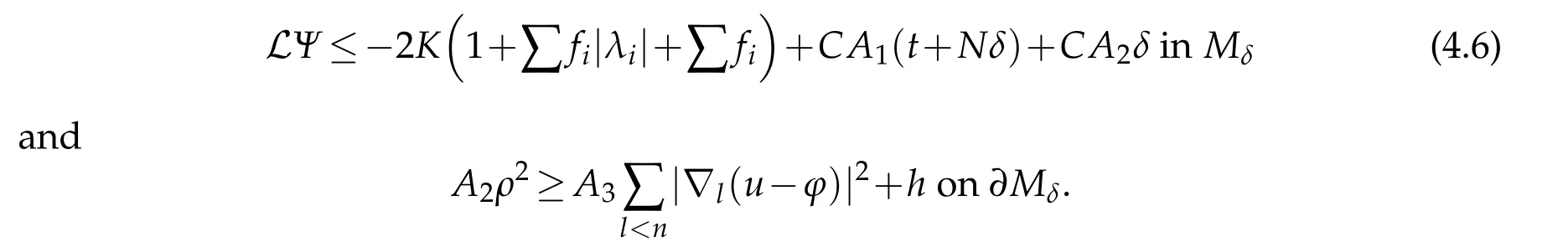
Now we consider the case that|λ|≤R.By(1.10)and(1.2),we have

for some positive constantCRdepending onR.Because?d≡1,we have

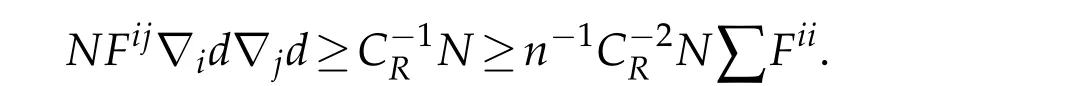
It follows that

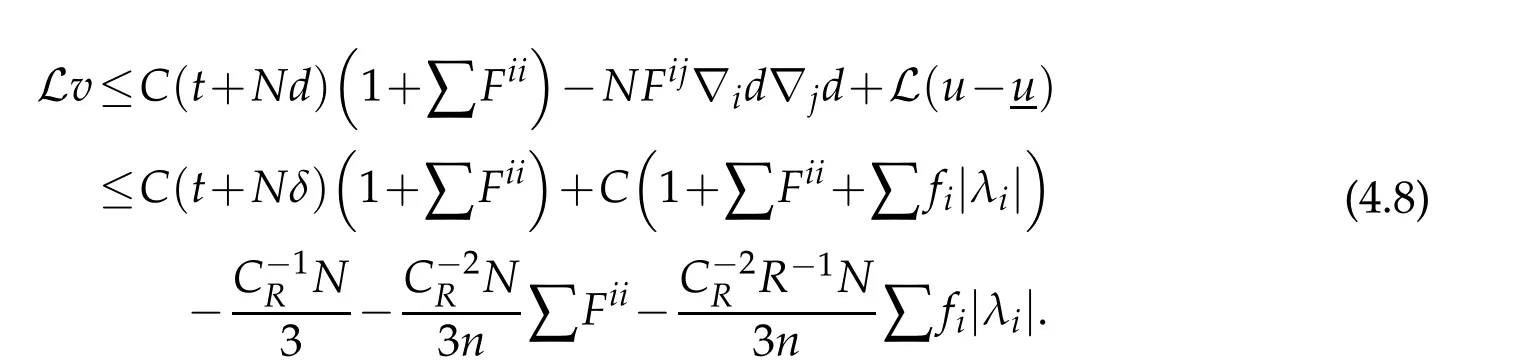
Therefore,choosingNsufficiently large,(4.6)is also valid forCdepending onRand|u|C1(ˉM).Finally,we may choose smallertandδsuch that(4.5)holds and thatv≥0 onˉMδ.The proof of Lemma 4.1 is completed.

For fixed 1≤α＜n,by Lemma 4.1 we see

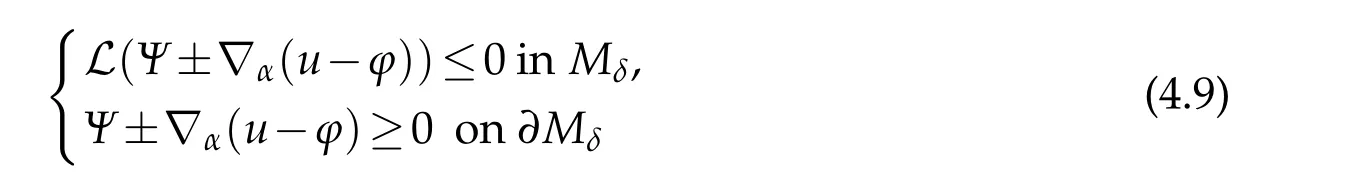
by choosingA1?A2?A3?1.By the maximum principle we haveΨ±?α(u??)≥0 inMδand therefore

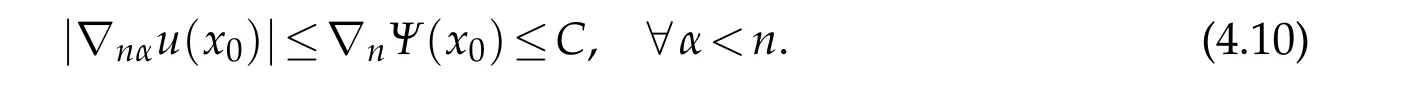
It suffices to obtain an upper bound of?nnuon?Msince△u≥?C.The proof is similar to that of[5],so we only provide a sketch here.

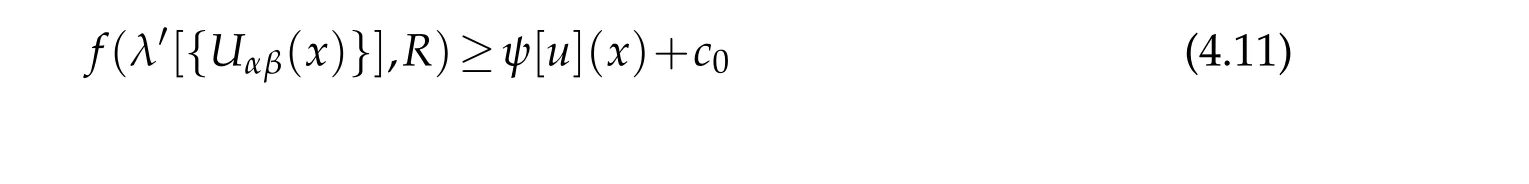
Using an idea of Trudinger[9]we show that there are uniform constantsc0,R1such that for allR＞R1,(λ′[{Uαβ(x)}],R)∈Γ and for anyx∈?M,whereλ′[{Uαβ}]=(λ′1,···,λ′n?1)denotes the eigenvalues of the(n?1)×(n?1)matrix{Uαβ}(1≤α,β≤n?1),andψ[u]=ψ(·,u,?u).From(4.11)we can derive an upper bound ofUnnon?Mby Lemma 1.2 in[1].

ForR＞ 0 and a symmetric(n?1)2matrix{rαβ}with(λ′[{rαβ}],R)∈ Γ whenRis sufficiently large,define

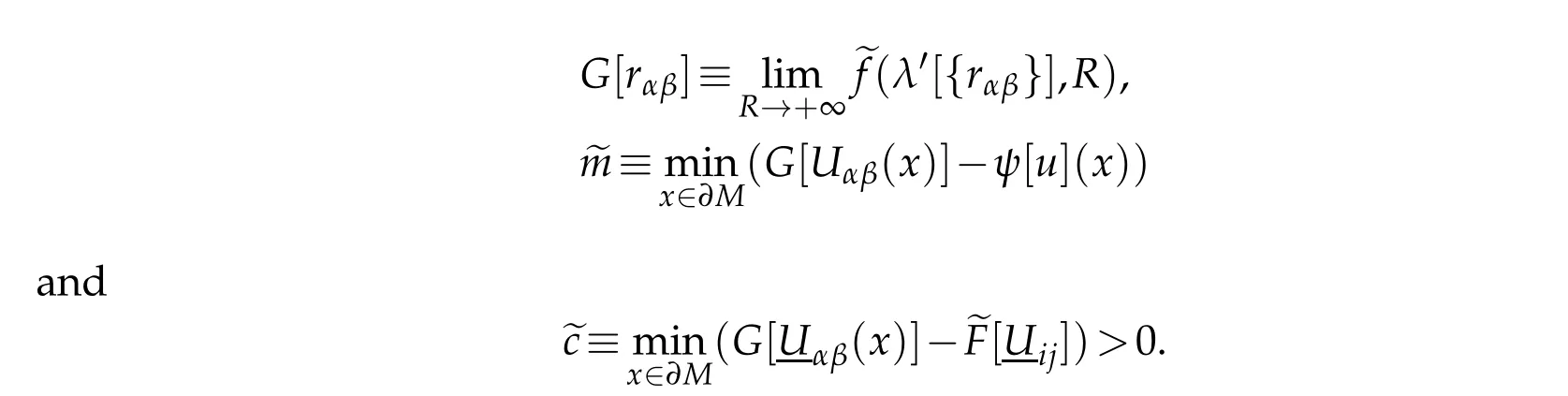
We wish to show em＞0 and we may assume em＜ec/2(otherwise we are done).Suppose emis achieved at a pointx0∈?M.Letσαβ=〈?αeβ,en〉and note thatσαβ=Π(eα,eβ)on?M.By(4.1)and the concavity ofG,there exists a positive semidefinite matrix{Gαβ0}such that atx0,

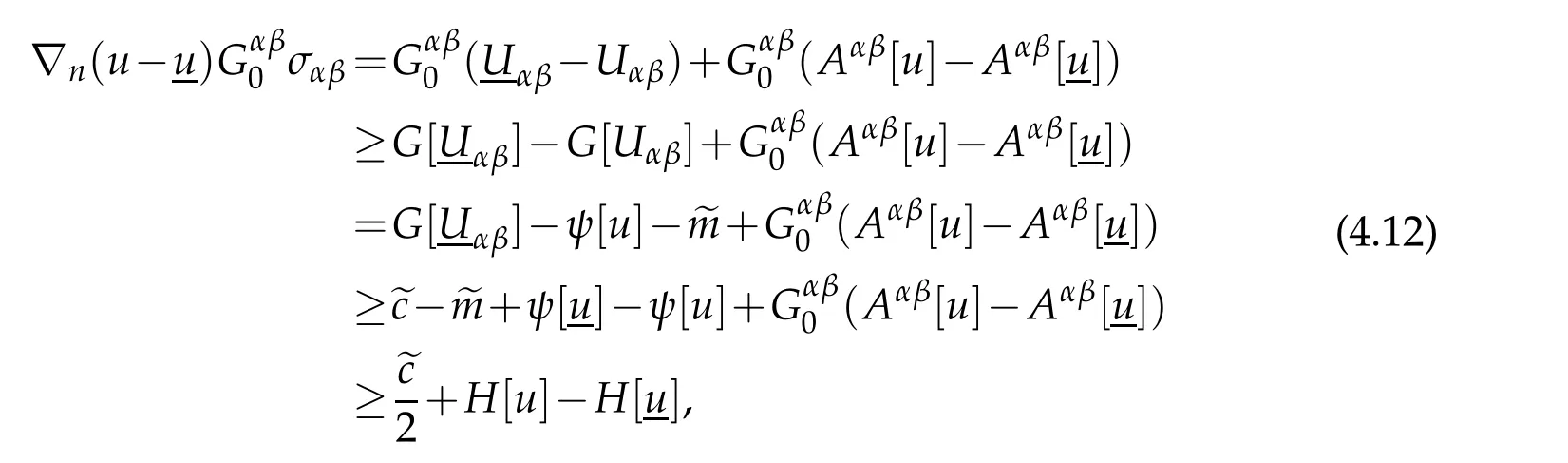
Define

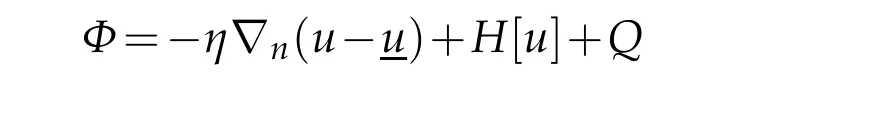
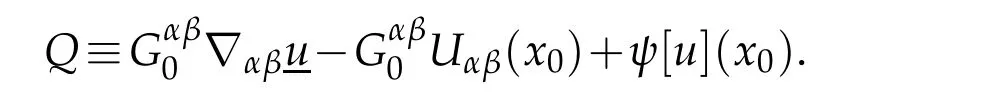
By(4.1)and the concavity ofGagain,we see that

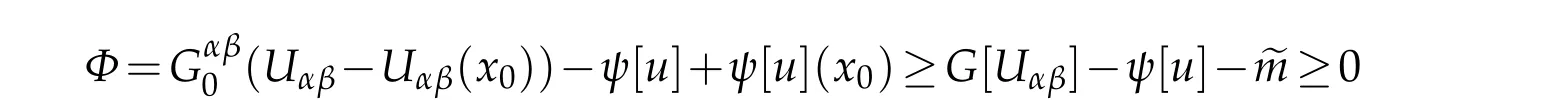
on?Mnearx0.ObviouslyΦ(x0)=0.

We can derive from(4.4)and(1.5)as in[5]that

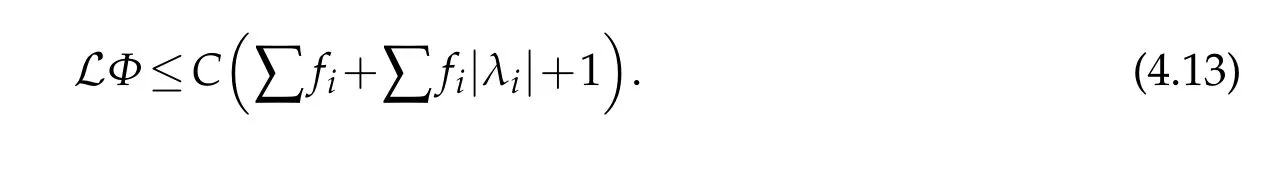
Applying Lemma 4.1 again forA1?A2?A3?1 we have

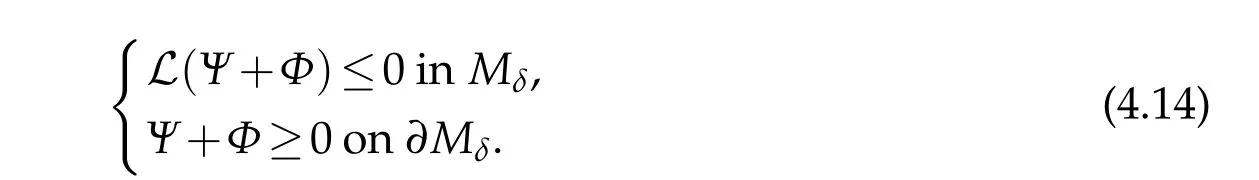
By the maximum principle,Ψ+Φ≥0 inMδ.Thus?nΦ(x0)≥??nΨ(x0)≥?C.

Thus,we have(see[5]for details)

Therefore,we obtain anaprioriupperbound for all eigenvalues of{Uij(x0)}which means thatλ[{Uij(x0)}]is contained in a compact subset of Γ by(1.10).So

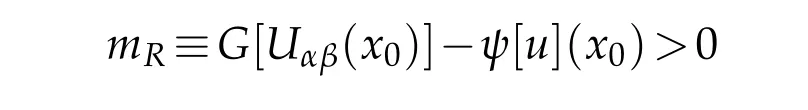
whenRis sufficiently large.It follows that

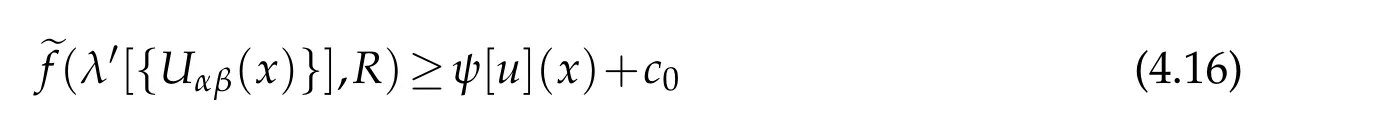
for anyx∈?M.This proves(4.11)by(1.9).Then we obtain the boundary estimates for all second order derivatives.

5 The gradient estimates

In this section we give some theorems about the gradient estimates.As in[6],we assume the following growth conditions throughout the section

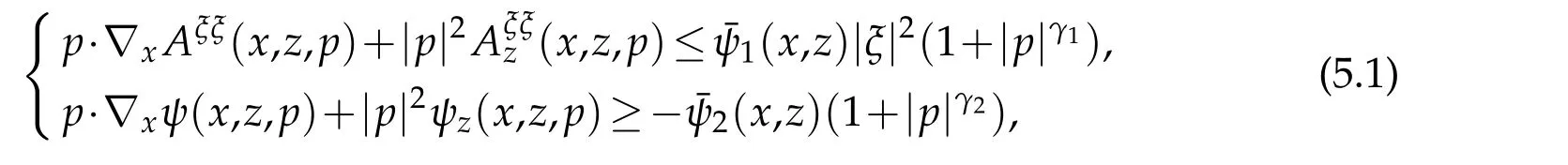
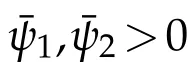
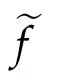
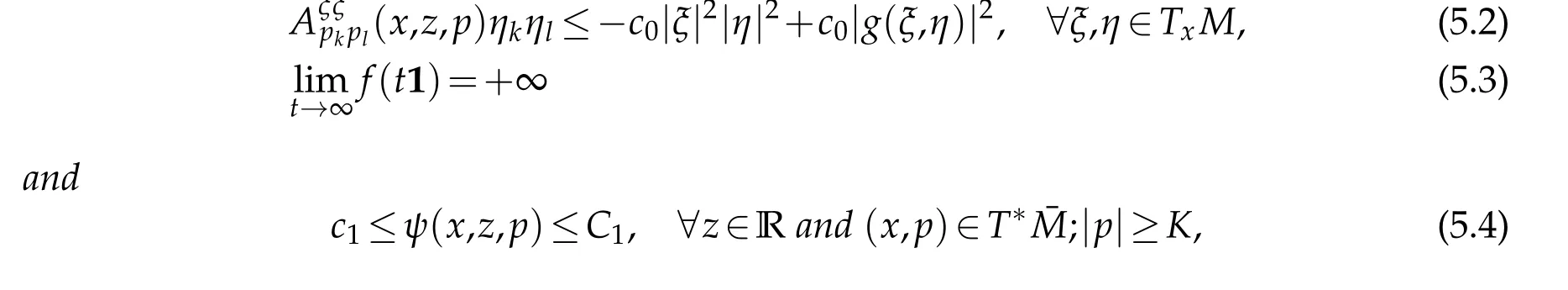
where1=(1,...,1)∈Rn.Suppose γ1＜4,γ2=2in(5.1),and that there is an admissible function u∈C2(ˉM).Then

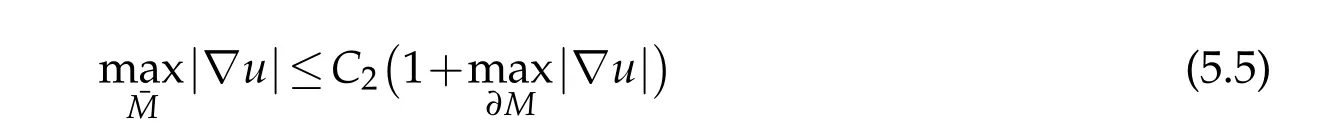
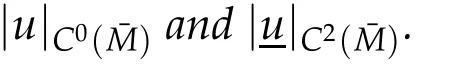
Proof.As in[6],letw=|?u|andφa positive function to be determined.Suppose the functionwφ?aachieves a positive maximum at an interior pointx0∈Mwherea＜1 is a positive constant.Choose a smooth orthonormal local framee1,...,enaboutx0such that?eiej=0 atx0and{Uij(x0)}is diagonal.

Using the same arguments of Theorem 4.1 in[6],we can derive atx0,

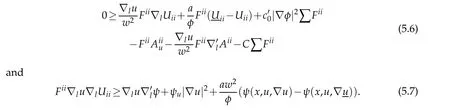
Now we considertwo cases as before:(i)|λ|≥RforRsufficiently large and(ii)|λ|＜R,whereλ=λ(U(x0)).

In case(i),we may assumeR＞R0so that(3.2)holds.Therefore,we can get a bound|?u(x0)|≤Cas in[6].

For case(ii)we note that(4.7)holds by(1.2),(1.10)and(5.4).Therefore,by(5.1),(5.6),(5.7)and(4.7),we have

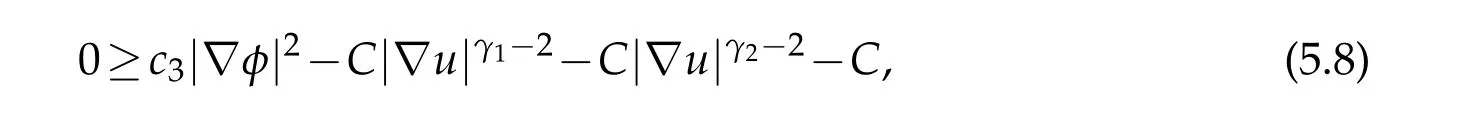
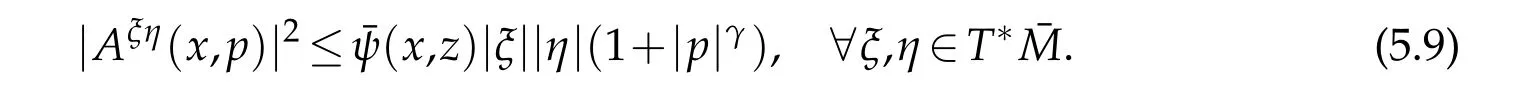
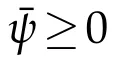
Proof.We first assume|λ|≥RforRsufficiently large as before.Again by(1.9),(3.2)holds.So the bound of|?u(x0)|can be derived as Theorem 4.2 in[6].

If|λ|≤R,we note that(4.7)holds and that,by(1.5),

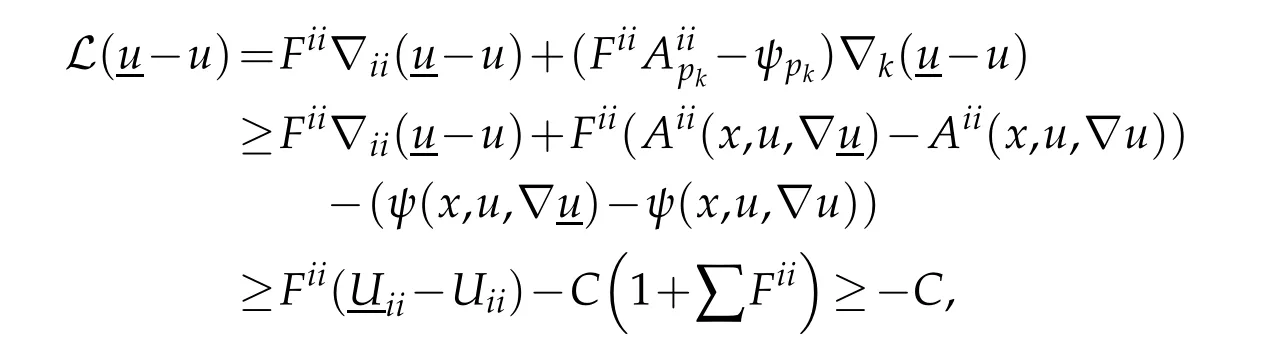
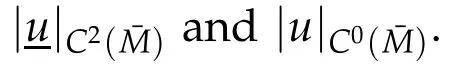
The following Theorem 5.3 was proved in[6]under conditions

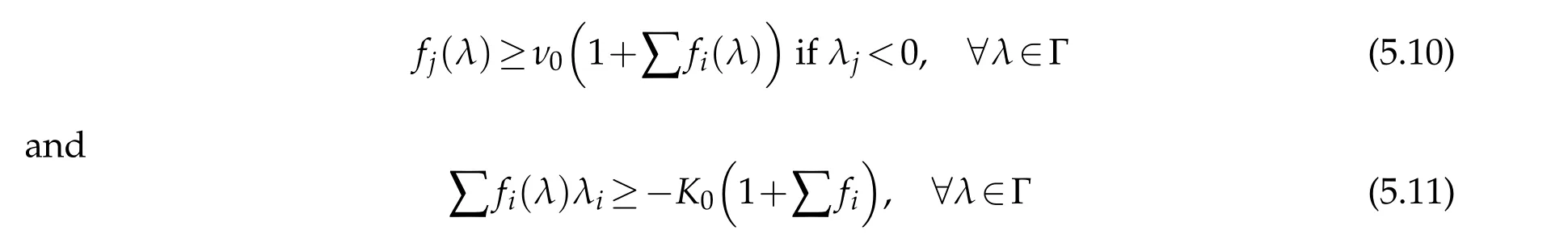
for some constantsν0＞0 andK0≥0.

Theorem 5.3.Suppose that(1.2),(5.10)and(5.11)hold,γ1,γ2＜4in(5.1),and that

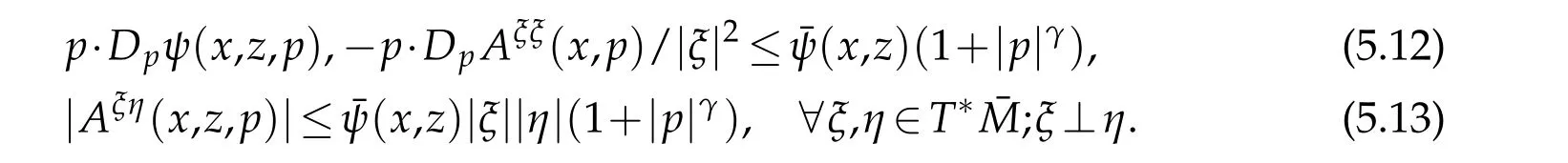
for some functionˉψ≥0and constant γ∈(0,2).There exists a constant C1depending on|u|C0(ˉM)and other known data such that(5.5)holds.

Acknowledgments

The author is supported by the Fundamental Research Funds for the Central Universities and Program for Innovation Research of Science in Harbin Institute of Technology,No.61509066.

[1]L.A.Caffarelli,L.Nirenberg and J.Spruck.The Dirichlet problem for nonlinear secondorder elliptic equations III:Functions of eigenvalues of the Hessian.Acta Math.,155:261-301,1985.

[2]G.De Philippis and A.Figalli.Optimal regularity of the convex envelope.Trans.Amer.Math.Soc.,367:4407-4422,2015.

[3]B.Guan.Second order estimates and regularity for fully nonlinear elliptic equations on Riemannian manifolds.Duke Math.J.,163:1491-1524,2014.

[4]B.Guan.The Dirichlet problem for fully nonlinear elliptic equations on Riemannian manifolds.ArXiv:1403.2133.

[5]B.Guan and H.-M.Jiao.Second order estimates for Hessian type fully nonlinear elliptic equations on Riemannian manifolds.Calc.Var.Partial Differ.Eqns.,2015,doi:10.1007/s00526-015-0880-8.

[6]B.Guan and H.-M.Jiao.The Dirichlet problem for Hessian type elliptic equations on Riemannian manifolds.To appear in Discrete Cont.Dyn-A.

[7]B.Guan,S.-J.Shi and Z.-N.Sui.On estimates for fully nonlinear parabolic equations on Riemannian manifolds.ArXiv:1409.3633.

[8]C.E.Guti′errez.The Monge-Amp`ere equation,Birkh¨auser.Boston,Basel,Berlin,2001.

[9]N.S.Trudinger.On the Dirichlet problem for Hessian equations.Acta Math.,175:151-164,1995.

[10]J.Urbas.Hessian equations on compact Riemannian manifolds.Nonlinear Problems in Mathematical Physics and Related Topics II,367-377,Kluwer/Plenum,New York,2002.

18 March,2015;Accepted 16 July,2015

?Corresponding author.Email address:jiao@hit.edu.cn(H.Jiao)