ON CONFORMABLE NABLA FRACTIONAL DERIVATIVE ON TIME SCALES

ZHAO Da-fang,YOU Xue-xiao,HU Chang-song

(School of Mathematics and Statistics,Hubei Normal University,Huangshi 435002,China)

ON CONFORMABLE NABLA FRACTIONAL DERIVATIVE ON TIME SCALES

ZHAO Da-fang,YOU Xue-xiao,HU Chang-song

(School of Mathematics and Statistics,Hubei Normal University,Huangshi 435002,China)

In this paper,we introduce and investigate the concept of conformable nabla fractional derivative on time scales.By using the theory of time scales,we obtain some basic properties of the conformable nabla fractional derivative,which extend and improve both the results in[9,10]and the usual nabla derivative.

conformable nabla fractional derivative;nabla derivative;time scales

2010 MR Subject Classification:26A33;26E70

Document code:AArticle ID:0255-7797(2016)06-1142-07

1　Introduction

Fractional Calculus is a generalization of ordinary differentiation and integration to arbitrary(non-integer)order.The subject is as old as the calculus of differentiation and goes back to times when Leibniz,Gauss,and Newton invented this kind of calculation.During three centuries,the theory of fractional calculus developed as a pure theoretical field,useful only for mathematicians.Nowadays,the fractional calculus attracts many scientists and engineers.There were several applications of this mathematical phenomenon in mechanics, physics,chemistry,control theory and so on[1-8].

Recently,the authors in[9]defined a new well-behaved simple fractional derivative called the conformable fractional derivative depending just on the basic limit definition of the derivative.Especialy,in[10],Nadia Benkhettou,Salima Hassani and Delfim Torres introduced a conformable time-scale fractional derivative,which providing a natural extension of the conformable fractional derivative.In this paper,we define the conformable nabla fractional derivative on time scales,which give another type of generalization of the conformable fractional derivative and the usual nabla derivative[11-14].

2　Preliminaries

A time scale T is a nonempty closed subset of real numbers R with the subspace topology inherited from the standard topology of R.For a,b∈T we define the closed interval[a,b]Tby[a,b]T={t∈T:a≤t≤b}.For t∈T we define the forward jump operator σ by σ(t)=inf{s＞t:s∈T},where inf?=supT,while the backward jump operator ρ is defined by ρ(t)=sup{s＜t:s∈T},where sup?=inf T.

If σ(t)＞t,we say that t is right-scattered,while if ρ(t)＜t,we say that t is leftscattered.If σ(t)=t,we say that t is right-dense,while if ρ(t)=t,we say that t is left-dense.A point t∈T is dense if it is right and left dense;isolated if it is right and left scattered.The forward graininess functionμ(t)and the backward graininess function η(t) are defined byμ(t)=σ(t)-t,η(t)=t-ρ(t)for all t∈T,respectively.If supT is finite and left-scattered,then we define Tk:=TsupT,otherwise Tk:=T;if inf T is finite and right-scattered,then Tk:=Tinf T,otherwise Tk:=T.We set

A function f:T→R is nabla(?)differentiable at t∈Tkif there exists a number f?(t)such that,for each ε＞0,there exists a neighborhood U of t such that

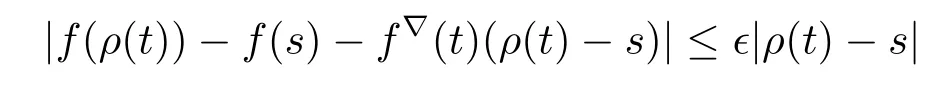
for all s∈U.We call f?(t)the?-derivative of f at t.Throughout this paper,α∈(0,1].

3　Conformable Nabla Fractional Derivative

Definition 3.1 Let T be a time scale and α∈(0,1].A function f:T→R is conformable?-fractional differentiable of order α at t∈Tkif there exists a number Tα(f?)(t) such that,for each ε＞0,there exists a neighborhood U of t such that

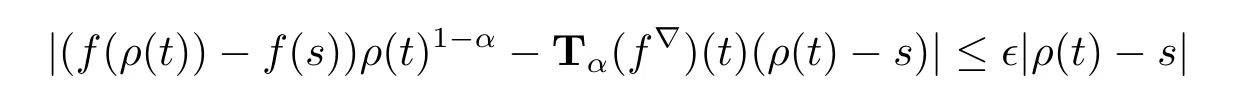
for all s∈U.We call Tα(f?)(t)the conformable?-fractional derivative of f of order α at t and we say that f is conformable?-fractional differentiable if f is conformable?-fractional differentiable for all t∈Tk.

Theorem 3.2 Let T be a time scale,t∈Tkand α∈(0,1].Then we have the following:

(i)If f is conformal?-fractional differentiable of order α at t,then f is continuous at t.

(ii)If f is continuous at t and t is left-scattered,then f is conformable?-fractional differentiable of order α at t with

(iii)If t is left-dense,then f is conformable?-fractional differentiable of order α at t if and only if the limitexists as a finite number.In this case,

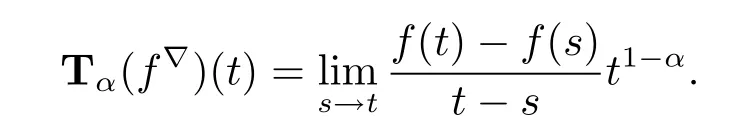
(iv)If f is conformal?-fractional differentiable of order α at t,then

Proof (i)The proof is easy and will be omitted.

(ii)Assume that f is continuous at t and t is left-scattered.By continuity,

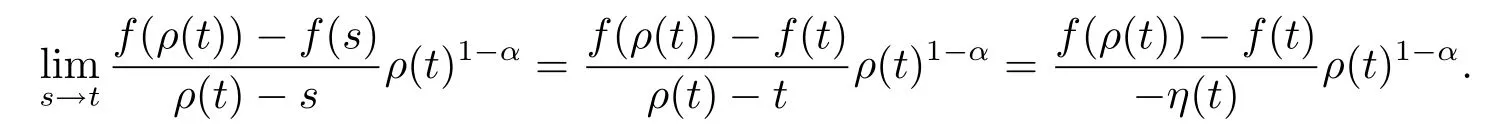
Hence given ε＞0,there exists a neighborhood U of t such that

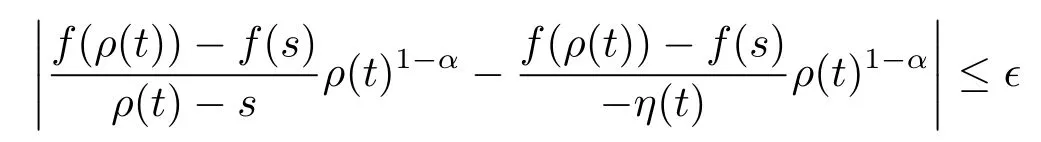
for all s∈U.It follows that

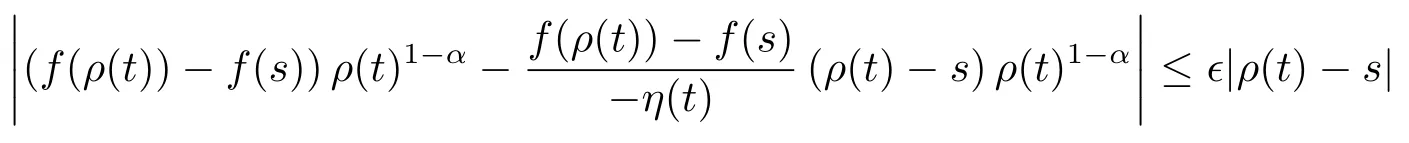
for all s∈U.Hence we get the desired result

(iii)Assume that f is conformable?-fractional differentiable of order α at t and t is right-dense.Then for each ε＞0,there exists a neighborhood U of t such that

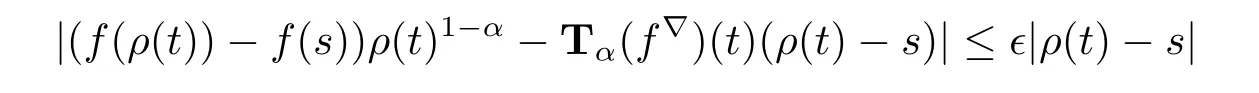
for all s∈U.Since ρ(t)=t we have thatfor all s∈U.It follows thatHence we get the desired result.

On the other hand,if the limitexists as a finite number and is equal to J,then for each ε＞0,there exists a neighborhood U of t such that

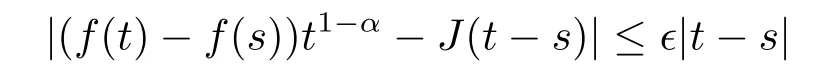
for all s∈U.Since t is right-dense,we have that

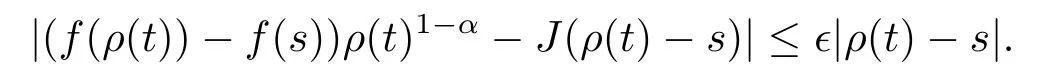
Hence f is conformable?-fractional differentiable at t and Tα(f?)(t)=

(iv)If t is left-dense,then η(t)=0 and we have that

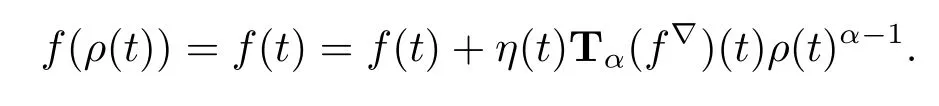
If t is left-scattered,then ρ(t)＜t,then by(ii)

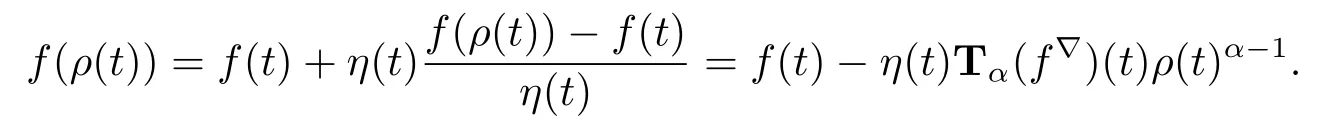
Corollary 3.3Again we consider the two cases T=R and T=Z.

(i)If T=R,then f:R→R is conformable?-fractional differentiable of order α at t∈R if and only if the limitexists as a finite number.In this case,

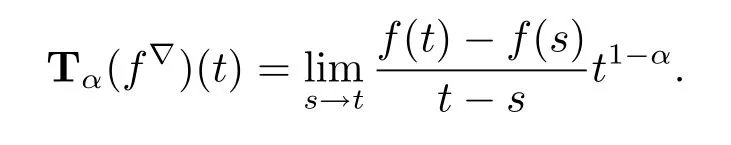
If α=1,then we have that Tα(f?)(t)=f?(t)=f＇(t).

(ii)if T=Z,then f:Z→R is conformable?-fractional differentiable of order α at t∈Z with

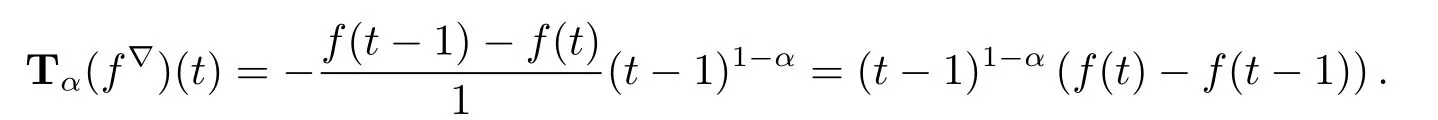
If α=1,then we have that Tα(f?)(t)=f(t)-f(t-1)=?f(t),where?is the usual backward difference operator.

Example 3.4If f:T→R is defined by f(t)=C for all t∈T,where C∈R is constant,then Tα(f?)(t)≡0.

(ii)if f:T→R is defined by f(t)=t for all t∈T,then Tα(f?)(t)=ρ(t)1-α.If α=1, then Tα(f?)(t)≡1.

Example 3.5If f:T→R is defined by f(t)=t2for all t∈T:=from Theorem 3.2(ii)we have that f is conformable?-fractional differentiable of order α at t∈T with

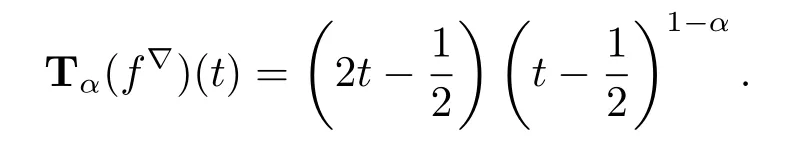
Theorem 3.6 Assume f,g:T→R are conformable?-fractional differentiable of order α at t∈Tk,then

(i)for any constant λ1,λ2,the sum λ1f+λ2g:T→R is conformable?-fractional differentiable of order α at t with Tα((λ1f+λ2g)?)(t)=λ1Tα(f?)(t)+λ2Tα(g?)(t);

(ii)if f and g are continuous,then the product fg:T→R is conformable?-fractional differentiable of order α at t with

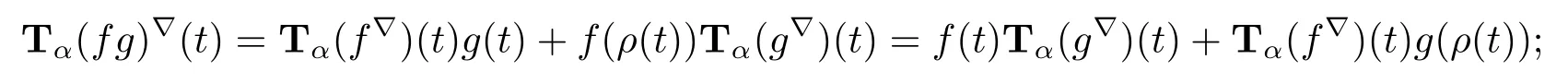
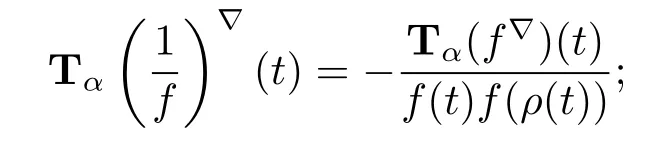
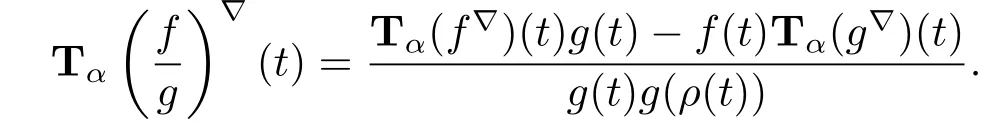
Proof (i)The proof is easy and will be omitted.

(ii)Let 0＜ε＜1.Define

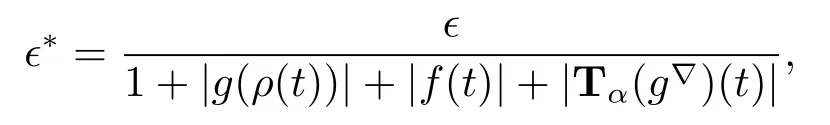
then 0＜∈?＜1.f,g:T→R are conformable?-fractional differentiable of order α at t. Then there exists neighborhoods U1and U2of t with

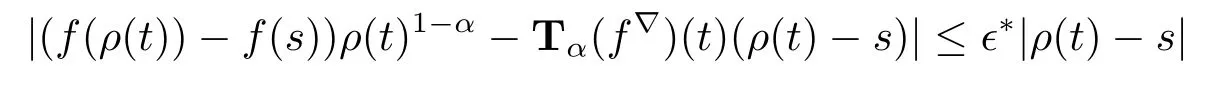
for all s∈U1and

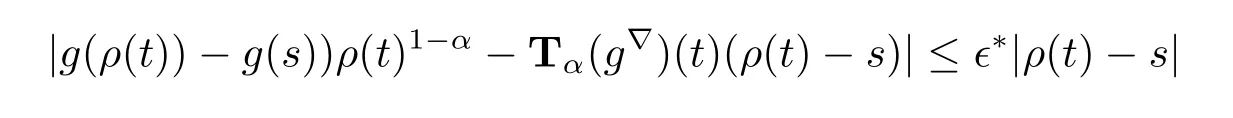
for all s∈U2.

From Theorem 3.2(i),there exists neighborhoods U3of t with|f(t)-f(s)|≤∈?for all s∈U3.

Let U=U1∩U2∩U3.Then we have for all s∈U

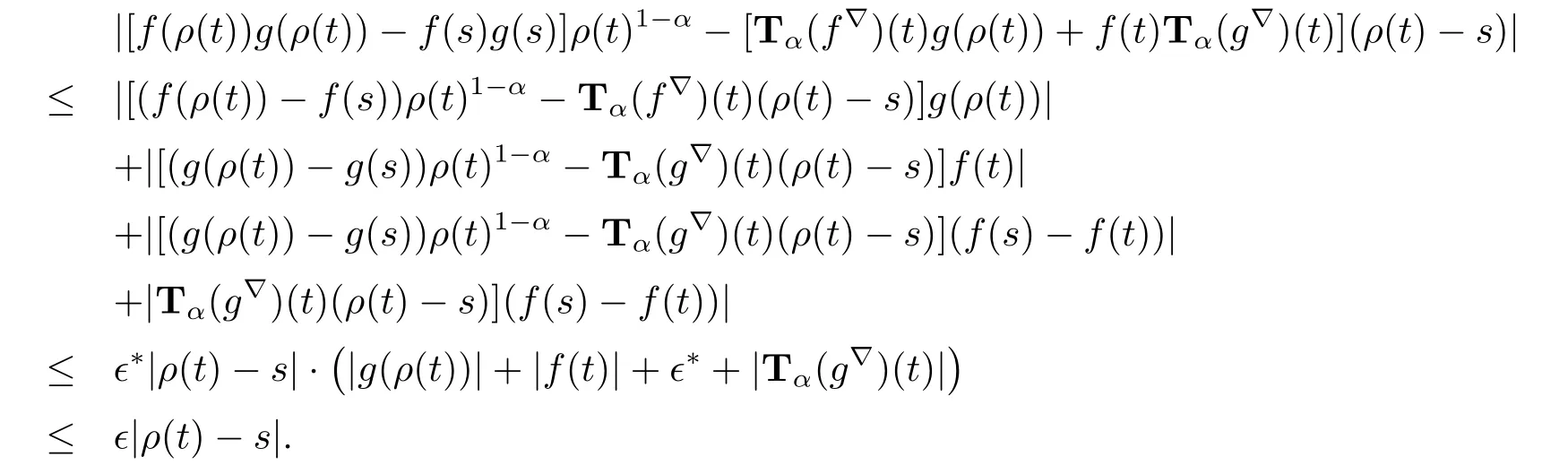
Thus Tα(fg)?(t)=f(t)Tα(g?)(t)+Tα(f?)(t)g(ρ(t)).The other product rule formula follows by interchanging the role of functions f and g.

(iii)From Example 3.4,we have that Tα(t)=Tα(1)?(t)=0.Therefore

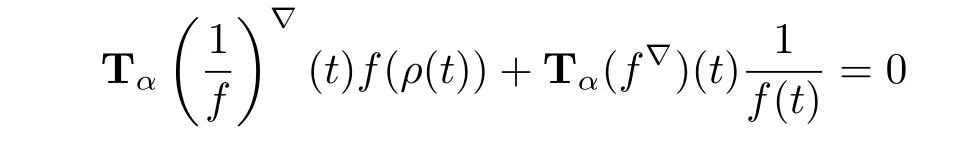
and consequently Tα(

(iv)We use(ii)and(iii)to calculate

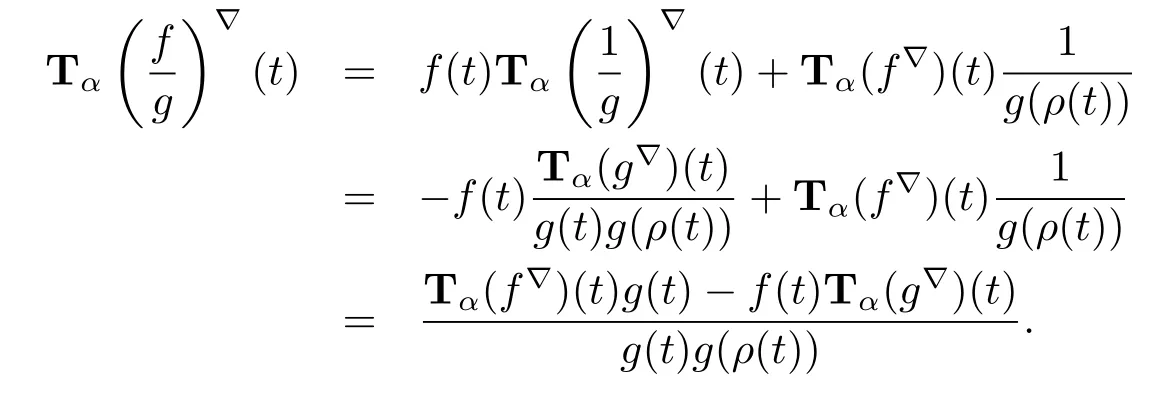
Theorem 3.7 Let c be constant and m∈N.

(i)For f defined by f(t)=(t-c)m,we have that

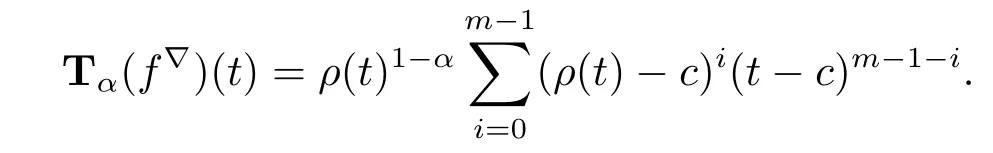
Proof (i)We prove the first formula by induction.If m=1,then f(t)=t-c,and clearly Tα(f?)(t)=ρ(t)1-αholds by Example 3.4 and Theorem 3.6(i).Now we assume that

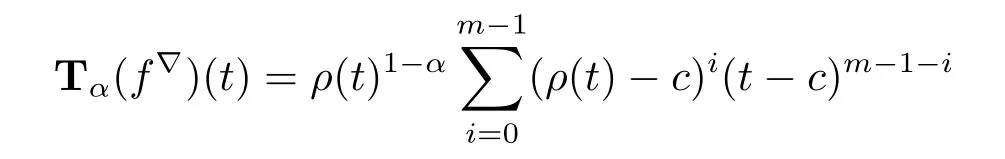
holds for f(t)=(t-c)mand let F(t)=(t-c)m+1=(t-c)f(t).We use Theorem 3.6(ii) to obtain

Hence part(i)holds.

Example 3.8 If f:T→R is defined by f(t)=we have that f is conformable?-fractional differentiable of order α at t∈T with

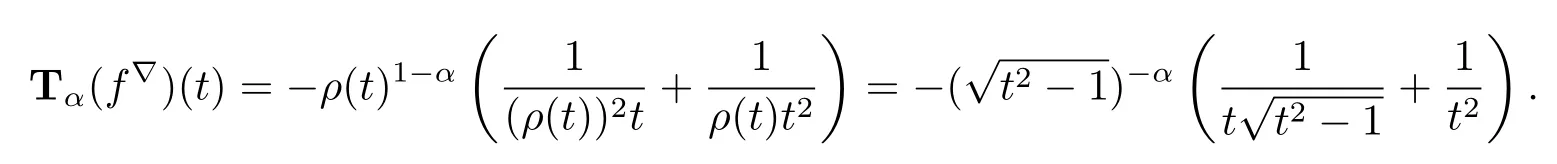
References

[1]Miller K,Ross B.An introduction to the fractional calculus and fractional differential equations[M]. New York:Wiley,1993.

[2]Oldham K B,Spanier J.The fractional calculus[M].New York,London:Academic Press,1974.

[3]Podlubny I.Fractional differential equations[M].San Diego:Academic Press,1999.

[4]Herrmann R.Fractional calculus:an introduction for physicists[M].Singapore:World Sci.,2014.

[5]Sabatier J,Agrawal O P,Machado J A T.Advances in fractional calculus:theoretical developments and applications in physics and engineering[M].Berlin:Springer,2007.

[7]Meilanov R P,Magomedov R A.Thermodynamics in fractional calculus[J].J.Engin.Phys.Thermophys.,2014,87(6):1521-1531.

[8]Carpinteri A,Cornetti P,Alberto Sapora.Nonlocal elasticity:an approach based on fractional calculus[J].Meccanica,2014,49(11):2551-2569.

[9]Khalil R,Al Horani M,Yousef A,Sababheh M.A new definition of fractional derivative[J].J. Comput.Appl.Math.,2014,264:57-66.

[10]Benkhettou N,Hassani S,Torres D F M.A conformable fractional calculus on arbitrary time scales[J].J.King Saud Univ.Sci.,2016,28:93-98.

[11]Hilger S.Ein Makettenkalkl mit Anwendung auf Zentrumsmannigfaltigkeiten[D].Wurzburg:Universtat Wurzburg,1988.

[12]Hilger S.Analysis on measure chains-a unified approach to continuous and discrete calculus[J]. Results Math.,1990,18:18-56.

[13]Bohner M,Peterson A.Dynamic equations on time scales:an introduction with applications[M]. Boston:Birkhauser,2001.

[14]Bohner M,Peterson A.Advances in dynamic equations on time scales[M].Boston:Birkhauser,2004.

[15]Zhao Dafang,Ye Guoju.C-integral and denjoy-C integral[J].Comm.Korean.Math.Soc.,2007, 22(1):27-39.

[16]Zhao Dafang,Ye Guoju.On strong C-integral of Banach-valued functions[J].J.Chungcheong Math. Soc.,2007,20(1):1-10.

[17]Zhao Dafang.On the C1-integral[J].J.Math.,2011,31(5):823-828.

[18]Zhao Dafang,Li Biwen.A note on the C-integral[J].J.Math.,2011,31(4):594-598.

關(guān)于時(shí)標(biāo)上的適應(yīng)Nabla分?jǐn)?shù)階導(dǎo)數(shù)

趙大方,游雪肖,胡長(zhǎng)松

(湖北師范大學(xué)數(shù)學(xué)與統(tǒng)計(jì)學(xué)院,湖北黃石435002)

本文研究了時(shí)標(biāo)上的適應(yīng)Nabla分?jǐn)?shù)階導(dǎo)數(shù)的問(wèn)題.利用時(shí)標(biāo)理論,獲得了關(guān)于適應(yīng)Nabla分?jǐn)?shù)階導(dǎo)數(shù)的若干重要性質(zhì).這些結(jié)果推廣并改進(jìn)了文獻(xiàn)[9,10]中的有關(guān)結(jié)論以及一般Nabla導(dǎo)數(shù)的性質(zhì).

適應(yīng)Nabla分?jǐn)?shù)階導(dǎo)數(shù);Nabla導(dǎo)數(shù);時(shí)標(biāo)

MR(2010)主題分類號(hào):26A33;26E70O174.1

?date:2016-01-22Accepted date:2016-04-22

Supported by Educational Commission of Hubei Province of China (Q20152505).

Biography:Zhao Dafang(1982-),male,born at Linyi,Shandong,master,major in Henstock integral theory.