RECOLLEMENT OF COHERENT FUNCTOR CATEGORIES OVER TRIANGULATED CATEGORIES

LIN Ji

(School of Mathematics and Statistics,Fuyang Teachers Collage,Fuyang 236037,China)

RECOLLEMENT OF COHERENT FUNCTOR CATEGORIES OVER TRIANGULATED CATEGORIES

LIN Ji

(School of Mathematics and Statistics,Fuyang Teachers Collage,Fuyang 236037,China)

The relationship between recollement of triangulated category D and recollement of its coherent functor category A(D)is studied.It is shown that the recollement of D induces the prerecollement of A(D)and the necessary and sufficient condition for it to be a recollement is that the recollement of D is split.Furthermore,we get the result that the recolloment of D could induce the prerecollement of

recollement;triangulated category;coherent functor category;abelian category

2010 MR Subject Classification:18E10;18E30;18E35

Document code:AArticle ID:0255-7797(201606-1201-08

1　Introduction

The notion of recollement of triangulated categories was introduced by Beilinson,Bernstein and Deligne[1]in connection with derived categories of sheaves of topological spaces in 1982.Besides the recollement of triangulated categories,MacPherson and Vilonen[2] introduced recollement of abelian categories,it first appeared as an inductive step in the construction of perverse sheaves.Recollements of abelian and triangulated categories play an important role in geometry of singular spaces.It is a basic problem of recollement that constructing a new recollement from the known recollement(see[3-5]).

The abelianization of a triangulated category is due to the work of Verdier and Freyd, however Krause(see[6,7])gave a slightly different construction which is based on coherent functors in the sense of Auslander[8].

Abelian category and triangulated category are two fundamental structures in represent theory of algebra.The author studied the relationship between torsion theory of triangulated category D and that of its coherent functor category A(D)in[9].

In this paper,we mainly study the relationship between recollement of triangulated category D and recollement of its coherent functor category A(D).We show that the recollement of D induces the prerecollement of A(D).Furthermore,the necessary and sufficientcondition for it to be a recollement is that the recollement of D is split,i.e.,for any Y∈D, the triangles[1]induced by the adjunction morphisms satisfy h1=0 and h2=0.Because the stable categoryis a triangulated category[7],we could also get a prerecollement ofrelative toand

2　Preliminaries

Throughout the paper,we assume that k is a field and all categories are k-bilinear Hom-finite additive categories with Krull-Schmidt property,i.e.,any object can be decomposed into a direct sum of indecomposable objects,and such decomposition is unique up to isomorphisms.

First,we recall some useful definitions and results.

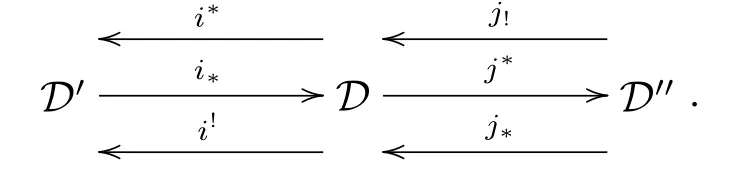
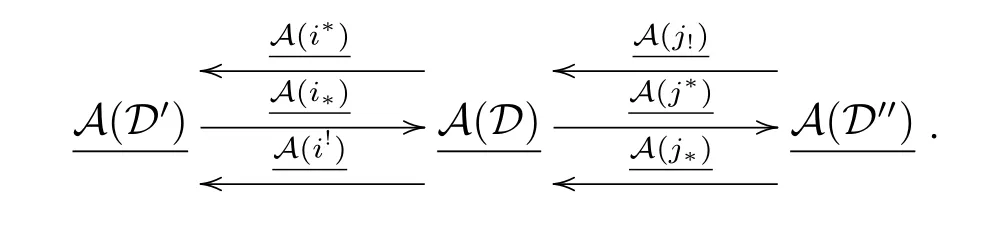
Definition 2.1[10]Let A,A＇,A＇＇be abelian categories.Then a prerecollement of A relative to A＇and A＇＇,diagrammatically expressed by

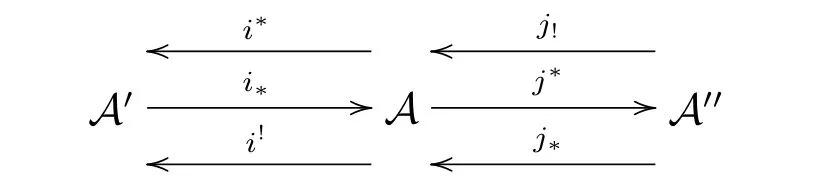
is given by six additive functors i?=i!:A＇→A;j?=j!:A→A＇＇;i?,i!:A→A＇; j?,j!:A＇＇→A,which satisfy the following three conditions:

(1)(i?,i?),(i!,i!),(j!,j!)and(j?,j?)are adjoint pairs;

(2)i?,j!and j?are full embeddings;

(3)j?i?=0.

If the prerecollement of A relative to A＇and A＇＇as above also satisfies

(4)ker(j?)=Im(i?).

Then the prerecollement is called recollement.

Remark 2.2[10]If A,A＇,A＇＇are abelian categories,and there exists a recollement as above,then

(I)i?j!=0,i!j?=0;

(II)The units and counits of adjunction give rise to exact sequences of natural transformations

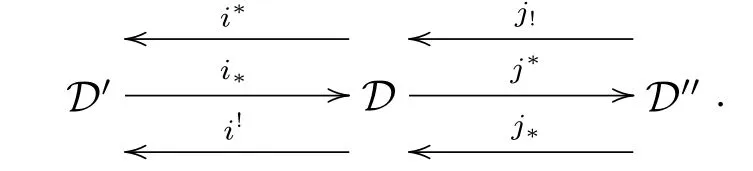
Definition 2.3 Suppose we are given triangulated categories D,D＇,D＇＇together with exact functors i?=i!:D＇→D,j?=j!:D→D＇＇,i?,i!:D→D＇,and j!,j?:D＇＇→D which satisfy the following four conditions:

(a)(i?,i?=i!,i!)and(j!,j?=j!,j?)are adjoint triples;

(b)i!j?=0(and,by adjointness,j?i?and i?j!are zero morphisms);

(c)i?,j!,j?are full embeddings(and thus i?i?i!i?idD＇and j?j!j?j?idD＇＇);

(d)any object X in D determines distinguished triangles

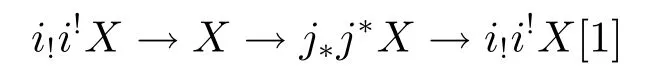
and

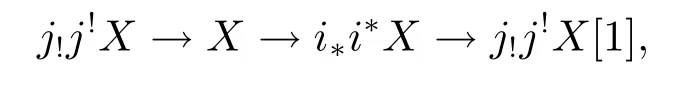
here the morphisms i!i!X→X,X→j?j?X are the adjunction morphisms.Then we say that D admits recollement relative to D＇and D＇＇,and diagrammatically expressed by

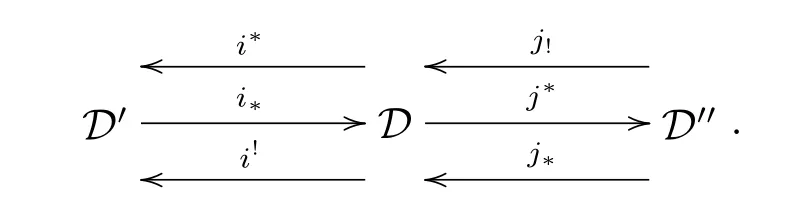
If D,D＇,D＇＇satisfy(a),(b)and(c),then we call D admits prerecollement relative to D＇and D＇＇.

Let C be an additive category.We consider functors F:Cop→Ab into the category of abelian groups and call a sequence F＇→F→F＇＇of functors exact if the induced sequence F＇X→FX→F＇＇X of abelian groups is exact for all X in C.

Definition 2.4The recollement of D in definition is called split.If for any Y∈D, the triangles(see[1])induced by the adjunction morphisms satisfy h1=0 and h2=0.

Definition 2.5[6]A functor F is said to be coherent if there exists an exact sequence (called presentation)

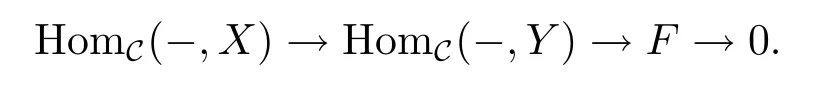
The morphisms between two coherent functors form a small set by Yoneda's lemma,and the coherent functors F:Cop→Ab form an additive category with cokernels.We denote this category by A(C).The Yoneda functor hC:C→A(C)which sends an object X to HomC(-,X)is fully faithful.

The following results are due to the work of Krause which is crucial to our construction of recollement.

Lemma 2.6[6]Let T be a triangulated category.Then

(1)the category A(T)is abelian and the Yoneda functor hT:T→A(T)is cohomological;

(2)given a cohomological functor H:T→A to an abelian category,there is(up to a unique isomorphism)a unique exact functorˉH:A(T)→A such that H=?hT;

(3)given an exact functor F:T→T＇between triangulated categories,there is(up to a unique isomorphism)a unique exact functor A(F):A(T)→A(T＇)such that hT＇?F= A(F)?hT.

Lemma 2.7[6]Let F:T→T＇and G:T＇→T be exact functors between triangulated categories.Then

(1)F is fully faithful if and only if A(F)is fully faithful;

(2)if F induces an equivalence T/ker(F)?T＇,then A(F)induces an equivalence A(T)/(kerA(F))?A(T＇);

(3)F preserves small(co)products if and only if A(F)preserves small(co)products;

(4)F is left adjoint to G if and only if A(F)is left adjoint to A(G).

Lemma 2.8[7]Let T be a triangulated category,then A(T)is a Frobenius abelian category.

3　Main Results

In this section,we assume that D,D＇,D＇＇are triangulated categories.First,we give a new proof of the following result,although it appeared already in[11].

Lemma 3.1Let D,D＇,D＇＇be three triangulated categories,and if there exists a recollement

Then the following is also a prerecollement of abelian categories:

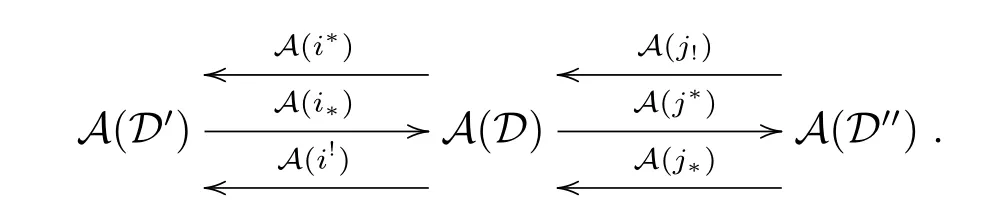
Proof From Lemma 2.7(4),(A(i?),A(i?)),(A(i!),A(i!)),(A(j!),A(j!))and(A(j?),A(j?)) are adjoint pairs.

However,there is an exact functor A(G?F):A(D)→A(D＇＇)satisfying hD＇＇?G?F= A(G?F)?hD,so we get that A(G?F)A(G)?A(F)by the uniqueness.

Then we could get that A(j?)?A(i?)A(j?i?)=0,and then condition(3)of Definition 2.1 holds.

Similarly,A(idD)idA(D).Because of the isomorphisms A(i?)A(i?)A(i??i?)idA(D)and so on,condition(2)also holds.

We prove our main results in the following.

Theorem 3.2Let D,D＇,D＇＇be three triangulated categories,and if there exists a recollement

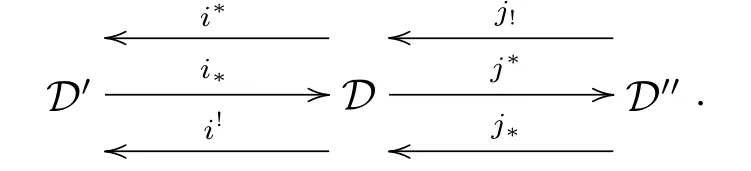
Then the prerecollement of abelian categories defined above is a recollement if and only if the given recollement of triangulated categories is split.

Proof If

is a recollement of abelian categories,then

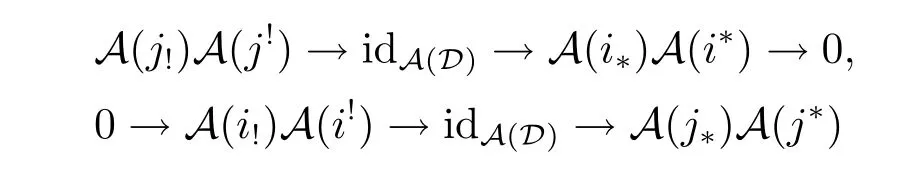
are exact.Because A(j!)A(j!)(HomD(-,Y))=HomD(-,j!j!Y)etc.hold for all HomD(-,Y)∈A(D),it is easy to see that the above two exact sequences are as follows:

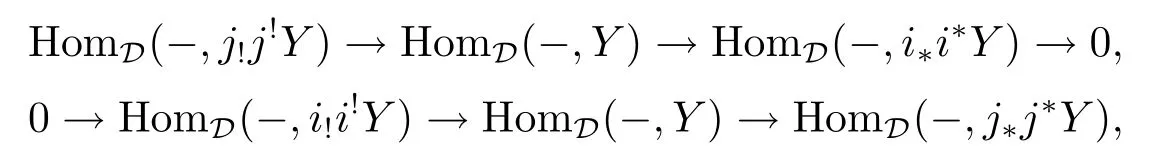
where the morphisms are also induced by the adjunction morphisms.But from

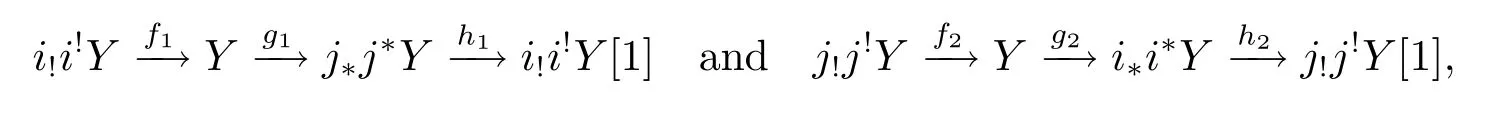
we know that HomD(-,h2)and HomD(-,h1[-1])are zero,so h1=0,h2=0.

Conversely,we only need to prove that ker(A(j?))?Im(A(i?)),since ker(A(j?))?Im(A(i?)).

Given any G∈A(D)which satisfies A(j?)G=0.First,there exists an exact sequence

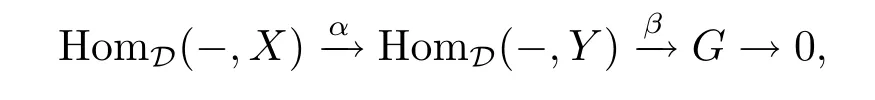
where α=HomD(-,f).So f:X→Y determines a triangleand then j?XX[1]is a triangle in D＇＇.We get that

is also exact,since A(j?)is exact and A(j?)(HomD(-,X))=HomD＇＇(-,j?X)etc..So

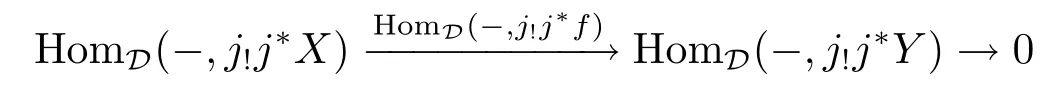
is also exact.

Because

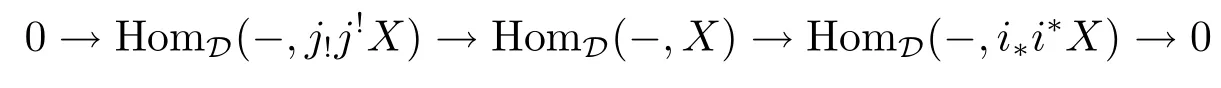
and

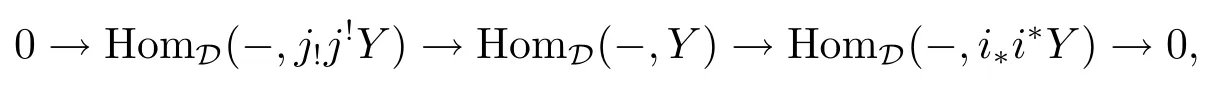
there exists the following commutative diagram:

where H is the cokernel of HomD(-,i?i?f)=A(i?)(HomD＇(-,i?f)).From“Snake lemma”, GH.H∈ImA(i?),so ker(A(j?))?Im(A(i?)).

From Lemma 2.8,A(D),A(D＇)and A(D＇＇)are all Frobenius abelian categories,so the stable categories of them are triangulated categories.We get the following corollary

Corollary 3.3Let D,D＇,D＇＇be three triangulated categories,and if there exists a recollement

Then the following is a prerecollement of triangulated categories:

Proof First,the functors in the recollement are actually triangulated functors,we only check A(i?).For any triangle inwithout generality,we assume that it is standard triangle

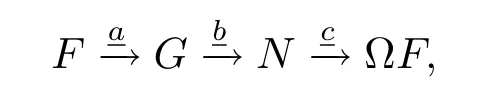
then there exists a commutative diagram in A(D):

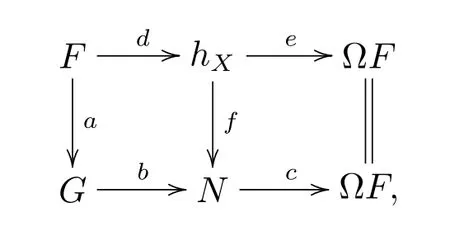
where the left square is a pushout,and the two rows are short exact sequences.A(i?)is exact in A(D),so the following is also a pushout since it is commutative and the two rows are short exact sequences.

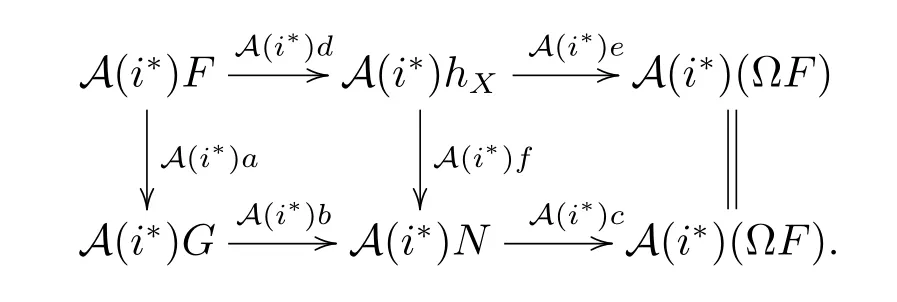
Therefore

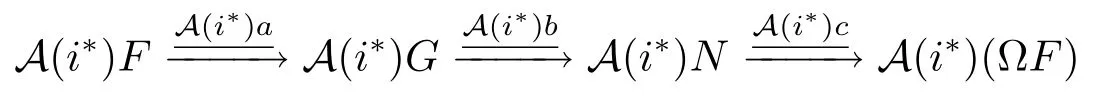
For Definition 2.3(a),we only need to prove

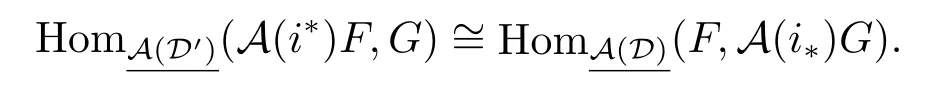
In fact,let

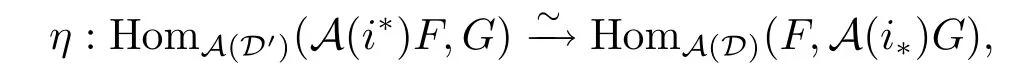
if α:A(i?)F→G factors through HomD＇(-,X＇)for some X＇∈D＇,then

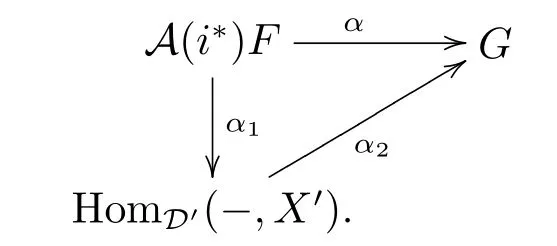
According to i?i?idD＇,there exists an object X∈D such that i?X=X＇,then

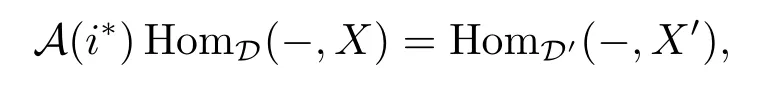
and α1=A(i?)(α＇).So

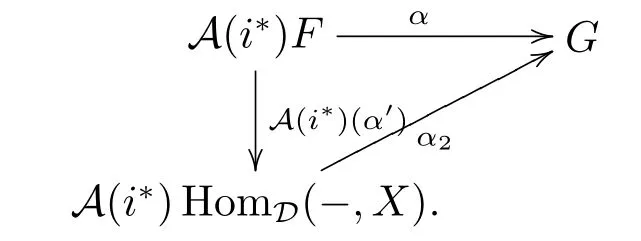
By the naturality of η,we have

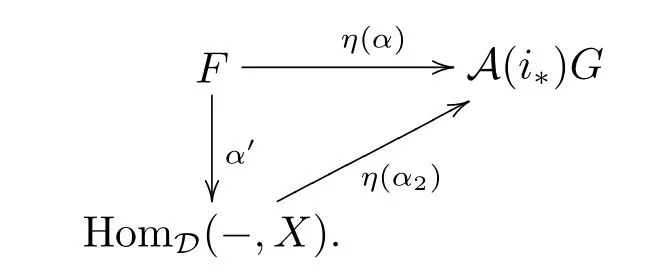
So η(α)factors through projective object.The converse is similar,so

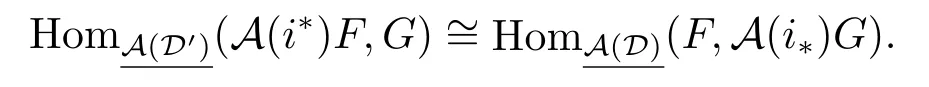
(b)is trivial.

For(c),we only need to prove thatis a full embedding,the others are similar. Since A(i?)A(i?)=idA(D＇),A(i?)is a full embeddding.It is easy to see thatis full, we only need to check that it is faithful.If HomD＇(F,G)→HomD(A(i?)F,A(i?)G)maps α to A(i?)(α)=0,then A(i?)(α)factors through some HomD(-,X),i.e.,

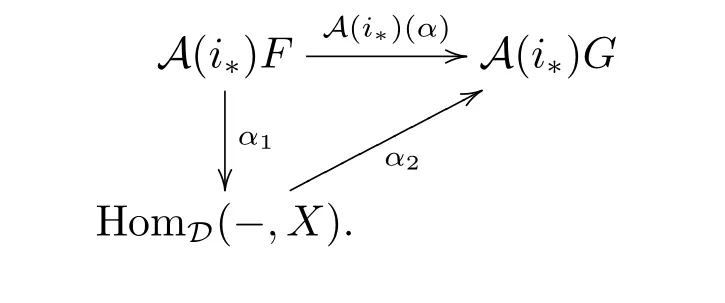
So

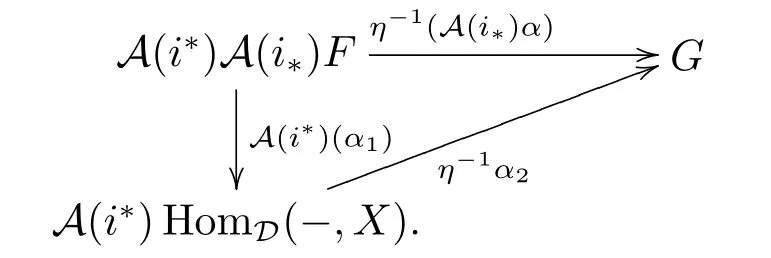
References

[1]Beilinson A,Bernstein J,Deligne P.Faisceaux pervers[J].Astrisque,1982,100:5-171.

[2]MacPherson R,Vilonen K.Elementary construction of perverse sheaves[J].Inv.Math.,1986,84(2): 403-436.

[3]Lin Zengqiang,Lin Yanan.One-point extension and recollement[J].Sci.China Ser.A,2008,51(3): 376-382.

[4]Lin Yanan,Wang Mingxiong.From recollement of triangulated categories to recollement of abelian categories[J].Sci.China Ser.A,2010,53(4):1111-1116.

[5]Han Yang.Recollements and Hochischild theory[J].J.Algebra,2014,397(1):535-547.

[6]Krause H.Localization theory for triangulated categories[A].Triangulated categories[C].Cambridge: Cambridge Univ.Press,2010:161-235.

[7]Krause H.Derived categories,resolutions,and Brown representability[A].Interactions between homotopy theory and algebra[C].Providence,RI:Amer.Math.Soc.,2007:101-139.

[8]Auslander M.Coherent functors[M].Berlin:Springer-Verlag,1966.

[9]Lin Ji.Torsion theory of triangulated categories and abelian categories[J].J.Math.,2014,34(6): 1134-1140.

[10]Franjou V,Pirashvili T.Comparison of abelian categories recollements[J].Doc.Math.,2004,9: 41-56.

[11]Wang Mingxiong.Recollements of Comma categories and category A(S)[J].J.Xiamen Univ(Nat. Sci.),2010,49(5):593-596.

[12]Hartshorne R.Coherent functors[J].Advances Math.,1998,140(1):44-94.

三角范疇的coherent函子范疇的recollement

林記

(阜陽師范學(xué)院數(shù)學(xué)與統(tǒng)計(jì)學(xué)院,安徽阜陽236037)

文章研究了三角范疇D及其coherent函子范疇A(D)的recollement之間的關(guān)系.利用D的recollement可以誘導(dǎo)A(D)的prerecollement,文章證明了該prerecollement是recollement的充分必要條件是D的recollement是可裂的;并且D的recollement可以誘導(dǎo)的prerecollement.

recollement;三角范疇;coherent函子范疇;abel范疇

MR(2010)主題分類號(hào):18E10;18E30;18E35O153.3

?date:2014-04-01Accepted date:2014-10-28

Supported by Excellent Staff Room of Fuyang Teachers College(2013JCJS03); Natural Science Foundation of Fuyang Teachers College(2015FSKJ05);Natural Science Foundation of Universities in Anhui Province(2015KJ016).

Biography:Lin Ji(1981-),female,born at Zigong,Sichuan,lecturer,major in represent theory of algebras.