Shan Gao?Xinmin Tao?Xiping Wang?Lihai Wang

Introduction

Wood is a renewable,versatile substance that is one of the world’s most fascinating materials because of its complex anisotropic structure.As an elastic material,wood can generate acoustic waves and transfer vibration when subjected to a cyclical impact force.Nondestructive acoustic methods have been used to evaluate the quality of trees,logs,lumber and wood-based composites and to detect biodeterioration of wood structural members in situ(Bucur et al.2000;Bucur 2005).The mechanical properties of wood are closely associated with acoustic wave propagation and resonance characteristics.The ultrasound wave analysis technique is based on measuring the variables in the time-of- fl ight of the acoustic waves.Various conditions are generally considered during acoustic inspection,including decay detection,defect localization and characterization and decisions to act(Gao et al.2017).An accurate understanding of the wave propagation phenomena in testing a material is the key to de fi ning the use of the analytical results needed to improve the technology.In effect,understanding wave propagation in the material is needed to successfully utilize nondestructive acoustic methods for quality assessment(Gulati et al.1981;Bucur 2006;Wang et al.2007).Researchers have reported about the relationship between acoustic wave velocity and the mechanical properties of wood since the early 1960s(James 1961;Burmester 1965).An accurate estimation of the mechanical behavior of wood requires a simultaneous view of the structure of the material and the ultrasonic wave propagation in the material,which is expressed as acoustic velocities.The mechanical properties of solid wood and wood-based composites are strongly dependent on environmental factors such as relative humidity and temperature(Gerhards 1982;Ba chle and Walker 2006;Chan et al.2010).

To fully understand the interactions between wood and its environment,we need to consider how the acoustic properties of wood are affected by temperature(e.g.,below and above freezing)and moisture content(MC)(e.g.,below or up to the fi ber saturation point).The dependence of ultrasonic velocity and related mechanical variables on the MC of wood and ambient temperature has been systematically demonstrated(Gao et al.2012,2013,2014).The relationship between the ultrasonic propagation velocity and the physical properties of wood in terms of the relationship between parallel-to-grain compressive strength and MC has also been established(Shi et al.1983).In recent years,acoustic wave technology has become more sophisticated and popular in the fi eld of wood quality assessment;however,how some environmental factors affect the acoustics of wood is still unclear.Gao et al.(2012,2013)investigated the effects of temperature and MC on the acoustic wave velocity and mechanical properties ofPinus resinosain the laboratory and in the fi eld and identi fi ed signi fi cant temperature effects on the acoustic wave velocity in frozen green wood,where the acoustic wave velocity increased as the temperature was decreased and exhibited a sudden change near 0°C.This same study showed that the rate of velocity change differed between frozen wood and non-frozen wood based on a poly-stage experimental model that quanti fi ed the relationship of temperature,MC and acoustic velocity below and above the freezing point.Based on previous successful experimental models(Gao et al.2012,2013),the objective of the present study was to theoretically model the relationship between temperature,MC and the acoustic velocity of wood to determine the effects(and related mechanisms)of temperature and MC on acoustic wave velocity(AWV)by comparing theoretical and measured values.

Materials and methods

Wood and water

At the macroscopic level,wood structure consists of main ingredients,secondary ingredients,moisture and lacuna.The cell walls of wood are considered primary ingredients,whereas secondary ingredients(wood moisture)consist of extracts,vapor and liquid water and the lacuna of wood includes tiny lacuna in the cell walls and thick lacuna such as cell cavities(Li 1994).The mass of the wood results primarily from the primary and secondary ingredients and moisture.The water in wood can be split into three categories:water that is part of the material(the removal of which would destroy the wood),free water(which resides in cell lumens or other voids)and bound water in cell walls(which forms chemical bonds to cellulose chains).Bound water is believed to be hydrogen bonded to hydroxyl groups,primarily in cellulose and hemicelluloses and to a lesser extent to the hydroxyl groups in lignin.Bound water can further be divided into surface-bound water and secondary-bound water.Surface-bound water is attracted to the tiny,active surfaces of cell walls by molecular force to form a hygroscopic water layer that is heavier than the water itself and has characteristics closer to a solid than to a liquid.Secondary-bound water is moisture that is collected in the tiny lacuna of the capillaries and is adsorbed on the hydroscopic water layer formed by the surfacebound water(Li 1994).

Phase transition of water in wood

The northeast area of China is a temperate zone,where trees undergo freezing temperatures during winter,which results in a change of state in the internal water(liquid to solid).The harm in fl icted on trees during winter has been extensively analyzed in a notable study by Tao and Jin(2005),who found that the wood body is subjected to freezing at temperatures well below the freezing point of water.

Ka renlampi et al.(2005)studied the effect of freezing duration on the liquid water content of earlywood and found that free water in the wood tissue begins to freeze when the internal temperature drops below the freezing point of water.The quantity of apparent liquid water per dry mass unit signi fi cantly differed between earlywood and latewood.Kuroda et al.(2003)used conventional scanning electron microscopy(CSEM)to observe the branch of hardwood growing in Japan and found that several ice crystals in wood ray parenchyma cells at-30°C.Roden et al.(2009)studied ice crystal formation and freezing tolerance ofPinus radiataneedles by subjecting acclimated and unacclimated needles ofP.radiatato freezing treatments.Half of the maximal electrolyte leakage occurred at-4 °C and-12 °C for unacclimated and acclimated needles respectively and ice formation occurred at similar temperatures(-3°C)in both acclimated and unacclimated pine needles.When Sparks et al.(2000)applied time domain re fl ection(TDR)technology to measure the content of liquid water in the wood tissues of ring porous wood,diffuse porous wood and coniferous species below 0 °C,they found that at 0～1 °C,more than 50% of the wood moisture was frozen and the wood intercellular aperture gradually shrank as the moisture froze.At the same time,more than 25% of the water was still in the form of a liquid in the wood tissue even at-15°C.Most likely,this liquid water was within cell walls and potentially transportable below 0°C.

In short,a review of the literature shows that free water exists in cell cavities of fi ber-saturated wood and begins to freeze when the temperature falls below the freezing point of water and that to some extent a portion of the bound water freezes at other temperatures.

Acoustic waves

Analyzing ultrasonic wave propagation in wood enables one to focus on the theoretical basis of the techniques used for measuring elastic properties(elastic modulus,tensile strength,shear yield strength).The velocity of an acoustic wave is closely associated with the physical properties of the medium through which it travels.The velocity of a longitudinal wave depends on rigidity,tensile stress and the density of a solid medium and on the compressibility and density of a liquid medium.Wave velocity through a gas medium is also affected by temperature and molecular concentration.Wave propagation status provides a wealth of useful information of various media.

If one considers frozen wood as a simple combination of wood,ice and water,the velocity of wave propagation in frozen wood is related to the individual velocities in each component.The propagation velocity of an acoustic wave is about 1403 m s-1in water(Schaafs 2006),3838 m s-1in ice at 0°C(Vogt et al.2008),and the longitudinal wave velocity in pureP.resinosawood is about 6140 m s-1at 0°C(Gao et al.2012)at standard atmospheric pressure.Table 1 shows the relationships between propagation velocity(V)of acoustic waves in each component and temperature(T)based on information obtained from previously published studies(Vogt et al.2008;Cen 2008;Gaoet al.2012).There is a strong linear relationship betweenTandVin ice,water and pure wood,with determinate coef fi cients(R2)above 0.9.The acoustic wave velocity increases continuously with decreasing temperature in ice and pure wood and increases as the temperature decreases in water.

Table 1 Relationship between T and AWV in ice,water,and American red pine wood

The acoustic wave velocity increases on average by 2.8 m s-1as temperature decreases in 1°C increments in ice and increases by about 3.73 m s-1inP.resinosapure wood when the temperature is below the freezing point of water.The acoustic wave velocity will increase by 2.75 m s-1in water for every 1°C increase and will decrease by about 1.66 m s-1in pure wood when the temperature is above 0°C.

Fundamentals

Consider the rule of mixtures for sound velocity in mixed organic liquids.Assume that the volume content of each component remains constant with changing pressure and that the acoustic propagation time in the mixture is equal to the sum of each component under ideal conditions.Based on these assumptions,Sehgal(1986)derived the equations for sound velocity in a mixture that are suitable for biological tissues and mixtures of independent,non-interacting components.The ultrasonic velocity in a liquid or a mixed liquid is determined primarily by its intermolecular properties(Jacobson 1952),and the simplest intermolecular property is the free lengthLbetween the surfaces of the molecules,in which an empirical relation exists between the two.Based on the fi ndings of Sehgal(1986)and Jacobson(1952)Yan and Zhang(2002)developed the following mixing rule of sound velocity in liquid mixture ofn-element components,where the relationship between the AWV ofn-element organic liquid mixture(c,m s-1)and the velocity in each component(ci,m s-1)is as follows:

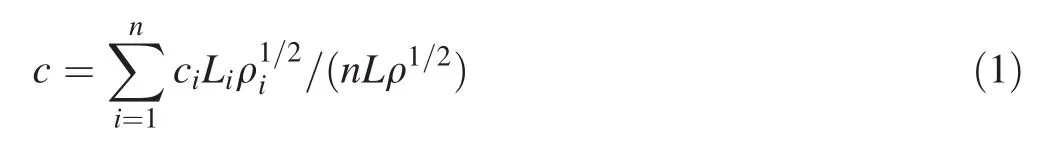
and importantly:where ρ (kg m-3)is the density of the liquid mixture,ρi(kg m-3)is the density of each liquid component,Li(m)is the free length between the surfaces of the molecules of each liquid component,andSiis the fraction of the inner surface area of each liquid component.

Acoustic wave propagating velocity in wood follows a one-dimensional wave equation:

whereV(m s-1)is the acoustic velocity in the wood,ρ(kg m-3)is the wood density,andE(MPa)is the bending elastic modulus of the wood.

Sparks et al.(2000)utilized TDR technology to examine the freezing of water in three types of wood(a coniferous species,ring porous wood,and diffuse porous wood)and found that most water in wood freezes in the temperature range of 0 to approximately-1°C,and that the liquid content of water is less than 50%below the freezing point.

Hypothesis

H1 Wood is a three-element mixture

Given that the freezing proportions of free water and bound water in wood near the freezing point and the temperature below which the water in wood is totally frozen are unknown,it was assumed that the water in wood completely froze at-τ°C(τ＞0)and that the entire temperature range could be divided into threeTzones by points–τ and 0 °C.Under these assumptions,atT＞0 °C,the moisture in the wood tissue is liquid(non-frozen wood),and the wood mixture is mainly composed of water and pure wood.At-τ°C＜T＜0°C,some of the moisture in the wood tissue is partly frozen(partly frozen wood),and the wood mixture is mainly composed of water,ice and pure wood.AtT＜-τ°C,the moisture in wood tissue is fully frozen(frozen wood),and the wood mixture is mainly composed of ice and pure wood.

H2 There are mixing rules of acoustic velocity in the wood mixture

Based on H1,it was assumed that the acoustic wave propagation velocity in the hydrated wood conformed to the mixing rules of acoustic velocity in organic liquid mixtures,so the acoustic wave velocity in wood can be expressed as follows:

whereV′is the acoustic wave velocity in wood mixture(m s-1),Viis the acoustic wave velocity in each wood component(ice,water or pure wood substance)(m s-1),fiis the volume proportion of each wood component(%),ρ is the average density of the wood mixture(kg m-3)and ρiis the density of each wood(kg m-3).

Theoretical model development

Based on the fi rst and second hypotheses,the following general theoretical model is proposed for calculating the acoustic velocity in wood:

whereV′is the acoustic wave velocity in the wood mixture(m s-1),the moisture contentu%and other parameters are represented the same as in Eq.(4).Here,Viis closely related to changes in temperature.

Then-element composition in the wood mixture has a few important features.When wood temperature is below-τ°C,the mixed components of frozen wood are ice and pure wood substance(i.e.,n=2.)When the temperature is above the freezing point(0°C),the components are water and pure wood substance(i.e.,n=2.)Finally,when the temperature ranges from –τ to 0 °C,the wood is a mixture of water,pure wood substance and ice(i.e.,n=3).

The volume proportion of ice and water in wood is dependent on temperature,MC and the ice content,all of which are not easily quanti fi ed when the temperature is very near the freezing point of water.From a practical perspective and based on previous empirical studies,it is safe to assume that acoustic testing tools should not be applied to fi eld tests on trees and logs when the temperature of the wood is near freezing.In addition,it can be assumed that the acoustic velocities of trees and logs should be adjusted for climate and season if measurements are conducted well above or below the freezing point of water(Gao et al.2013).

Accordingly,in Gao et al.(2013)study,a temperature range well above 0 °C and below-τ°C was used for the measurements.As a result,the de fi ned two-element theoretical models in Eq.(5)were tailored to both frozen wood and nonfrozen wood.For frozen wood ofu%MC(below-τ°C),was calculated as follows:

For nonfrozen woodu%MC(above 0°C),was calculated as follows:

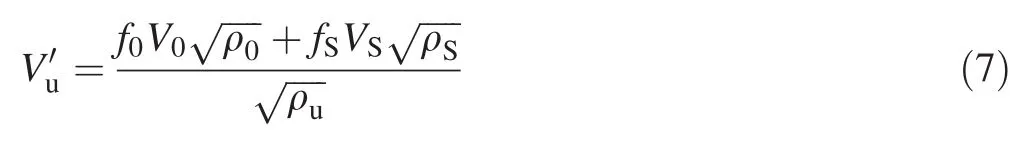
wheref0is the content of pure wood substance in the wood(%),fsis the proportion of water(%),fBis the proportion of ice(%),V0is the acoustic velocity propagation in pure wood substance(m s-1),Vsis the velocity in water(m s-1),VBis the velocity in bubble-free ice(m s-1),ρ0is the density of pure wood substance(kg m-3),ρSis the density of water(kg m-3),and ρBis the mass density of bubble-free ice(kg m-3).

MC constraints

Acoustic velocity is mainly affected by the bound water content(fbw)when MC is below the saturation point of wood fi ber(u%＜FSP).For frozen wood,fB=fbwandf0=1-fB=1-fbw.For nonfrozen wood,fS=fbwandf0=1-fS=1-fbw.Conversely,when MC is equal to or above the saturation point of the wood fi ber(u%＜FSP),then acoustic velocity is mainly affected by the free water content(ffw).Forfrozen wood,fB=ffwandf0=1-fB=1-ffw.Fornon-frozen wood,fS=ffwandf0=1-fS=1-ffw.

The combination of wood substance and bound water,which are both chemically bound,supposedly exist as a single substance rather than a mixture.Thus,the proportion of the combination is equal tof0.Thefivalue is dependent on the wood’s moisture content(u%)and can be calculated as follows:

Whenu%＜FSP,f0=1-fbwandfbw=1-1/(1+u%)×100%.

Whenu%≥FSP,f0=1-ffw,fbw=FSP/(1+u%)×100%,andffw=1-1/(1+u%)×100%-fbw.

Veri fi cation

Theoretical model veri fi cation

Fitting the theoretical model to the empirical model

According to our hypotheses and related research results(Sparks et al.2000),more than 50% of the water in wood is frozen at temperatures between-1 and 0°C.As mentioned earlier,Gao et al.(2012,2013)found that the acoustic velocity in American red pine changes dramatically near 0°C,and no second change in the velocity was observed until the temperature dropped to-40°C.The rate of acoustic velocity remained constant as the temperature decreased below the freezing point of water.

According to the established fact that the FSP of American red pine is 24%,the parameter τ in the developed theoretical model was set to equal 2.5 for empirical veri fi cation.The values of the acoustic velocity of wood in the temperature range of-40 to-2.5°C were calculated according to Eqs.6 and 7.The changes are shown in Figs.1 and 2.

The results in Fig.1 are a product of the respective measurements of acoustic velocity that correspond to the temperature-40,-30,-20,-10,and-5°C with a set wood MC(from 0.2 to 118.3%MC).The data in Fig.2 are the calculated acoustic velocities measured at temperatures 0,5,10,20,and 30°C.In both fi gures,the round solid data points represent the experimentally measured values of acoustic velocity at the corresponding temperatures and MCs obtained from the literature(Gao et al.2012),whereas the square hollow data points represent the predicted values of acoustic velocity,which were calculated using Eqs.(6)and(7).

Figure 1 shows that the predicted values below 0°C had little deviation and were quite close to the measured values,especially below the fi ber saturation point(MC＜24.8%).This observation demonstrates that the developed theoretical model fi t the empirical model well.The difference between the theoretically predicted values and the measured values was relatively large at temperatures above the freezing point of water and particularly above the fi ber saturation point(MC＞24.8%;Fig.2),which suggests that the theoretical model is very applicable above 0°C.

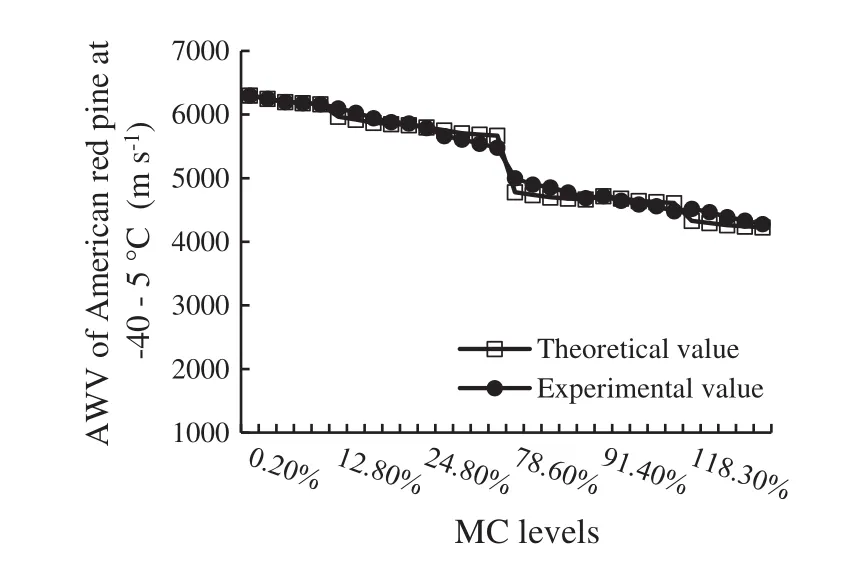
Fig.1 Comparison between theoretically predicted and measured acoustic velocities at-40–5 °C at various MC levels

Fig.2 Comparison between theoretically predicted and measured acoustic velocities at 0–30 °C at various MC levels

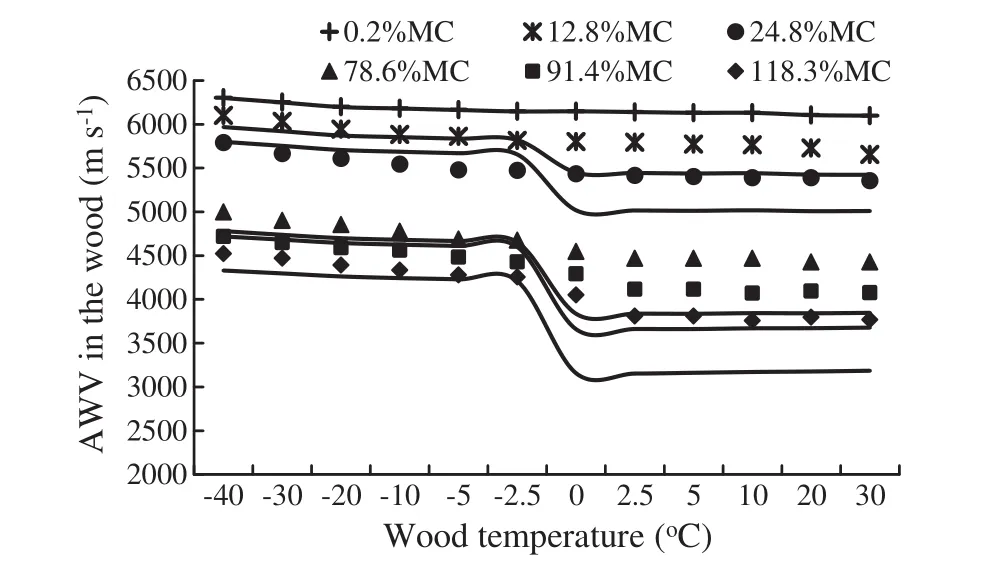
Fig.3 Relationship between predicted acoustic velocity of wood and temperature at various MC levels with the theoretical and experimental models

Figure 3 illustrates the relationships between temperature,measured values and the predicted values of the acoustic velocity in wood with different MCs.The data points represent the calculated values of acoustic velocity as determined using the experimental model of Gao et al.(2012),and the solid lines represent the change in the predicted acoustic velocity with temperature based on the theoretical model.Temperature breakpoints were selected based on previous experimental observations of the velocity–temperature effects between 2.5 and 0 °C,which showed a distinct difference from the effect below-2.5°C or above 0°C.The velocity of green wood changed at around 0°C.It was noticed that there was a dramatic shift in acoustic velocity in the freezing zone,which produced discontinuities at the breaking points in the segmented theoretical models,but no apparent velocity discontinuity was observed in the dry wood samples.Gao et al.(2012,2013)attributed the dramatic shift in velocity around the freezing point to the phase transformation of free water in the wood cells.The entire change of velocity in relation to temperature agreed well with the theory and with the experimental results.

It appeared that the theoretically predicted values(Figs.1,2,3)were generally lower than the experimental measured values,which most likely was due to overestimation of the effects of MC on the velocity-temperature relationship in the theoretical model(Eq.7).The acoustic wave velocity ranged from 6198 to 6098 m s-1in the pure wood substance(dry wood)(Gao et al.2012)when the temperature was above 0°C and ranged from 1403 to 1507 m s-1in liquid water(Schaafs 2006;Vogt et al.2008).The effect of moisture on the acoustic velocity in wood became increasingly signi fi cant as the wood MC increased(Eq.7),especially in green frozen wood.

We speculated that there were two main reasons that the theoretically predicted values in frozen wood fi t the empirical values better than the theoretically predicted values of the non-frozen wood.These reasons are discussed next.

(1)Constraint limitation of the theoretical model

When the temperature is below the freezing point of water,the wood is regarded as a mixture of solid materials(ice and pure wood substance)(Li 1994).Most of the water vapor and free water in the cell cavities and intercellular space is frozen,and the liquid water formed ice crystals.The non-frozen,bound water was chemically attached to the wood substance body by hydrogen bonds,which regularly arranged water molecules and distributed them on the inner surface of the cell walls to form a compact molecular layer of hygroscopic water.The nature of this molecular layer is closer to that of a solid material than a liquid,because its mass is greater than water despite its liquid form.As a result,the theoretical model(Eq.6)exhibited a better fi t following the assumption that the wood was composed of solid ice and solid wood substances,which conforms to the constraints imposed by the acoustic velocity mixing rules(H2).When the temperature was above the freezing point,the wood was a mixture of solid and liquid components,which failed to comply with acoustic velocity mixing rules and resulted in a less accurate prediction of behavior(Eq.7).

(2)Inaccurate description of constraints,the location of the impact factor

The results of this study have shown that the effect of the MC on the acoustic velocity in non-frozen wood is not remarkable when the water content is higher than the fi ber saturation point.However,the MC of wood in the Eq.7 is one of the main factors that led to the overestimation of the acoustic velocity in wood,thereby obfuscating the accuracy of the model’s predictions.

Validity of the theoretical model for frozen wood

Table 2 shows the predictionerror(%)between the theoretically predicted values()and experimentally measured values(Vu)of the acousticvelocity in wood with an MC ofu%:η=100× |Vu-|/Vu.The maximum error in the prediction for frozen wood was 4.24%,the minimum error was 0.02%,and the average error was 1.66%.In the case of the non-frozen wood,the maximum prediction error was 22%,the minimum was 4.1%,and the average error was 9.1%.Figure 4 shows the total correlation between the predicted values and measured values of acoustic velocity in frozen wood.The determinate coef fi cientR2was 0.981.

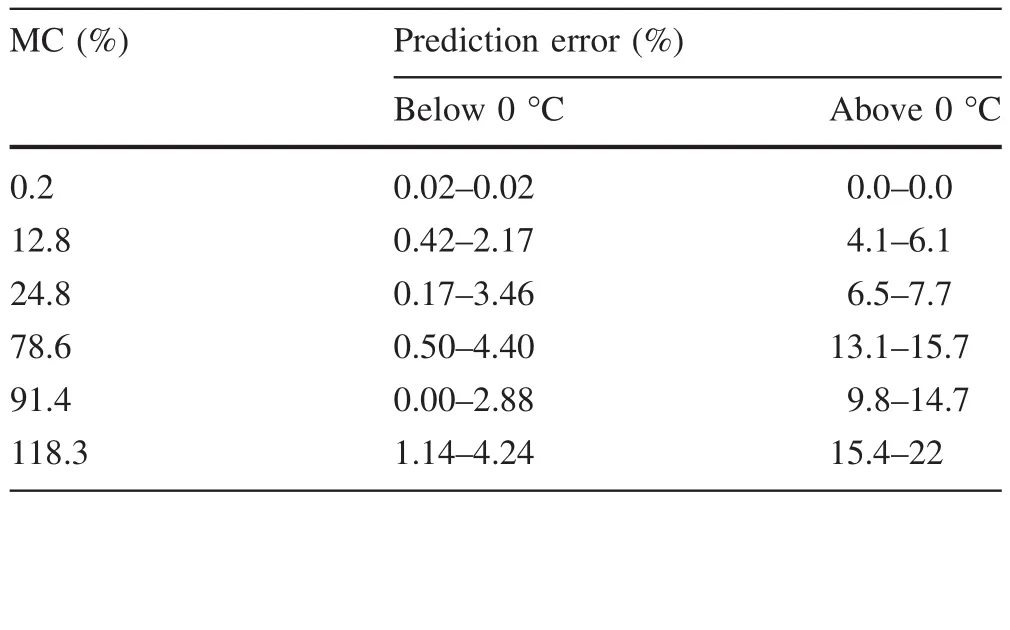
Table 2 Prediction error of theoretical model at-40–5 °C

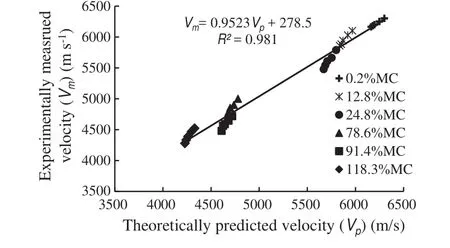
Fig.4 Relationship between predicted and measured values of acoustic velocity in wood below freezing point of water

Conclusion

To investigate the effects and related mechanisms of temperature(particularly low temperature)and MC on the acoustic velocity in wood,a general theoretical model was constructed that de fi ned the relationship between these factors.This model was predicated on the hypothesis that wood is a mixture,and its nature is temperature dependent.According to the velocity differences in the main components of the wood mixture(ice,water,and pure wood substance),the validity of the model was discussed as it was separately applied to frozen and non-frozen wood.By comparative analysis between the theoretical model and experimental models,as applied to American red pine(P.resinosa).

The predicted AWV at various moisture levels fi t the experimental results very well when the temperature of the wood was below 0°C,with an average prediction error of 1.66%.The theoretically predicted AWV experienced a sudden change near 0°C and increased rapidly in green wood as temperature decreased,which was consistent with the experimental observations.The prediction error of the model was relatively large,however,which was attributed to an overestimation of the effects of liquid water content in wood on the acoustic velocity.

The high correlation between the predicted and measured values in frozen wood theoretically revealed the mechanism by which temperature affected acoustic velocity,further verifying the reliability of the previous experimental model with regard to the effects of temperature on the acoustic velocity in wood.

Ba chle H,Walker J(2006)The in fl uence of temperature on the velocity of sound in green pine wood.Holz Roh Werkst 64:429–430

Bucur V(2005)Ultrasonic techniques for nondestructive testing of standing trees.Ultrasonics 43(4):237–239

Bucur V(2006)Acoustic of wood.In Proceedings:the thirteenth international congress on sound and vibration(ICSV13),July 2–6,2006,Vienna,pp 1–16

Bucur V,Barlow CY,Garros S(2000)The effect of hydrostatic pressure on physical properties and microstructure of spruce and cherry.Holzforschung 54:83–92

Burmester VA(1965)Zusammenhang of Zwischen Schallgeschwindigkeit und Morphologischen,Physikalischen und Mechanischen Eigenschaften Von Holz.Holz Als Roh-und Werkstoff 23(6):227

Cen M(2008)Relationship between ultrasonic velocity in liquid and temperature.Phys Exp 28(5):39–41(In Chinese)

Chan JM,Walker JC,Raymond CA(2010)Effects of moisture content and temperature on acoustic velocity and dynamic MOE of radiata pine sapwood boards.Wood Sci Technol 45:609–626

Gao S,Wang X,Wang L,Allison RB(2012)Effect of temperature on acoustic evaluation of standing trees and logs:part 1—Laboratory investigation.Wood Fiber Sci 44(3):286–297

Gao S,Wang X,Wang L,Allison RB(2013)Effect of temperature on acoustic evaluation of standing trees and logs:part 2—Field investigation.Wood Fiber Sci 45(1):15–25

Gao S,Wang N,Wang L,Han J(2014)Application of an ultrasonic wave propagation fi eld in the quantitative identi fi cation of cavity defect of log disc.Comput Electron Agric 108:23–129

Gao S,Wang X,Wiemann MC et al(2017)A critical analysis of methods for rapid and nondestructive determination of wood density in standing trees.Ann For Sci 74:27–39

Gerhards CC(1982)Effect of moisture content and temperature on the mechanical properties of wood:an analysis of immediate effects.Wood Fiber Sci 14(1):24–36

Gulati AS,Jain JD,Sanyul SN(1981)Effect of different variables on the propagation of ultrasonic waves in timber.J Timber Dev Assoc 27(2):17–19

Jacobson B(1952)Ultrasonic velocity in liquids and mixtures.J Chem Phys 20:927

James WL(1961)Effect of temperature and moisture content on internal friction and speed of sound in Douglas- fi r.For Produc J 11(9):383–390

Ka renlampi PP,Tynja la P,Stro m P(2005)Phase transformations of wood cell wall water.J Wood Sci 51:118–123

Kuroda K,Kasuga J,Arakawa K,Fujikawa S(2003)Xylem ray parenchyma cells in boreal hardwood species respond to subfreezing temperatures by deep super cooling that is accompanied by incomplete desiccation.Plant Physiol 131:736–744

Li J(1994)Wood science.Press of Northeast Forestry University,Harbin(In Chinese)

Roden JS,Canny MJ,Huang CX,Ball MC(2009)Frost tolerance and ice formation inPinus radiataneedles:ice management by the endodermis and transfusion tissues. Funct Plant Biol 36(2):180–189

Schaafs W(2006)The sound velocity in water,H2O and D2O molecular acoustics Landolt–Bo rnstein,new series,group II molecules and radicals V.Springer,Berlin,pp 69–72

Sehgal CM(1986)Measurement and use of acoustic nonlin-earity and sound speed to estimate composition of excislivers.Ultrasound Med Boil 12(1):865–874

Shi B,Yin S,Ruan X(1983)Wood sound velocity researchI Relationship between physical parameters of sound velocity,compression strength parallel to the grain and moisture content.J Nanjing For Univ 7(3):6–12(In Chinese)

Sparks JP,Campbell GS,Black RA(2000)Liquid water content of wood tissue at temperatures below 0°C.Can J For Res 30:624–630

Tao D,Jin Y(2005)The harm that trees experience in winter.Press of Science,Beijing(In Chinese)

Vogt C,Laihem K,Wiebush C(2008)Speed of sound in bubble-free ice.J Acoust Soc Am 124(6):1–6

Wang X,Carter P,Ross RJ,Brashaw BK(2007)Acoustic assessment of wood quality of raw forest materials—a path to increased pro fi tability.For Prod J 56:6–14

Yan X,Zhang Y(2002)Study on mixing rule of sound velocity in Organic liquid mixture.J Univ Pet 26(1):112–114(In Chinese)