黃兆麟

(天津水運(yùn)高級(jí)技工學(xué)校 300456)

在△ABC中,設(shè)∠A,∠B,∠C的對(duì)邊分別為a,b,c,則有

(1′)

(2′)

(3′)

本刊文[1]給出了以上三個(gè)三角形不等式不同風(fēng)格的證明,但不宜指數(shù)推廣,本文則給出這三個(gè)不等式指數(shù)推廣的證明,方法異于文[1].首先將不等式(1′)及(2′)統(tǒng)一推廣為：

定理1在△ABC中,設(shè)∠A,∠B,∠C的對(duì)邊分別為a,b,c,則當(dāng)指數(shù)k≥1,有

≥akcosA+bkcosB+ckcosC

(Ⅰ)

證明首先分兩部分證明不等式鏈(Ⅰ)中第一個(gè)不等式.

①當(dāng)k=1時(shí),不等式鏈(Ⅰ)中第一個(gè)不等式即為不等式(2′),而由正弦定理知不等式(2′)又可等價(jià)為如下不等式(1),

(1)

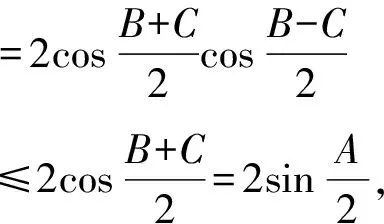
設(shè)此時(shí)不等式(1)左右之差為M1,則

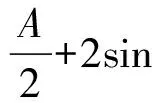
-sin (B+C)-sin (C+A)-sin (A+B)

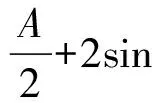
-(sinBcosC+cosBsinC)-(sinCcosA

+cosCsinA)-(sinAcosB+cosAsinB)

顯然以上最后一式的三個(gè)單項(xiàng)均為非負(fù)項(xiàng),故有2M1≥0,即不等式(1)成立,

從而不等式(2′)成立,也就是當(dāng)k=1時(shí)不等式鏈(Ⅰ)中第一個(gè)不等式成立.

②當(dāng)k>1時(shí),由不等式鏈(Ⅰ)中第一個(gè)不等式的完全對(duì)稱性,不妨設(shè)A≥B≥C,則有

又記此時(shí)不等式鏈(Ⅰ)中第一個(gè)不等式左右之差為M,那么

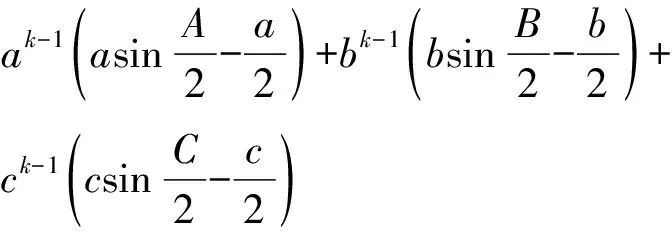
即當(dāng)k>1時(shí)不等式鏈(Ⅰ)中第一個(gè)不等式也成立.

以上證明最后一步用到了不等式(2′)成立的結(jié)論.

綜上①與②知當(dāng)k≥1時(shí)不等式鏈(Ⅰ)中第一個(gè)不等式成立.

由以上證明過程可看出,不等式(2′)強(qiáng)于不等式(1′).

下面再證明不等式鏈(Ⅰ)中第二個(gè)不等式：

由不等式鏈(Ⅰ)中第二個(gè)不等式的完全對(duì)稱性,不妨設(shè)A≥B≥C,則有

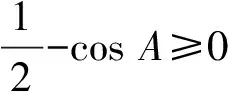
又記此時(shí)不等式鏈(Ⅰ)中第二個(gè)不等式左右之差為M2,那么

即當(dāng)指數(shù)k≥1時(shí)不等式鏈(Ⅰ)中第二個(gè)不等式也成立.

以上證明最后一步用到了熟知的不等式

至此定理1全部獲證.

順便指出,由以上證明過程不難看出,對(duì)于不等式鏈(Ⅰ)中的第二個(gè)不等式,指數(shù)可放寬為正數(shù).

下面再將不等式(3′)指數(shù)推廣為：

定理2在△ABC中,設(shè)∠A,∠B,∠C的對(duì)邊分別為a,b,c,且指數(shù)k為正數(shù),則有

(Ⅱ)

證明首先給出不等式鏈(Ⅱ)中第一個(gè)不等式一種直接證法(下文還有一種間接證法).

由不等式鏈(Ⅱ)中第一個(gè)不等式的完全對(duì)稱性,不妨設(shè)A≥B≥C,則有

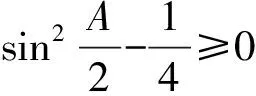
又記此時(shí)不等式鏈(Ⅱ)中第一個(gè)不等式左右之差為M,那么

即不等式鏈(Ⅱ)中第一個(gè)不等式成立.

以上最后一步用到了熟知的不等式

下面再證明不等式鏈(Ⅱ)中第二個(gè)不等式：

將不等式鏈(Ⅱ)中第一個(gè)不等式里的正弦函數(shù),利用平方關(guān)系置換為余弦函數(shù)即得

即不等式鏈(Ⅱ)中第二個(gè)不等式也成立.

至此定理2全部獲證.

接下來再給出定理1的一個(gè)類似.

定理3在△ABC中,設(shè)∠A,∠B,∠C的對(duì)邊分別為a,b,c,則當(dāng)指數(shù)k≥1,有

(Ⅲ)

證明首先分兩部分證明不等式鏈(Ⅲ)中的第一個(gè)不等式

①當(dāng)k=1時(shí),設(shè)此時(shí)鏈(Ⅲ)中第一個(gè)不等式左右之差為M11,利用余弦定理可得

+ca+ab)

即當(dāng)k=1時(shí)鏈(Ⅲ)中第一個(gè)不等式成立.

②當(dāng)k>1時(shí),由不等式鏈(Ⅲ)中第一個(gè)不等式的完全對(duì)稱性,不妨設(shè)A≥B≥C,則有

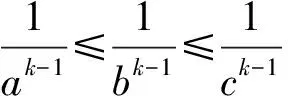
又記此時(shí)不等式鏈(Ⅲ)中第一個(gè)不等式左右之差為M12,那么

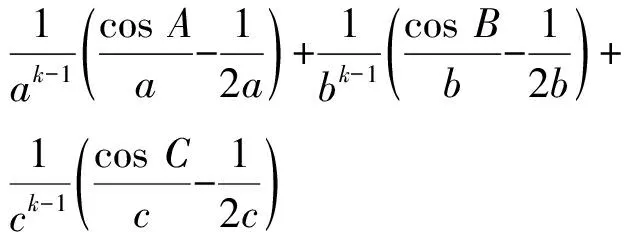
即當(dāng)k>1時(shí)不等式鏈(Ⅲ)中第一個(gè)不等式也成立.

以上證明最后一步用到了k=1時(shí)鏈(Ⅲ)中第一個(gè)不等式成立的結(jié)論.

綜上①與②知當(dāng)k≥1時(shí)不等式鏈(Ⅲ)中第一個(gè)不等式成立.

下面再證明不等式鏈(Ⅲ)中第二個(gè)不等式：

由不等式鏈(Ⅲ)中第二個(gè)不等式的完全對(duì)稱性,不妨設(shè)A≥B≥C,則有

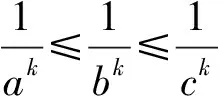
又記此時(shí)不等式鏈(Ⅲ)中第二個(gè)不等式左右之差為M2,那么

即不等式鏈(Ⅲ)中第二個(gè)不等式也成立.

以上證明最后一步用到了熟知的不等式

至此定理3全部獲證.

順便指出,由以上證明過程不難看出,對(duì)于不等式鏈(Ⅲ)中的第二個(gè)不等式,指數(shù)可放寬為正數(shù).

下面再給出定理3的一個(gè)類似.

定理4在△ABC中,設(shè)∠A,∠B,∠C的對(duì)邊分別為a,b,c,且指數(shù)k為正數(shù),則有

(Ⅳ)

證明先證明鏈(Ⅳ)中第一個(gè)不等式.

以下證明需分類討論：

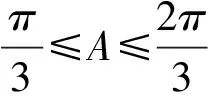
又設(shè)鏈(Ⅳ)中第一個(gè)不等式左右之差為M1,那么

即此時(shí)鏈(Ⅳ)中第一個(gè)不等式成立.

以上證明最后一步用到了熟知的不等式

即此時(shí)鏈(Ⅳ)中第一個(gè)不等式也成立.

綜①和②知鏈(Ⅳ)中第一個(gè)不等式成立.

再證明鏈(Ⅳ)中第二個(gè)不等式也成立：

將不等式鏈(Ⅳ)中第一個(gè)不等式里的余弦函數(shù),利用平方關(guān)系置換為正弦函數(shù)即得

移項(xiàng)整理即得

即不等式鏈(Ⅳ)中第二個(gè)不等式也成立.

至此定理4全部獲證.