陜西省漢中市鎮(zhèn)巴中學(723600) 劉再平 李 靖

對于實數a,b,且a?=b,定義為a,b的指數平均數,則.

證明先證指數平均不等式的右邊,如下：

不妨設a＞b,即a-b＞0,ea-eb＞0,要證不等式的右邊,即證a-b＞,則證換元,令a-b=t＞0,所以需證構造函數即證f(x)＞0.求導得即f(x)為(0,+∞)上的增函數,則f(x)＞f(0)=0,不等式右邊得證,同理可證不等式左邊.

綜上述所,指數平均不等式鏈得證.

上述指數平均不等式有著優(yōu)美的幾何意義,即“無字證明”,如下：

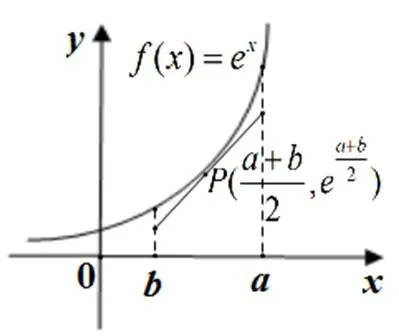
圖1

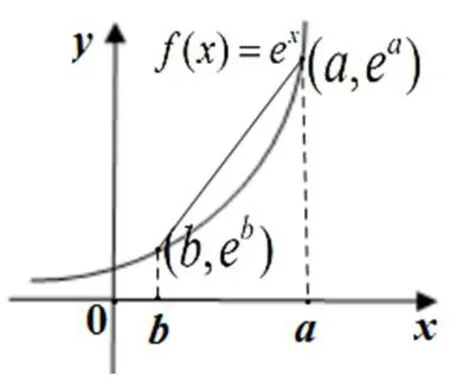
圖2

如圖1,曲邊梯形面積大于直角邊梯形面積,即S曲梯＞S直梯,所以,即ea-eb＞則故不等式左邊得證;

如圖2,直角邊梯形面積大于曲邊梯形面積,即S曲梯＜S直梯,所以,即ea-eb＜,則,故不等式右邊得證.

綜上述所,指數平均不等式鏈得證.

運用上述指數平均不等式可以簡解下述函數與導數壓軸題.

例1已知函數f(x)=ex,x1,x2∈R,且x1?=x2,若求k的取值范圍.

解由題不妨設x1＞x2,即x1-x2＞0,所以由指數平均不等式|k|(ex1+ex2),又ex1+ex2＞0,所以,即或.

點評此題運用指數平均不等式的右邊恰到好處的放縮了原不等式,快速的獲得了關于參數k的不等關系,簡潔的求得了k的取值范圍.

例2(2013年高考陜西理科壓軸題)已知函數f(x)=ex,x∈R.

(Ⅰ)若直線y=kx+1與f(x)的反函數的圖像相切,求實數k的值;

(ⅠⅠ)設x＞0,討論曲線y=f(x)與曲線y=mx2(m＞0)公共點的個數.

(ⅠⅠⅠ)設a＜b,比較的大小,并說明理由.

解(Ⅰ)k=;

(ⅠⅠ)當 0＜m＜時,無公共點;當時,有1個公共點;當m＞時,有2個公共點.

點評此道壓軸題的壓軸問只需要將題意翻譯之后,便是指數平均值不等式的右邊,問題迅速解決.

學習數學就要善于解題,數學解題的工具是雙基,正如波利亞所說：“貨源充足和組織良好的知識倉庫是一個解題者的重要資本”,也就是說知識面越廣對數學解題的幫助勢必越大,而此文闡述的指數平均不等式雖然教材上未曾提及,然而無疑是解決相關高考壓軸題的好工具.