LOCAL CONVERGENCE OF INEXACT NEWTON-LIKE METHOD UNDER WEAK LIPSCHITZ CONDITIONS?
Ioannis K.ARGYROS
Department of Mathematical Sciences,Cameron University,Lawton,OK 73505,USA
E-mail:iargyros@cameron.edu
Yeol Je CHO?
School of Mathematical Sciences,University of Electronic Science and Technology of China,Chengdu 611731,China
Department of Mathematics Education,Gyeongsang National University,Jinju 52828,Korea
E-mail:yjcho@gnu.ac.kr
Santhosh GEORGE
Department of Mathematical and Computational Sciences,National Institute of Technology Karnataka,757 025 India
E-mail:sgeorge@nitk.ac.in
Yibin XIAO(肖義彬)
School of Mathematical Sciences,University of Electronic Science and Technology of China,Chengdu 611731,China
E-mail:xiaoyb9999@hotmail.com
Abstract The paper develops the local convergence of Inexact Newton-Like Method(INLM)for approximating solutions of nonlinear equations in Banach space setting.We employ weak Lipschitz and center-weak Lipschitz conditions to perform the error analysis.The obtained results compare favorably with earlier ones such as[7,13,14,18,19].A numerical example is also provided.
Key words inexact Newton method;Banach space;semilocal convergence;weak and center-weak Lipschitz condition;recurrent functions;Kantorovich hypotheses
1 Introduction
Let X,Y be Banach spaces and D be a non-empty convex and open subset in X.Let U(x,r)and(x,r)stand,respectively,for the open and closed ball in X with center x and radius r>0.Denote by L(X,Y)the space of bounded linear operators from X into Y.In this paper,we are concerned with the problem of approximating a solution x?of equation

where F is a Fr′echet continuously differentiable operator de fined on D with values in Y.
Using mathematical modelling,many problems from computational sciences and other disciplines can be brought in the form of equation(1.1)(see,for example,[3,5,9,10,12,18]),which is related to many problems such as inclusion problems and variational inequalities etc(see,for example,[16,17,20]).The solution of these equations can rarely be found in closed form.That is why the solution methods for these equations are iterative.In particular,the practice of numerical analysis for finding such solutions is essentially connected to variants of Newton’s method[1–15,18,19].The study about convergence matter of iterative procedures is usually centered on two types:semilocal and local convergence analysis.The semilocal convergence matter is,based on the information around an initial point,to give criteria ensuring the convergence of iterative procedure,while the local one is,based on the information around a solution,to find estimates of the radii of convergence balls.There is a plethora of studies on the weakness and/or extension of the hypothesis made on the underlying operators(see,for example,[1–15,18,19]).
Undoubtedly,the most popular iterative method,for generating a sequence approximating x?,is Newton’s method(NM)which is de fined as
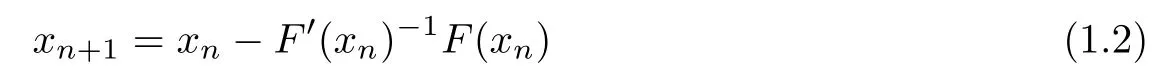
for each n≥0,where x0is an initial point.There are two difficulties with the implementation of the method(NM).The first is to evaluate F′and the second difficulty is to exactly solve the following Newton equation
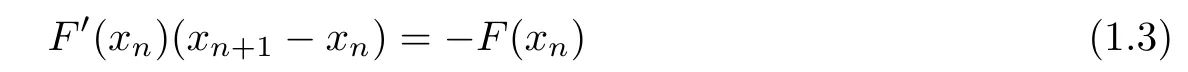
for each n≥0.It is well-known that evaluating F′and solving equation(1.3)may be computationally expensive[3,7,9,11,18,19].That is why the inexact Newton method(INLM)has been used[3,4,11,12,18,19].
For n=0,the step 1 until the convergence do.
Find the step?nwhich satis fies
where
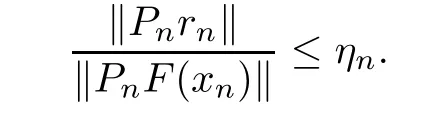
Set xn+1=xn+?n,where Pnis an invertible operator for each n≥0.Here{rn}is a null-sequence in the Banach space Y.Clearly,the convergence behavior of the method(INLM)depends on the residual controls of{rn}and the hypotheses on F′.In particular,the Lipschitz continuity conditions on F′have been used and residual controls of the form
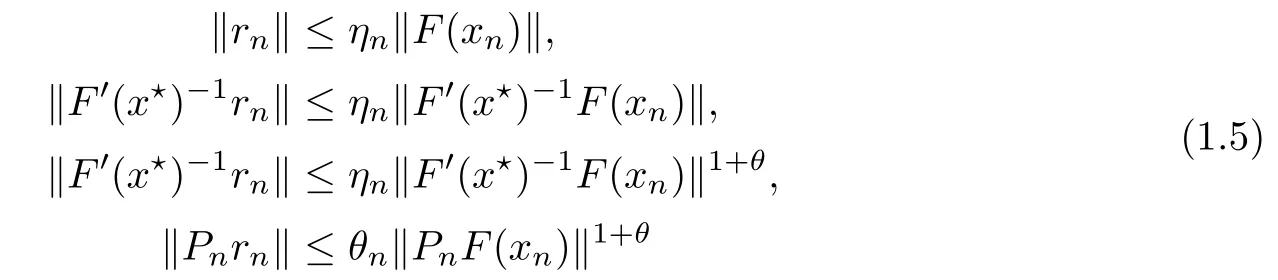
for some θ∈ [0,1]and for each n ≥ 0 have been employed.Here{ηn},{θn}are the sequences in[0,1],{Pn}is a sequence in L(Y,X)and F′(x?)?1F′satis fies the Lipschitz condition or the H?lder condition on U(x?,r)(see[3–9,11–13,19]).
In this paper,we are motivated by the works of Argyros et al.[3,4],Chen et al.[7]and optimization considerations.We suppose that F has a continuous Fr′echet-derivative in(x?,r),F(x?)=0,F′(x?)?1F′exists and F′(x?)?1F′satis fies the Lipschitz with the L-average radius condition
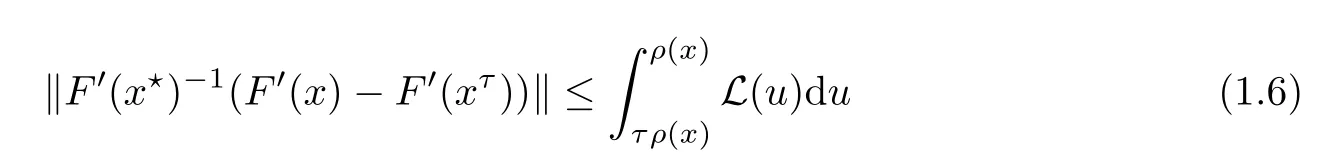
for each x ∈ U(x?,r).Here,τ∈ [0,1]and L is a monotone function on[0,r].Condition(1.6)was inaugurated by Wang[19].
In view of(1.6),there exists a monotone function L0on[0,r]such that the center Lipschitz with L0-average condition
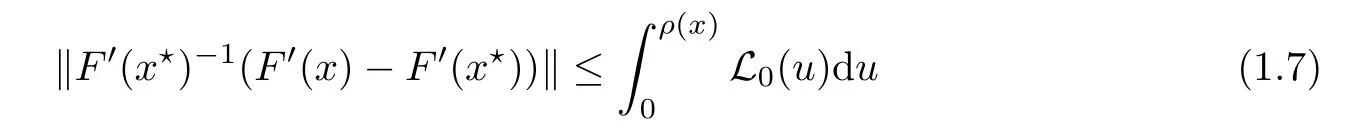
holds for each x ∈ U(x?,r).Clearly,we have

for each u∈[0,r]and L/L0can be arbitrarily large[3,4,6](see also the numerical example at the end of the study).It is worth noticing that(1.7)is not an additional to(1.6)hypothesis since in practice the convergence of(1.6)requires the computation of(1.7).
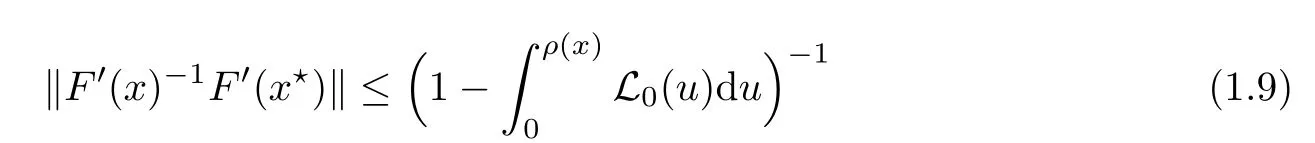
for each x ∈ U(x?,r)instead of using(1.6)to obtain
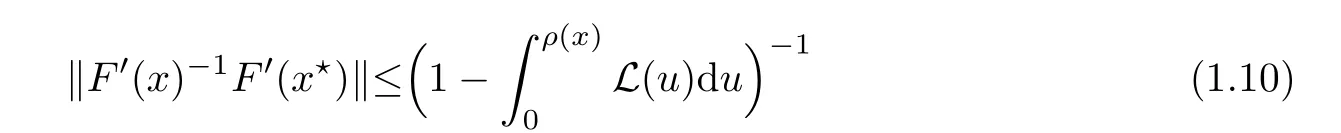
for each x ∈ U(x?,r).
Notice that(1.6)and(1.10)were used in[7,19].It turns out that using(1.9)instead of(1.10),in the case when L0(u) 1)Larger radius of convergence. 2)Tighter error estimates on the distancesfor each n ≥ 0. 3)Fewer iterations to achieve a desired error tolerance. The rest of the paper is organized as follows:In Section 2,we present some auxiliary results.Section 3 contains the local convergence analysis of the method(INLM).In Section 4,we present special cases.Finally,the numerical example appears in Section 5 and the conclusion in Section 6. In this section,we present three auxiliary results.The first two are Banach-type perturbation lemmas. Lemma 2.1Suppose that F is such that F′is continuously Fr′echet-differentiable in U(x?,r),F′(x?)?1∈ L(Y,X)and F′(x?)?1F′satis fies the center-Lipschitz condition with L0-average.Let r satisfy Then,for each x ∈ U(x?,r),F′(x)is invertible and Thus it follows from(2.3)and the Banach lemma on invertible operators[10]that F′(x)?1∈L(Y,X)and(2.2)holds.This completes the proof. Lemma 2.2Suppose that F is such that F′is continuously Fr′echet-differentiable in U(x?,r),F′(x?)?1∈ L(Y,X)and F′(x?)?1F′satis fies the radius Lipschitz condition with L-average and the center-Lipschitz condition with L0-average.Then we have ProofLet x ∈ U(x?,r).Using(1.7)and(2.1),it follows in turn that If F′(x?)?1F′satis fies the center-Lipschitz condition,then we have ProofLet x ∈ U(x?,r).We have But,in view of(2.2)and the estimate shown in[7,Lemma 2.1,1.3],we obtain which implies(2.4)and,since L0(u)≤L(u),(2.4)implies(2.5).Estimate(2.6)is shown in[7,Lemmas 1.3,2.2]. Remark 2.3If L0=L,then our two preceeding results are reduced to the corresponding ones in[7].Otherwise,i.e.,if the strict inequality holds in(1.8),then our estimates are more precise since and Notice that the right hand sides of(2.9)and(2.10)are the upper bounds of the norms,respectively obtained in the corresponding lemmas in[7].It turns out that in view of estimates(2.9)and(2.10),we obtain the advantages already mentioned in Introduction of this paper of our approach over the corresponding ones in[7,19]. Next,we present another auxiliary result due to Wang[19,Lemma 2.2]. Lemma 2.4Suppose that the function Lαde fined by is nondecreasing for some α with α ∈ [0,1],where L is a positive integrable function.Then,for each β ≥ 0,the function ?β,αde fined by is also nondecreasing. In this section,we present the local convergence of the inexact Newton method using(1.6)and(1.7). First,we consider the case Bn=F′(xn)for each n ≥ 0. Theorem 3.1Suppose that x?satis fies equation(1.1),F has a continuous Fr′echet derivative in U(x?,r),F′(x?)?1exists and F′(x?)F′satis fies the radius Lipschitz condition(1.6)and the center-Lipschitz condition(1.7).Assume that Bn=F′(xn)for each n ≥ 0 in(1.3)and with vn≤v<1.Let r>0 satisfy Then the method(INLM)(for Bn=F′(xn))is convergent for all x0∈ U(x?,r)and where is less than 1.Further,suppose that the function Lαde fined in(2.11)is nondecreasing for some α with 0<α≤1.Letsatisfy Then the method(INLM)(for Bn=F′(xn))is convergent for all x0∈U(x?,)and where is less than 1. ProofLet x0∈ B(x?,r),where r satis fies(3.1).Then q given by(3.3)is such that q∈(0,1).Indeed,by the positivity of L,we have Suppose that(notice that x0∈ U(x?,r))xn∈ U(x?,r),we have,by(1.3), where xθ=x?+θ(xn?x?).It follows,by Lemmas 2.1 and 2.2 and conditions(1.6)and(1.7)that we can obtain in turn In particular,if n=0 in(3.7),we obtainHence x1∈ U(x?,r),which shows that the method(INLM)can be continued an in finite number of times.By induction,for each n ≥ 0,xn∈ U(x?,r)anddecreases monotonically.Consequently,it follows that,for each n≥0, Hence we show(3.3).Moreover,ifsatis fies(3.4)and Lαde fined by(2.11)is nondecreasing for some α with 0< α ≤ 1,then we get If n=0 in(3.1),then we get Hence x1∈U(x?,?r).That is,the method(INM)can be continued an in finite number of times. It follows by induction that,for each n≥0,xn∈U(x?,)anddecreases monotonically.Therefore,for each k≥0,from(3.7)and Lemma 2.4,it follows in turn that Remark 3.2If L0=L,then our Theorem 3.1 reduces to Theorem 3.1 in[7].Otherwise,if L0 and which reduce to the ones in[19]if L0=L.Then we can conclude that vanishing residual,Theorem 3.1 merges into the theory of the Newton method.Besides,if the function Lαde fined by(2.11)is nondecreasing for α=1,then we improve the result in[7]. Next,we present a result analogous to Theorem 3.1 can also be proven for the inexact Newton-like method,where Bn=B(xn)approximates F′(xn). Theorem 3.3Suppose that x?satis fies equation(1.1),F has a continuous derivative in U(x?,r),F′(x?)?1exists and F′(x?)F′satis fies the radius Lipschitz condition(1.6)and the center Lipschitz condition(1.7).Let B(x)be an approximation to F′(x)for all x ∈ U(x?,r),B(x)is invertible and Then the method(INLM)method is convergent for all x0∈ U(x?,r)and where is less than 1.Further,suppose that the function Lαde fined by(2.11)is nondecreasing for some α with 0<α≤1.Lersatisfy Then(INLM)is convergent for all x0∈U(x?,)and where is less than 1. ProofLet x0∈ U(x?,r),where r satis fies(3.9),then q given by(3.11)is such that q∈(0,1).Indeed,by the positivity of L,we have Moreover,if xn∈ U(x?,r),then,from(1.3),it follows in turn that where xθ=x?+θ(xn?x?).Using Lemmas 2.1,2.2 and condition(3.8),we obtain If n=0 in(3.15),then we obtain Hence x1∈ U(x?,r),this shows that the iteration can be continued an in finite number of times. By induction,for each n ≥ 0,xn∈ U(x?,r)anddecreases monotonically. Therefore,for each n≥0,it follows in turn that which implies(3.10).Furthermore,ifsatis fies(3.12)and Lαde fined by(2.11)is nondecreasing for some α with 0< α ≤ 1,then we get If n=0 in(3.15),then we obtain Hence x1∈U(x?,),this shows that(1.4)can be continued in finite number of times.By induction,for eachanddecreases monotonically. Therefore,for each n≥0,we have Remark 3.4If L0=L our Theorem 3.3 reduces to Theorem 3.2 in[7].Otherwise,i.e.,if L0 In this section,we consider the following special cases of Theorem 3.1 and Theorem 3.3,respectively. Corollary 4.1Suppose that x?satis fies equation(1.1),F has a continuous derivative in U(x?,r),F′(x?)?1exists,F′(x?)F′satis fies the radius Lipschitz condition with for each x ∈ U(x?,r),0≤ θ≤ 1,where xθ=x?+θ(x?x?),and the center-radius Lipschitz condition with for each x∈ U(x?,r),0≤ θ≤ 1 for some c0≤ c.Assume that Bn=F′(xn)for each n≥ 0 in(1.3)and with vn≤v<1.Let?r>0 satisfy Then the inexact Newton method is convergent for all x0∈U(x?,)and where is less than 1. Corollary 4.2Suppose that x?satis fies equation(1.1),F has a continuous derivative in U(x?,r),F′(x?)?1exists and F′(x?)F′satis fies the radius Lipschitz condition(4.1)and the center Lipschitz condition(4.2).Let B(x)be an approximation to the F′(x)for all x ∈ B(x?,r)B(x)is invertible and satis fies condition(3.8), with vk≤v<1.Let>0 satisfy Then the inexact Newton method is convergent for all x0∈U(x?,)and where is less than 1. Remark 4.3(1)If v=0 in Corollary 4.1,then the estimate for the radius of convergence ball for Newton’s method is given by which improves the result in[7]for c0 (2)The results in Section 5 of[7]using only the center-Lipschitz condition can be improved if rewritten using L0instead of L. Finally,we provide an example where L0 Example 5.1Let X=Y=R3,D=(0,1)and x?=(0,0,0).De fine function F on D for w=(x,y,z)by Then the Fr′echet derivative of F is given by Notice that we have F(x?)=0,F′(x?)=F′(x?)?1=diag{1,1,1}and L0=e?1 More examples where L0 Under the hypothesis that F′(x?)F′satis fies the center Lipschitz condition(1.7)and the radius Lipschitz condition(1.6),we presented a more precise local convergence analysis for the enexact Newton method under the same computational cost as in earlier studies such as Chen and Li[7].Numerical examples are provided to show that the center Lipschitz function can be smaller than the radius Lipschitz function.2 Background

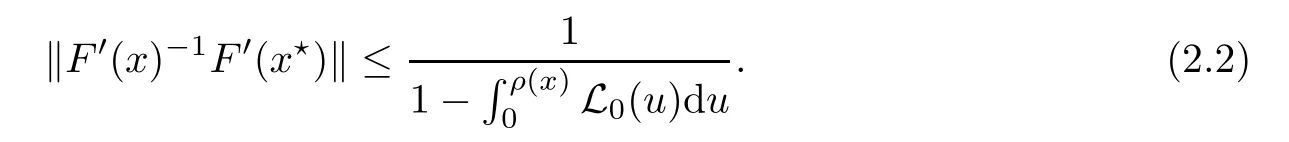
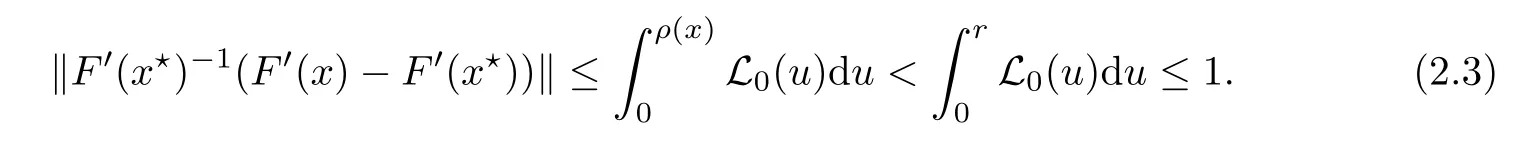
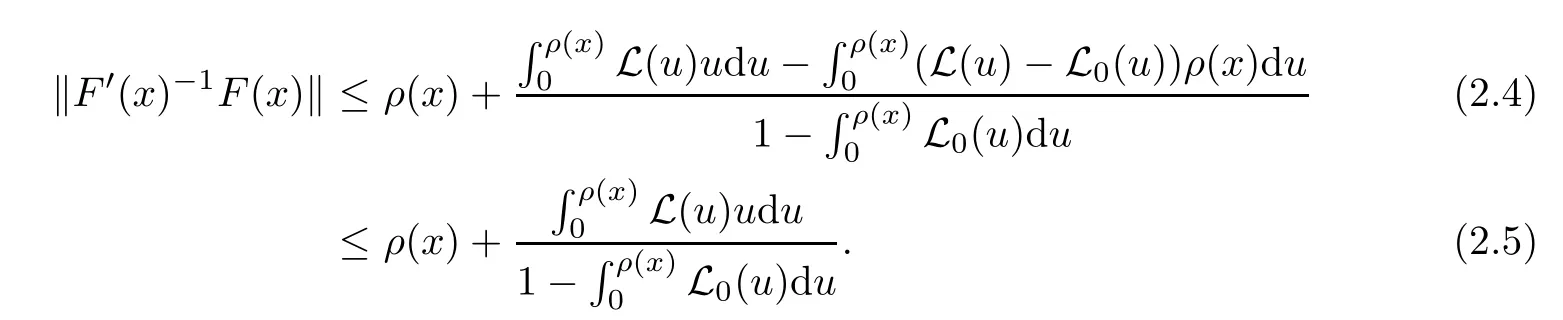
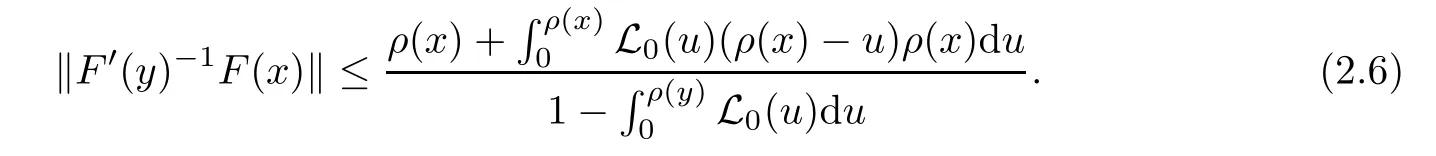
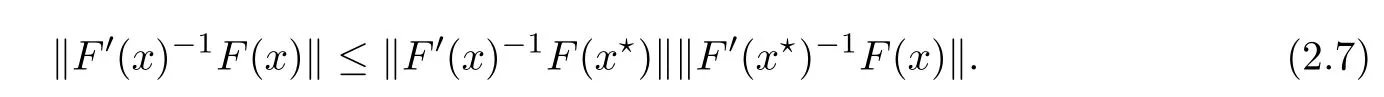
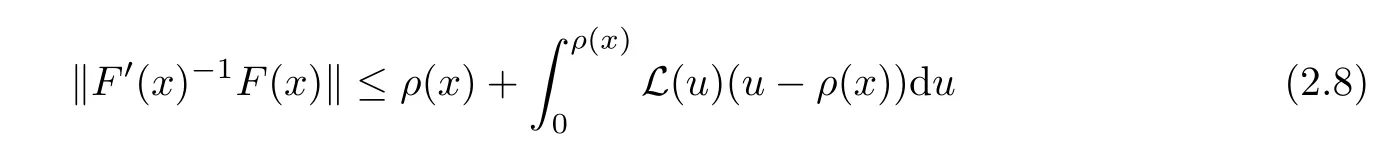
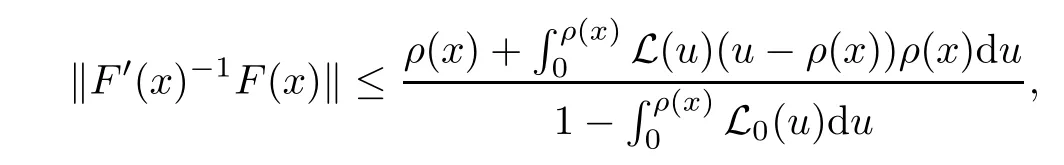
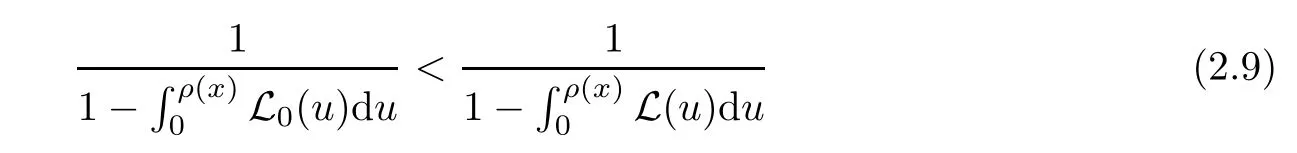
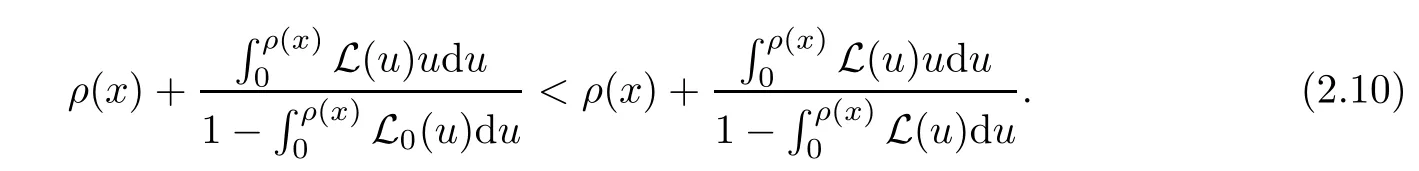

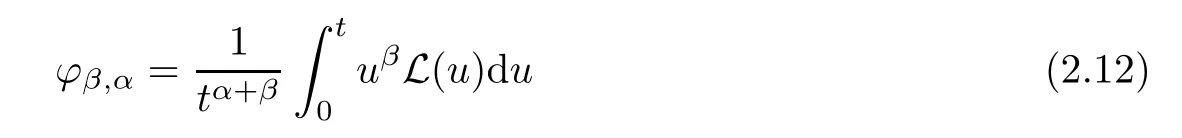
3 Local Convergence
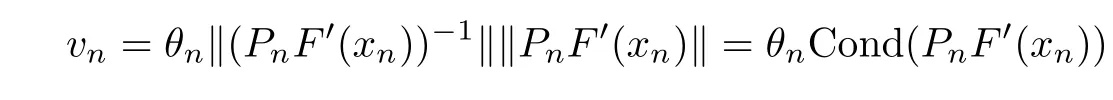


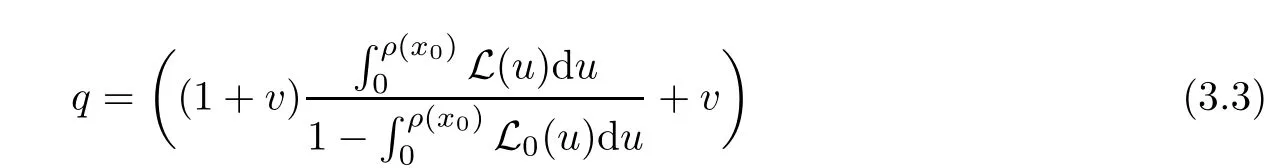

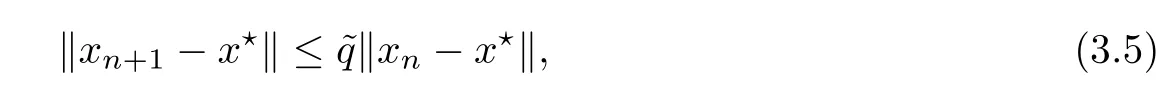
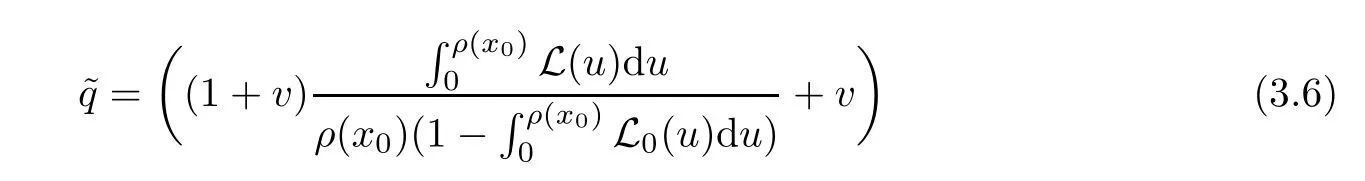
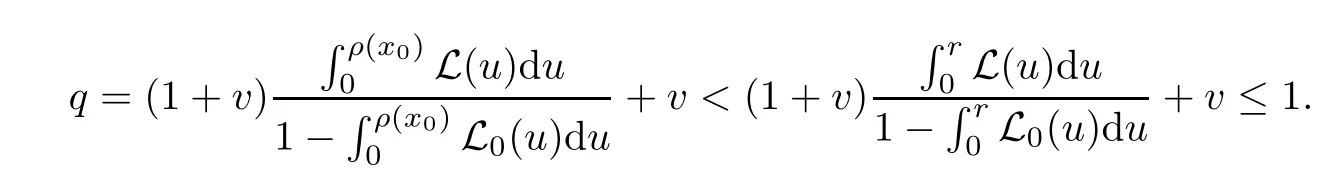


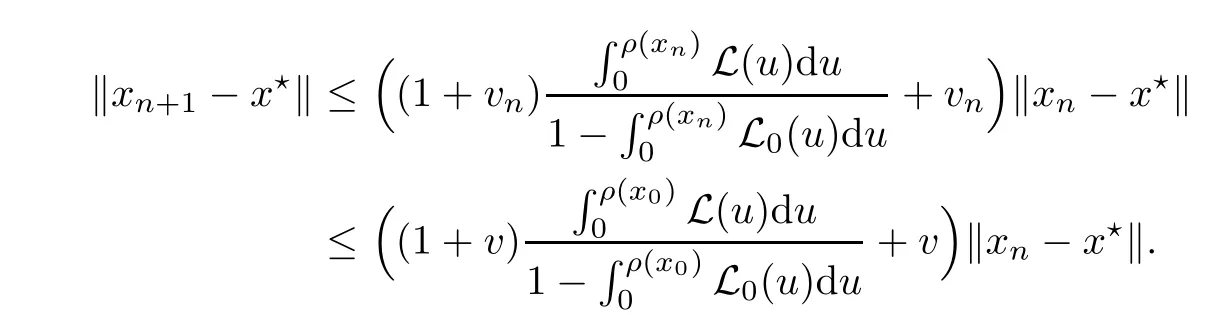
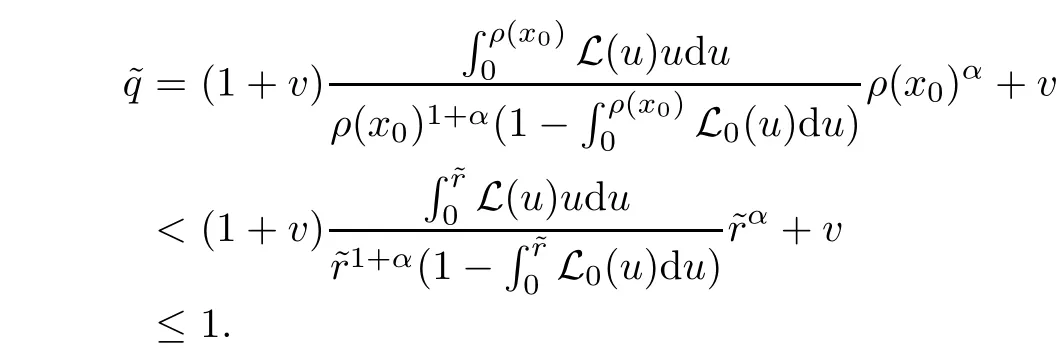

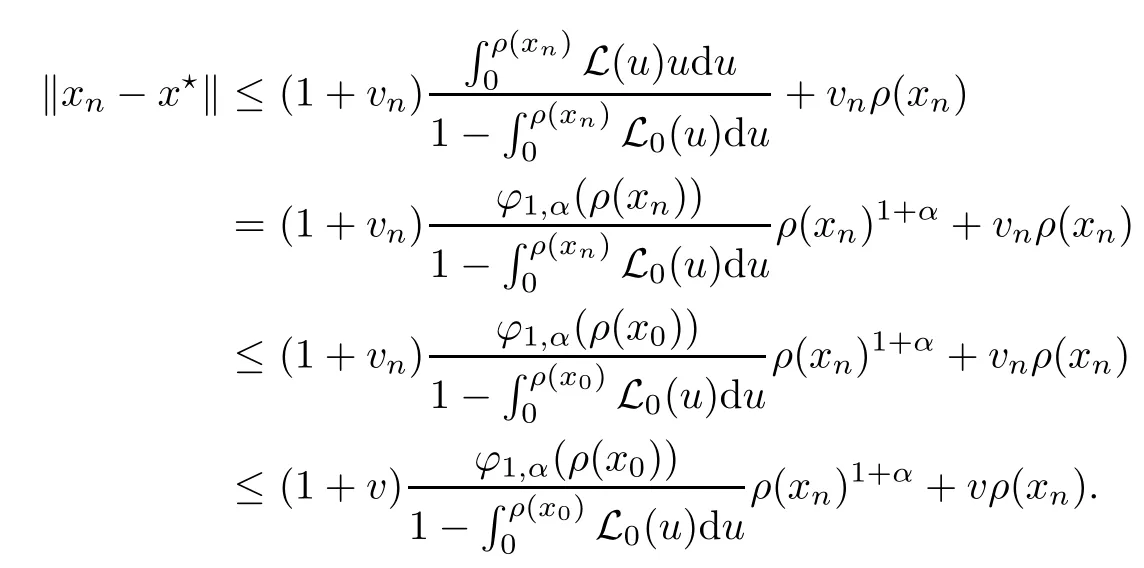

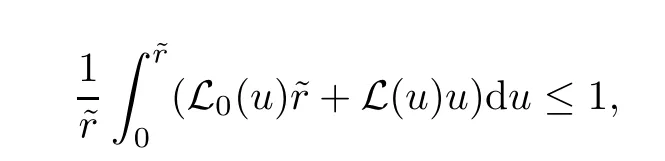
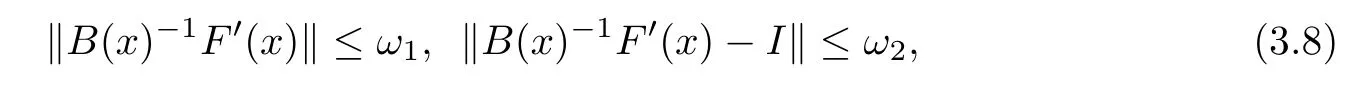
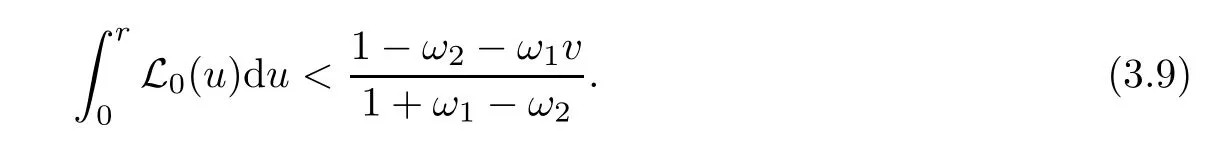

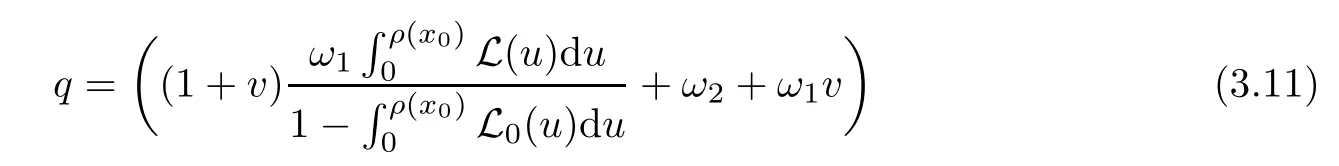
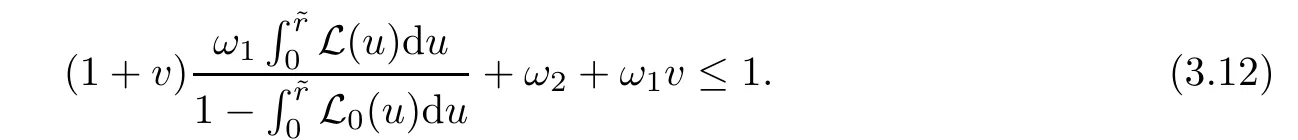

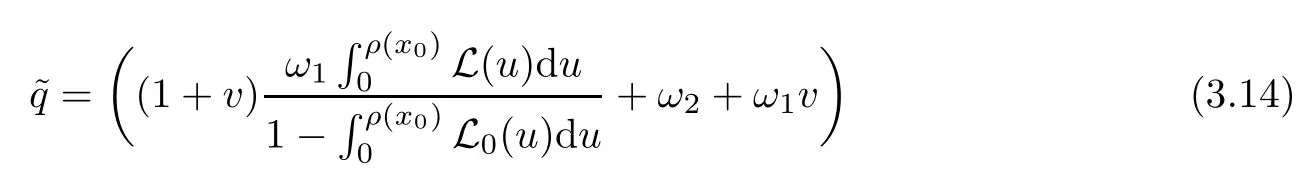
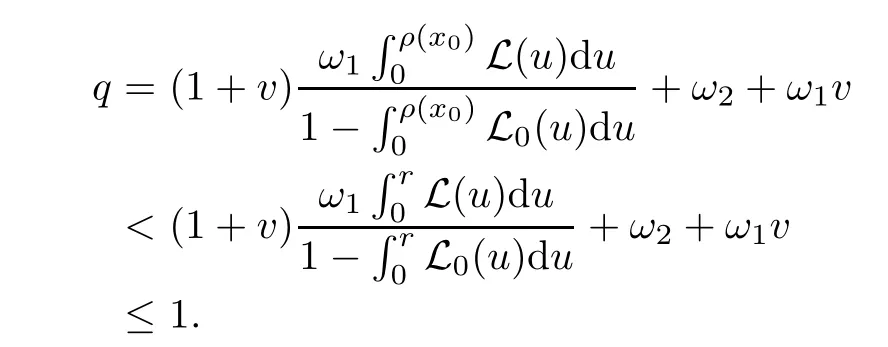
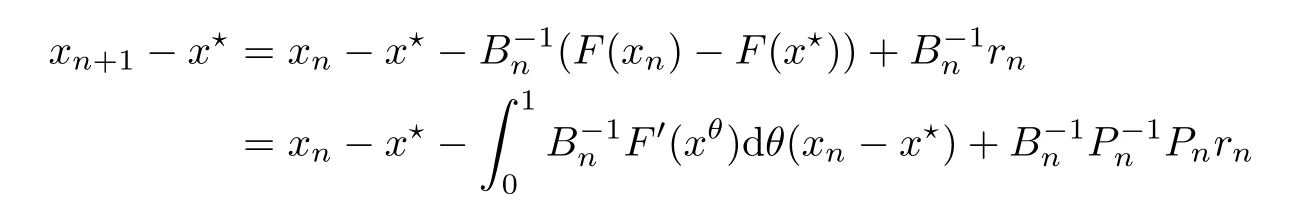
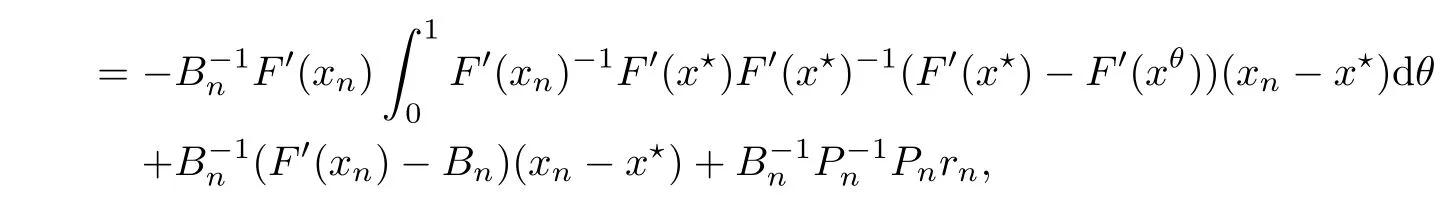
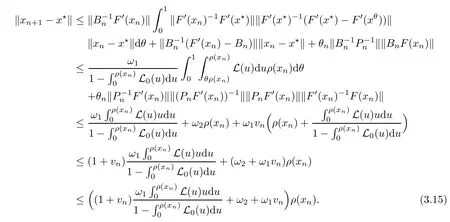
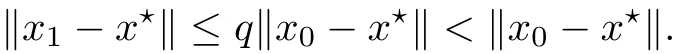
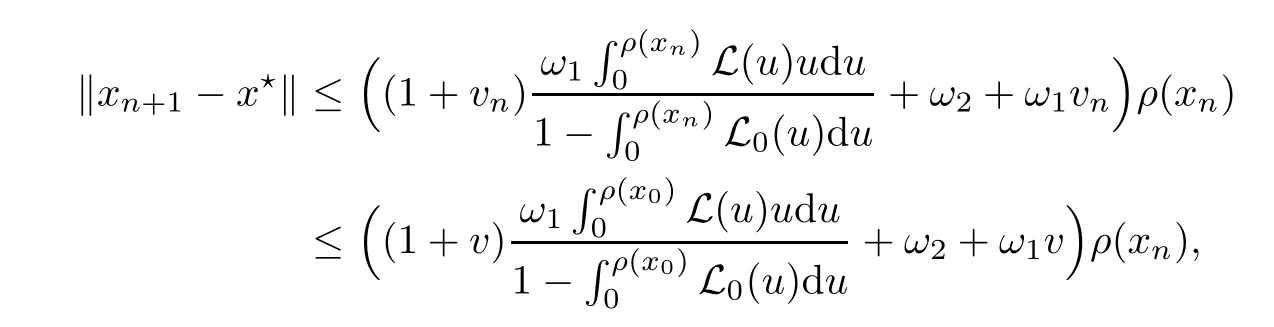

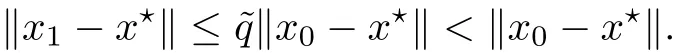
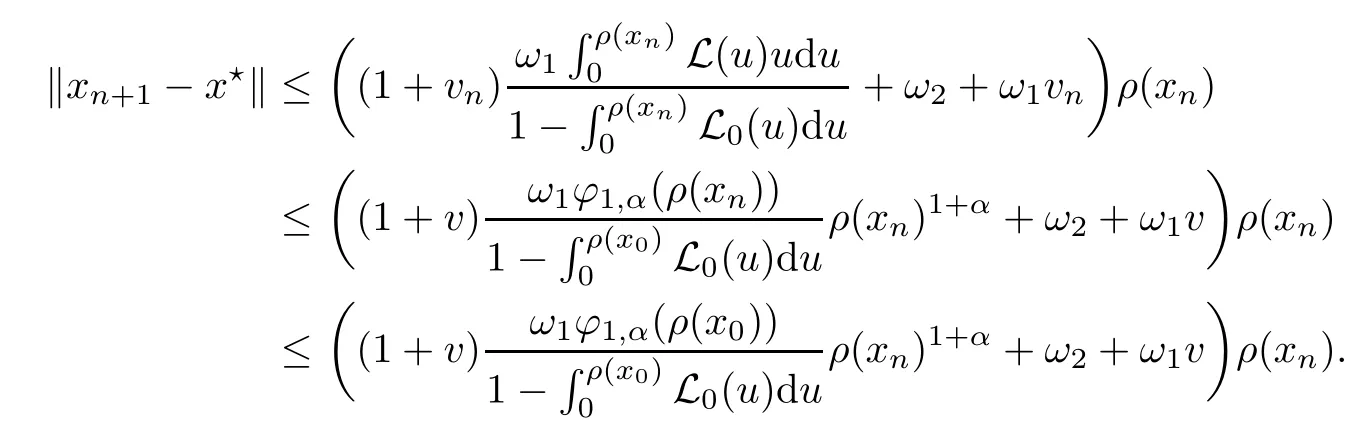
4 Special Cases
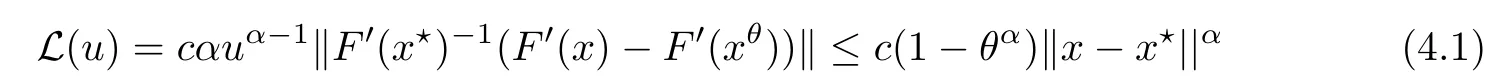
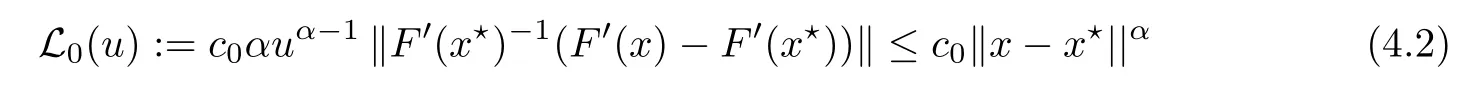
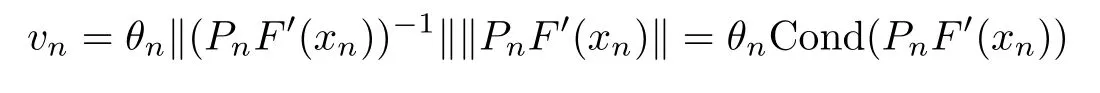
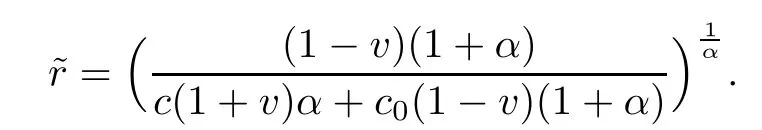
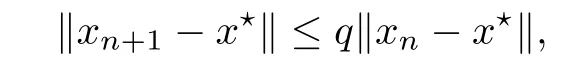
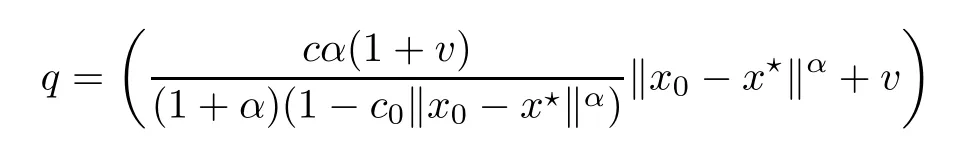
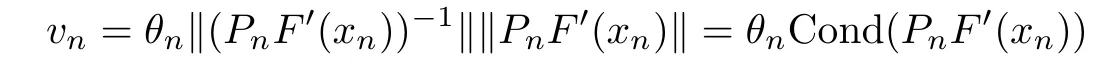
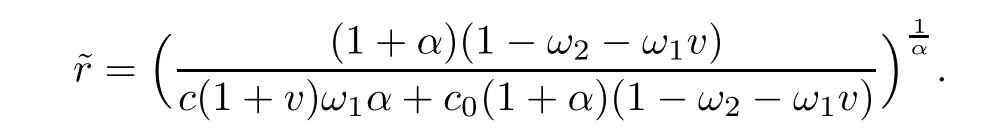
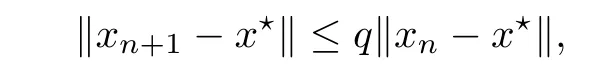

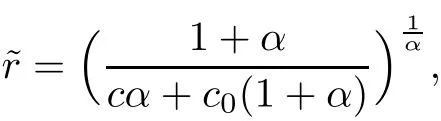
5 Examples
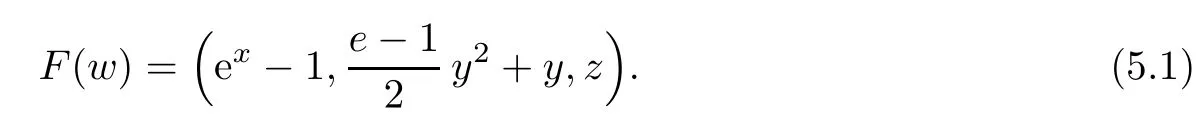
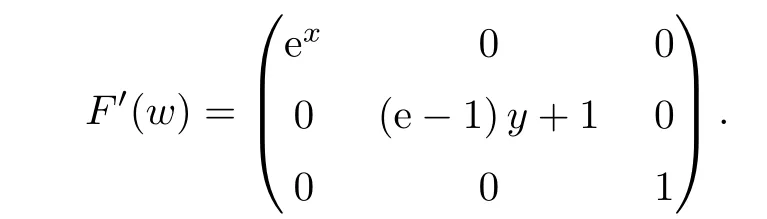
6 Conclusions
 Acta Mathematica Scientia(English Series)2020年1期
Acta Mathematica Scientia(English Series)2020年1期
