BOUNDEDNESS OF MULTILINEAR LITTLEWOOD-PALEY OPERATORS ON AMALGAM-CAMPANATO SPACES?
Xiang LI(李翔) Qianjun HE(何騫君) Dunyan YAN(燕敦驗(yàn))
1.School of Mathematical Sciences,University of Chinese Academy of Sciences,Beijing 100049,China
2.School of Applied Science,Beijing Information Science and Technology University,Beijing 100192,China
E-mail:lixiang162@mails.ucas.ac.cn;heqianjun16@mails.ucas.ac.cn;ydunyan@ucas.ac.cn
Abstract In this paper,we consider the boundedness of multilinear Littlewood-Paley operators which include multilinear g-function,multilinear Lusin’s area integral and multilinear Littlewood-Paley -function.Furthermore,norm inequalities of the above operators hold on the corresponding Amalgam-Campanato spaces.
Key wordsmultilinear Littlewood-Paley g-function;multilinear -function;Amalgam-Campanato spaces
1 Introduction
Since the pioneering work of Coifman and Meyer[4,5],multilinear theory attracted much attention,including Christ and Journ′e[3],Fu et al.[8],Kenig and Stein[16],Grafakos and Torrers[9,10],Hu[15]and Lerner et al.[18].As a multilinearization of Littlewood-Paley’s function,Coifman and Meyer[6]introduced the following bilinear operator
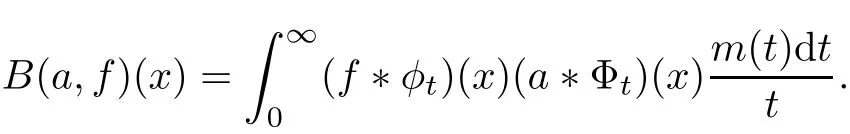

Recently,in[2,23,29,30],the authors de fined and studied the multilinear Littlewood-Paley operators,including multilinear g-function,Marcinkiewicz integral and-function.To state some known results,we first recall some de finitions.
De finition 1.1A function K(x,y1,···,ym)de fined away from the diagonal x=y1=···=ymin(Rn)m+1is said to be a multilinear non-convolutiontype kernel,if for all(y1,···,ym)∈(Rn)m,there exists a positive constant C,such that K satis fies the following three conditions Z
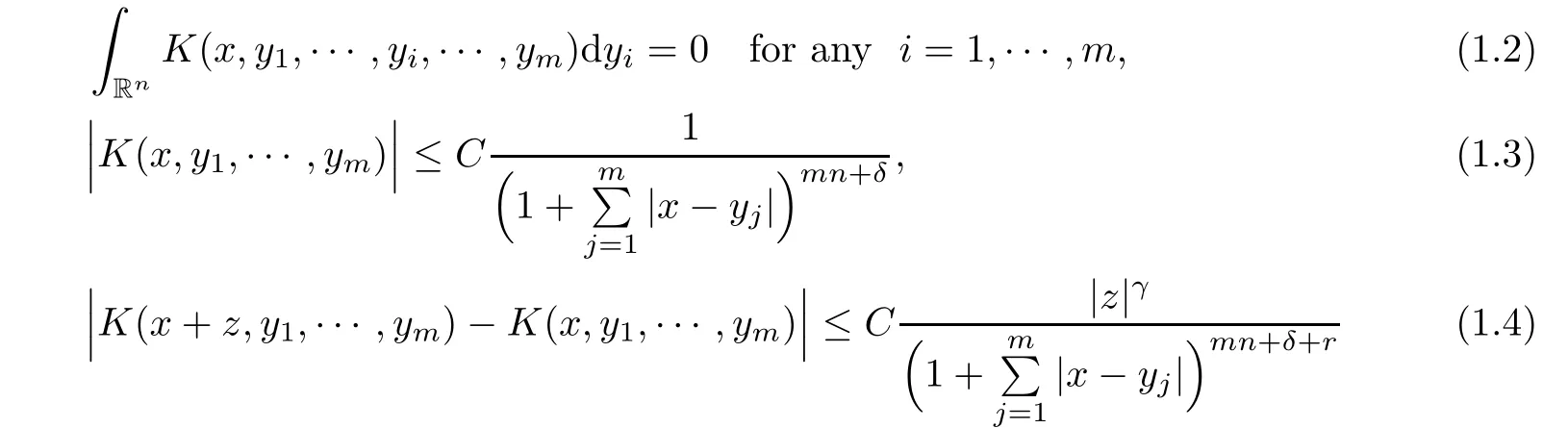
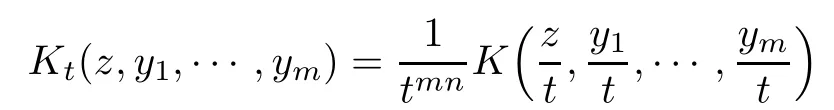
and

Then the multilinear Littlewood-Paley g-function,multilinear Lusin’s area integral and multilinear Littlewood-Paley-function with non-convolution type kernels are de fined by
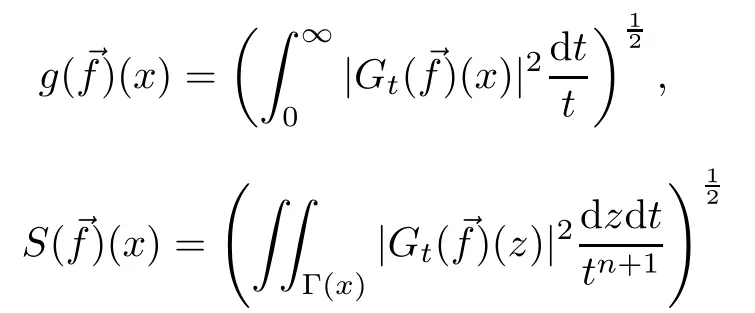
and
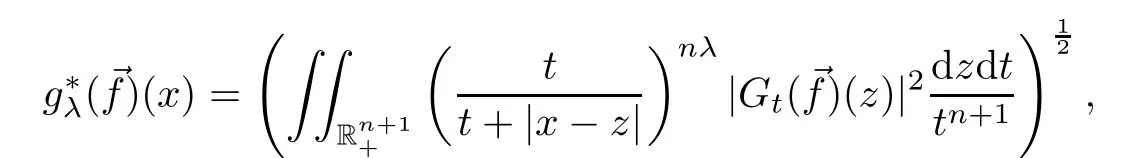
We need the following two results given by Xue and Yan[30].
Theorem AAssume that 1 Theorem BAssume that λ >2m,0< γ To state our results,we now recall the de finition of Amalgam-Campanato space which appears in[28]. De finition 1.2(Amalgam-Campanato space)Let n<β<∞and 0 with where fB(y,r)denotes the average of f over ball B(y,r)with radii r and centered at y,that is, Remark 1.3It is easy to see that the spaces goes back to the classical Campanato spacewhen p=∞. In this paper,we only consider the bilinear case,the multilinear case m>2 can be obtained in the similar way.Our main results are as follows. Theorem 1.4Let n<βj<∞,1 Theorem 1.5Let λ>4,n<βj<∞,qj≤ αj≤pj≤ ∞ with j=1,2.Assume that Suppose that If g?λ(f1,f2)(x)is finite on a set of positive measure,then these exists a positive constant C independent of f1,f2such that Remark 1.6Notice that S(f1,f2)(x)≤Cg?λ(f1,f2)(x)point-wisely holds[24],and thus the above result is also true for multilinear Lusin’s area integral S. This paper is organized as follows.Section 2 will prepare some lemmas.The proof of Theorem 1.4 will be show in Section 3.Section 4 will be devoted to prove Theorem 1.5. Throughout this paper,we use the following notation.For 1≤ p≤ ∞,p′is the conjugate exponent of p,that is,1/p+1/p′=1.The notation A.B stand for A ≤ CB,for some positive constant C independent of A and B.The set B=B(y,r)denotes an open ball with center at y and radius r,and 4B denote the ball with the same center as B and with radius length 4r.The letter C will denote a constant which may be different in each occasion but is independent of the essential variables. In order to prove the main results,we need some preliminaries and lemmas. Lemma 2.1Assume that f ∈ (Cq,Lp)α,β,1 ≤ p,q ≤ ∞.If γ >0 and δ>0,then for any B=B(y,r),we have ProofUsing H?lder’s inequality,we obtain that The following lemma plays a key role in our proof. Lemma 2.2Assume that f ∈ (Cq,Lp)α,β,n< β < ∞,1≤ q≤ α ≤ p≤ ∞,If ε>0 and,then for any B=B(y,r),we have ProofWe first split the following integral into two parts as follows, We first estimate of I.It implies from H?lder’s inequality that Taking Lpnorm of the first part of(2.1),we obtain that To estimate II,we need the following estimate Since we have By(2.5)and Minkowski’s inequality,we obtain Next,we will deal with f1and f2,the programing is following[14].We decompose fi,i=1,2,as follows Then one gets g(f11,f2j)=g(f1j,f21)=0 by condition(1.2)for j=1,2,3.We shall use the following notations.For any nonnegative integer k,denote De fine and We need the following Lemma for. Lemma 2.3Assume that α,β,p and q as in Theorem 1.5.For any r>0,we have ProofTo prove inequality(2.8),by condition(1.3),we have As t Next,we give the proof of(2.10).Note that(f13,f23)can be controlled by a constant times of Since t<4r,y1,y2∈(4B)c,z∈B(y,),we have Thus,taking By H?lder’s inequality and Lemma 2.2,we obtain where we used the fact and Prove of inequality(2.10),when(z,t)∈J(k),we havet2kr≤1,and if λ1> λ2>4.Therefore,choosing λ ∈ (4,5)and using(1.3),we get In order to deal with the integral that contains f2,we first split the integral interval(4B)cinto(4B)c∩(2k+1B)cand(4B)c∩(2k+1B),then we magnify each of the two intervals to(4B)c∩(2k+1B)cand 2k+1B,respectively, fi nally,we get For y2∈ (2k+1B)c,z ∈ 2k?2B2k?3B and 2k?3r ≤ t<2k?2r,we obtain that t+|z? y2|~2kr+|y?y2|.Thus Using Minkowski’s inequality and Lemma 2.2,we obtain It remains to control II.In fact,it is easy to get Note that the first integral of(2.12)can be estimated Thus,we have To prove inequality(2.11),using similar way of(f12,f23)(x),we can conclude that Combining(2.12)with(2.13)and(2.14),it yields that We also need the following lemma. Lemma 2.4Assume that α,β,p and q as in Theorem 1.5.For any r>0,we have the following estimate ProofUsing the triangle inequality,we have Utilizing Lemma 2.3,we obtain Again by(1.3)of K and the mean value theorem,we have Similar to the estimate for Lemma 2.3,we conclude that where Similar to the proof of(2.10),we get By means of Minkowski’s inequality and Lemma 2.2,we get Similar to the proof of(2.10)for II,we obtain Take advantage of Lemma 2.2 and Minkowski’s inequality,we get Using symmetry,we also have Now,we will dealing with IV.By Minkowski’s inequality,we have By the Cauchy-Schwartz inequality,we have Hence,we get Combining(2.13)with(2.15)and by Minkowski’s inequality,we obtain where we used Proof of Theorem 1.4Using Minkowski’s inequality,we obtain the following estimate For the second term,by Minkowski’s inequality,we obtain According to(1.4)of K,for any x∈B,z1∈4B,z2∈(4B)c,we conclude that Hence, As a consequence,by H?lder’s inequality and Lemma 2.1,we obtain Similarly,we can conclude that Next we estimate the fourth term.Since,we can take ε satisfy condition Thus,using the estimated for the second term and H?lder’s inequality,we have The above inequality gives Taking Lp-norm on both side yields De fine Similar to the estimate of I1(y,r),it follows that Taking Lp-norm on both side inequality above,we obtain Let Similar to I2(y,r),we have and Taking Lp-norm on both side gives Using Minkowski’s inequality,we get This completes the proof of Theorem 1.4. Proof of Theorem 1.5Let fi=fi1+fi2+fi3,i=1,2 as in(2.7).Notice that(f11,f2j)=(f1j,f21)=0 for j=1,2,3,and by Minkowski’s inequality,we have Utilizing Lemma 2.3,we see that By symmetry,we also have Combining(4.1),(4.2)with(4.3)and Lemma 2.4,it yields that This completes the proof of Theorem 1.5.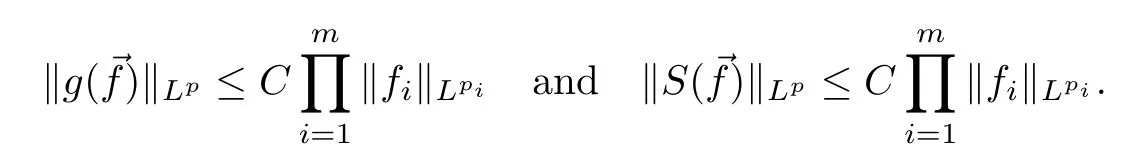
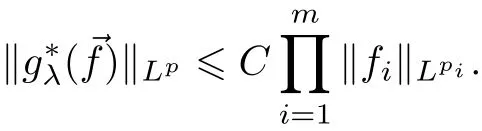
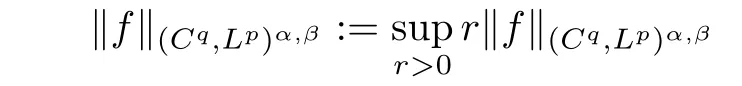
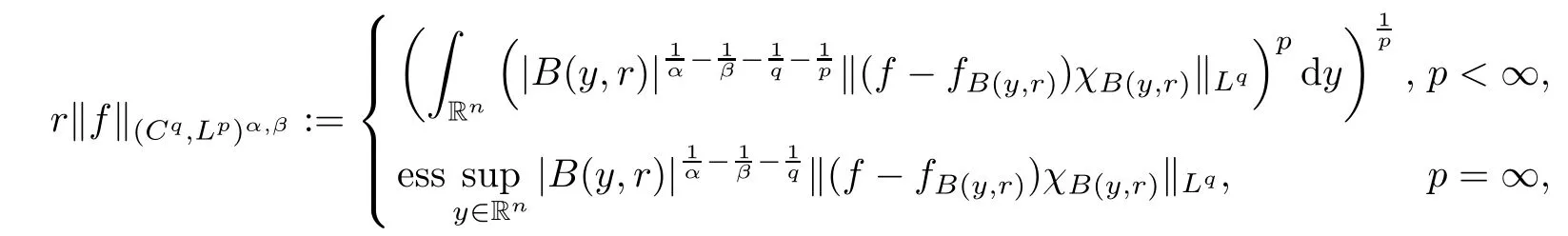
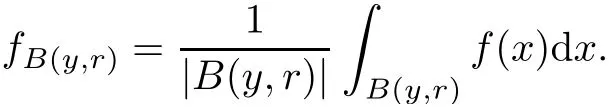
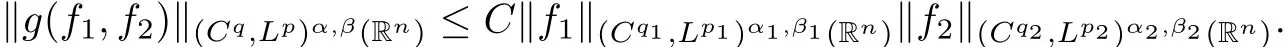
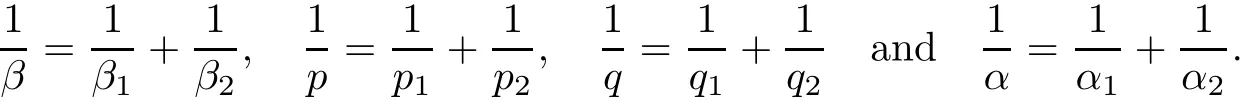
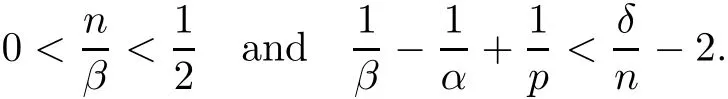

2Some Lemmas


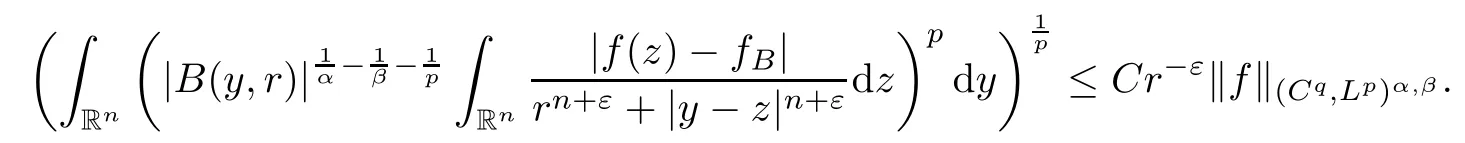
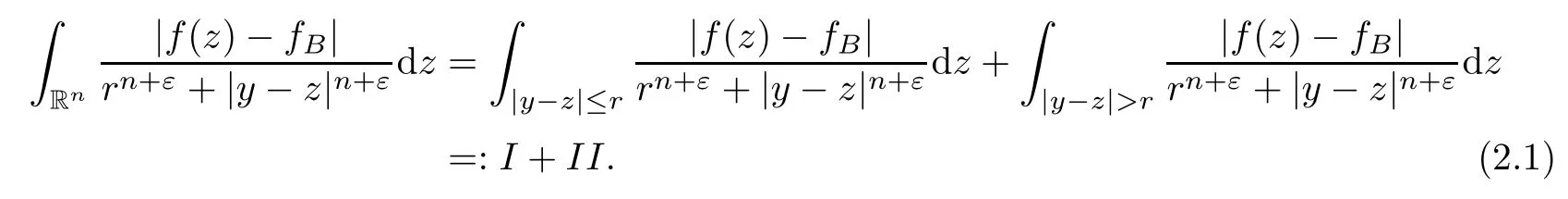


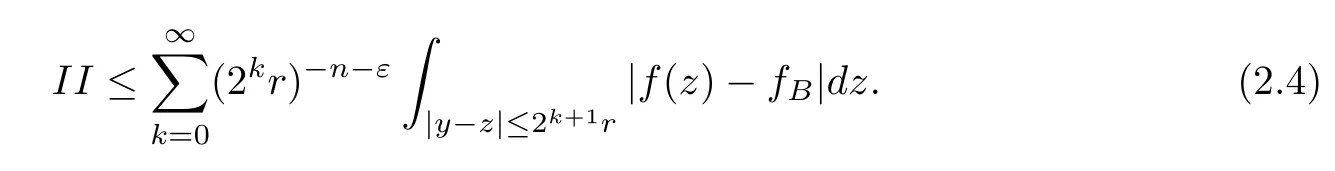
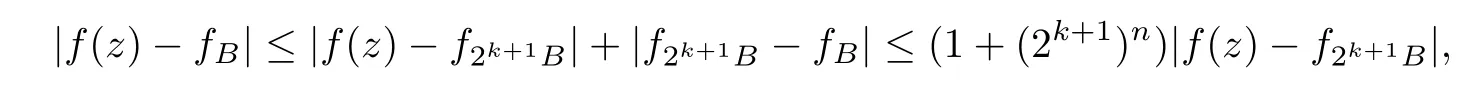
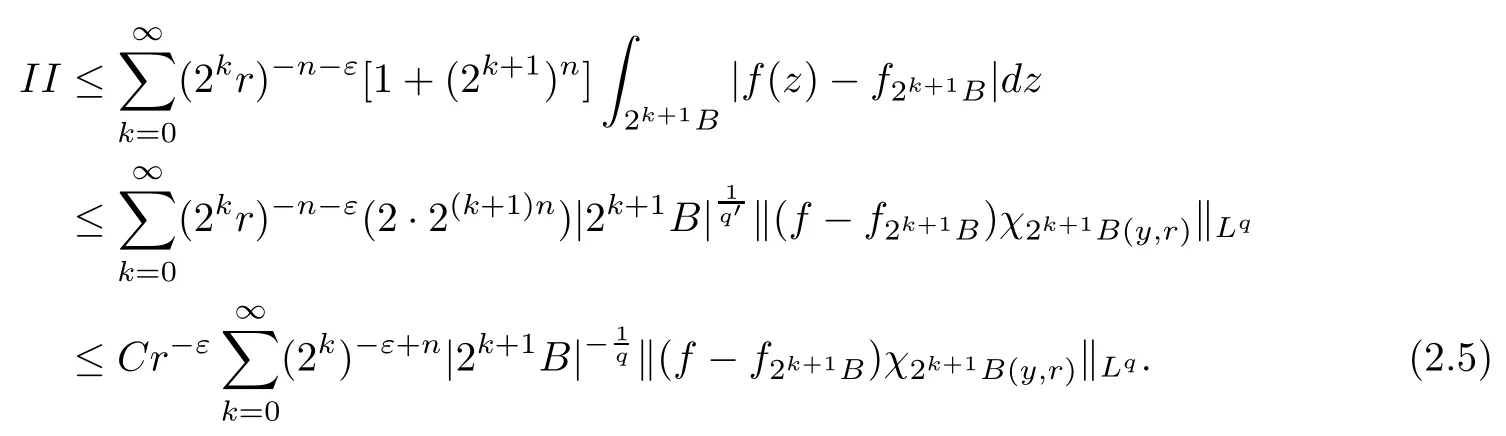
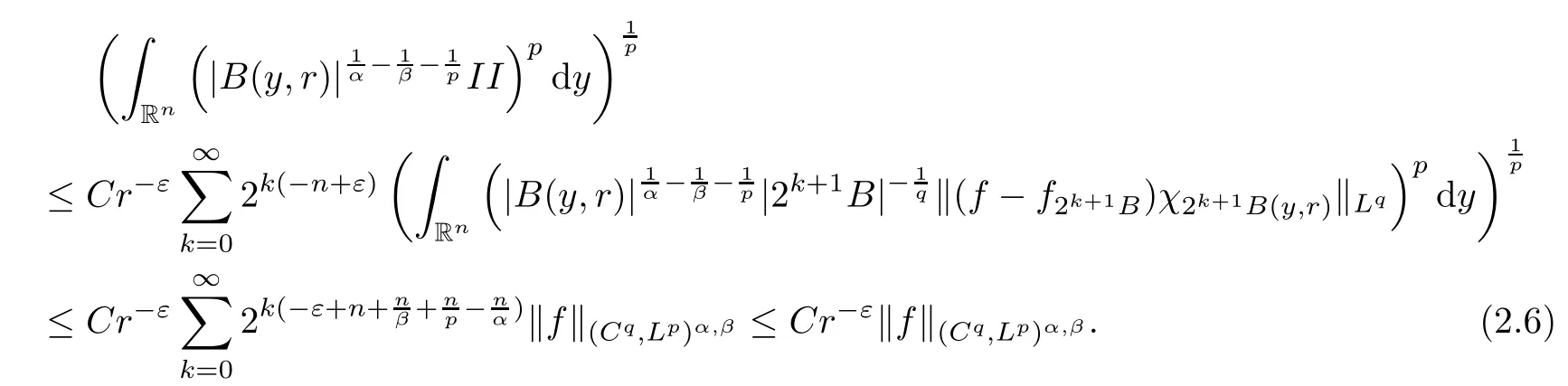

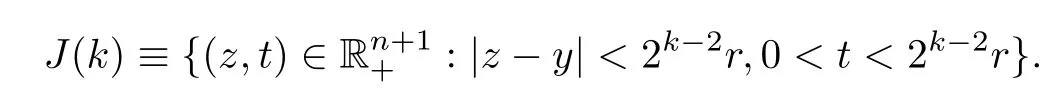
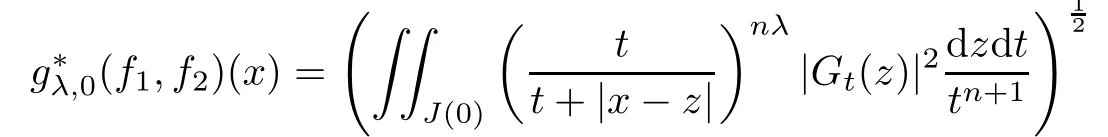

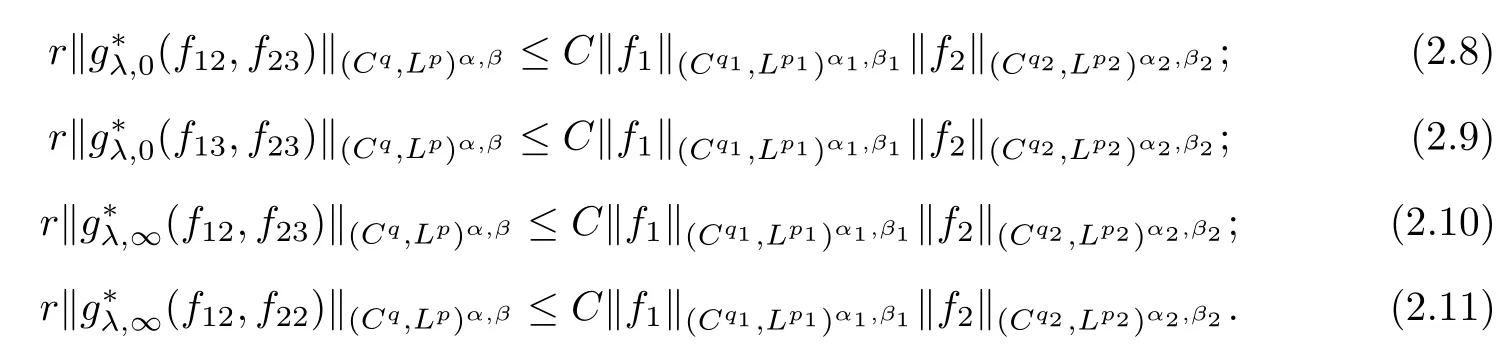

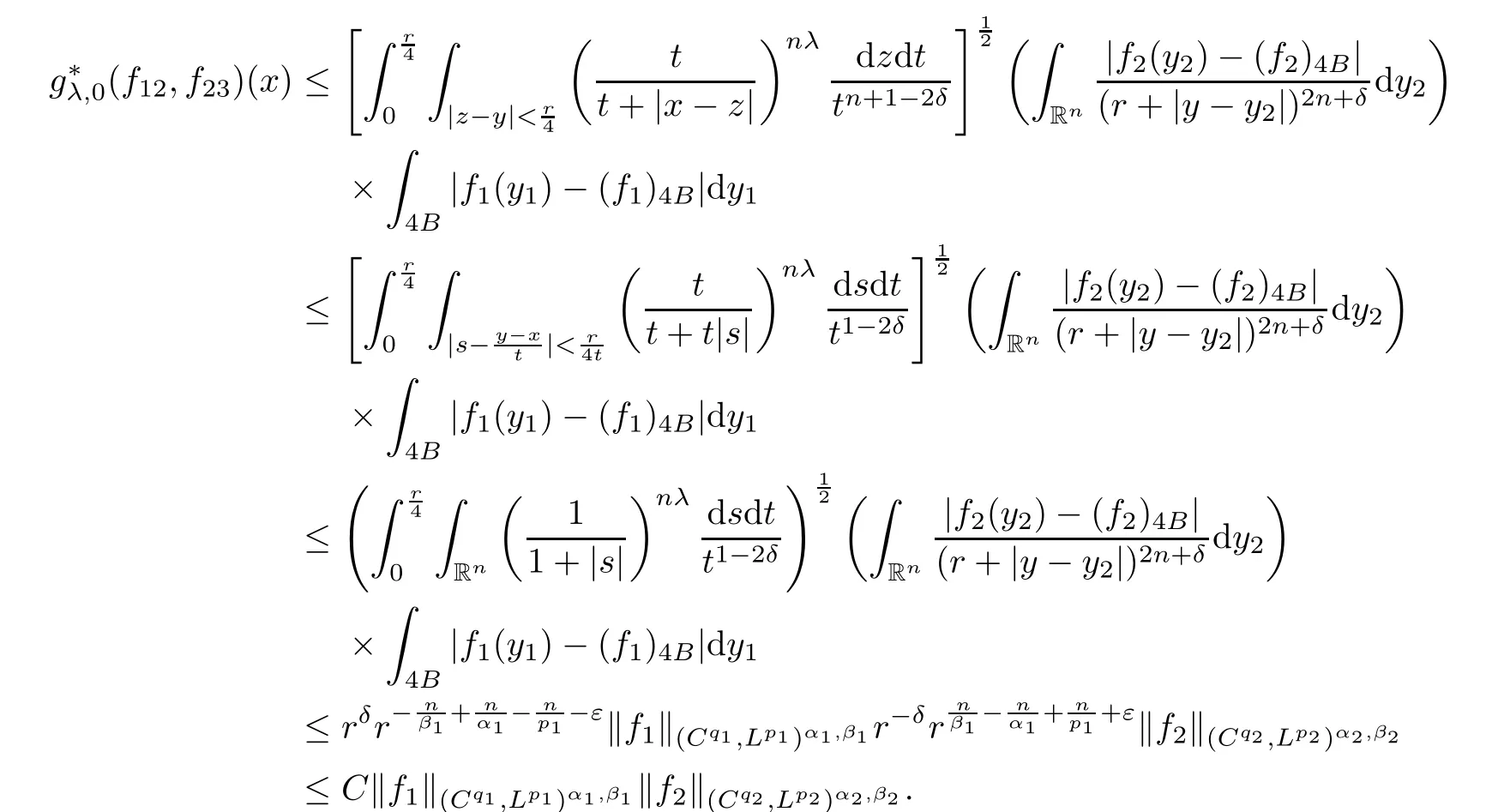
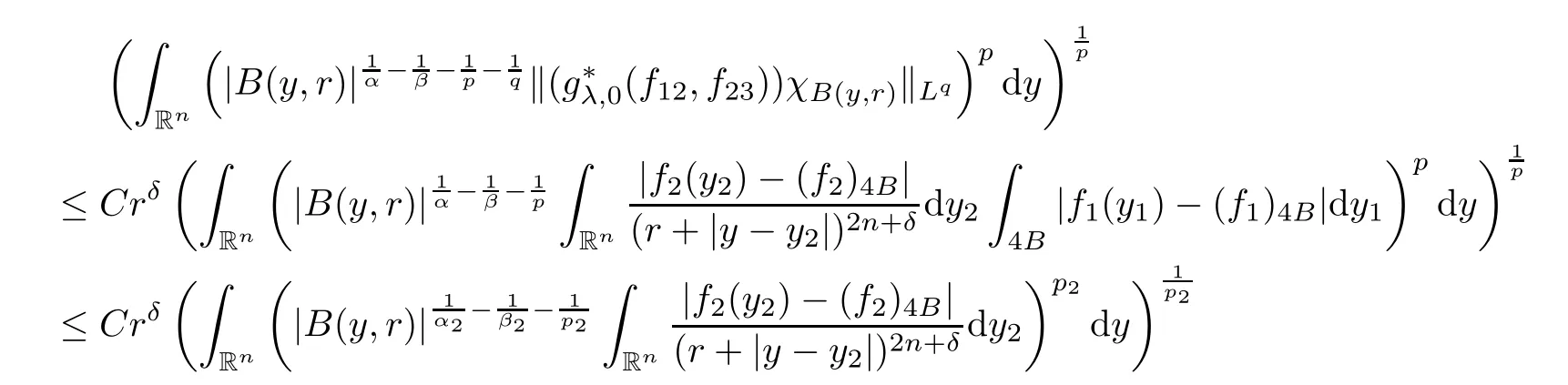

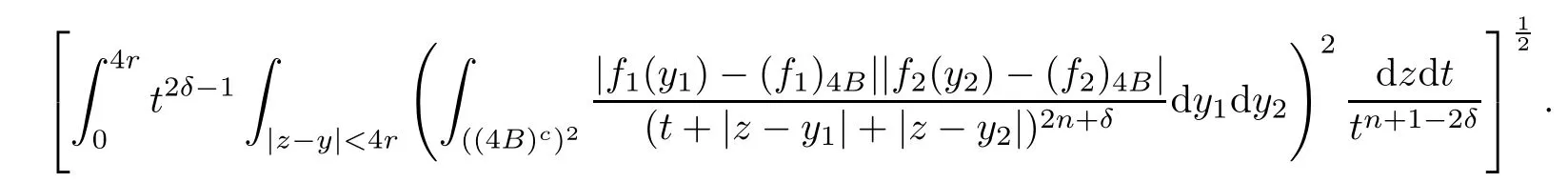
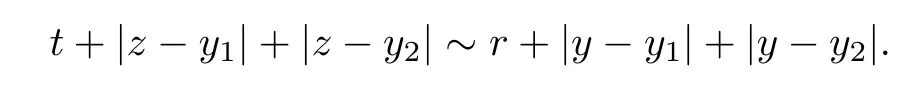
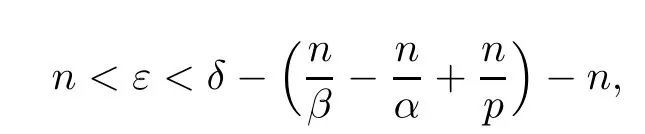


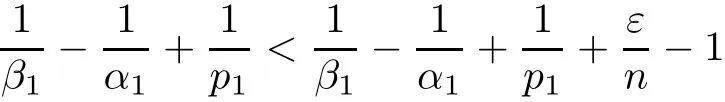
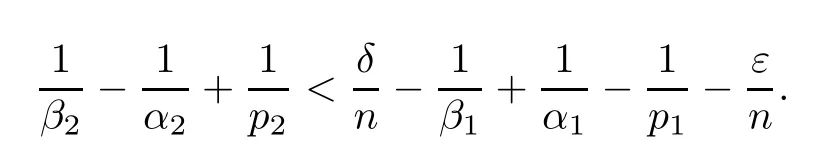
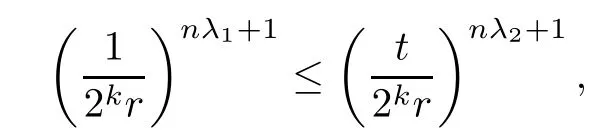
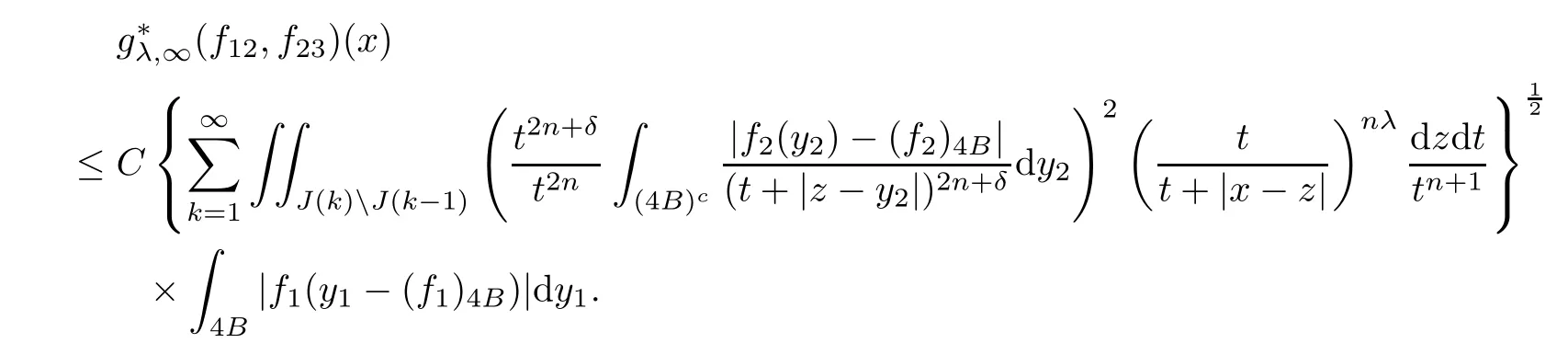
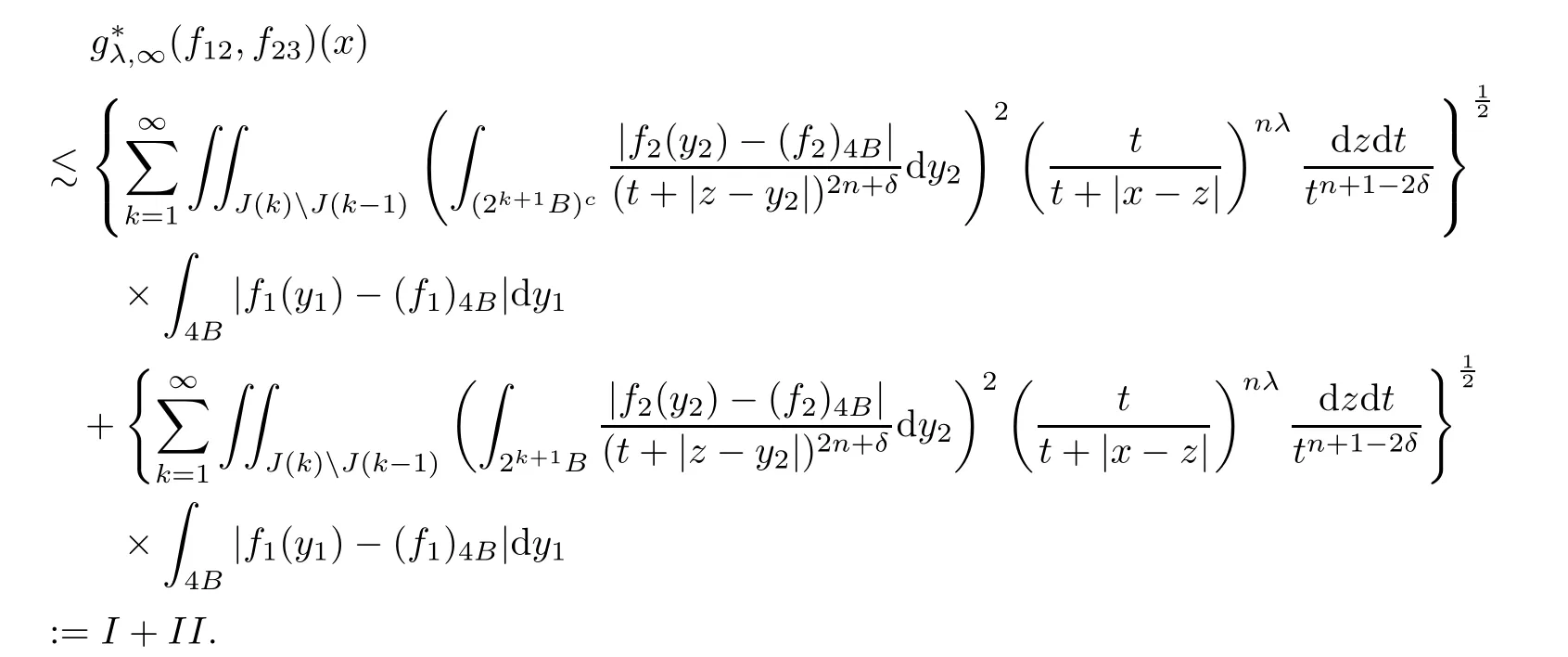
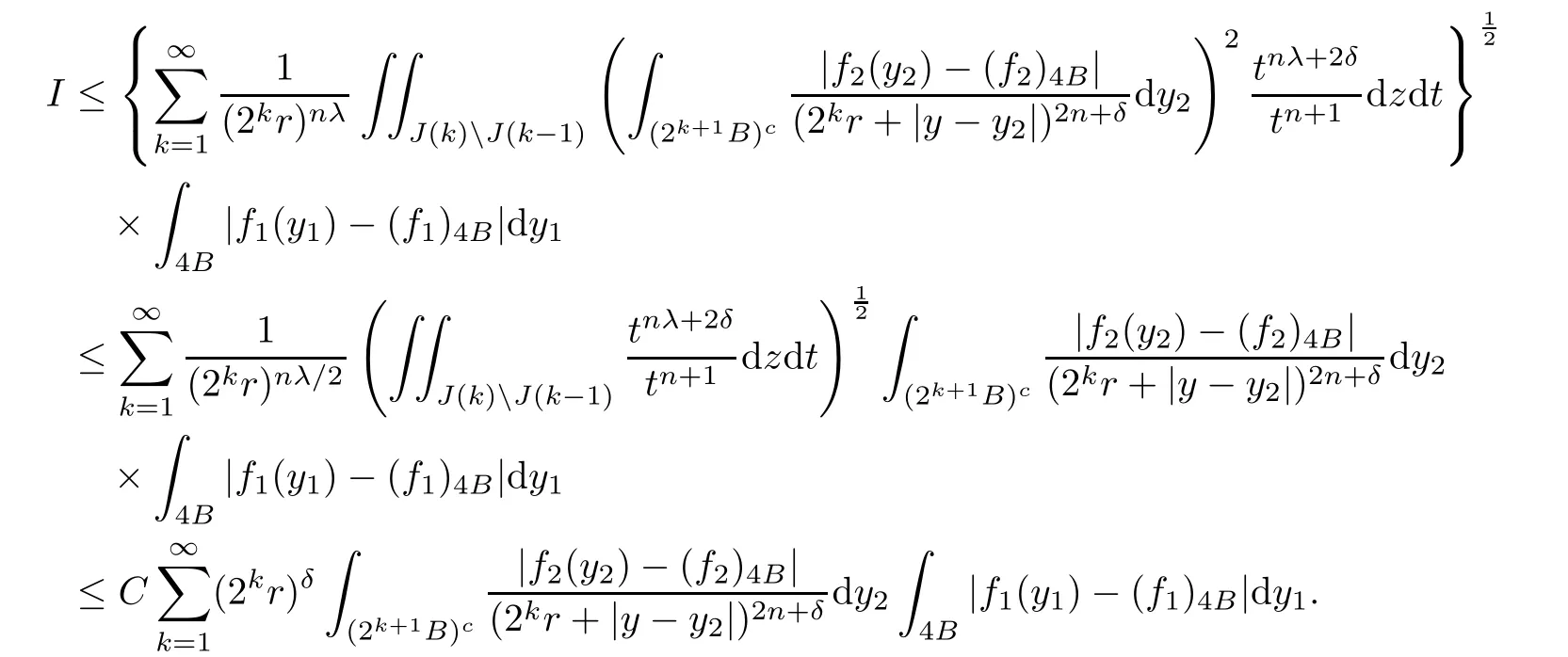

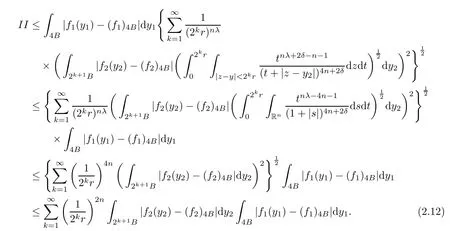

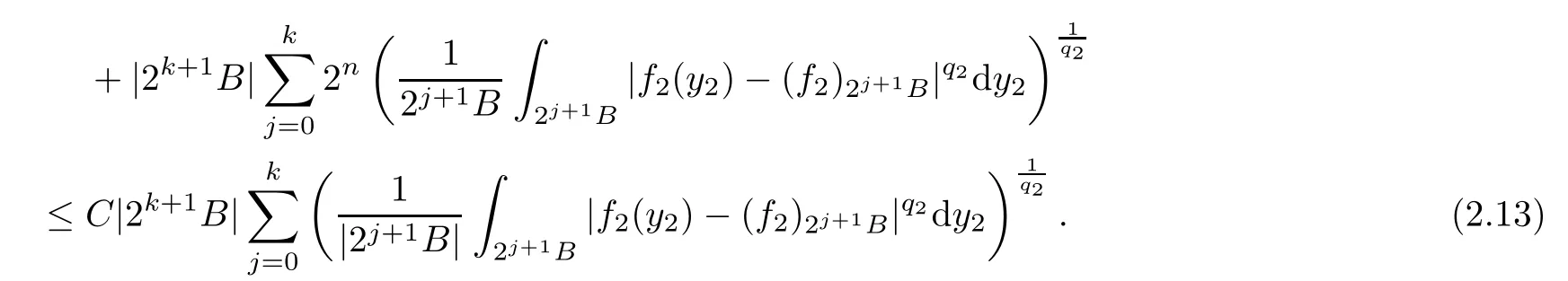
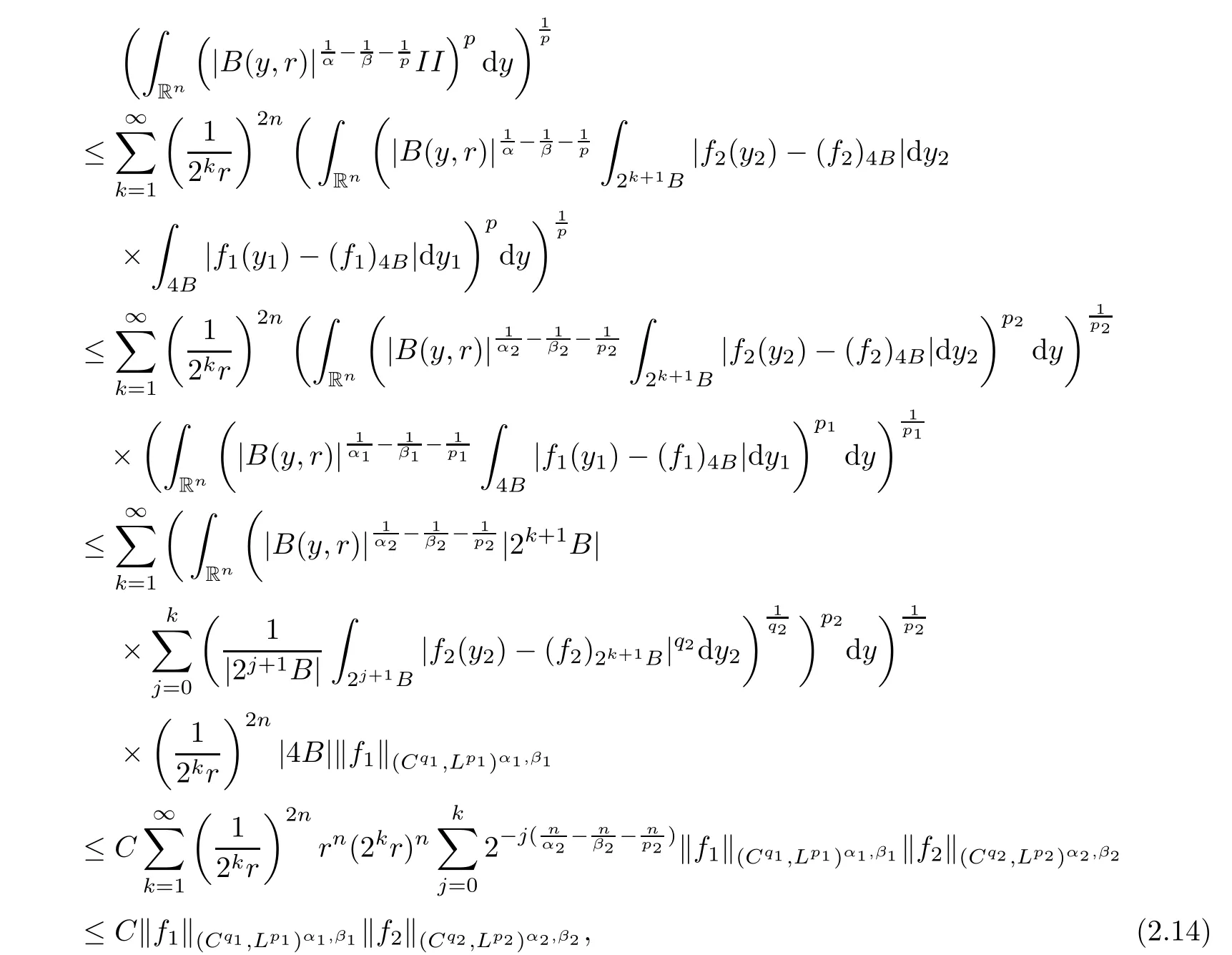
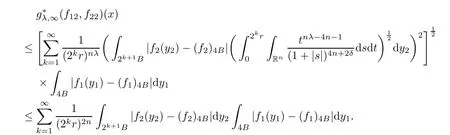
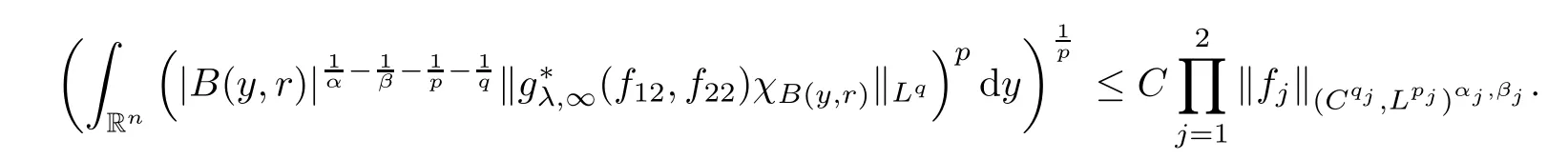
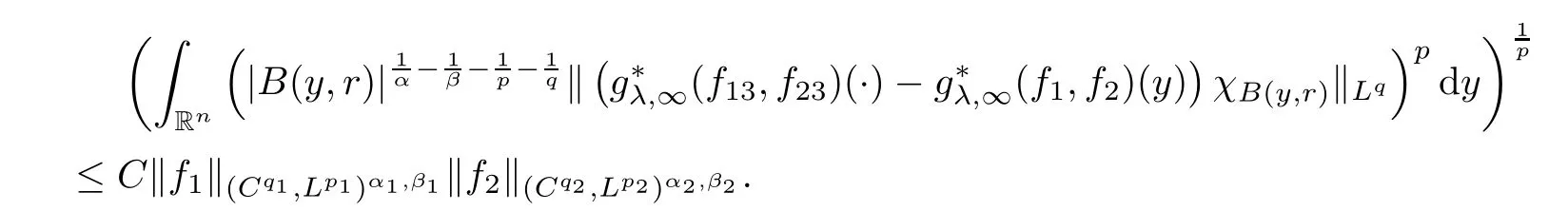

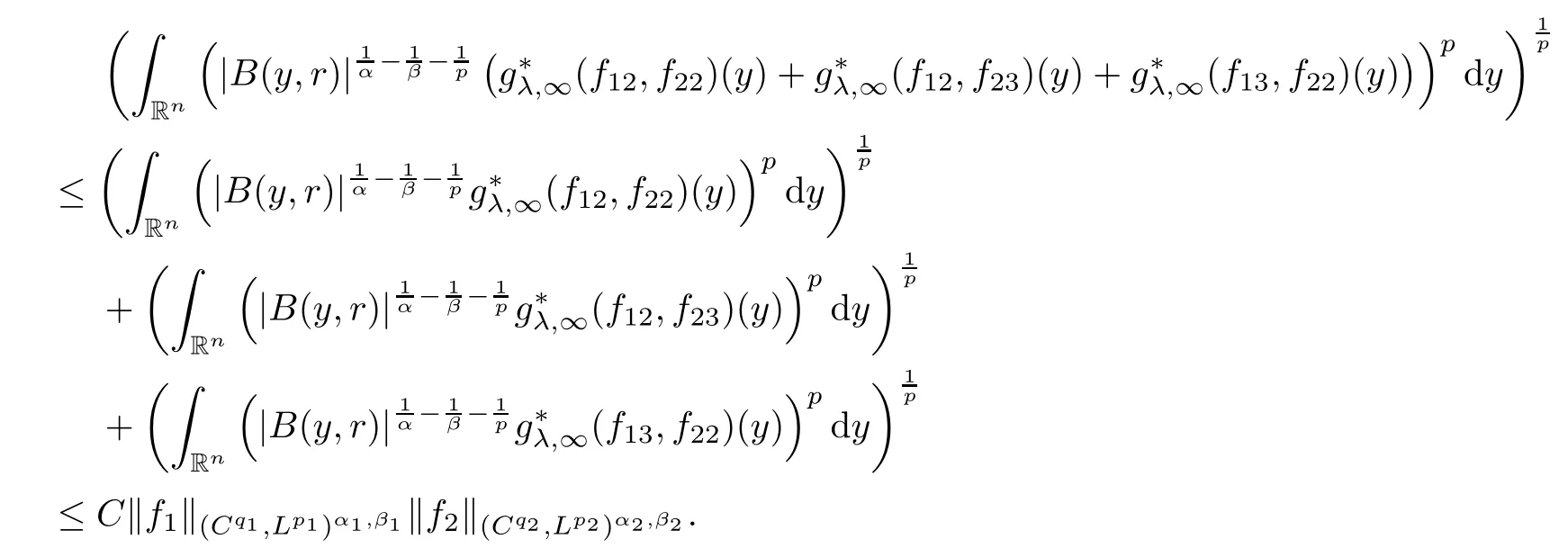
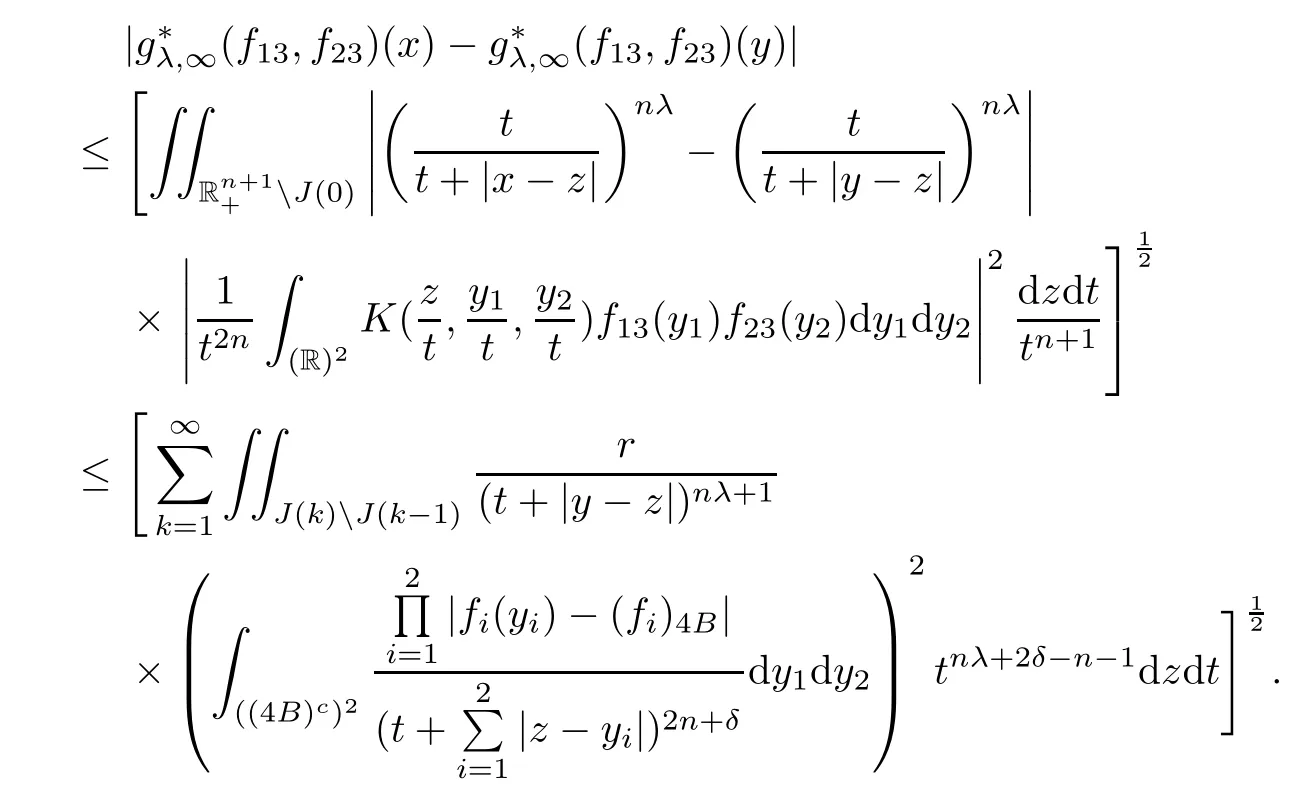
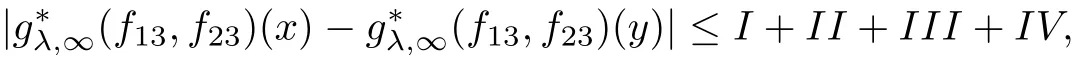

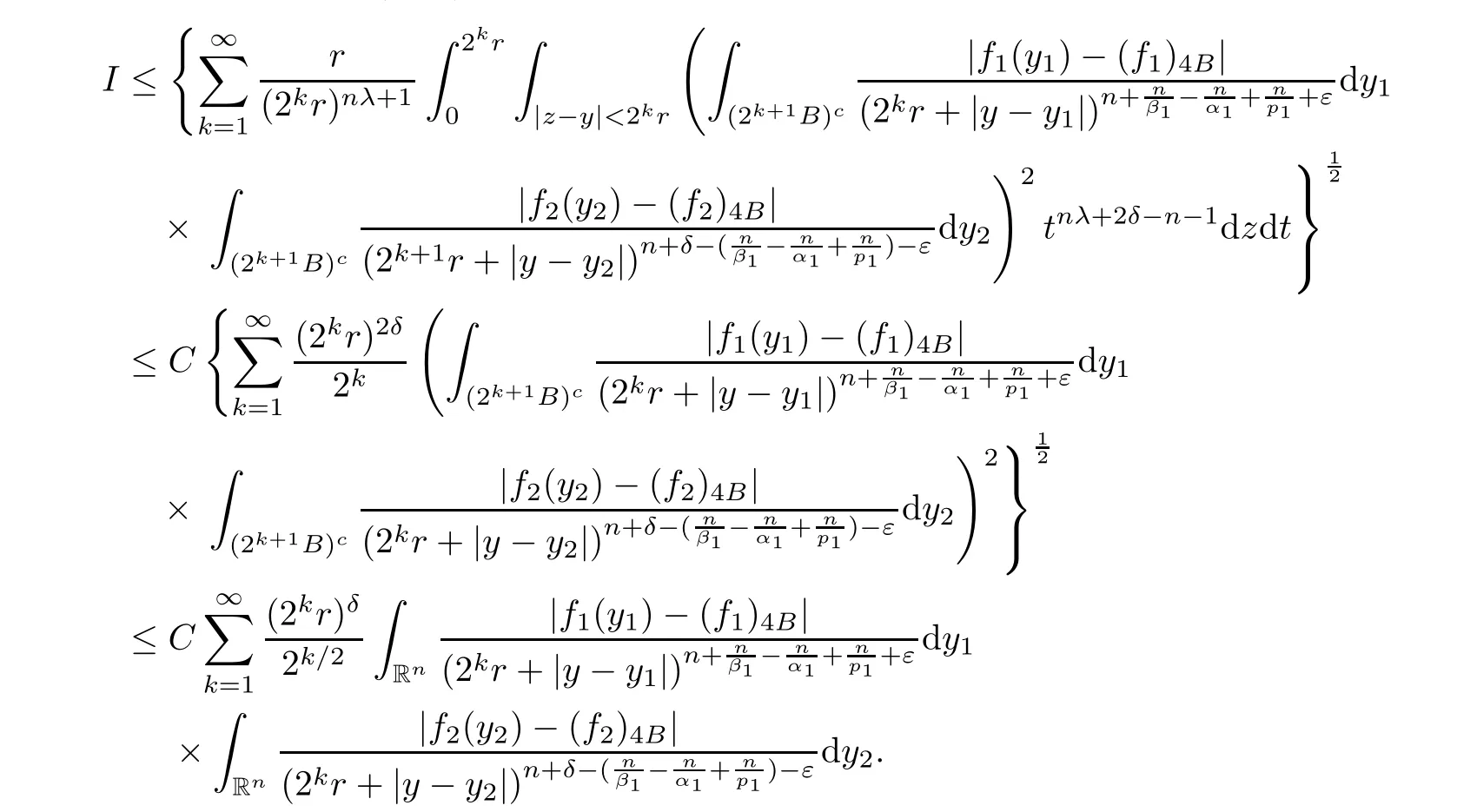
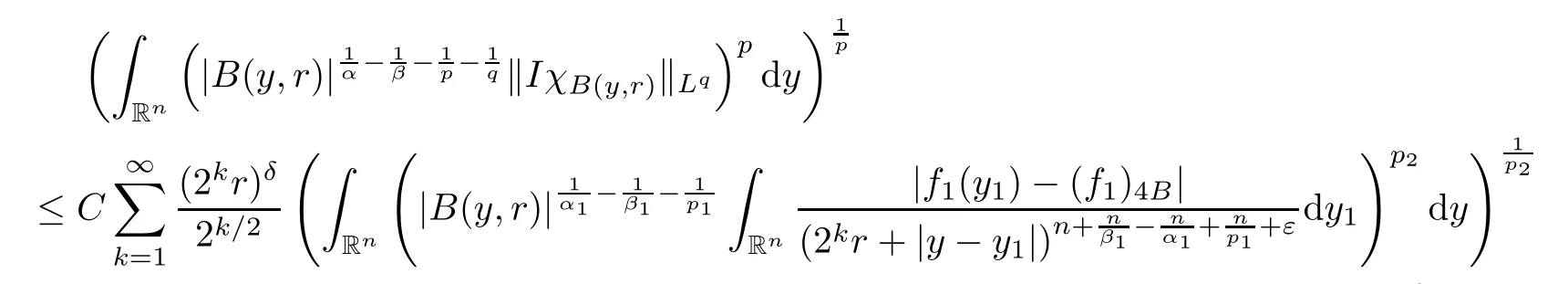
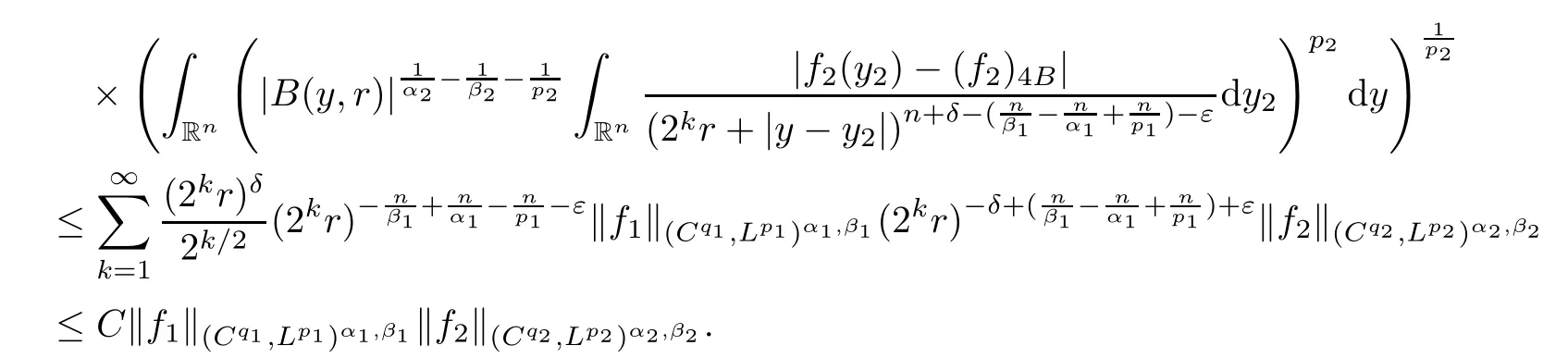
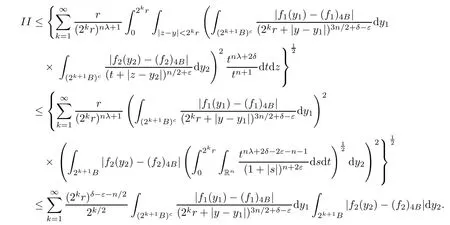


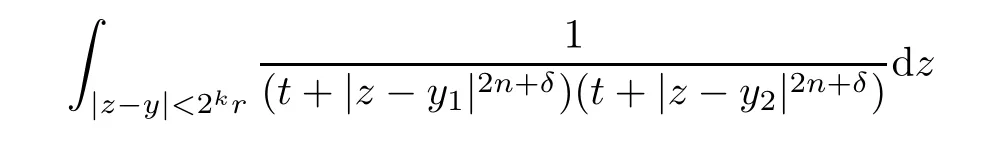


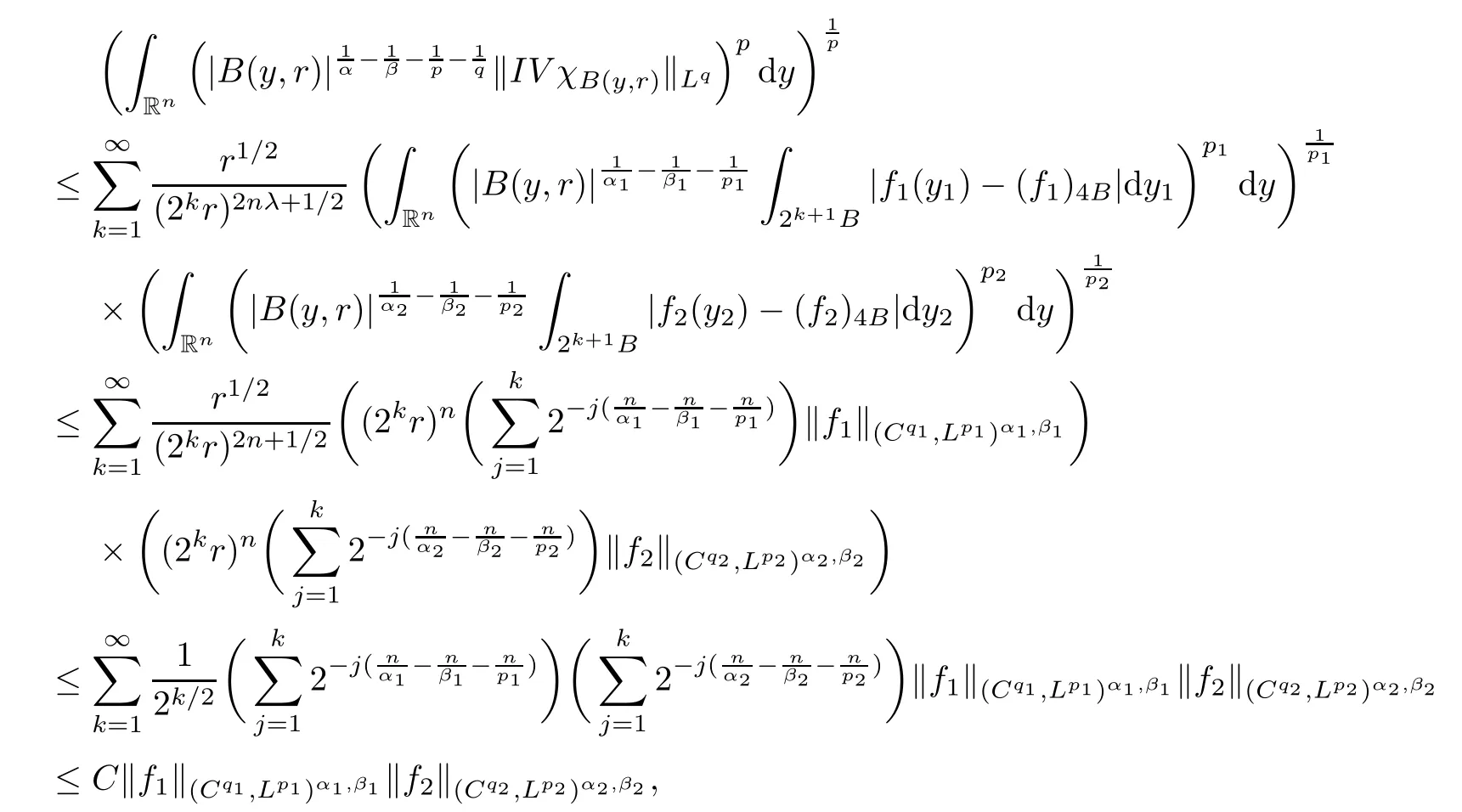
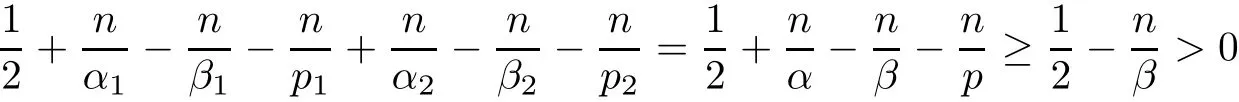
3 Proof of Theorem 1.4
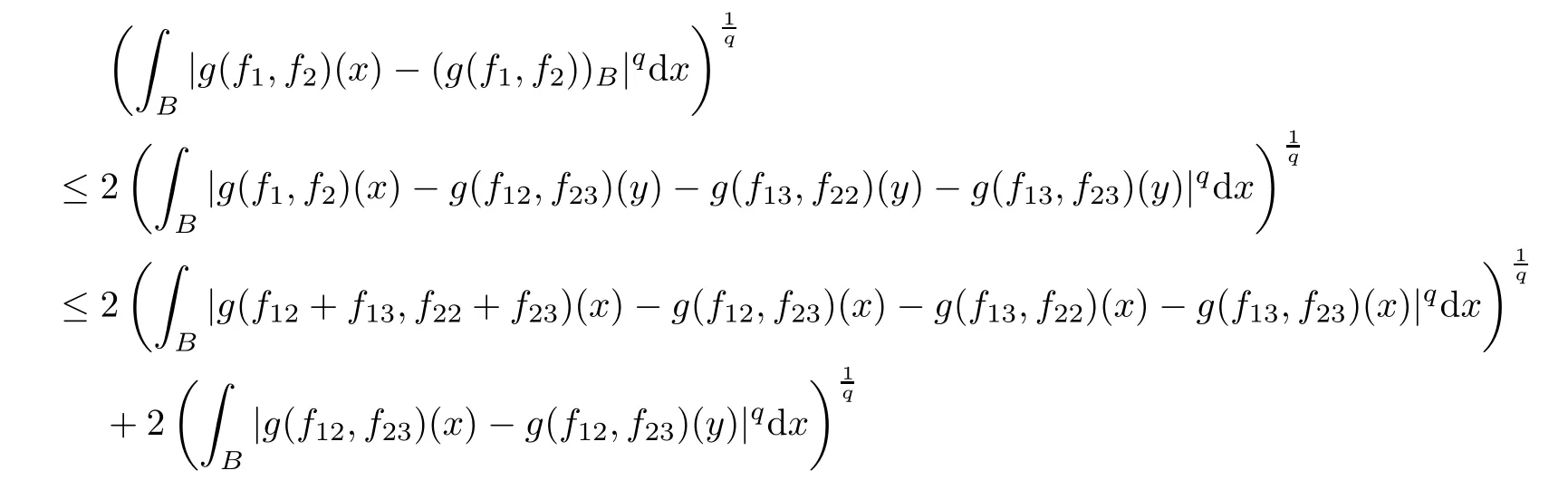
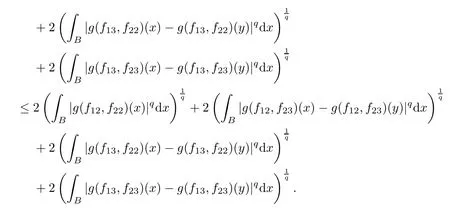
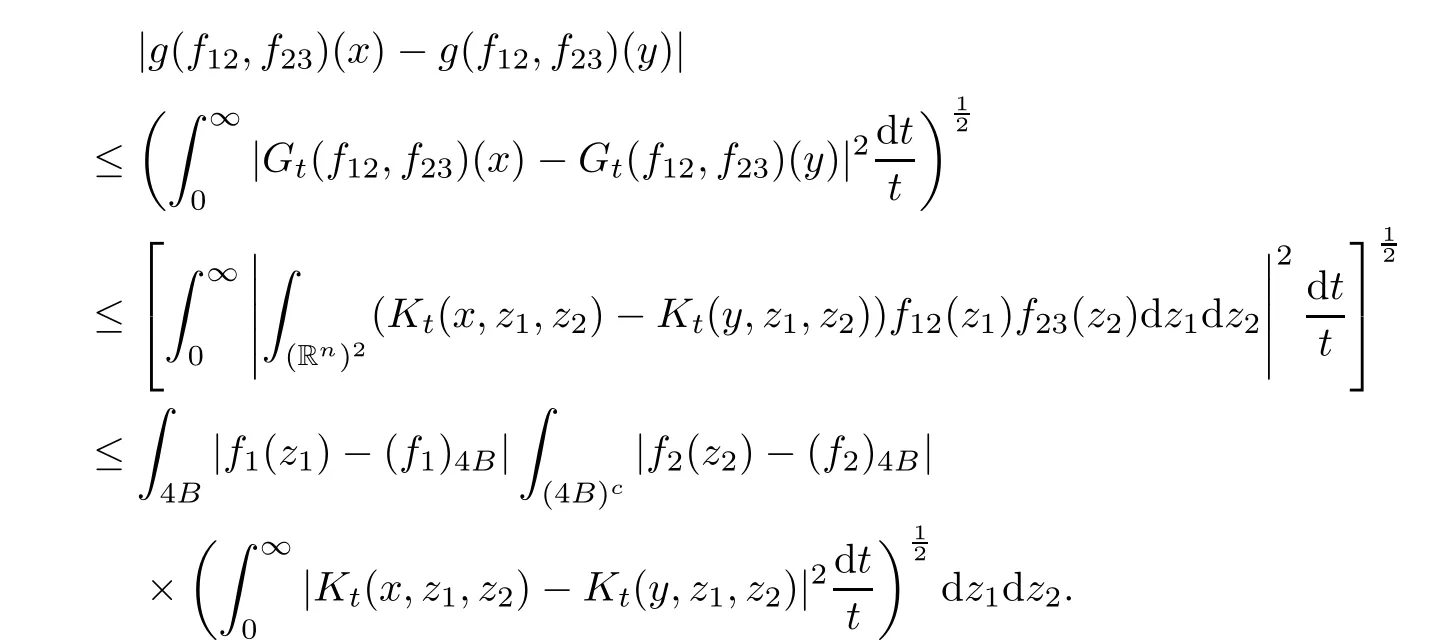
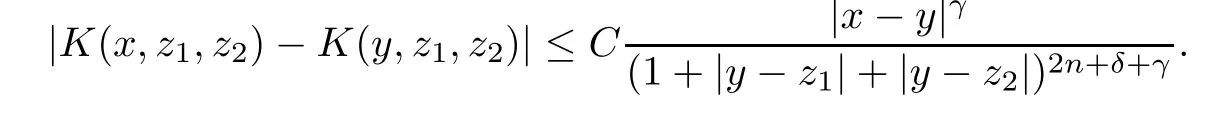
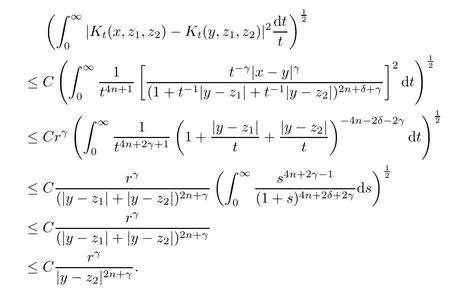
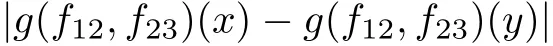
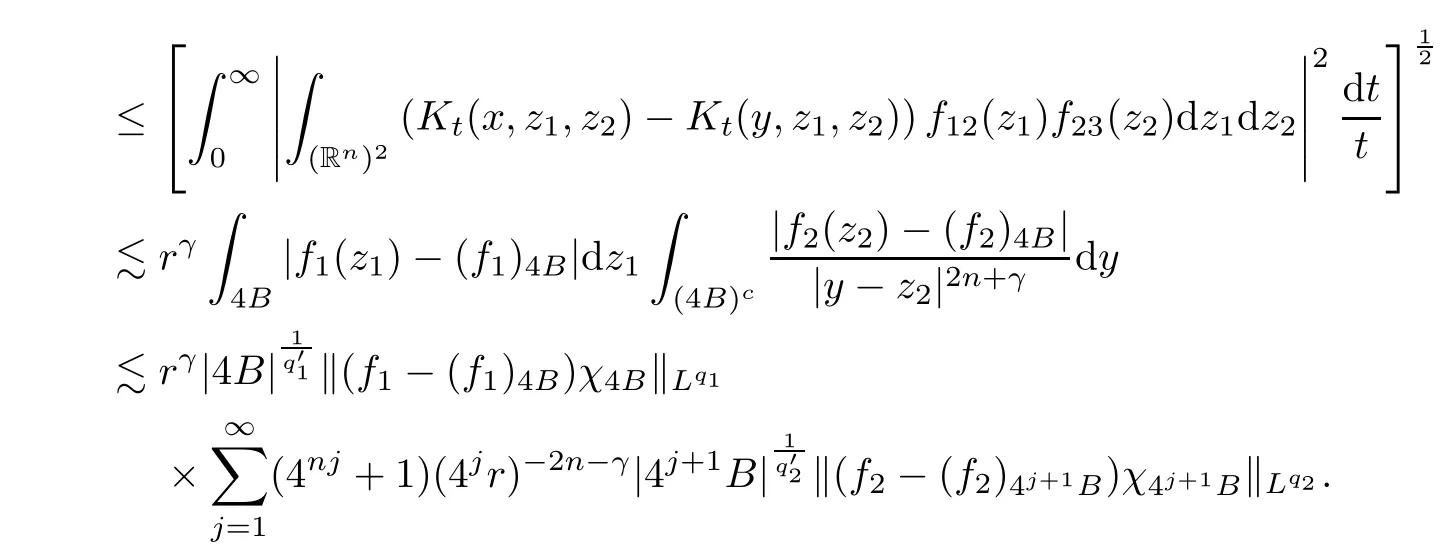
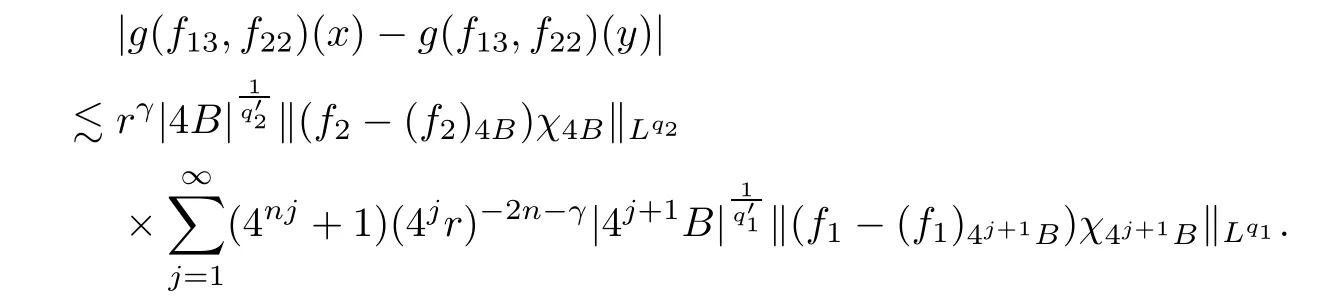
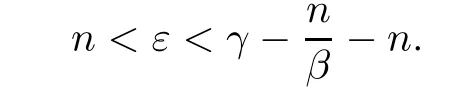

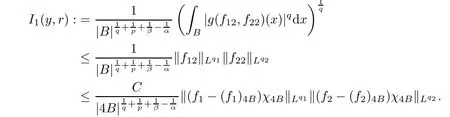
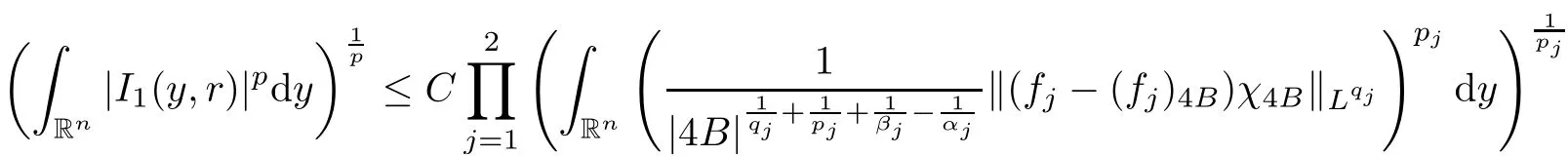
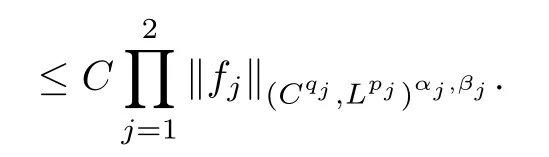
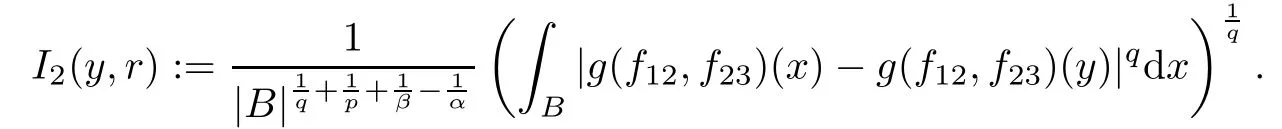
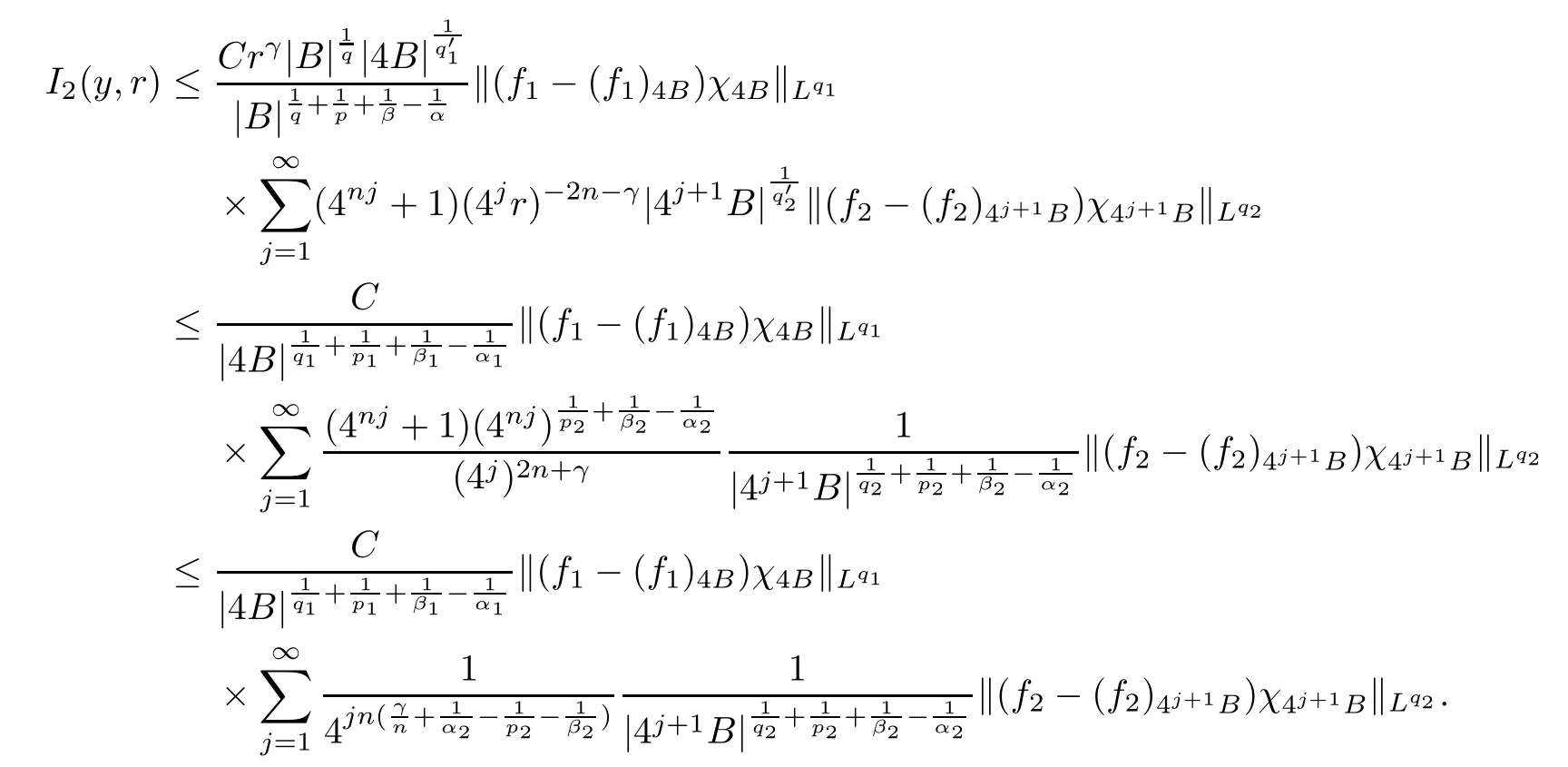
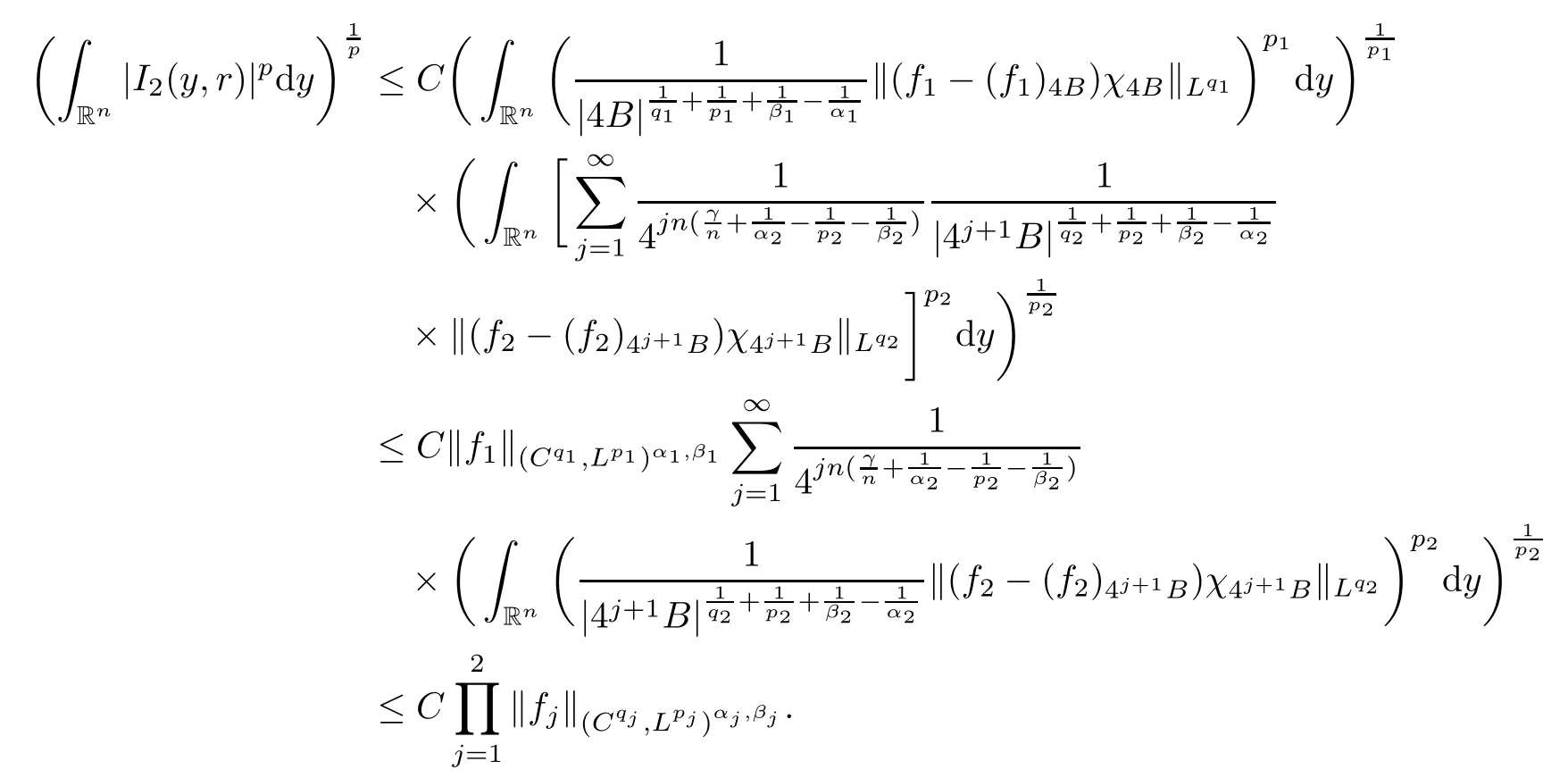
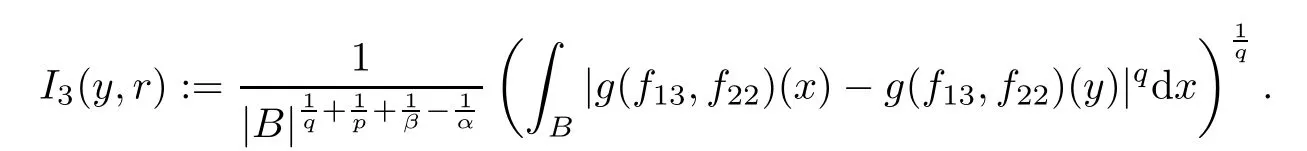
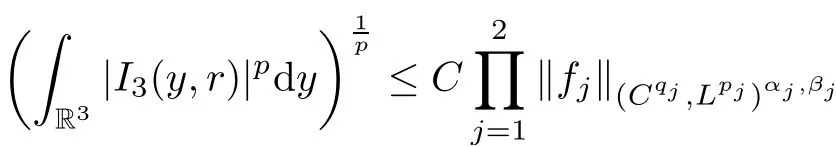


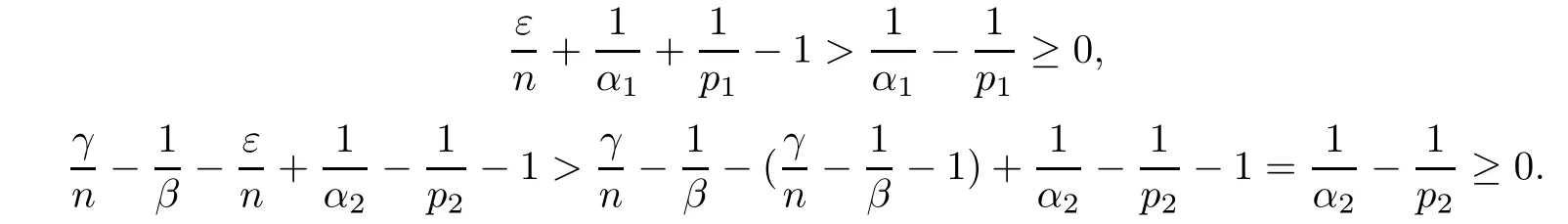
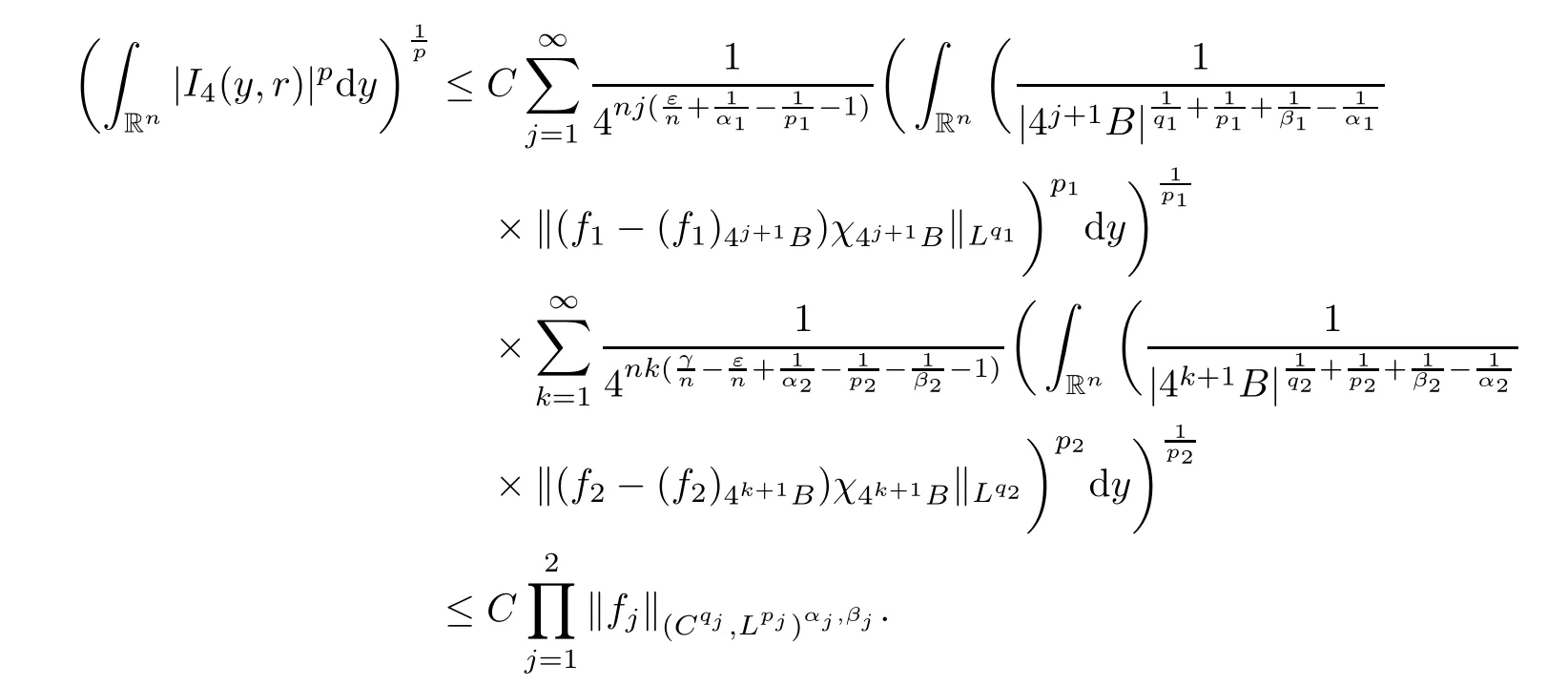
4 Proof of Theorem 1.5
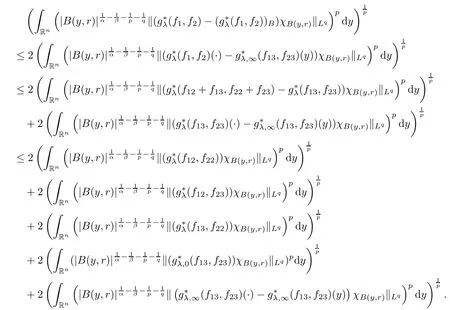

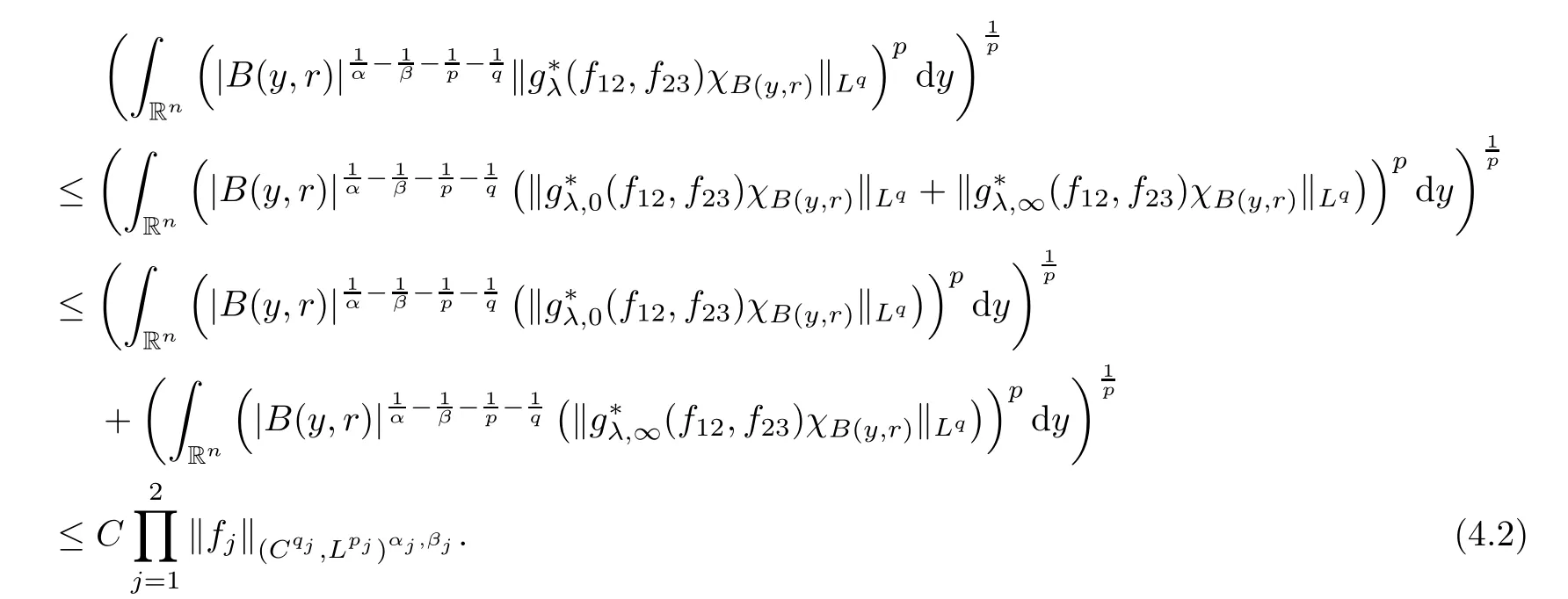
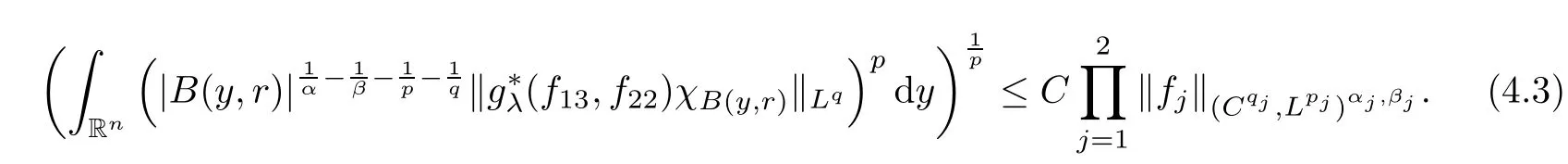
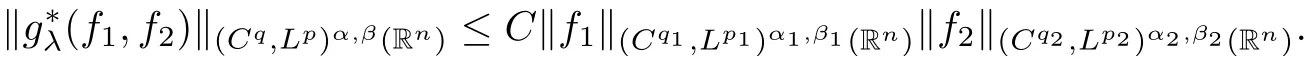
 Acta Mathematica Scientia(English Series)2020年1期
Acta Mathematica Scientia(English Series)2020年1期
