丟番圖方程x3±53=6qy2的整數(shù)解

杜先存, 梁開(kāi)元, 王 鳳

(紅河學(xué)院 教師教育學(xué)院, 云南 蒙自 661199)

方程x3±a3=Dy2(a∈Z+,D是無(wú)平方因子的正整數(shù))是一類重要的丟番圖方程,其整數(shù)解受到越來(lái)越多的學(xué)者的關(guān)注,a=1時(shí)結(jié)論比較多[1-3].a=5時(shí)已有部分結(jié)論,當(dāng)D不含6k+1形素因子的情況已基本解決.D含1個(gè)6k+1形素因子的情況僅有部分結(jié)論,主要為:當(dāng)D僅含一個(gè)6k+1形素因子時(shí)結(jié)論見(jiàn)文獻(xiàn)[4-5];當(dāng)D含素因子2,且含一個(gè)6k+1形素因子時(shí)結(jié)論見(jiàn)文獻(xiàn)[6-7];當(dāng)D含素因子3,且含一個(gè)6k+1形素因子時(shí)結(jié)論見(jiàn)文獻(xiàn)[8-11].當(dāng)D同時(shí)含素因子2及3,且含一個(gè)6k+1形素因子時(shí),目前還沒(méi)有相關(guān)結(jié)論,本文研究了此情況.

1 相關(guān)引理

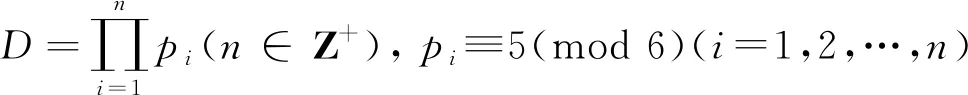
ⅰ)q=27t2+1(t∈N) ;

ⅱ)q=12t2+1(t∈N);

ⅲ)q=3(3t+1)(3t+2)+1(t∈N).

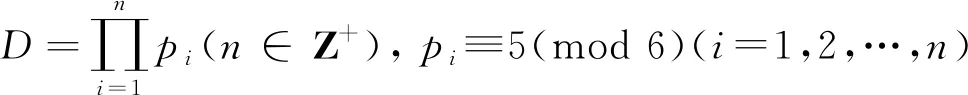
ⅰ)q=27t2+1(t∈N);

ⅱ)q=12t2+1(t∈N);

ⅲ)q=3(3t+1)(3t+2)+1(t∈N).

2 定 理

定理1 設(shè)q≡1(mod 6)為奇素?cái)?shù),則丟番圖方程

x3+53=6qy2,

(1)

在滿足下列條件時(shí),僅有整數(shù)解(x,y)=(-5,0):

ⅰ)q=27t2+1,t≡0,2,3(mod 5);

ⅱ)q=12t2+1,t≡0,2,3(mod 5);

ⅲ)q=3(3t+1)(3t+2)+1(t∈N),t≡1,2,3(mod 5).

定理2 設(shè)q≡1(mod 6)為奇素?cái)?shù),則丟番圖方程

x3-53=6qy2,

(2)

在滿足下列條件時(shí),僅有整數(shù)解(x,y)=(5,0):

ⅰ)q=27t2+1,t≡0,2,3(mod 5);

ⅱ)q=12t2+1,t≡0,2,3(mod 5);

ⅲ)q=3(3t+1)(3t+2)+1(t∈N),t≡1,2,3(mod 5).

3 定理證明

當(dāng)x?0(mod 5)時(shí),因?yàn)間cd(x+5,x2-5x+25)=1或3,而x2-5x+25?0(mod 2),則方程(1)可分解為以下8式:

情形Ⅰx+5=6qu2,x2-5x+25=v2,y=uv,gcd(u,v)=1;

情形Ⅱx+5=6u2,x2-5x+25=qv2,y=uv,gcd(u,v)=1;

情形Ⅲx+5=2qu2,x2-5x+25=3v2,y=uv,gcd(u,v)=1;

情形Ⅳx+5=2u2,x2-5x+25=3qv2,y=uv,gcd(u,v)=1;

情形Ⅴx+5=18qu2,x2-5x+25=3v2,y=3uv,gcd(u,v)=1;

情形Ⅵx+5=18u2,x2-5x+25=3qv2,y=3uv,gcd(u,v)=1;

情形Ⅶx+5=6qu2,x2-5x+25=9v2,y=3uv,gcd(u,v)=1;

情形Ⅷx+5=6u2,x2-5x+25=9qv2,y=3uv,gcd(u,v)=1.

以下分別討論這8種情形下方程(1)的解的情況.

情形Ⅰ 由x2-5x+25=v2得x=-16,-3,0,5,8,21,則6qu2=-21,-8,-5,0,3,16,顯然無(wú)解,故情形Ⅰ不成立.

情形Ⅱ 由x2-5x+25=qv2配方得(2x-5)2+75=4qv2,把x=6u2-5代入可得9(4u2-5)2+75=4qv2,兩邊取模3,得由qv2≡0(mod 3).又q=27t2+1(t∈N)或q=12t2+1(t∈N)或q=3(3t+1)(3t+2)+1(t∈N),則有q≡0(mod 3),因此有v≡0(mod 3),則由x2-5x+25=qv2得x2-5x+25≡0(mod 3),即有g(shù)cd(x+5,x2-5x+25)=3,這與gcd(x+5,x2-5x+25)=1矛盾,故情形Ⅱ不成立.

情形Ⅳ 由x2-5x+25=3qv2配方得(2x-5)2+75=12qv2,兩邊取模5得

(2x-5)2+75≡12qv2(mod 5).

(3)

因?yàn)?

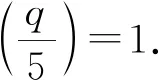
仿情形Ⅲ的證明可知情形Ⅴ不成立.

仿情形Ⅳ的證明可得情形Ⅵ不成立.

情形Ⅶ 由x2-5x+25=9v2配方有(2x-5)2+75=36v2,把x+5=6qu2代入得(12qu2-15)2+75=36v2,兩邊取模9,得3≡0(mod 9),矛盾,故情形Ⅶ不成立.

仿情形Ⅶ的證明可知情形Ⅷ也不成立.

綜上所述,Diophantine方程(1)在題設(shè)條件下僅有整數(shù)解(x,y)=(-5,0),定理1得證.

根據(jù)引理2,仿定理1的證明可知定理2成立.

4 結(jié) 論

本文通過(guò)利用初等方法得出了q≡1(mod 6)為奇素?cái)?shù)時(shí),丟番圖方程x3±53=6qy2當(dāng)q=27t2+1,t≡0,2,3(mod 5)或q=12t2+1,t≡0,2,3(mod 5)或q=3(3t+1)(3t+2)+1,t≡1,2,3(mod 5)時(shí)的整數(shù)解的情況,此結(jié)果對(duì)于該類丟番圖方程的求解起了一定的借鑒作用,同時(shí)推進(jìn)了該類丟番圖方程的研究.