WU Yingdong,WU Shaohua,CHENG Xin and LIU Lei

School of Mathematics and Statistics,Wuhan University,Wuhan 430072,China.

Abstract. In this paper,we discuss the local existence of weak solutions for a parabolic system modelling chemotaxis with memory term, and we show the finite-time blowup and chemotactic collapse for this system. The main methods we used are the fixed point theorem and the semigroup theory.

Key Words: parabolic system;chemotaxis;memory term;fixed point theorem;blow-up.

1 Introduction

In this paper,we consider the following model:

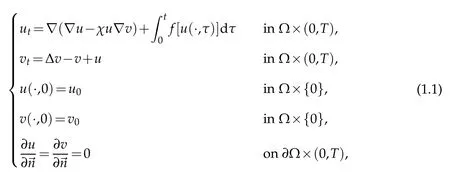
where ??RN, a bounded open domain with smooth boundary??,is the unit outer normal on?? andχis a nonnegative constant.Andfis a continuous linear function and it satisfies the condition:whereLis a positive constant.

Our model is initiated by the PKS model which is a mathematical model of biological phenomena. And this model for chemosensitive movement has been developed by Patlak,Keller and Segel[1].

whereurepresents the population density andvdenotes the density of the external stimulus,χis the sensitive coefficient,the time constantε(0≤ε≤1)indicates that the spatial spread of the organismsuand the signalvare on different time scales. The caseε=0 corresponds to a quasi-steady state assumption for the signal distribution.

Since the PKS model is designed to describe the behavior of bacteria and bacteria aggregates, the question arises whether or not this model is able to show aggregation.Plenty of theoretical research uncovered exact conditions for aggregations and for blow up(see,e.g.,Childress and Percus[2,3], J¨ager and Luckhaus[4], Nagai[5], Gajewski et al.[6],Senba[7],Rasde and Ziti[8],Herrera and Velasquez[9],Othmer and Stevens[10]or Levine and Sleeman[11]).

Global existence below these thresholds has been proven using a Lyapunov functional in Gajewski, et al. [6], Nagai, et al. [12] and Biler [13]. Besides, a number of theoretical research found exact conditions for aggregations and other properties[14–16]. Free boundary problems for the chemotaxis model are considered[17–20].

Our study of (1.1) is also motivated by the following problem for the heat equation with a general time integral boundary condition[21]:

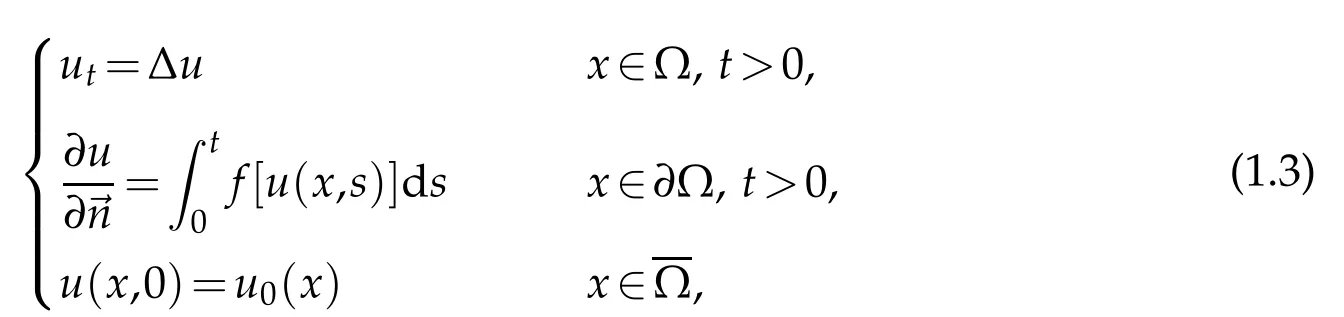
where ? is a bounded domain in RNwith boundary???C1+μ(0<μ<1),is the outward normal,andu0(x)is a nonnegative function such that

fis a nondecreasing function withf∈C1(0,∞)andf(0)>0.

Considering the nonlinear time integral condition governing flux through the boundary,the model(1.1)involves a continuous time delay which is often referred to as a memory condition in the literature. This memory term can perfectly describe the movement of population density or the movement of single particles. Especially,the movement behavior of most species is guided by external signals: insects orient towards light sources,the smell of a sexual partner makes it favorable to choose a certain direction.

Models with memory terms present in the boundary flux have been formulated in many applied sciences. For example, in [22], a linear memory boundary condition is introduced for the study of thermodynamics. It takes into account the hereditary effects on the boundary as those studied in [23,24]. Similar hereditary boundary conditions have been employed in models of time-dependent electromagnetic fields at dissipative boundaries[25].

From the mathematical point of view, it is significant to study the local existence of weak solution for chemotaxis system with memory terms and the finite-time blow-up for this system.In our previous work,we have done something for this[26].

2 Some basic lemmas

Choose a constantσwhich satisfies

and

It is easy to check that (2.1) and (2.2) can be simultaneously satisfied in the case of 1≤N≤3.We define

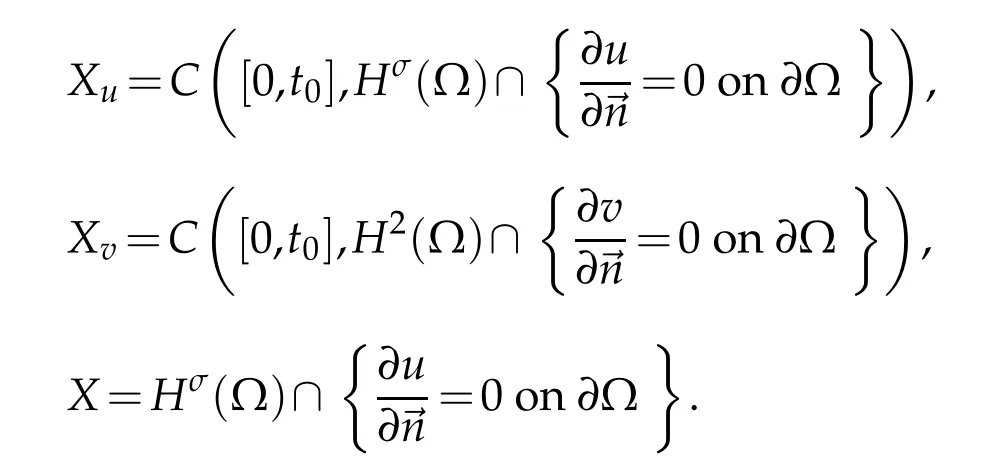
Here,means that0 on??}for eacht∈[0,t0]and. In the Sections 2 and 3,inessential constants will be denoted by the same letterc,even if they may vary from line to line.

Lemma 2.1.Let p(z)be a holomorphic semigroup on a Banach space Y,with generator A.Then

and

Proof.The proof can be found in[27,Proposition 7.2].

If ? is a bounded open domain with smooth boundary, on which the Neumann boundary condition is placed, then we know thatet?defines a holomorphic semigroup on the Hilbert spaceL2(?). So by Lemma 2.1,we have that

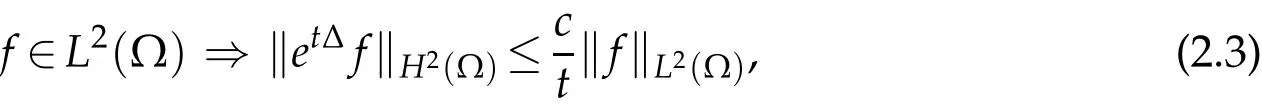
where

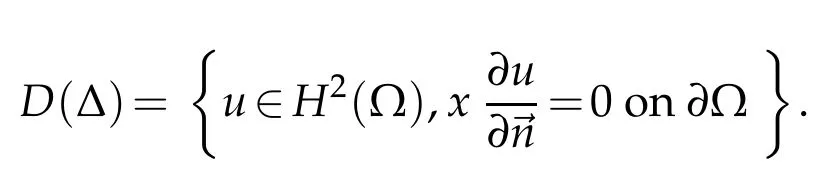
Applying interpolation to(2.3)yields

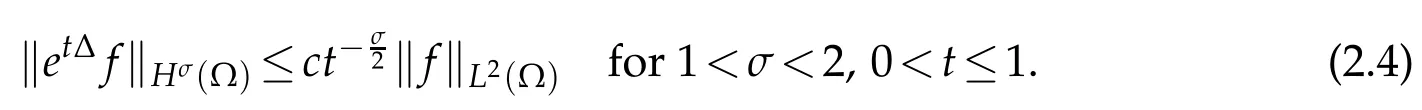
Lemma 2.2.We assume that u∈X,a Banach space of functions,and that there is another Banach space Y such that the following four conditions hold:

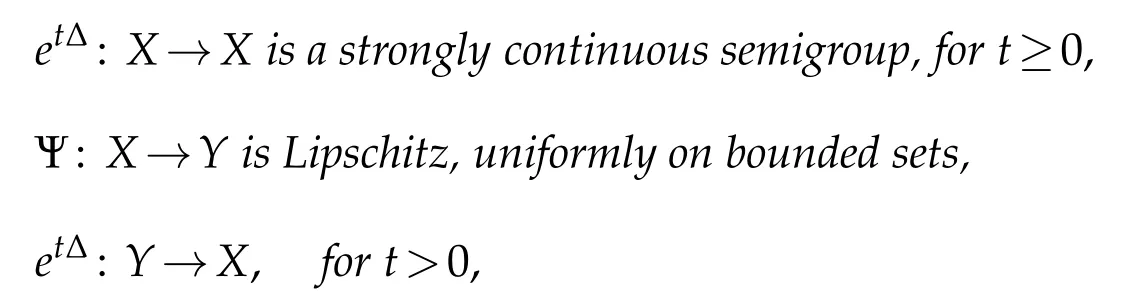
and,for some γ<1,

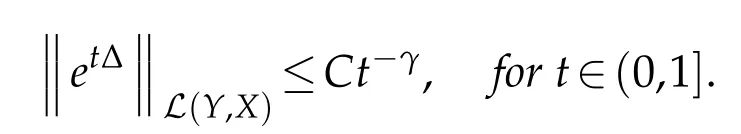
Then we have a bound

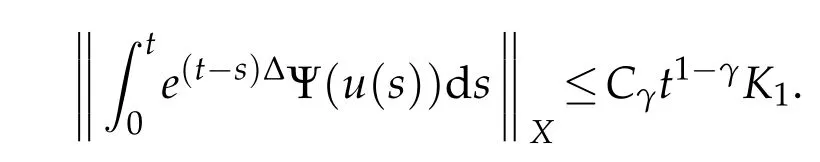
Proof.The proof can be found in[27].

Dividing system(1.1)into two parts:

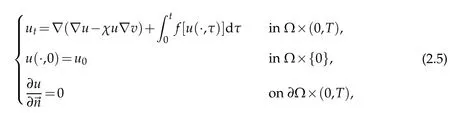
and

then we have the following lemmas.

Lemma 2.3.For,t0>0small enough,problem(2.6)hasa unique solution v∈Xv,and v satisfies

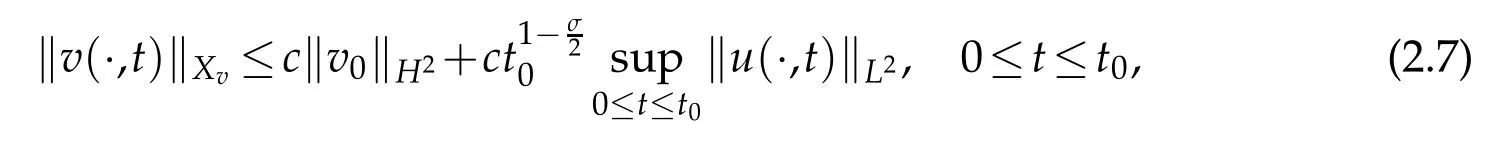
where c is a constant which is independent of T.

Proof.It is obvious that Eq. (2.6) has a solution and the solution is unique. So what we need to proof is(2.7). LetT(t)=et?,where,then

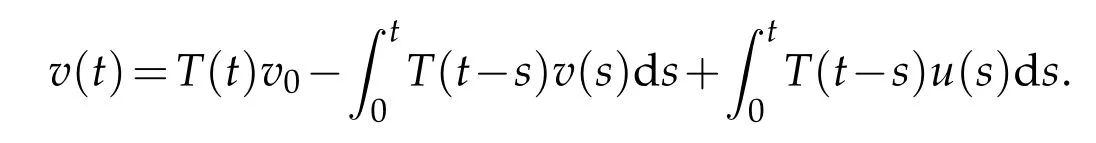
By(2.3),Lemma 2.2,we calculate

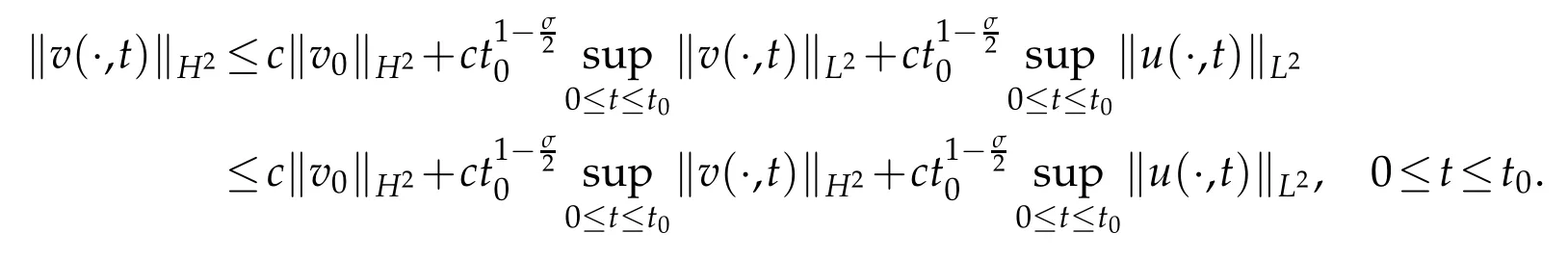
Thus for small enought0,(2.7)holds.

Lemma 2.4.For each u0∈Hσ(?)and v∈Xv,σ and N satisfy(2.1)and(2.2). The problem(2.5)has a unique solution u∈c([0,t0],Hσ(?)),and the solution can be written as

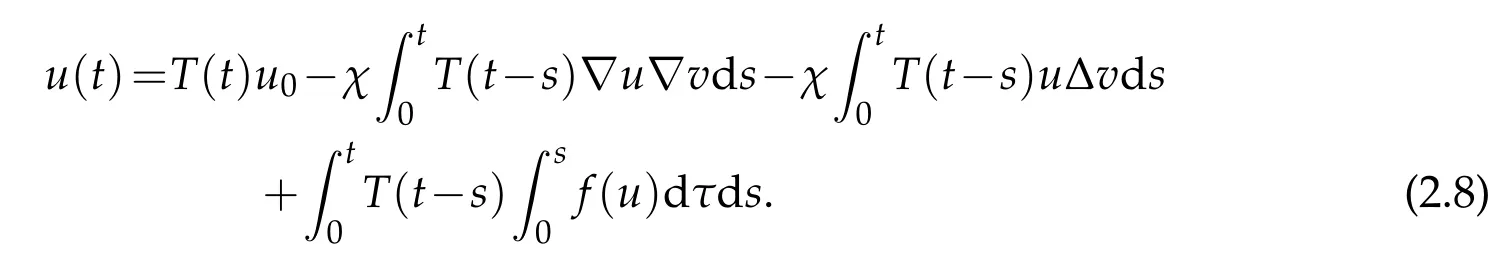
Proof.We consider the following problem first

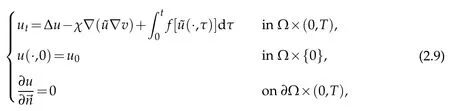
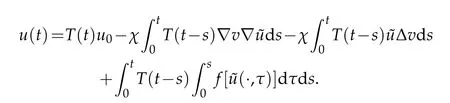
Define a mapping

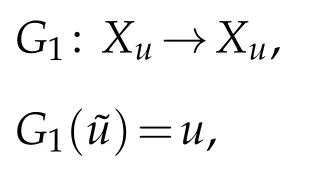
whereuis the corresponding solution of(2.9).

Then we claim that fort0small enough,G1is a contract mapping.In fact,letwe have

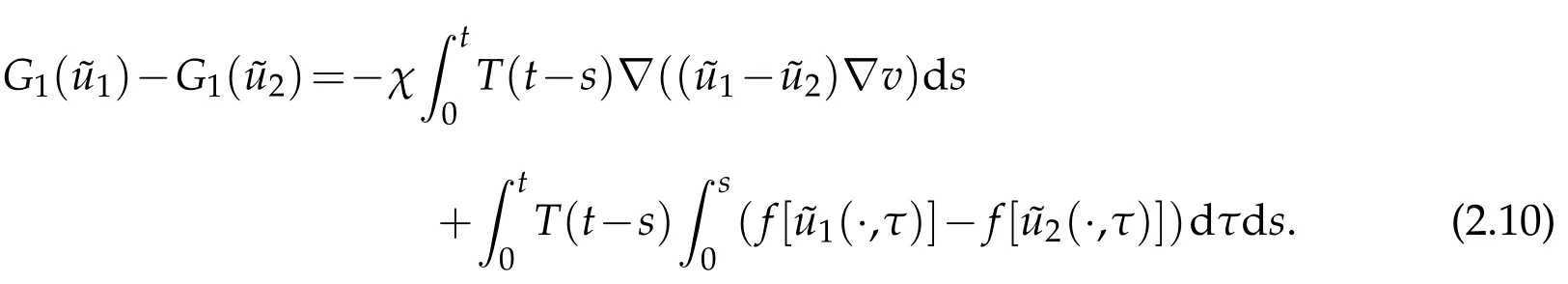
By Sobolev imbedding theorems,we have

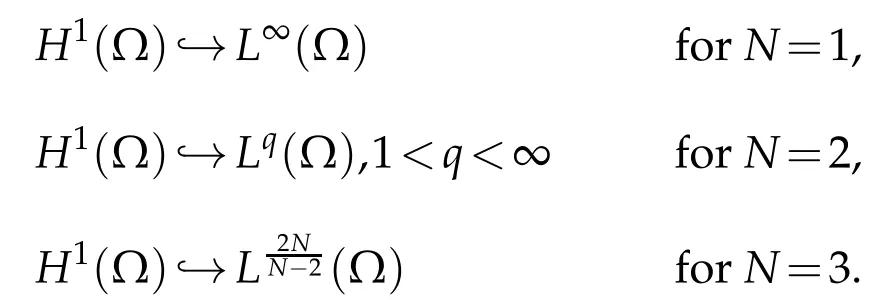
IfN=1,

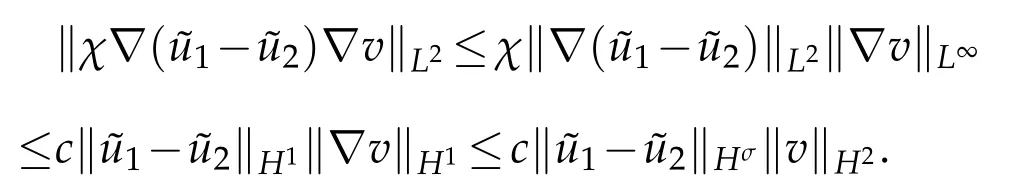
IfN=2,3,according to(2.1)and(2.2),we obtain that

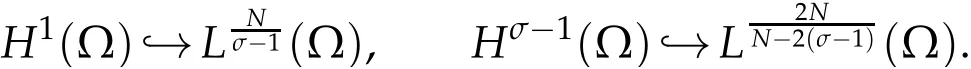
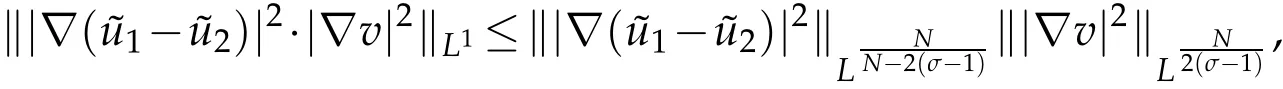
which implies

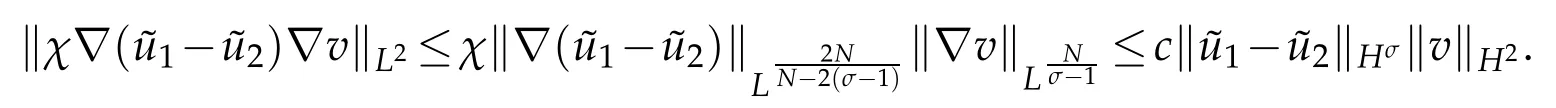
Hence forN=1,2,3,we have

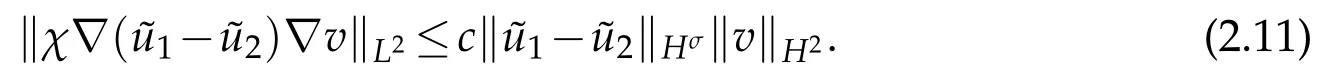
Similarly,we have

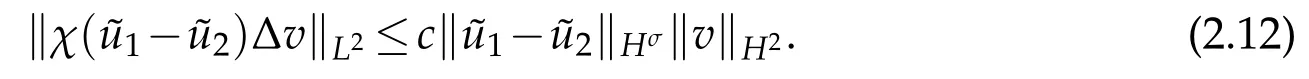
So for the first term on the right side of(2.10),N=1,2,3,by(2.11)and(2.12),we have

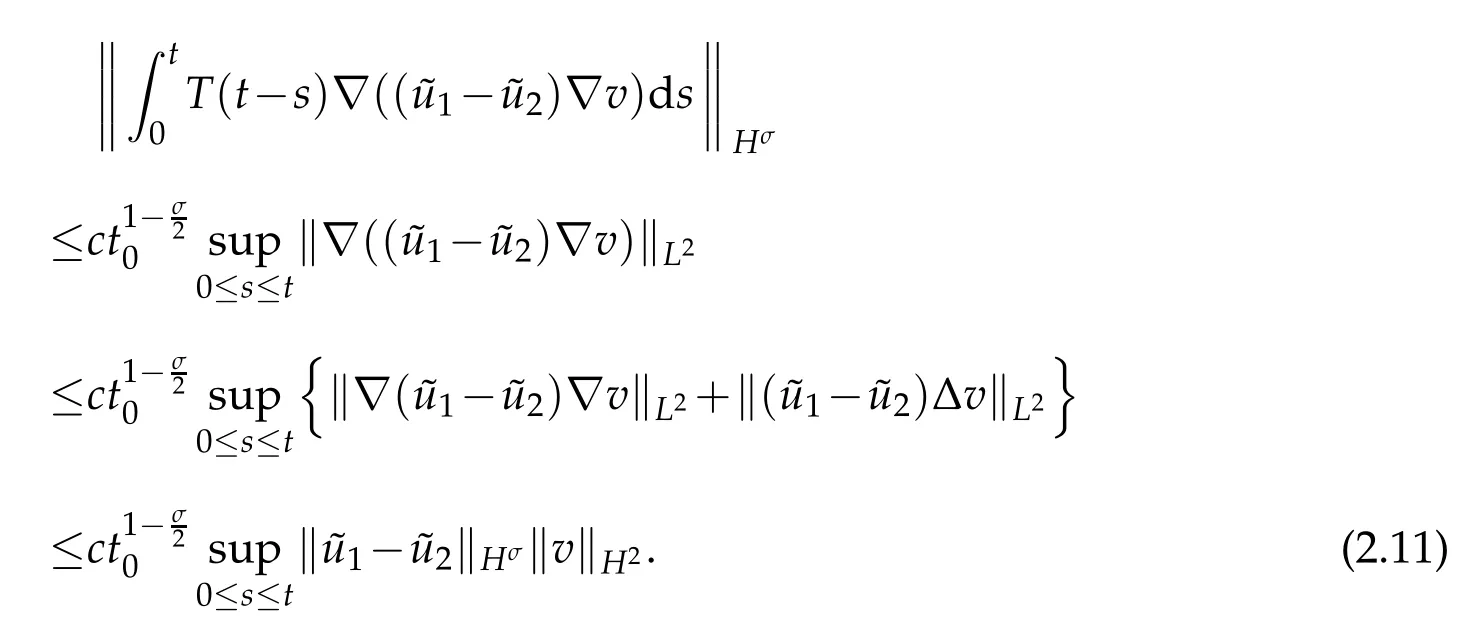
For the second term on the right side of(2.10),we have

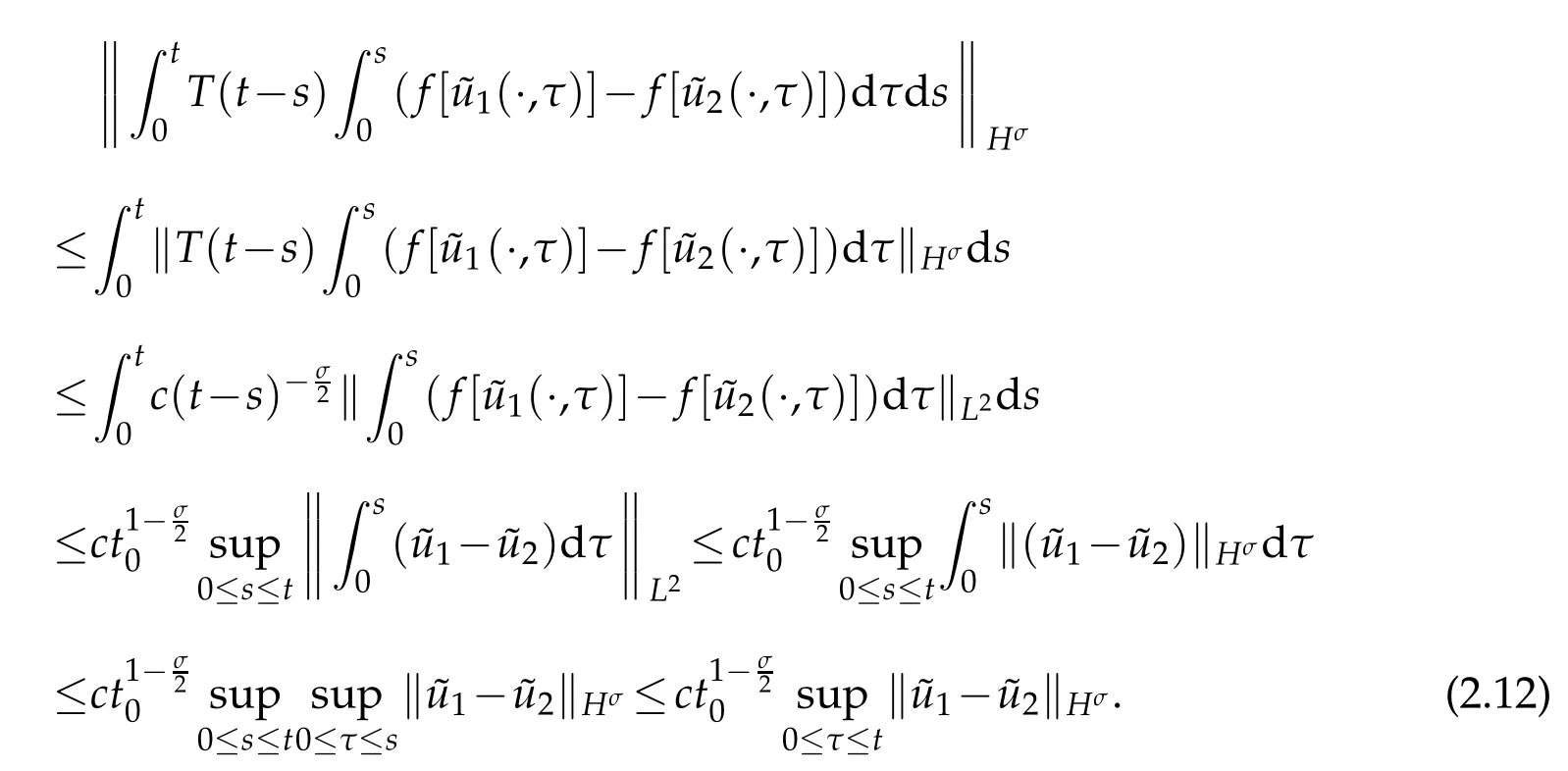
So we have

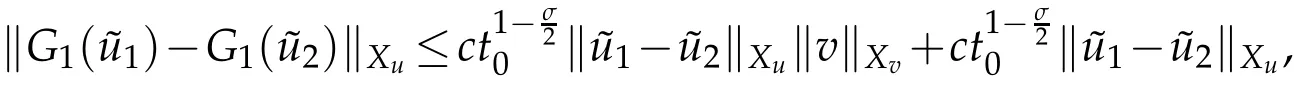
which implies fort0>0 small enough,G1is contract. By Banach fixed point theorem,there exists a unique fixed point ?usuch that. Then we have the local solution of the problem(2.5):

This completes the proof of the lemma.

Lemma 2.5.Assume σ,N as given by(2.1)and(2.2). For solution u∈Xu of(2.5),we have

Proof.By Lemma 2.3,(2.5)has a unique solution,and the solution can be written as

Next we prove estimate(2.13). By(2.4)we have

By Sobolev imbedding theorem,forN=1,we have

ForN=2,3,we have

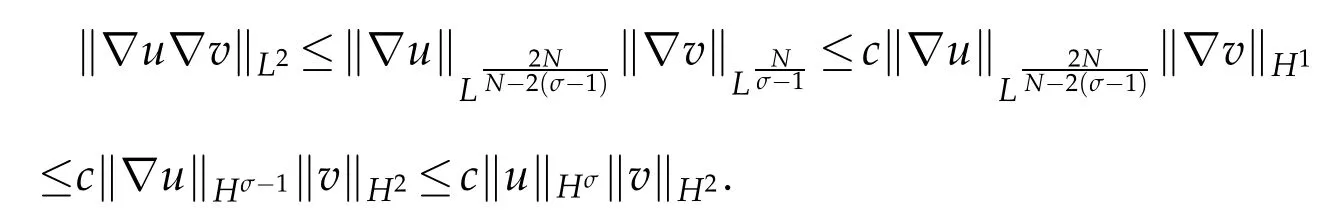
So we obtain that,for 0≤t≤t0,

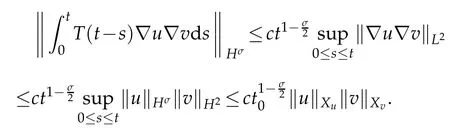
Meanwhile,we deduce

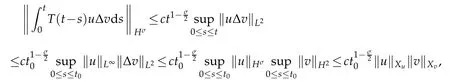
and

Hence we declare that

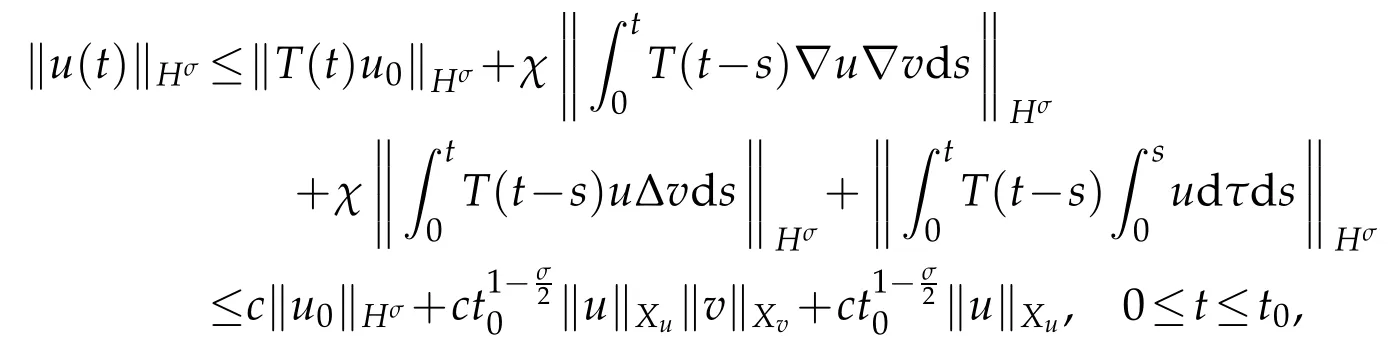
which implies fort0small enough

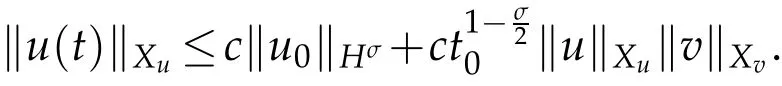
Thus,Lemma 2.5 is proved.

3 Local existence of solution

In this section,we establish the local solution of system(1.1).

Theorem 3.1.Under conditions(2.1)and(2.2),for each initial data0 on??},problem(1.1)has a unique solution(u,v)∈Xu×Xv for some t0>0.

Proof.Considerg∈Xuandg(x,0)=u0(x) and letv=v(g) denotes the corresponding solution of the equation

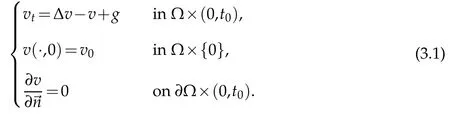
By Lemma 2.2,we havev∈Xvand

For the solutionvof(3.1),defineu=u(v(g))to be the corresponding solution of

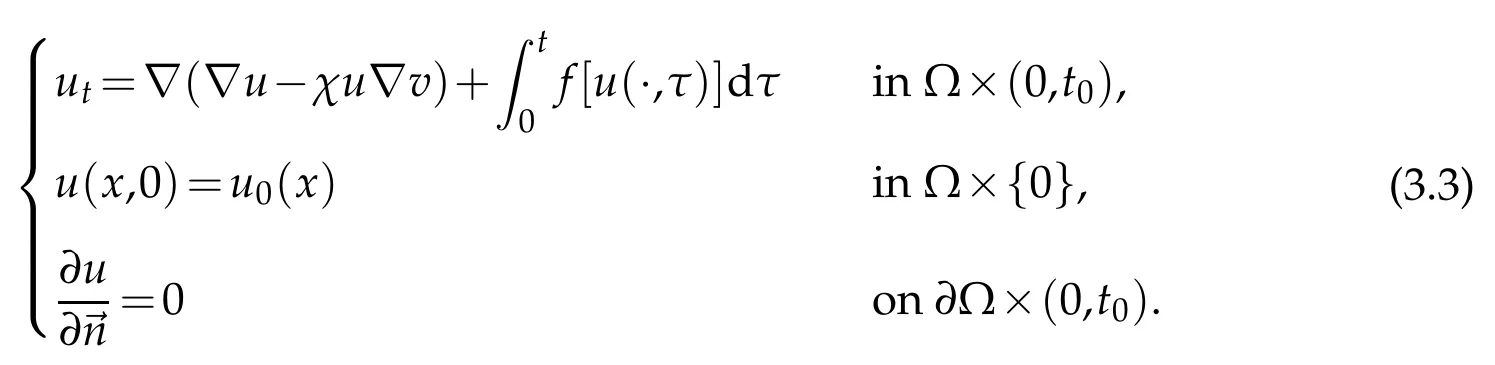
Define a mapping

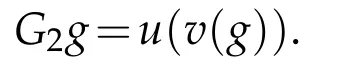
Then Lemma 2.3 shows thatG2:Xu→Xu.Takeand a ball

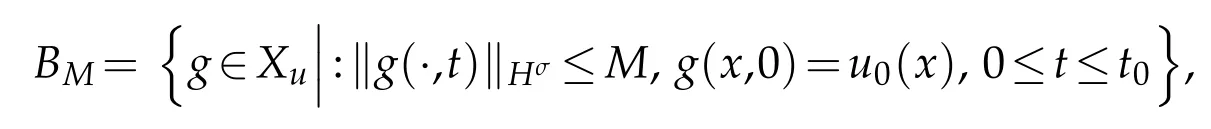
where the constant c is given by(2.13). Then we conclude from(2.13)and(3.2)that

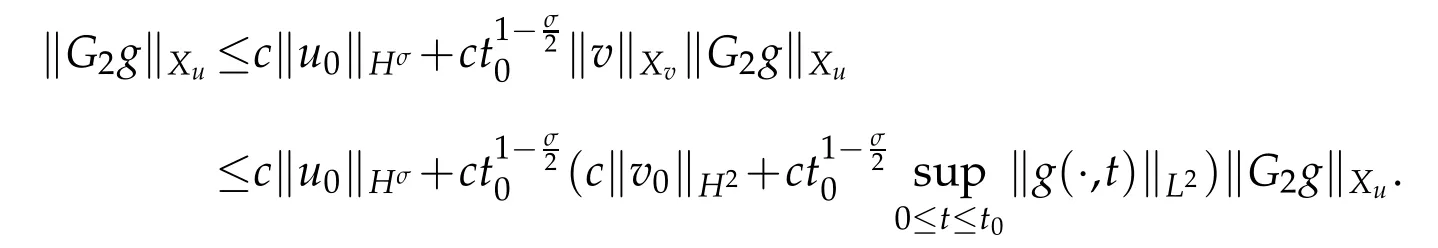
If,then fort0>0 small enoughSo fort0>0 small enough,G2mapsBMintoBM.

Next we demonstrate that fort0small enough,G2is a contract mapping. In fact, letg1,g2∈BM?Xuandv1,v2denote the corresponding solutions of(3.1). Then

For the first term on the right side of(3.4),

where

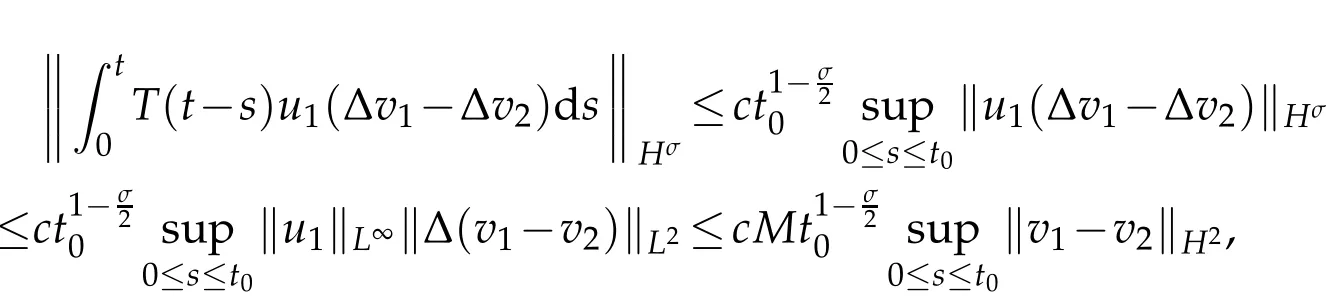
and

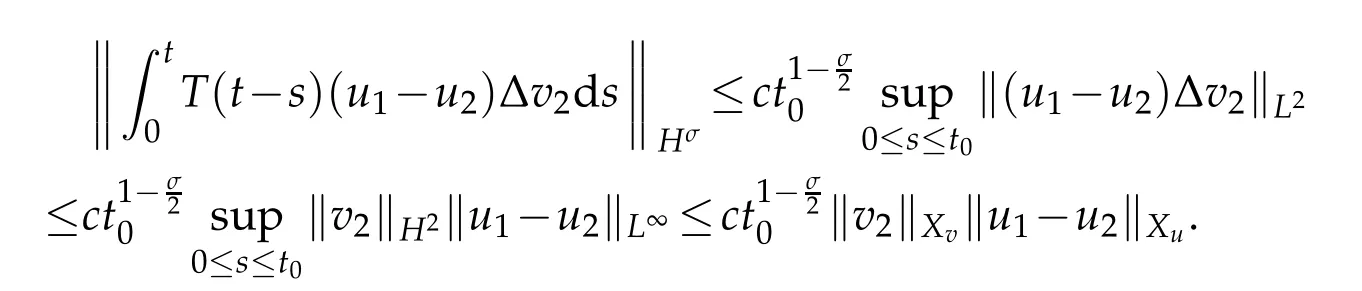
Therefore

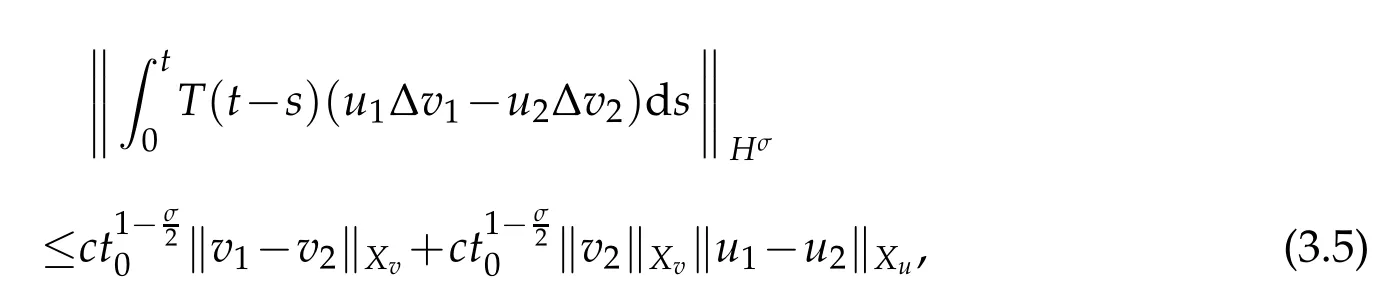
where 0≤t≤t0.For the second term on the right side of(3.4),we have

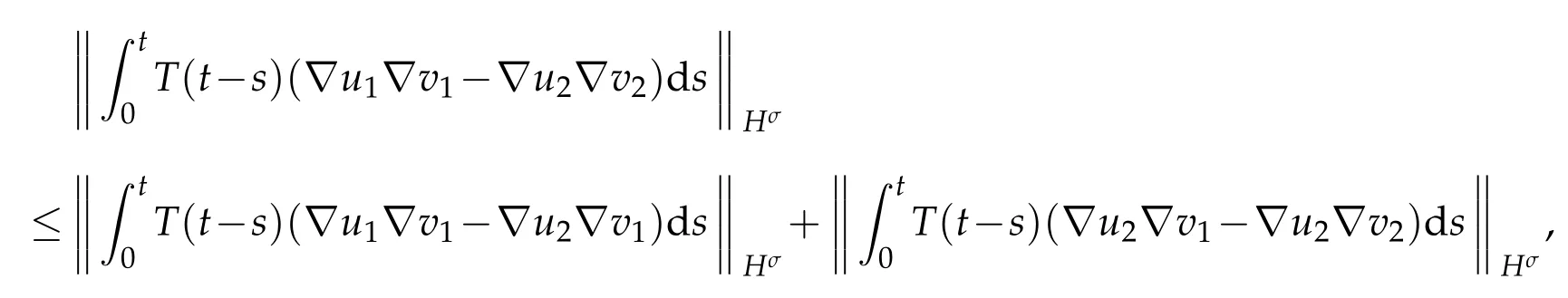
where

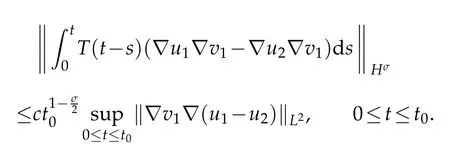
As we have done in Lemma 2.3 and 2.4,we obtain that

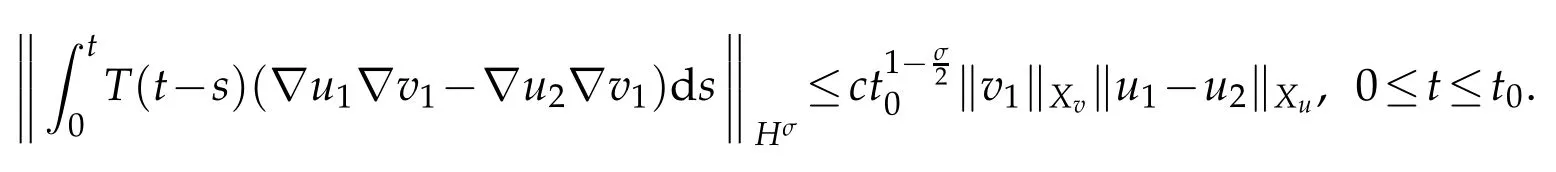
Similarly

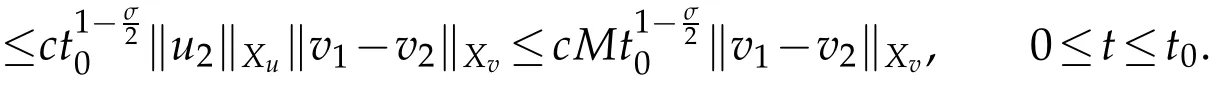
Then

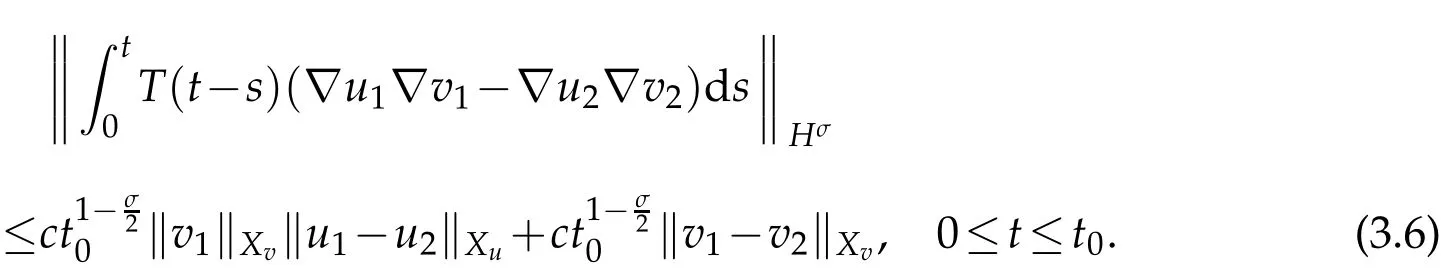
For the last term on the right side of(3.4),we have

Combining the estimates(3.5),(3.6),and(3.7),it follows that

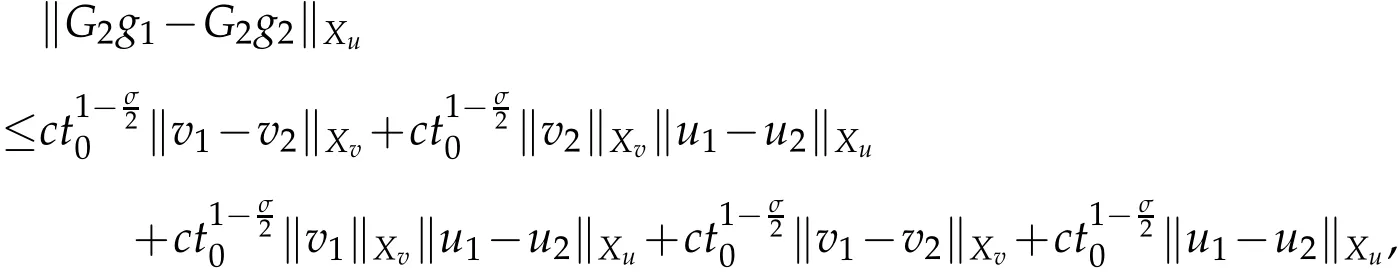
which implies

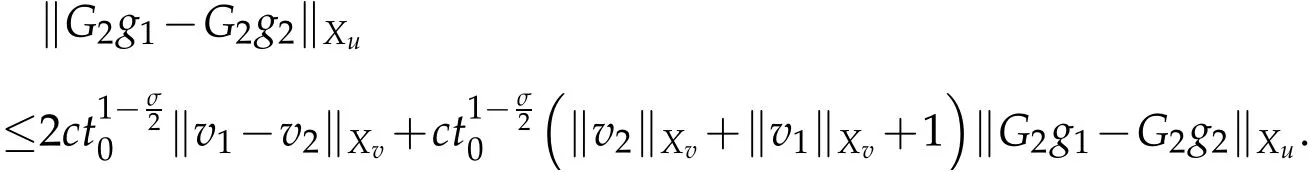
Consider the following equation

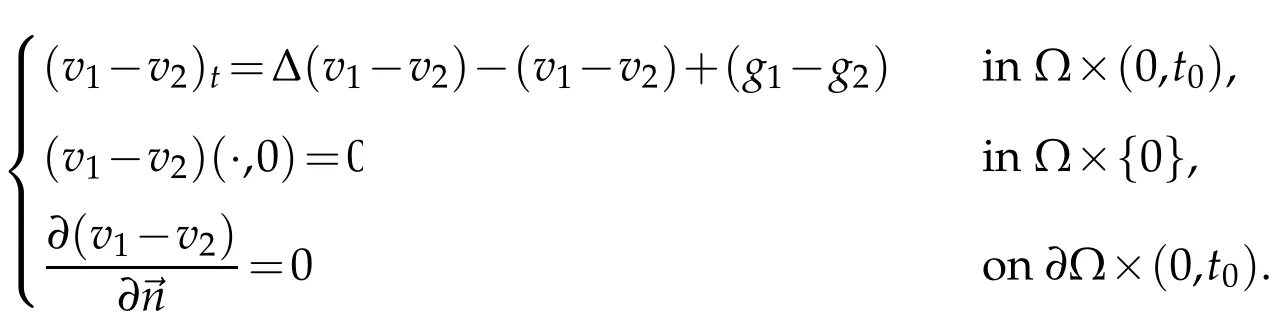
By(2.7),we obtain

Moreover,we have

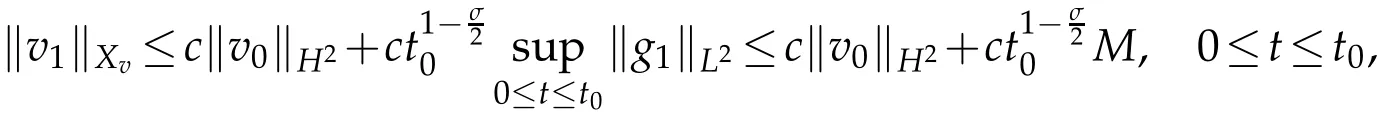
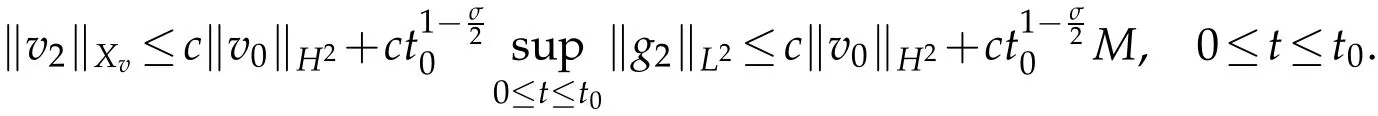
Thus fort0>0 small enough,G2is contract.

From the process above, we have proved that problem (1.1) has a solution (u,v)∈Xu×Xvby Lemmas 2.2, 2.3 and 2.4. We derive the uniqueness by Banach fixed point theorem.

4 Blow-up in finite time

We then introduce an auxiliary functionF(u)defined by

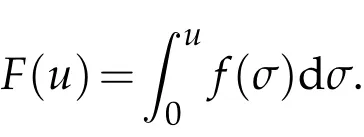
And we suppose thatN=1,then we have the following result.

Theorem 4.1.If f(u)is a convex function on[0,∞),and F(u)satisfies

then all nonnegative solutions of(1.1)blow up in finite time.

Proof.In the section,without causing any confusion,we may useCi(i=0,1,2...)to denote various positive constants.

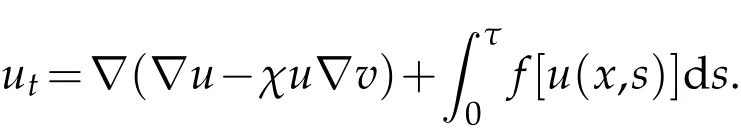
Integrate both sides of the equation on ?,

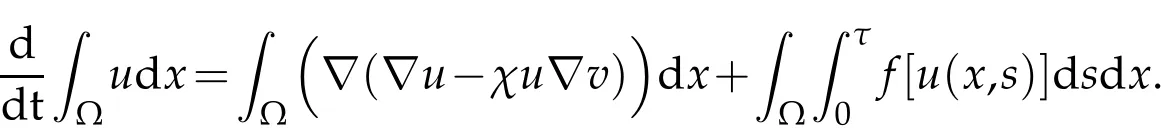
By using,we can get the following equality:

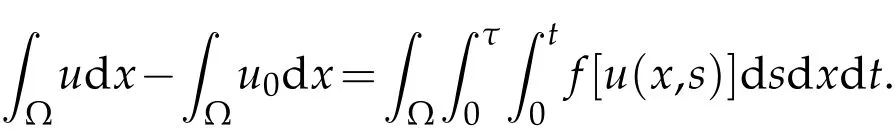
Set

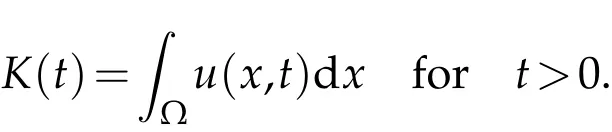
By using Jensen’s inequality,we find

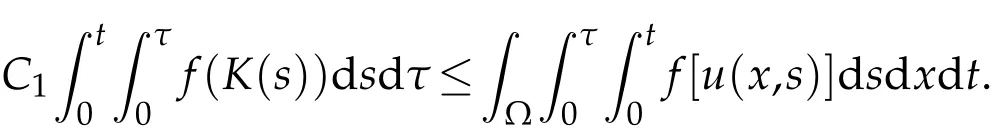
Then we can get thatK(t)satisfies

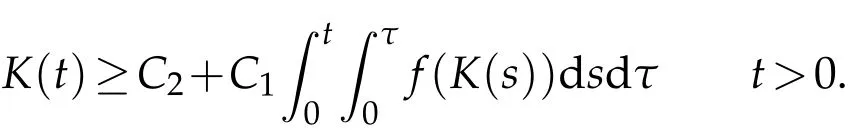
Assume to the contrary that(1.1)has a global solutionu. Then for any positive number T,we have

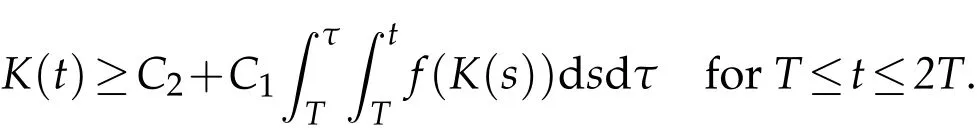
Thus,by comparision,K(t)≥k(t)on[T,2T],where

Clearly,k(t)satisfies

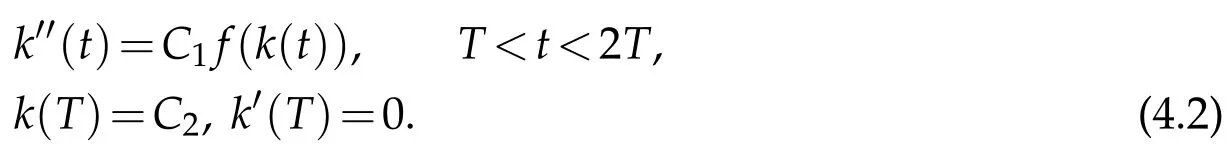
Multiplying the equation in(4.2)byk′(t)and integrating fromTtot,we obtain

Integration of this relation over(T,2T)then leads to

where c is a positive constant chosen so thatF(c)=2F(k(T))=2F(C2). For sufficiently largeT,inequality(4.3)yields a contraction to condition(4.1),which completes the proof.

Ackhowledgement

We would like to thank the referees and our advisor for carefully reading the manuscript and for their helpful suggestions.