一道北京大學自主招生試題的探究與推廣

廣東省中山紀念中學(528454) 鄧啟龍

題目(2016年北京大學自主招生) 在圓內(nèi)接四邊形ABCD中,AB= 136,BC= 80,CD= 150,DA= 102,則它的外接圓直徑為( )

分析已知圓內(nèi)接四邊形ABCD的四條邊長,如何求它的外接圓直徑? 若圓內(nèi)接四邊形ABCD形狀特殊,比如存在內(nèi)角為直角,則易求外接圓直徑.然后去尋找存在內(nèi)角為直角的條件,于是得到解法一.若不考慮圓內(nèi)接四邊形ABCD的特殊形狀,從一般情況出發(fā),結合正余弦定理,求出內(nèi)角和對角線長,然后得到外接圓直徑,于是得到解法二.

解法一由AB2+DA2= 1362+ 1022= 1702,BC2+CD2= 802+1502= 1702得A=C=,BD=170,且BD為外接圓直徑,所以外接圓直徑為170.

解法二如圖1,連接AC.由余弦定理得AC2=AB2+BC2?2AB ·BCcosB,AC2=CD2+DA2?2CD·DAcosD.由B+D=π得cosD=?cosB.所以AB2+BC2?2AB·BCcosB=CD2+DA2+2CD·DAcosB,即1362+802?2·136·80 cosB=1022+1502+2·102·150 cosB,得cosB=于是sinB=由余弦定理得AC2=AB2+BC2?2AB · BCcosB=1362+802?2·136·80·= 5184,所以AC= 72.由正弦定理得外接圓直徑2R==170.

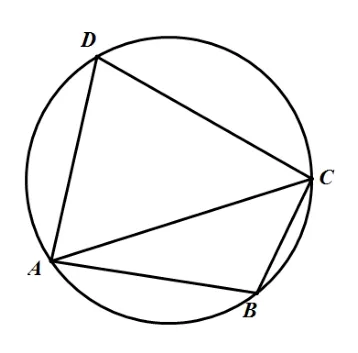
圖1

解法一只適用于存在內(nèi)角為直角的圓內(nèi)接四邊形,解法二適用于一般的圓內(nèi)接四邊形.接下來研究一般的圓內(nèi)接四邊形.

在圓內(nèi)接四邊形ABCD中,AB=a,BC=b,CD=c,DA=d,對角線AC,BD交于點E,如圖2.由余弦定理得AC2=AB2+BC2?2AB ·BCcosB,AC2=CD2+DA2?2CD·DAcosD.由B+D=π得cosD=?cosB.

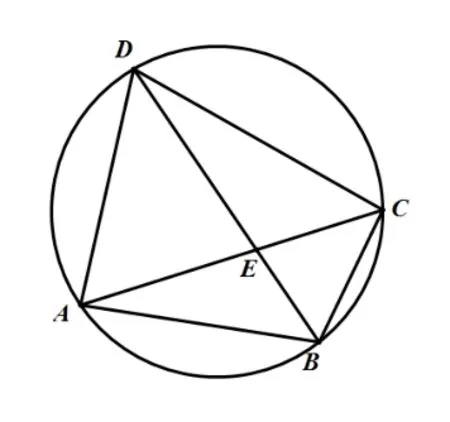
圖2

所以AB2+BC2?2AB·BCcosB=CD2+DA2+2CD·DAcosB,即a2+b2?2abcosB=c2+d2+2cdcosB,得cosB=于是

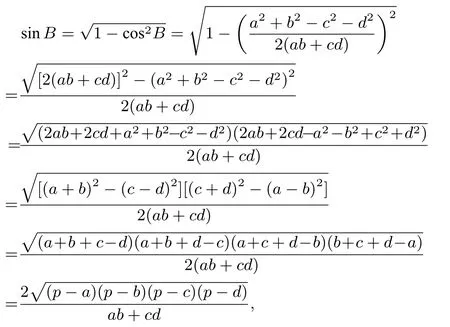
其中p=為半周長.

于是得到以下結論:

結 論1cosA=(a2+d2?b2?c2)/2(ad+bc),sinA=cosB=a2+b2?c2?d22(ab+cd),sinB=

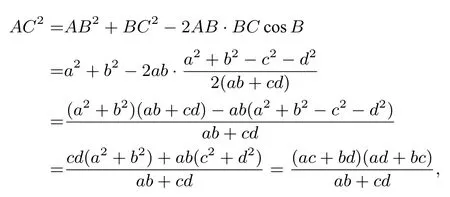
所以AC=同理可得BD=于是得到以下結論:

結論 2AC=

由結論2 得AC·BD=ac+bd=AB·CD+BC·DA,此即托勒密定理.由正弦定理和結論2 得外接圓直徑于是得到以下結論:

結論3外接圓半徑

在圓內(nèi)接四邊形ABCD中,a=AB=136,b=BC=80,c=CD= 150,d=DA= 102,則半周長p= 234,所以外接圓直徑

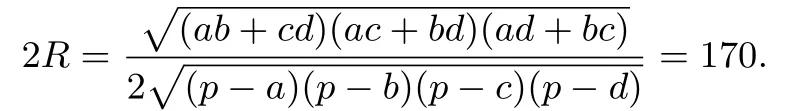
如圖2,在圓內(nèi)接四邊形ABCD中,設AE=adx,由?AEB∽?DEC得所以DE=cdx,同理可得BE=abx,CE=bcx.由AC=AE+CE=(ad+bc)x和結論2 得于是得到以下結論:

結論4

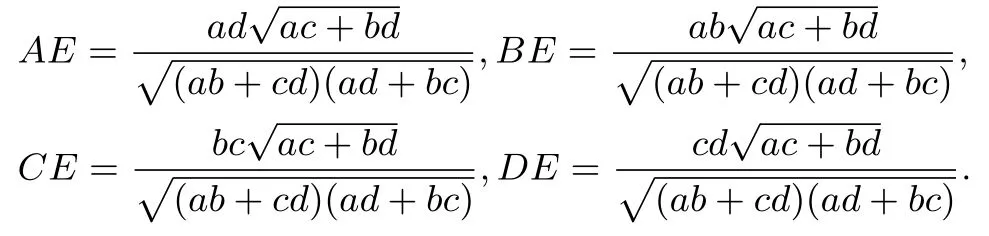
由結論1 得圓內(nèi)接四邊形ABCD的面積

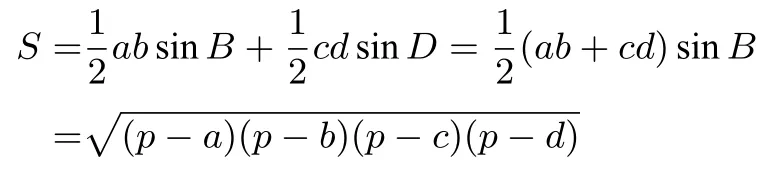
于是得到以下結論:

結論5圓內(nèi)接四邊形ABCD的面積S=若d= 0,則圓內(nèi)接四邊形ABCD退化為三角形ABC,面積S=此即海倫公式.

對于一般的平面凸四邊形(如圖3)ABCD,若AB=a,BC=b,CD=c,DA=d,如何表示它的面積?

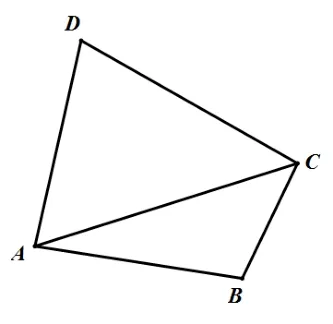
圖3

連接AC,由余弦定理得AC2=AB2+BC2?2AB·BCcosB,AC2=CD2+DA2?2CD·DAcosD.

所以AB2+BC2?2AB·BCcosB=CD2+DA2?2CD·DAcosD,即a2+b2?2abcosB=c2+d2?2cdcosD,得abcosB ?cdcosD=凸四邊形ABCD的面積sinD,于是absinB+cdsinD=2S.所以

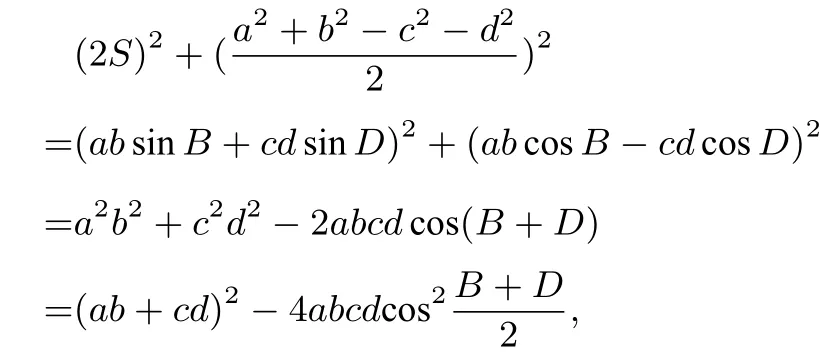
得

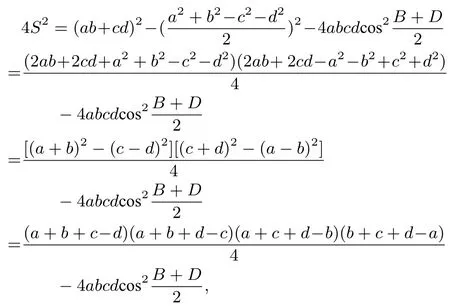
令p=為半周長,則S2=(p ?a)(p ?b)(p ?c)(p ?d)?abcdcos2于是得到以下結論:

結論6凸四邊形ABCD的面積

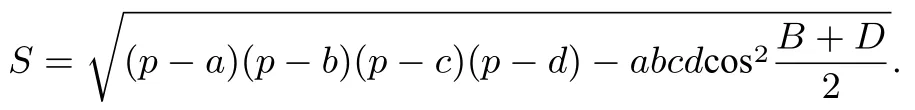
若凸四邊形ABCD為圓內(nèi)接四邊形,則B+D=π,面積S=此即結論5.

若凸四邊形ABCD為圓外切四邊形,即凸四邊形ABCD有內(nèi)切圓,則p=a+c=b+d,面積S=

若凸四邊形ABCD既是圓內(nèi)接四邊形,又是圓外切四邊形,即凸四邊形ABCD既有外接圓,又有內(nèi)切圓,則面積